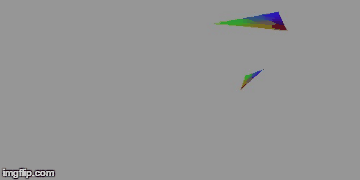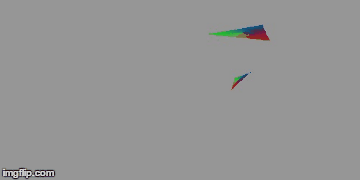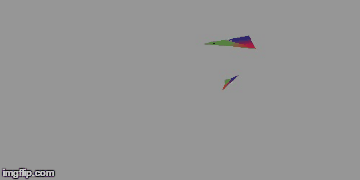Algorithme de rendu de scène 3D par Z-buffer
Un algorithme de rendu de scène 3D est un procédé permettant de passer d’une scène en trois dimensions à une projection de cette scène sur un écran en deux dimensions afin de pouvoir la visualiser.
Une scène est un environnement (monde) comportant des objets (cube, sol, lumière…). Le rendu de cette scène est une image en 2D de cette dernière par rapport à un point de vue (caméra).
Dans la vie réelle l’environnement pourrait être une salle de classe et les objets des chaises, des tables ou encore des néons. L’image de cette salle serait alors celle interprétée par notre œil (notre point de vue) et plus précisément celle formée par les rayons lumineux sur notre rétine.
Afin de garder l’effet de profondeur il faut appliquer lors du rendu un Z-buffer (tampon de profondeur) afin de définir les surfaces cachées par les objets sur le plan de devant.
Les algorithmes principaux
Il existe deux algorithmes principaux pour le rendu de scène 3D, chacun utilisés pour des besoins spécifiques.
Le lancer de rayon (ray-tracing)
Cette méthode de rendu est dite centrée image du fait que les rayons sont tirés de la caméra (image) vers la scène. Elle permet de gérer plusieurs phénomènes optiques tel que la réflexion, la réfraction ou encore la transparence. Cette méthode est donc utilisée pour un rendu réaliste et proche de la réalité si bien qu’elle nécessite beaucoup de ressources pour fonctionner.
La rastérisation
Cette deuxième méthode est dite centrée objet, c’est-à-dire à l’inverse de la précédente, ce sont les objets qui sont projeté vers la caméra. Cet algorithme de rendu de scène 3D permet de gérer des ombres (shadow map), des lumières (light map) et des reliefs (bump map). L’avantage de cette méthode est qu’elle se base sur des procédures simples et rapides et permet donc de faire du rendu en temps réel (en général 24 images/seconde). C’est donc cette méthode (avec quelques variantes) qui est implémentée sur les cartes graphiques et permet entre autres le fonctionnement des jeux vidéo.
Rastérisation : La projection
La scène à différentes échelles
La scène (ou l’environnement) est composée d’objets simples ou complexes (cubes, sphères, personnages…). En excluant des cas spéciaux comme les caméras et les lumières, ces objets sont eux-mêmes composés de formes simples tel que des polygones et plus généralement, des triangles. La plus petite échelle d’une scène se rapporte aux sommets (vertices) délimitant ces formes simples, par exemples, les trois sommets d’un triangle. Il faut savoir que pour chaque échelle le système de coordonnées diffère, en effet les sommets sont placés par rapport au repère de la forme, la forme au repère de l’objet et enfin l’objet par rapport au repère de la scène.
Le principe
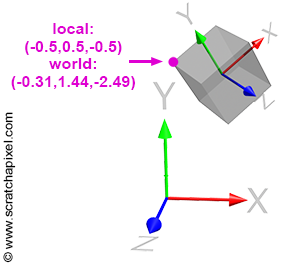
De manière plus générale notre point dit local (celui placé par rapport à la forme) doit être envoyé dans le monde et donc posséder de nouvelles coordonnées. Une fois dans le monde le point doit être positionné par rapport au repère de la caméra afin de pouvoir être projeté sur l’écran fictif de cette dernière pour enfin êtres positionné par rapport à l’écran de l’utilisateur (ou canevas).
Pour passer de repère en repère il faut utiliser des matrices, voici les trois utilisés :
- La matrice transformation (T), permettant de passer des coordonnées locales aux coordonnées dans le monde (l’environnement).
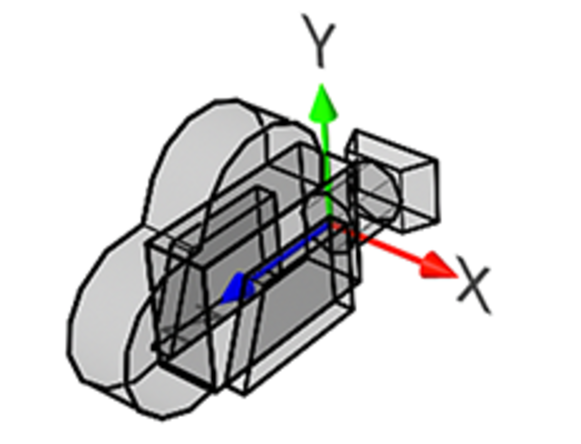
- La matrice visualisation (V), permettant de passer des coordonnées de l’objet par rapport au monde à celles de l’objet par rapport à la caméra.
- La matrice perspective (P), qui permet de « projeter » les coordonnées caméra vers l’écran.
Voici l’équation finale de la transformation locale vers écran :
Il faut noter qu’une fois les coordonnées définies sur l’écran il faut faire une mise à l’échelle par rapport à la taille du canevas, ceci en passant par un système de coordonnées spécifique, le NDC (Normalized Device Coordinates).
Local vers monde : La matrice Transformation
Cette matrice est composée elle-même de trois autres matrices qui une fois multipliées entre elles, forment la matrice Transformation.
Ces trois matrices sont :
- La matrice dilatation
- La matrice rotation
- La matrice translation
Au final on a :
La matrice dilatation
Pour effectuer un étirement sur un objet il faut tout d’abord comprendre le principe de la matrice identité.
C’est une matrice carrée (autant de ligne que de colonne) et sa diagonale est composée de 1, le reste de 0. Voici la matrice en question :
Sa particularité est que toute matrice multipliée par celle-ci restera inchangée (du moment que leur taille est compatible).
Exemple :
C’est le principe simple de cette matrice qui nous permet de créer la matrice de dilatation.
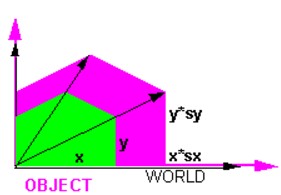
Cette matrice comme son nom l’indique va permette de modifier l’échelle de taille de l’objet par rapport aux axes x,y et z.
La diagonale est composée des coefficients de dilatation sur ces trois axes. Ces coefficients peuvent aussi bien être positifs que négatifs.
Voici la formule générale :
Exemple :
La matrice rotation
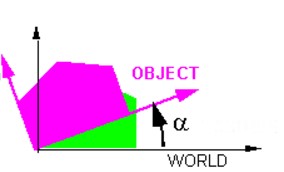
Pour faire tourner un objet autour d’un axe du repère cartésien il faut utiliser les fonctions trigonométriques.
Exemple pour faire tourner un objet autour de l’axe x, la valeur en x ne change pas :
Lorsque aucune rotation n’est appliquée il faut trouver une fonction qui retourne la valeur de la matrice identité lorsque .
Ici il faut utiliser :
Échec de l’analyse (erreur de syntaxe): {\displaystyle \cos 0=1}
Échec de l’analyse (erreur de syntaxe): {\displaystyle \sin 0=0}
La matrice obtenue pour l’axe x est donc :
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \begin{pmatrix}1&0&0\\0&\cos\theta&\sin\theta\\0&-\sin\theta&\cos\theta\end{pmatrix}}
Le signe "–" sert à garder l’orthogonalité du repère lors d'une rotation horaire (non-trigonométrique) :
Voici la matrice de rotation pour chaque axe :
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle r.x = \begin{pmatrix}1&0&0\\0&\cos\theta&\sin\theta\\0&-\sin\theta&\cos\theta\end{pmatrix}}
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle r.y = \begin{pmatrix}\cos\theta&0&-\sin\theta\\0&1&0\\ \sin\theta&0&\cos\theta\end{pmatrix}}
Échec de l’analyse (fonction inconnue « \begin{pmatrix} »): {\displaystyle r.z = \begin{pmatrix}\cos\theta&\sin\theta&0\\-\sin\theta&\cos\theta&0\\0&0&1\end{pmatrix}}
Pour tourner autour de plusieurs axes à la fois il suffit de multiplier les coordonnées avec les matrices des axes en question :
La matrice translation
Pour appliquer une translation à un point, il faut simplement ajouter une valeur T (positive ou négative) correspondant au « déplacement » du point sur un axe. Voici la démonstration qui résume cette démarche avec des matrices :
Qui peut s’écrire :
Pour réaliser cela il faut ajouter une 4ieme composante aux coordonnées du point P, ces dernières seront donc d’après l’équation :
La matrice de transformation aura la forme :
Il faut noter que la dernière colonne de cette matrice sera toujours la même (en effet s’il on change ces valeurs le point aura une coordonnée du type . Certes il existe des utilisations de cette dernière colonne mais elles ne seront pas abordées.
Le point finalement obtenu aura pour coordonnées :
Finalement, la matrice globale, regroupant ces trois « sous »-matrices est définie par :
Échec de l’analyse (fonction inconnue « \begin{pmatrix} »): {\displaystyle T = \begin{pmatrix} \lambda_1 & 0 & 0 & 1\\0 & \lambda_2 & 0 & 1\\ 0 & 0 & \lambda_3 & 1\end{pmatrix} \times \begin{pmatrix}1&0&0 & 1\\0&\cos\theta&\sin\theta & 1\\0&-\sin\theta&\cos\theta & 1\end{pmatrix} \times \begin{pmatrix}\cos\theta&0&-\sin\theta & 1\\0&1&0 & 1\\ \sin\theta&0&\cos\theta & 1\end{pmatrix} \times \begin{pmatrix}\cos\theta&\sin\theta&0 & 1\\-\sin\theta&\cos\theta&0 & 1\\0&0&1 & 1\end{pmatrix} \times \begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\Tx&Ty&Tz&1\end{pmatrix}}
Ou encore :
Monde vers caméra : La matrice Visualisation
Il faut tout d’abord comprendre que la caméra peut être considérée comme un objet, elle dispose donc de sa propre matrice de transformation pour se placer dans le monde. Cette matrice est définie par la matrice V.
Afin de placer les coordonnées du monde par rapport à la caméra il suffit de les multiplier par la matrice inverse de la matrice transformation de la caméra.
La matrice permet de placer les points, au départ du monde, par rapport au repère de la caméra.
Caméra vers écran : La matrice perspective
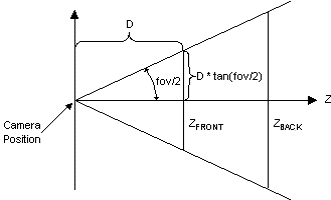
Afin de projeter les points sur une surface tel que l’écran il faut utiliser le théorème de Thalès (voir image). Il faut bien-sûr prendre en compte le champ de vision de la caméra (fov) ainsi que la distance du premier plan et de l’arrière-plan afin de construire le triangle de référence aussi appelé tronc de visualisation (viewing frustum).
La surface visible est définie grâce au fov avec la formule suivante :
Échec de l’analyse (erreur de syntaxe): {\displaystyle S=\frac{1}{tan(\frac{fov}{2}*\frac{\pi}{180})}}
Ce qui donne finalement la matrice P :
Ici, f et n correspondent respectivement à la distance avec le plan lointain (far) et le plan proche (near).
A partir de maintenant le travail se fait de nouveau sur des coordonnées (x,y,z).
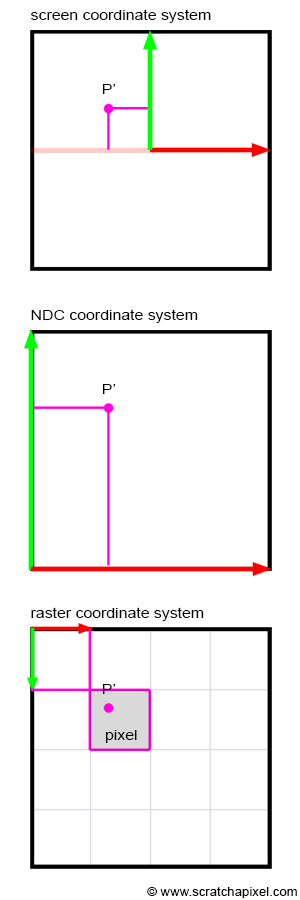
Ecran vers raster : Mise à l’échelle
Pour passer des coordonnées sur l’écran vers la grille de pixel (raster ou canevas) que compose un écran d’ordinateur il faut d’abord passer par un système de coordonnées normalisé que l’on appel plus souvent NDC (pour Normalized Device Coordinate). Ce système permet de passer des coordonnées dans à des coordonnées entre 0 et 1. Pour cela il faut modifier les coordonnées par :
Ici les valeurs de sont entre 0 et 1, largeur et hauteur se rapportent aux dimensions de l’image.
Finalement pour placer ces nouveaux points sur notre espace rastérisé (canevas ou grille de pixels) il faut multiplier par la largeur et par la hauteur de l’image et utiliser l’arrondi à l’entier inférieur ou égal (floor). Il faut penser à prendre en compte que l’espace rastérisé est inversé sur l’axe y ce qui nous donne :
Le cheminement de la coordonnée locale à la coordonnée rastérisée est donc terminé et les points obtenus sont exploitables pour la partie suivante qu’est la visualisation de la scène.
Rastérisation - Visualisation
Dans cette partie il sera question de triangles qui est la forme la plus simple pour former des objets complexes et qui est utilisée sur une CG (carte graphique).
Trouver les pixels contenus dans le triangle
Juan Pineda
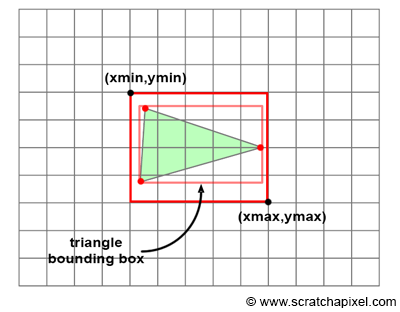
Afin de trouver quels pixels sont contenus dans le triangle formé par trois points projetés sur l’espace rastérisé il faut tout d’abord réduire la zone de tests de pixels au maximum.
Pour cela il faut définir une boite de délimitation (bounding box) qui n’est ni plus ni moins que le plus petit rectangle pouvant encadrer le triangle.
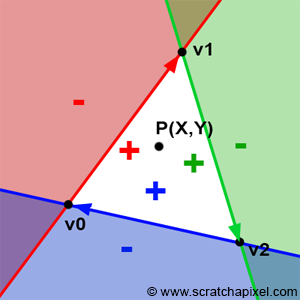
Ensuite il faut mettre en place la fonction des bords (edge function : Juan Pineda). Cette fonction calcule le déterminant entre un point de la boite et la droite définissant un bord du triangle. Si pour les trois bords le déterminant est positif alors le point est à l’intérieur du triangle. Il faut cependant définir au départ un sens de rotation en définissant un index pour chaque sommet du triangle afin que le côté de la droite positif corresponde bien à l’intérieur du triangle. Voici la formule du déterminant :
Si Alors le point est à l’intérieur du triangle, sinon il est à l’extérieur
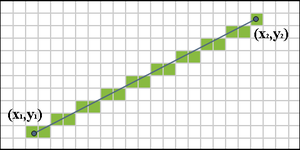
Jack E. Bresenham
Il existe une alternative à cette méthode qui est l’algorithme de Bresenham. Cet algorithme retourne la liste des pixels compris sur la droite reliant deux pixels. Grâce aux listes obtenues il est possible de faire « boucler » notre algorithme entre chaque ligne ce qui réduit de façon non négligeable les pixels traités dans le cas de grands triangles. Au départ il faut définir le point le plus haut puis à partir de ce point définir le segment le plus court pour relier un des deux autres points. Enfin une fois le premier segment parcouru en entier il faut créer un segment du sommet contenu par le segment court jusqu’au point final (contenu par le segment le plus long). En définissant quel segment est à gauche (ou droite) il est possible de définir les bornes de la boucle et ainsi de retirer la liste des pixels contenu dans le triangle.
Par rapport à la méthode précédente l'avantage est de ne pas avoir à tester des pixels hors triangle ainsi que de ne pas avoir à préciser d'index.
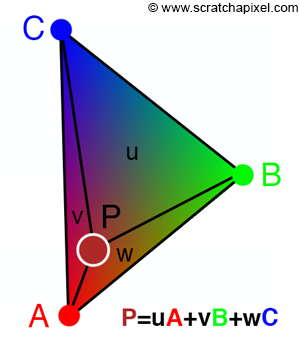
Une fois les pixels contenus trouvés il faut colorier le triangle sans avoir à donner une couleur à chaque pixel. Pour cela l’utilisation des coordonnées barycentrique est requise.
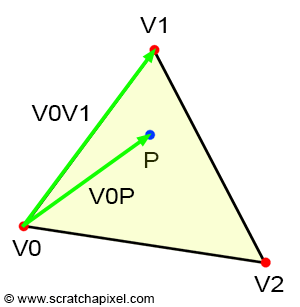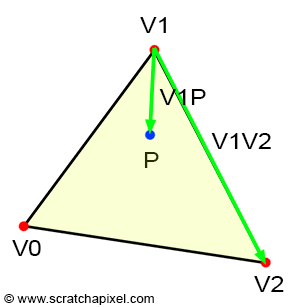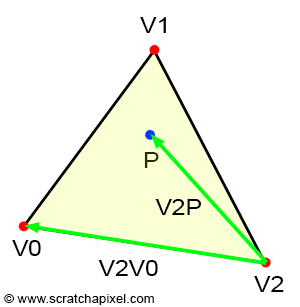
Les coordonnées barycentriques
Ce sont trois coefficients, un par axe permettant de localiser un point quelconque du triangle par rapport au trois sommets. Encore une fois l’utilisation du déterminant permet de définir ces trois coefficients. Tout d’abord il faut définir trois triangles par rapport au point P compris dans le triangle. Ensuite, le premier coefficient est défini par l’aire du premier sous-triangle divisé par l’aire du triangle complet et ainsi de suite pour chaque coefficient. Les formules obtenues :
La coloration par interpolation
Pour colorier chaque pixel du triangle il faut utiliser les coordonnées barycentriques définies précédemment. En effet la couleur d’un pixel par rapport aux couleurs des trois sommets est donnée par :
Il faut ici noter que la couleur est au format RGB (rouge, vert, bleu).
C’est ainsi qu’un pixel est colorié sans lui donner une couleur manuellement.
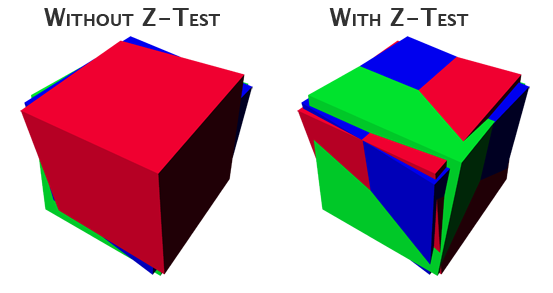
L’implémentation du Z-buffer
Dans le cas où plusieurs objets sont présents sur la scène il est probable que par rapport au point de vue certains soit devant d’autres et ainsi les cache visuellement parlant. Pour éviter une superposition dans l’ordre de rendu des surfaces un tampon de profondeur (ou Z-buffer, z car par rapport à l’axe de la profondeur) est utilisé. Le Z-buffer garde en mémoire la composante z la plus proche de la caméra obtenue. Ainsi avec une initialisation à moins l’infinie () il est possible de comparer chaque profondeur de chaque point avec l’ancienne et ainsi voir si le pixel est visible ou caché par un autre.
Encore une fois on utilise les coordonnées barycentriques pour définir la profondeur de chaque pixels du triangle sans avoir à les indiquer manuellement.
On utilise la formule :
C’est entre autres avec ce Z-buffer que l’on peut être en mesure de calculer des ombres.
Le rendu de la scène
A ce stade une liste de points et une couleur associée à chacun est obtenue, il est donc possible de créer une image de la scène.
Cela est simple, il faut commencer par une initialisation de l’image à la taille demandée (largeur, hauteur). Ensuite il faut définir un fichier de sortie puis parcourir la liste afin de colorier les pixels présents dans la liste. Le plus simple pour effectuer cela est d’utiliser le format d’image PPM (P3) afin de bénéficier d’une écriture simple.
Voici quelques exemples de rendu :
Algorithme final Python
Voici le code Python en lien avec le sujet. Pour pouvoir l’exécuter il faut utiliser la bibliothèque NumPy ainsi que la bibliothèque image. Les liens sont en annexe, pour ma part, j'ai utilisé Jupyter notebook et Anaconda pour faire fonctionner les bibliothèques.
# coding: utf-8
#Importations necessaires
import numpy as np
from numpy.linalg import inv
from math import cos, sin, tan, pi, floor, inf
from image import Image #Importation bibliothèque image (TP1-Math202)
# 1. Projection
# Fonctions transformation dans le monde
def dilatation(v, Cx, Cy, Cz):
"""
Cx, Cy, Cz les coefficients de dilatation par axe
v : les coordonnées x,y,z du point
"""
#Multiplication avec numpy (.dot(a,b))
return np.dot(v, [[Cx,0,0],[0,Cy,0],[0,0,Cz]])
def rotation(v, axe, angle):
"""
v = [x,y,z] tab
axe = "x", "y" ou "z" str
angle = float en degré
"""
a = (angle*pi)/180 #Passage de l'angle en radian
c = cos(a)
s = sin(a)
#Test pour trouver la bonne matrice de rotation
if axe == "x":
m_rotation = [[1,0,0],[0,c,-s],[0,s,c]]
elif axe == "y":
m_rotation = [[c,0,s],[0,1,0],[-s,0,c]]
elif axe == "z":
m_rotation = [[c,-s,0],[s,c,0],[0,0,1]]
else:
print("Erreur axe: 'x', 'y' ou 'z'")
m_rotation = [[1,0,0],[0,1,0],[0,0,1]]
return np.dot(v, m_rotation)
def translation(v, Tx, Ty, Tz):
"""
v = [x,y,z,1]
Tx, Ty, Tz = entier
"""
#Si la coordonnée est toujours de taille 1*3 et non 1*4
if len(v) != 4:
return print("Erreur: v = [x,y,z,1]")
return np.dot(v, [[1,0,0,0],[0,1,0,0],[0,0,1,0],[Tx,Ty,Tz,1]])
def matrice_T(d, r, t):
"""
d = [dx,dy,dz] Les coefficients de dilatation sur chaque axe
r = [ax,ay,az] Les angles de rotation autour de chaque axe
t = [tx,ty,tz] Les coefficients de translation sur chaque axe
"""
tra = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[t[0],t[1],t[2],1]] #Matrice translation
dil = [[d[0],0,0,0],[0,d[1],0,0],[0,0,d[2],0],[0,0,0,1]] #Matrice dilatation
a = (r[0]*pi)/180
c = cos(a)
s = sin(a)
Rx = [[1,0,0,0],[0,c,-s,0],[0,s,c,0],[0,0,0,1]]
a = (r[1]*pi)/180
c = cos(a)
s = sin(a)
Ry = [[c,0,s,0],[0,1,0,0],[-s,0,c,0],[0,0,0,1]]
a = (r[2]*pi)/180
c = cos(a)
s = sin(a)
Rz = [[c,-s,0,0],[s,c,0,0],[0,0,1,0],[0,0,0,1]]
rot = np.dot(Rx,Ry)
rot = np.dot(rot, Rz) #Matrice rotation
#Multiplication des trois sous-matrices
T = np.dot(dil, rot)
T = np.dot(T, tra)
return T
#Fonction local vers monde n'utilisant pas la fonction Matrice_T afin
#d'illustrer le fonctionnement
def local_vers_monde_v1(v, d, r, t):
"""
v = [x,y,z] Les coordonnées de base du point
d = [dx,dy,dz] Les coefficients de dilatation sur chaque axe
r = [ax,ay,az] Les angles de rotation autour de chaque axe
t = [tx,ty,tz] Les coefficients de translation sur chaque axe
"""
v_proj = dilatation(v,d[0],d[1],d[2])
tab = ["x","y","z"]
for i in range(3):
v_proj = rotation(v_proj, tab[i], r[i])
v_proj = np.insert(v_proj,v_proj.size,1)
point_monde = translation(v_proj, t[0], t[1], t[2])
return point_monde
# Procedure détaillée de la projection
#Fonction local vers monde utilisant fonction Matrice_T
#plus pertinante
def local_vers_monde(point, d, r, t):
"""
point = [x,y,z,1] Les coordonnées de base du point
d = [dx,dy,dz] Les coefficients de dilatation sur chaque axe
r = [ax,ay,az] Les angles de rotation autour de chaque axe
t = [tx,ty,tz] Les coefficients de translation sur chaque axe
"""
#Deduction de la matrice transformation
T = matrice_T(d, r, t)
#multiplication
point_monde = np.dot(point,T)
return point_monde
def monde_vers_camera(point,dc,tc,rc):
"""
Projection du point dans le monde vers la camera
"""
#Projection camera dans monde puis monde dans camera
camera_monde = matrice_T([1,1,1], tc, rc) #V
camera_local = inv(camera_monde) #V^-1
#Projection du point dans l'espace camera
point_camera = np.dot(camera_local,point)
return point_camera
def matrice_P(fov, n, f):
"""
Calcul de la matrice perspective tel que vu dans le wiki
fov : champ de vision en degré
n : distance premier plan
f : distance arriere plan
"""
s = 1/(tan((fov/2)*(pi/180)))
return [[s,0,0,0],[0,s,0,0],[0,0,-f/(f-n),-(f*n)/(f-n)],[0,0,0,-1]]
def camera_vers_ecran(point,fov,proche,lointain):
"""
Projection du point sur l'ecran de la camera
"""
#Creation de la matrice perspective
perspective = matrice_P(fov, proche, lointain)
#Projection du point sur l'ecran
point_ecran = np.dot(point,perspective)
return point_ecran[:-1] #[:-1] car l'on peut desormait travaiiler sur (x,y,z)
# et non (x,y,z,1)
def ecran_vers_normalise(point, largeur, hauteur):
"""
Transformation du point aux coordonnees normalisees
"""
p = point
l = largeur
h = hauteur
#Si le point est comprit dans l'image
if (abs(p[0]) <= l/2) or (abs(p[1]) <= h/2):
#Transformation normalisée (NDC space)
p[0] = (p[0]+l/2)/l
p[1] = (p[1]+h/2)/h
return p
return None
def normalise_vers_grille(point, l, h):
"""
Transformation du point aux coordonnees pixel
"""
p = point
p[0] = floor(p[0]*l)
p[1] = floor((1-p[1])*h)
return p
# Resultat final
def procedure_local_grille(point_local,index,couleur,dp,rp,tp,dc,rc,tc,fov,proche,lointain,largeur,hauteur):
"""
Transformation totale du point local vers l'espace raster
"""
point_monde = local_vers_monde(point_local,dp,rp,tp)
point_camera = monde_vers_camera(point_monde,dc,rc,tc)
point_ecran = camera_vers_ecran(point_camera,fov,proche,lointain)
point_normalise = ecran_vers_normalise(point_ecran, largeur, hauteur)
point_grille = normalise_vers_grille(point_normalise, largeur, hauteur)
x = point_grille[0]
y = point_grille[1]
coords = (int(x),int(y),point_grille[2])
return (coords,index,couleur) #Ajout d'un index et de la couleur necessaire
#à la visualisation
# 2. Visualisation
# Recupération des coordonnées comprisent dans un triangle
def ordre(s1,s2,s3):
"""
Retourne l'ordre des sommets grace à leur index
s = ((x,y,z),i)
"""
tuples = [s1,s2,s3]
return sorted(tuples, key=lambda tuples: tuples[1])
def boite(s1,s2,s3):
"""
Génération de la plus petite boite englobant le triangle
"""
boite_start = (min(s1[0],s2[0],s3[0]),min(s1[1],s2[1],s3[1]))
boite_end = (max(s1[0],s2[0],s3[0]),max(s1[1],s2[1],s3[1]))
return (boite_start,boite_end) #(xmin,ymin),(xmax,ymax)
def interieur_bordure(s1,s2,pixel):
"""
Calcul le déterminant D pour ensuite tester si le pixel est dans le triangle
"""
return ((pixel[0] - s2[0]) * (s1[1] - s2[1]) - (pixel[1] - s2[1]) * (s1[0] - s2[0]))
def liste_pixels_coeffs(s1,s2,s3):
"""
Retourne la listes des pixels dans le triangle ainsi que leurs coefficients
par rapport à chaque sommets
"""
b = boite(s1,s2,s3)
points = []
coeffs = []
#Aire du triangle complet
aire = interieur_bordure(s1,s2,s3)
#Parcours de la bounding box
for i in range(b[0][0],b[1][0]+1):
for j in range(b[0][1],b[1][1]+1):
#Calcul des sous-aires
aire3 = interieur_bordure(s1,s2,(i,j))
aire1 = interieur_bordure(s2,s3,(i,j))
aire2 = interieur_bordure(s3,s1,(i,j))
#Si le pixel est à l'interieur des trois bords du triangle
if aire1 >= 0 and aire2 >= 0 and aire3 >= 0:
#Coordonnées barycentriques
coeff = ((aire1/aire,aire2/aire,aire3/aire))
#Calcul de la profondeur par rapport aux coords barycentriques
z = coeff[0]*s1[2]+coeff[1]*s2[2]+coeff[2]*s3[2]
points.append((i,j,z))
coeffs.append(coeff)
return (points,coeffs)
def calculer_rgb(c1,c2,c3,liste):
"""
Calcul de la couleur du pixel
"""
#Liste des points du triangle et de leur coeff
finale = liste[0]
k = 0
for i in liste[1]:
cf1 = i[0]
cf2 = i[1]
cf3 = i[2]
couleur = ()
#Pour chaque composante (r, g et b)
for j in range(3):
#Nouvelle couleur
c = floor(cf1*c1[j]+cf2*c2[j]+cf3*c3[j])
couleur += (c,)
#Correspondance du point et de la couleur (ecrase les coord barycentriques)
finale[k] = (finale[k],couleur)
k += 1
return finale
def remplir(s1,s2,s3):
"""
Renvoie la liste des pixels ainsi que leur couleur
s = ((x,y,z),i,(r,g,b))
"""
o = ordre(s1,s2,s3)
liste = liste_pixels_coeffs(o[0][0],o[1][0],o[2][0])
return calculer_rgb(s1[2],s2[2],s3[2],liste)
# Image
def creer_image(l,h,fond,fichier):
"""
Création d'une image vierge
l = largeur
h = hauteur
fichier = fichier de sortie
fond = couleur du fond (r,g,b)
"""
#ouverture du fichier en mode lecture
image = open(fichier,"w")
image.write("P3\n"+str(l)+" "+str(h)+"\n255\n")
#Mettre tous les pixels à la couleur du fond
for i in range(h):
for j in range(l):
image.write(str(fond[0])+" "+str(fond[1])+" "+str(fond[2])+"\n")
#fermeture du fichier
image.close()
return None
def rendu(liste,fichier):
"""
Ecrit les nouveaux pixel sur l'image
"""
im = Image(fichier)
for i in liste:
x = i[0][0]
y = i[0][1]
c = i[1]
#Mise à jour des nouveaux pixels avec leur couleur
im.setPixel(x,y,c)
im.save(fichier)
return None
def rendu_total(l,h,fond,fichier,liste):
"""
Créé l'image en partant des dimensions et de la liste de pixels
"""
creer_image(l,h,fond,fichier)
rendu(liste,fichier)
return None
# Implementation du z-buffer
def initialisation_z_buffer(l,h):
"""
Creation d'un tableau 2D avec chaque case = -inf
"""
z_buffer = []
#Ligne
for i in range(0,h):
z_buffer.append([])
for j in range(0,l):
z_buffer[i].append(-inf)
return z_buffer
def cache(z_buffer,p):
"""
Test si un pixel est cache
"""
if p[2] <= z_buffer[p[1]][p[0]]:
return True
return False
def modifier_z_buffer(z_buffer,p):
"""
Modifie la case avec la nouvelle profondeur
"""
z_buffer[p[1]][p[0]] = p[2]
return z_buffer
def rendu_z_buffer(liste,fichier,z_buffer):
"""
Rendu de l'image en prenant compte le z-buffer
"""
#Ouverture de l'image
im = Image(fichier)
for i in liste:
x = i[0][0]
y = i[0][1]
z = i[0][2]
c = i[1]
#tests z-buffer
if not cache(z_buffer,(x,y,z)):
z_buffer = modifier_z_buffer(z_buffer,(x,y,z))
im.setPixel(x,y,c)
#Sauvegarde de l'image
im.save(fichier)
return None
# Algorithme final
def rasterisation(triangles,c,image):
"""
triangles : [[[[(x,y,z),index,couleur],[(x,y,z),index,couleur],[(x,y,z),index,couleur]],dp,rp,tp],triangle2...]
c (camera) : [dc,rc,tc,fov,proche,lointain]
image : [largeur,hauteur,fond,fichier_sortie]
"""
points_p = []
triangles_p = []
l = image[0]
h = image[1]
fond = image[2]
fichier = image[3]
#Pour chaque triangle
for t in triangles:
#Pour chaque point
for p in t[0]:
point = p[0]+(1,)
points_p.append(procedure_local_grille(point,p[1],p[2],t[1],t[2],t[3],c[0],c[1],c[2],c[3],c[4],c[5],l,h))
#Ajout du nouveau point
triangles_p.extend([points_p])
points_p = []
liste_pixels_t = []
#Pour chaque triangle projete
for t in triangles_p:
liste_pixels_t.append(remplir(t[0],t[1],t[2]))
#Initialisation z-buffer global car reutilise dans plusieurs fonctions
global z_buffer
z_buffer = initialisation_z_buffer(l,h)
creer_image(l,h,fond,fichier)
#Test z-buffer
for p in liste_pixels_t:
rendu_z_buffer(p,fichier,z_buffer)
return ("Rendu terminé")
Le fichier donné en annexe comporte des exemples ainsi que l'algorithme de Bresenham.
Sources
Scratch a pixel
Wikipédia :
Lama :
Annexes
Python :
- Bibliothèque Image (ou ici) à placer dans le même dossier que l'algorithme Python.
- Algorithme Python
IDLE avec NumPy :
- Anaconda Installez Anaconda puis ouvrez Anaconda Prompt et tapez :
jupyter notebook
Autres :
Auteur : Tournafond Raphaël, L1, CMI-INFO