Algorithmes probabilistes/déterministes pour tester la primalité d'un entier

L'objectif de ce projet était de comprendre les différences entre des tests de probabilité. En effet, il existe différents types de tests, les probabilistes et déterministes. Le but de ces tests est de déterminer le plus rapidement possible et de la façon la plus sûre possible, si un nombre est premier ou non.

La primalité d'un entier

Un entier est dit premier s'il est seulement divisible par 1 et lui même.

Algorithmes

Probabiliste

Un algorithme probabiliste utilise une source de hasard. Son déroulement fait appel à des données qui sont tirées au hasard. Il est généralement plus simple à analyser et beaucoup plus rapide à l'exécution.

Déterministe

Etant donné une entrée particulière, un algorithme déterministe donnera toujours la même sortie. La machine sous-jacente passera toujours par la même séquence d'état. L'algorithme déterministe est en fait le contraire de l'algorithme probabiliste. Il n'utilise pas d'état externe (par exemple une variable aléatoire).

Le Crible d’Ératosthène

Son fonctionnement

Le Crible d’Ératosthène est un test de primalité des entiers déterministe. Il permet donc de vérifier si un entier N est premier. Il utilise une variable (notée D) allant de 2 jusqu'à ${\sqrt {N}}$ et vérifie la condition suivante: Tant que N est n'est pas divisible par D, on augmente la valeur de D. Ainsi, si jamais on tombe sur une valeur de D telle que N est divisible par D alors on peut dire que N est composé. Si N n'est divisible par aucune valeur de D, alors N est premier.

Programmation en python

def eratosthene(n):

   """en entree : n l'entier a tester
   en sortie: un booleen (True si premier) """
   d=2
   r=n%d
   if r == 0:
       return False
   d=3
   while d<= sqrt(n):
       r=n%d
       if r ==0:
           return False
       d+=2
   return True

Le test de Fermat

Son fonctionnement

Le test de primalité de Fermat est un test probabiliste. Il utilise une variable K qui permet de déterminer le nombre de fois que l'on va effectuer le test.

Deux versions différentes

La version dite faible

Si p premier ; Alors $a^{p}-a$ est divisible par p

La version dite Forte

Si p premier ; si a et p premier entre eux ; Alors $-1+a^{p-1}$ est divisible par p

Programmation en python

def fermat(n, k):

   """ en entree: n un entier et k un entier positif choisi
       en sortie: un booleen"""
   res=True
   for _ in range(k):
       a = randrange(2,n-1)
       if pow(a,k,n-1)!= 1:
           res = False
   return res

Les valeurs des puissances sont très importantes, il est donc préférable d’utiliser un algorithme modulaire pour réduire les calculs. C'est ici le rôle du pow(a,k,n-1). Il permet de remplacer $a^{k}mod(n-1)$ et donc de gagner beaucoup de temps lors de l’exécution. En effet, la fonction modulaire pow permet de calculer le résultat modulaire rapidement. Le programme ne calculera pas la valeur exacte de la puissance (parfois très importante) pour ensuite calculer son modulo N. Cela permet de gagner beaucoup de temps lors de l’exécution.

randrange(2,n-1) permet de tirer au hasard un nombre a compris entre 2 et n-1. C'est cette partie qui fait du test de Fermat un test probabiliste.

Le Test de Miller-Rabin

Son fonctionnement

Ce test fonctionne de la même façon que le test de Fermat mais effectue plus de tests sur les résultats des puissances modulo N. Il s'agit donc d'un test probabiliste. Si ce test se trompe, c'est généralement pour des nombres petits. Pour éviter cela, il est nécessaire d'ajouter un petit test pour les multiples de 2 et de 3 dès le début du programme. Grâce à des fonctions modulaires, il est très fiable en ce qui concerne les grands entiers.

Programmation en python

def miller_rabin(n, k):

   """ en entree : n l'entier a tester
                           k le compteur
       en sortie: un booleen (True si premier)"""
   if n == 2 or n ==3 :
       return True
   if n % 2 == 0:
       return False
   r, s = 0, n - 1
   while s % 2 == 0:
       r += 1
       s //= 2                     # la partie non paire de n-1 / permet la factorisation en nombre premier
   for _ in range(k):
       a = randrange(2, n - 1)     
       x = pow(a, s, n)            
       if x == 1 or x == n - 1:
           continue                
       for _ in range(r - 1):      
           x = pow(x, 2, n)        
           if x == n - 1:
               break               
       else:
           return False            
   return True  

N-1 est forcément paire car dès le début du test on vérifie la condition N impair sinon res = false Dans ce code, on utilise plusieurs boucles spécifiques dans le but de simplifier le code et de permettre au programme de s'effectuer plus rapidement.

Continue

Cette partie de code permet de relancer le for qui la précède. Ainsi, continue permet de ne pas passer à la suite, tant que le condition est vérifiée.

La boucle For / Else

C'est une boucle spécifique à python: On effectue la boucle for; si on ne rencontre pas de break , alors on passe dans le break ; sinon, lorsque l'on rencontre le break, on passe directement au return. Le break a pour but de sortir de la boucle.

L'objectif de cette boucle est de ne pas définir une nouvelle variable True/False et donc de supprimer un test.

Xrange

Une partie Xrange pourrait être ajoutée dans la seconde boucle for. Celle ci permettrait de ne pas avoir à créer une liste comme peut le faire range. Cela permettrait au programme d'être encore plus rapide mais cette fonction ne fonctionne pas avec toutes les versions de python, il était donc ici plus judicieux de ne pas la mettre.

Comparaison des programmes

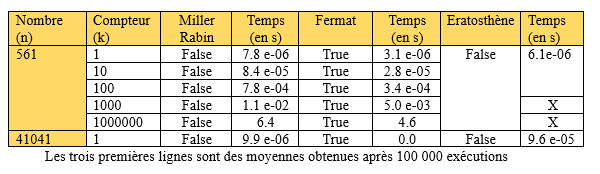
En fonction du temps

Le Crible d’Ératosthène étant un test déterministe, il sera forcément plus long à l'exécution que les tests probabilistes. Le test de Fermat sera en réalité le test le plus rapide. En effet il effectue moins de tests que Miller Rabin. Mais, le test de Miller Rabin a l'avantage d'être le compromis entre le Crible d’Ératosthène et le test de Fermat. En effet, celui ci s'effectue assez rapidement et se trompe très rarement.

Fonction python pour calculer le temps d'exécution

def temps_de_...(n,k,t):

         tps = time.time()
         sol = 0
         for i in range(t):
         res = #mettre la fonction voulue faisant le test de primalité
             if res == True:
                sol +=1
         theta = time.time() -tps
         print(theta/t)
         print('Pourcentage de True:')
         print(sol/t*100)

Il est important de regarder Un pourcentage de True obtenu. Sinon la fonction risque de renvoyer simplement le résultat du dernier test effectué.

Test de sûreté

Le calcule du pourcentage de True dans le code précédent permet déjà d'obtenir des données sur la fiabilité. Il est possible d'utiliser une fonction telle que isprime() de la bibliothèque sympy chez python pour vérifier la sûreté de nos tests. En effet, cette fonction est très fiable.

Exemple de code pour nos trois tests

def surete(t,k=10):

   cp_mr = 0
   cp_f = 0
   cp_e = 0
   for i in range(t):
       r= randint(2,1000000000000)
       n=2*r+1
       rep = isprime(n)
       era = eratosthene(n)
       fer = fermat(n,k)
       mr = miller_rabin(n,k)
       if rep == mr:
           cp_mr +=1
       if rep == era:
           cp_e +=1
       if rep == fer:
           cp_f +=1
   print('Fiabilité miller_rabin :')
   print(cp_mr/t*100)
   print('Fiabilité ératosthène :')
   print(cp_e/t*100)
   print('Fiabilité fermat :')
   print(cp_f/t*100)

Cette fonction va tirer des entiers N impairs au hasard. Isprime() permettra de vérifier les réponses données pour chaque N par chaque fonction. Ainsi il est possible d'obtenir un pourcentage de fiabilité de chaque test. A noter que plus t (l’échantillonnage) sera grand, plus la fiabilité sera précise.

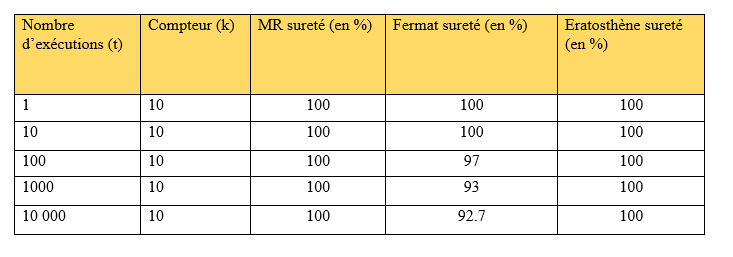
Résultats obtenus :

Des erreurs possibles

On observe que les programmes ne sont pas tous sûrs à 100%. C'est d'ailleurs le principal risque des programmes probabilistes.

Miller Rabin

Si on trouve a et N tel que a^{2}^{N-1}^{s} mod(N) = +/- 1 Alors le programme va forcément se tromper.

Fermat

Si on trouve a et N tel que $a^{N-1}mod(N)=+/-1$ Alors le programme va forcément se tromper.

Ce programme va par ailleurs toujours se tromper pour les Nombres de Carmichael.

Les nombres pseudos premiers

Les nombres pseudos premiers sont des nombres premier probable, ils partagent une propriété commune à tous les nombres premiers. Mais malgré ces propriétés, ils ne sont pas premiers.

Pseudos premiers absolus

On peut dire que des nombres sont pseudos premiers absolus si pour toute valeur de a, la version dite faible de Fermat est vérifiée.

Nombres de Carmichael

On a un nombre de Carmichael si la version forte de Fermat est vérifiée pour toute valeur de a. Ainsi, ce sont les nombres pour lesquels le théorème de Fermat se plante à chaque fois.

D’après la preuve faite par Alfort, Grandville et Pomerance en 1994, il existe une infinité de nombres de Carmicahel. De plus, ils ont toujours au moins 3 facteurs, tous impairs et aucun de ces facteurs n’est carré.

Tests :