Automates cellulaires

Ce projet avait pour but d'étudier le fonctionnement des automates cellulaires et les caractéristiques particulières que l'on peut retrouver chez certains.

Définitions

Définition simple

Un automate cellulaire est une grille régulière dont les cases sont appelées « cellules ». Chacune a un « état » parmi un ensemble fini. L'état d'une cellule au « tour » t+1 est définit en fonction de cet état et celui de l'ensemble fini de cellules « voisinage » au tour t, par la « règle » de l'automate cellulaire. Lorsque toutes les cellules ont été mises à jour, on parle de « génération ».

Pour un automate de 2 dimensions les voisinages les plus courants sont celui de von Neumann et celui de Moore. (en vert et rouge les cellules appartenant au voisinage de la cellule rouge.)

Définition formelle

Un automate cellulaire $A$ est définit par le 4-uplet $(d,Q,V,\delta )$ tel que :

• $d$ est un entier positif, la dimension de $A$. Son réseau est donc $\mathbb {Z} ^{d}$
• $Q$ est l'ensemble fini des états des cellules de $A$
• $V\subseteq \mathbb {Z} ^{d}$, un sous-ensemble fini du réseau, le voisinage. $V=\{v_{1},\ldots ,v_{a}\}$
• $\delta :Q^{a}\rightarrow Q$ est la règle locale avec $a=|V|$

On peut donc définir la fonction globale d'évolution de l'automate $F_{\delta }:Q^{\mathbb {Z} ^{d}}\rightarrow Q^{\mathbb {Z} ^{d}}$ définit par $F_{\delta }(c)=z\mapsto \delta {\bigl (}c(z+v_{1}),\ldots ,c(z+v_{a}){\bigr )}$ pour tout $c\in Q^{\mathbb {Z} ^{d}}$

Classifications

Bien que les deux classifications qui sont décrites ci-dessous peuvent être retrouvées dans les travaux de certains chercheurs, il est commun de décrire un automate en fonction de leurs caractéristiques particulières sans pour autant les séparer en classes.

Classification de Wolfram

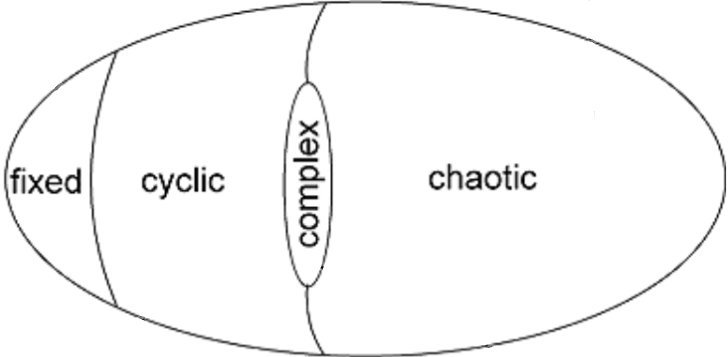
Stephen Wolfram classe les automates cellulaires en 4 classes selon leur comportement avec des configurations initiales aléatoires :

1. Stable : Après un certain nombre de générations, une configuration se répète à l'infini.
2. Cyclique : Après un certain nombre de générations, une série de configurations se répètent périodiquement.
3. Chaotique : Comportement chaotique et génération de motifs apériodiques.
4. Complexe : Apparition de structures complexes possédants divers propriétés comme la capacité de se mouvoir ou de se préserver malgré des perturbations.

L'une des principales critiques de cette classification réside dans son incapacité à déterminer si un automate cellulaire est Turin-universel, venant du fait que Wolfram ne définit la classe qu'à partir de configurations initiales aléatoires, mais pas de structure particulière créée spécifiquement. Malgré cela, cette classification reste la plus étudiée.

Christopher Langton propose d'envisager ces classes dans un continuum.

Classification d'Eppstein

Il existe une deuxième classification, proposée par David Eppstein. Les automates sont séparés en 4 classes :

1. Expansion obligatoire : N'importe quel motif initial s'étend indéfiniment dans toutes les directions.
2. Expansion impossible : Aucun motif ne peut s'étendre au-delà de ses limites initiales.
3. Contraction impossible : Les motifs ne s'étendent pas forcément indéfiniment, mais ne peuvent jamais se réduire en-deçà de leur limites initiales.
4. Expansion et contraction possibles : Seuls ces cas peuvent contenir des vaisseaux.

À l'heure actuelle, les automates qui ont été prouvés Turing-universels appartiennent tous à la 4ème classe. Cependant il n'a pas été démontré que les autres classes ne peuvent pas contenir d'automate Turing-universel puisqu'il existe d'autres façons de transmettre des informations que les vaisseaux.

Les familles d'automates cellulaires célèbres

Il existe de nombreuses familles d'automates cellulaires, mais nous n'en verrons que deux ici.

Les automates cellulaires élémentaires

Cette famille est la plus simple des automates cellulaires. Ses membres n'ont qu'une dimension et deux états. Le voisinage d'une cellule est composé de celles directement à sa droite et sa gauche et d'elle-même.

Puisque le voisinage prend 3 cellules et que chacune d'elles a un état parmi 2, on a $2^{3}=8$ motifs possibles. Pour chaque motif il y a 2 résultats possibles, donc $2^{8}=256$ règles possibles pour un automate cellulaire de cette famille. Depuis les travaux de S. Wolfram sur cette famille, chacune de ces règles est nommée par le résultat de ses motifs convertit en décimal. Ainsi, la règle suivante est la 103 : Car

111   110   101   100   011   010   001   000
 0     1     1     0     0     1     1     1

Soit $01100111_{(2)}=103_{(10)}$

Règles intéressantes

Certaines de ces 256 règles ont des propriétés particulières. Voici 3 d'entre elles :

Règle 22

Lorsque la configuration initiale est composée d'une seule cellule vivante on obtient une approximation du triangle de Sierpiński.

Règle 30

Selon Wolfram Research, en raison de son comportement local imprévisible et son comportement global chaotique, cet automate cellulaire peut être utilisé comme générateur de nombres pseudo-aléatoires.

Règle 110

Cette règle a été prouvée Turing-universelle.

Automates cellulaires type "Vie"

Ces automates sont bidimensionnels et utilisent le voisinage de Moore. Leurs règles peuvent toutes s'écrire sous la forme $Bx_{1},...,x_{n}/Sy_{1},...,y_{m}$ avec $x$ le nombre de cellules voisines vivantes nécessaires pour qu'une cellule puisse naître et $y$ le nombre de cellules voisines vivantes nécessaires pour qu'une cellule puisse survivre.

Le jeu de la vie de John H. Conway

Le jeu de la vie est certainement l'automate cellulaire le plus connu du grand publique. Il a été imaginé par John H. Conway en 1970.

Sa règle est la suivante :

• Une cellule morte nait si elle a exactement 3 cellules voisines vivantes
• Une cellule vivante survie si elle a 2 ou 3 cellules voisines vivantes.
• Dans les autres cas elle sera morte.

Cette règle peut donc s'écrire $B3/S23$.

Malgré cette règle simple, le jeu de la vie permet d'obtenir une grande variété de type de structures :

• Des structures stables, comme le bloc
• Des structures périodiques, comme le clignotant
• Des vaisseaux, structures mouvantes, comme le planeur
• Des mathusalems, structures qui vont mettre du temps avant de se stabiliser, comme le pentomino R
• Des cannons, structures créant des vaisseaux à un rythme parfois imprévisible, comme le Gosper Glider Gun
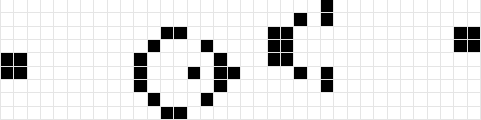
• Des puffeurs, vaisseaux laissant une trainée de débris, comme le Switch Engine
  • Il existe des puffeurs particuliers, les rakes qui agissent à la fois comme des puffeurs et comme des canons, leur débris étant composés de vaisseaux, comme le backrake 1
  • Il existe également des puffeurs dits spacefillers, dont les débris remplissent tout l'espace d'un motif régulier, comme le Max

Cet automate est Turing-universel et intrinsèquement universel.

Universalité

On distingue 2 types d'universalité pour les automates cellulaires.

Universalité Turing

Un automate cellulaire dit Turing-universel a la capacité de simuler une machine de Turing. Il donc capable de réaliser n'importe quel calcul. Plus généralement on accepte comme Turing-universel les automates cellulaires capables de simuler un système Turing-complet.

Universalité intrinsèque

Un automate cellulaire dit intrinsèquement universel est capable de simuler pas à pas n'importe quel automate de même dimension. L'automate simulateur utilise des groupes de cellules identiques et réguliers, chaque groupe représentant une seule cellule de l'automate simulé. L'automate simulateur peut utiliser plusieurs tours pour simuler une étape de l'automate simulé. Chaque état de l'automate simulé a au moins une configuration correspondante dans l'automate simulateur.

Remarque sur l'écriture des règles automates cellulaires

Il existe de nombreux formats pour donner la règle d'un automate. Pour un automate élémentaire, on utilisera la concaténation de ses résultats pour chaque motif en binaire ou décimal. Pour un type "Vie" on utilisera le format B/S. Pourtant nous avons vu au début que l'écriture formelle de la règle d'un automate cellulaire était celle d'une fonction^[1]. La raison est plutôt simple : Pour l'instant, il n'existe pas d'algorithme capable de générer n'importe quel automate cellulaire de manière optimisée, donc la plupart des logiciels de visualisation d'automates cellulaires préfèrent se concentrer sur certains types d'automates. Il n'est pas ardu pour autant de faire un générateur universel, il sera seulement très lent. C'est d'ailleurs ce que j'ai tenté de faire avec ce programme, écrit en python. [Voir le projet sur GitHub]