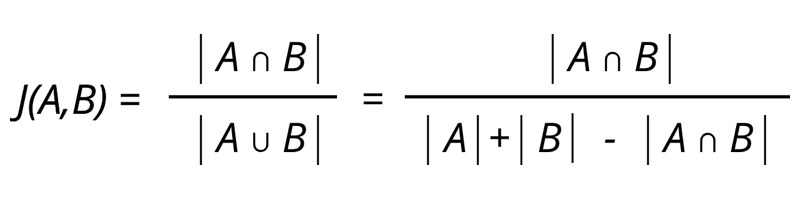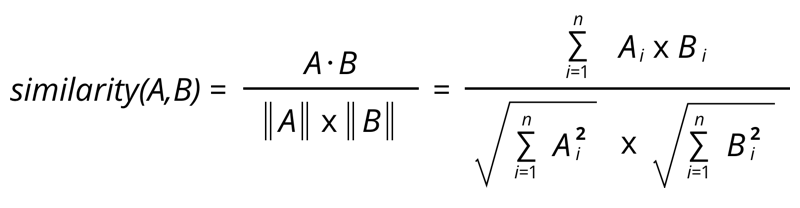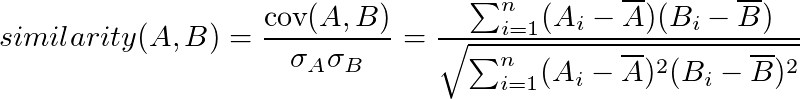Base de données orientées Graphe, similarité et recommandation
Aujourd'hui les bases de données sont partout. Avec la quantité d'information à stocker, il a fallu inventer des moyens de les stocker. Au début il y avait des bases de données relationnels qui pouvaient stocker de l'information en grande quantité mais ne permettaient pas de gérer les relations entre les éléments de la base. C'est pour cela que les bases de données orientées Graphes ont vu le jour.
Les bases de données orientées Graphes :
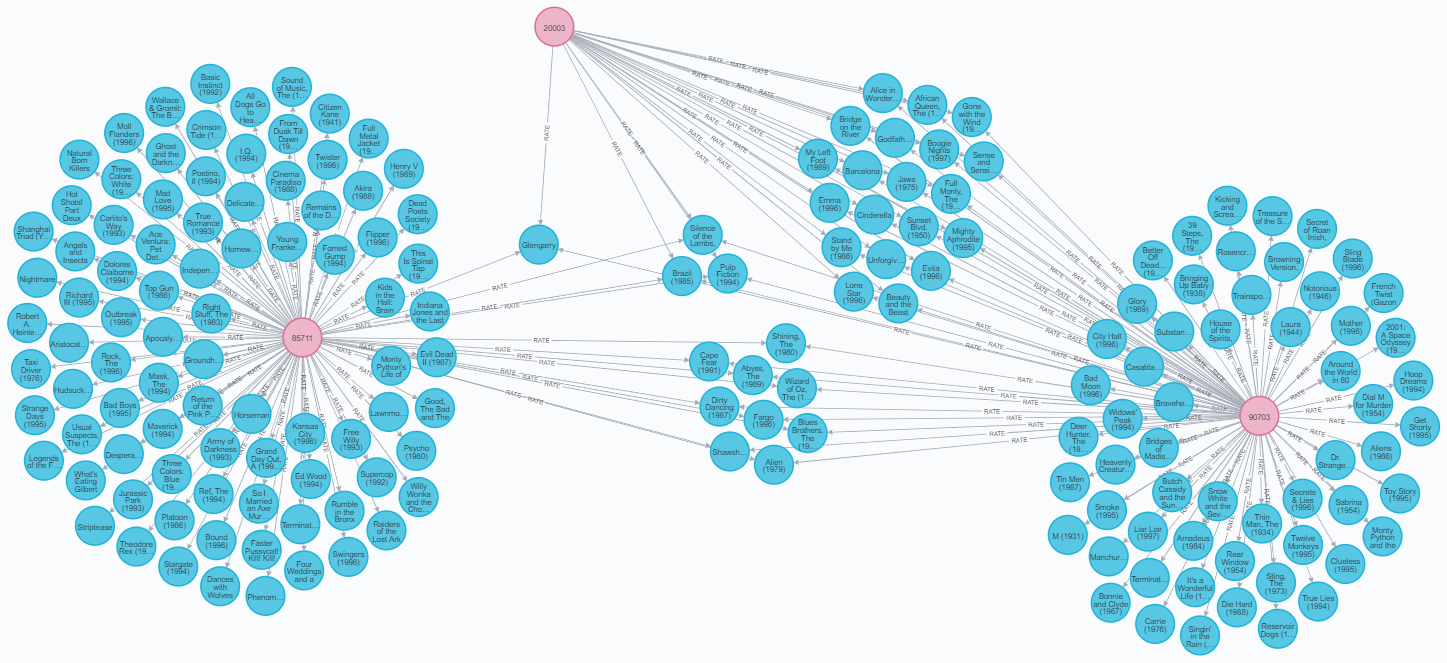
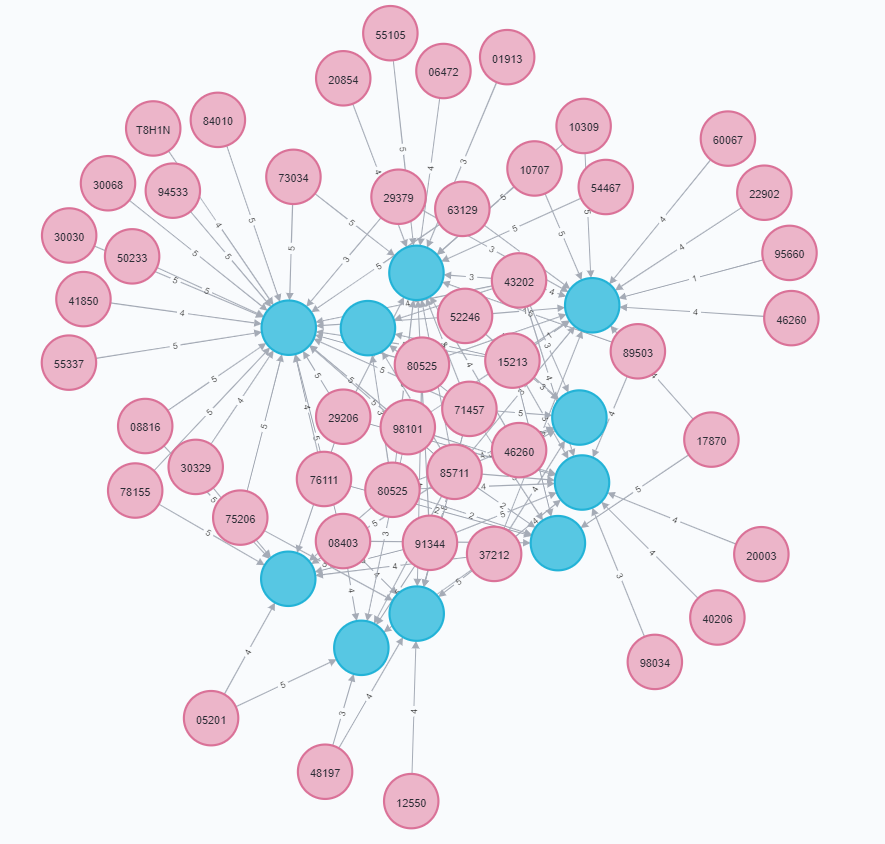
Les bases de données orientées Graphes peuvent stocker des éléments comme des individus ou des objets, mais également les relations entre les éléments. Les éléments sont ce qu'on appelle des nœuds, et les liens des arêtes. On les représente comme ceci :
On voit ici différents nœuds représentés par des cercles de couleur, et leurs liens par des flèches les reliant. Chaque nœud peut avoir des données personnelles, ici ce sont des individus en rose qui ont un nom, un métier, un genre etc... Idem pour les nœuds bleu qui représentent des films qui ont un titre, un genre, une date etc...
Cette représentation permet d'avoir un effet très visuel pour analyser les informations de ces bases. On va ainsi pouvoir rapprocher les liens en créant des chemins. En effet avec tous ces liens on peut facilement relier les éléments entre eux en parcourant une série de lien, ce qu'on va appeler un chemin. Par exemple sur l'image ci-dessus on voit que les individus de gauche et de droite sont reliés par des films qu'ils ont en commun, ainsi on peut les relier soit directement soit à l'aide d'un utilisateur intermédiaire.
Recherche de similarité :
Avec le grand nombre d'information et de choix qui nous sont offerts aujourd'hui, il est difficile de prendre une décision soit même, trop d'information nous empêche de faire un choix implicite car il nous est impossible de tout analyser. C'est pourquoi la recommandation est très présente de nos jours, elle compare un nombre énorme d'information pour sortir un choix qui n'est pas évident à voir au premier abord.
Pour cela on peut se servir des bases de données orientés graphes pour rapprocher les individus selon leur ressemblance et ainsi obtenir des éléments recommandables. Pour tester cette ressemblance nous allons utiliser des algorithmes de similarités. Trois algorithmes ont été vus lors de ce projet :
La similarité de Jaccard
Elle consiste en la comparaison des éléments partagés de 2 individus. L’indice de Jaccard va de 0 pour aucune similarité à 1 pour une similarité très grande. Cet indice s’obtient en faisant le quotient de l’intersection des éléments des 2 individus, ce qu’ils ont en commun, sur l’ensemble des éléments des 2 individus. Cet indice permet de voir la similarité entre 2 personnes mais ne prend pas en compte l’avis des individus. En effet les liens peuvent être pondérés, ce que Jaccard ne prend pas en compte.
Soit 2 ensembles de liens, la formule s'obtient donc par le quotient des éléments partagés par les deux ensembles sur tous les éléments des ensembles.
La similarité Cosinus
Elle consiste en la comparaison des avis des individus à l'aide des liens pondérés, cela permet de prendre en compte les avis des individus sur leur lien. L’indice peut donc aller de -1 à 1, -1 signifiant une similarité opposée, 0 pour aucune similarité, et 1 pour une similarité parfaite. Cette méthode possède quand même des inconvénients, en effet elle ne prend pas en compte l’échelle des avis. Pour un individu, une certaine note ne correspondra pas forcément à la même note pour un autre individu alors que le ressenti est le même.
La formule s'obtient en se basant sur les mathématiques en voyant les ensembles de liens pondérés comme des vecteurs. On a donc le quotient du produit scalaire des 2 vecteurs sur le produit des normes des deux vecteurs
La similarité de Pearson
La similarité de Pearson se base sur les statistiques. A l’aide de la covariance et de l’écart à la moyenne, on obtient une similarité qui prend en compte les valeurs des liens. Grace à cette notion de moyenne on enlève ce problème d'échelle de la similarité cosinus et on obtient ainsi une similarité qui se fie aux tendances des avis.
La formule s'obtient en faisant le quotient de la covariance entre 2 ensembles sur la somme de leur écart type.
Requêtes Cypher, Neo4j
Pour gérer ces bases de données orientés Graphes, j'ai utilisé le logiciel Neo4j qui permet de faire des requêtes simples pour interagir avec les différents éléments de la base. Pour gérer ces bases on utilise des requêtes cypher, ce sont des appels dans la base pour récupérer certains éléments avec une certaine syntaxe. On identifie un noeud entre parenthèse, et un lien entre crochet, avec des flèches pour les relier.
Dans le projet j'ai pu utiliser une base de données publique nommée MovieLens, qui regroupe des utilisateurs et des films en les reliant selon les notations qu'ils ont mis sur les films qu'ils ont pu voir. On peut ainsi la gérer et récupérer des éléments selon leurs liens.
Ici on voit un exemple d'une requête qui associe un individu 1, tous les films qu'il a pu noter, et tous les utilisateurs qui ont également noté ce film. Et on obtient le résultat ci-dessous.
MATCH(u1:User {id:'1'})-[:RATE]->(m:Movie)<-[:RATE]-(u2:User)
RETURN u1, u2, m LIMIT 100
On voit ainsi qu'à l'aide d'une simple commande assez visuelle on peut récupérer des liens tout de suite nombreux et complexes.
A l'aide de ces requêtes cypher, on peut ainsi récupérer un individu arbitraire et appliquer les différents algorithmes de similarité vu plus haut pour obtenir tous les individus qui lui sont similaire. Voici donc les requêtes cypher que j'ai obtenu pour chaque algorithme :
Similarité de Jaccard :
//RECUPERE LES UTILISATEURS POTENTIELS
MATCH (u:User {id:'1'})-[:RATE]->(m:Movie)<-[:RATE]-(all:User)
MATCH (u)-[:RATE]->(m1:Movie), (all)-[:RATE]->(m2:Movie) WITH u, collect(m1) AS seen_by_u, collect(m2) AS seen_by_all, all
//APPLIQUE LA FORMULE
MATCH (m3:Movie) WHERE m3 IN seen_by_all AND m3 IN seen_by_u
MATCH (m4:Movie) WHERE m4 IN seen_by_all OR m4 IN seen_by_u
WITH u, count(distinct m3) AS A, count (distinct m4) AS B, all
WITH u, toFloat (A) / toFloat(B) AS Jaccard, all
RETURN all.id as ID, Jaccard ORDER BY Jaccard DESC
Similarité Cosinus :
//RECUPERE LES UTILISATEURS POTENTIELS
MATCH (p1:User {id: '1'})-[x:RATE]->(m:Movie)<-[y:RATE]-(p2:User)
//APPLIQUE LA FORMULE
WITH COUNT(m) AS nbmovie, SUM(x.rating* y.rating) AS xyDotProduct,SQRT(REDUCE(xDot= 0.0, a IN COLLECT(x.rating) | xDot+ a^2)) AS xLength,SQRT(REDUCE(yDot= 0.0 , b IN COLLECT(y.rating) | yDot+ b^2)) AS yLength,p1, p2 WHERE nbmovie> 10
RETURN p2.id as ID, xyDotProduct/ (xLength* yLength) AS Cosinus order by Cosinus DESC
Similarité de Pearson :
//RECUPERE LES UTILISATEURS POTENTIELS
MATCH (u1:User {id:"1"})-[r:RATE]->(m:Movie)
WITH u1, avg(r.rating) AS u1_mean
MATCH (u1)-[r1:RATE]->(m:Movie)<-[r2:RATE]-(u2:User)
WITH u1, u1_mean, u2, COLLECT({r1: r1, r2: r2}) AS ratings
MATCH (u2)-[r:RATE]->(m:Movie)
//APPLIQUE LA FORMULE
WITH u1, u1_mean, u2, avg(r.rating) AS u2_mean, ratings
UNWIND ratings AS r
WITH sum( (r.r1.rating-u1_mean) * (r.r2.rating-u2_mean) ) AS nom,
sqrt( sum( (r.r1.rating - u1_mean)^2) * sum( (r.r2.rating - u2_mean) ^2)) AS denom,
u1, u2 WHERE denom <> 0
RETURN u1.id, u2.id, nom/denom AS pearson, nom, denom
ORDER BY pearson DESC LIMIT 100;
Résultats
Pour chaque requête on obtient ainsi une liste de personnes similaires à un individu arbitraire. Chaque liste est différente car les algorithmes de recherche n'ont pas les mêmes critères de similarité :
Similarité de Jaccard :
╒═══════╤════════════════════╕ │"ID" │"Jaccard" │ ╞═══════╪════════════════════╡ │"56" │0.15422885572139303 │ ├───────┼────────────────────┤ │"94" │0.14909090909090908 │ ├───────┼────────────────────┤ │"62" │0.1388888888888889 │ ├───────┼────────────────────┤ │"44" │0.13043478260869565 │ ├───────┼────────────────────┤ │"16" │0.11827956989247312 │ ├───────┼────────────────────┤ │"49" │0.1036036036036036 │ ├───────┼────────────────────┤ │"70" │0.09142857142857143 │ ├───────┼────────────────────┤ │"22" │0.08333333333333333 │ ├───────┼────────────────────┤ │"76" │0.07407407407407407 │ ├───────┼────────────────────┤ │"21" │0.07281553398058252 │ ├───────┼────────────────────┤
Similarité Cosinus :
╒════╤══════════════════╕ │"ID"│"Cosinus" │ ╞════╪══════════════════╡ │"22"│0.9852467896543129│ ├────┼──────────────────┤ │"70"│0.9837492333334621│ ├────┼──────────────────┤ │"60"│0.9793600224328365│ ├────┼──────────────────┤ │"16"│0.9779837447107504│ ├────┼──────────────────┤ │"99"│0.9776536312849162│ ├────┼──────────────────┤ │"18"│0.9774725191236509│ ├────┼──────────────────┤ │"28"│0.9734760839587974│ ├────┼──────────────────┤ │"64"│0.9718772305930494│ ├────┼──────────────────┤ │"13"│0.9672596423278736│ ├────┼──────────────────┤ │"72"│0.9672477415479701│ ├────┼──────────────────┤
Similarité de Pearson :
╒═════╤═════════════════════╕ │"ID" │"Pearson" │ ╞═════╪═════════════════════╡ │"61" │1.0 │ ├─────┼─────────────────────┤ │"33" │1.0 │ ├─────┼─────────────────────┤ │"100"│1.0 │ ├─────┼─────────────────────┤ │"17" │0.9947011416362146 │ ├─────┼─────────────────────┤ │"27" │0.993615127946772 │ ├─────┼─────────────────────┤ │"34" │0.9745307325900329 │ ├─────┼─────────────────────┤ │"66" │0.9673228854286368 │ ├─────┼─────────────────────┤ │"67" │0.9134610634044803 │ ├─────┼─────────────────────┤ │"19" │0.9085408022231299 │ ├─────┼─────────────────────┤ │"3" │0.9012761718387297 │ ├─────┼─────────────────────┤
Les résultats de Jaccard ne sont pas très élevés car je n'ai pu importer qu'une petite partie de la base MovieLens par soucis de place, ainsi le manque d'information fausse les résultats globaux d'où les indices peu élevés.
Recommandation
Avec tous ces résultats, on peut alors récupérer les individus les plus similaires, puis les films qu'ils ont vus, filtrer ces films pour n'avoir que les films que l'individu arbitraire n'a pas vu, et ainsi obtenir un algorithme de recommandation. Les films les plus recommandables sont les films qui ont été vu par beaucoup de monde similaire, la récupération de ces films s'appelle le filtrages collaboratifs.
On obtient alors, ici avec la similarité de Cosinus, un tableau de films trié par ordre décroissant de pertinence, qui seraient aptes à plaire à l'individu sélectionné :
//RECUPERE LES UTILISATEURS LES PLUS SIMILAIRES AVEC COSINUS
MATCH (u:User {id: '1'})-[x:RATE]->(f:Movie)<-[y:RATE]-(all:User)
WITH
COUNT(f) AS nbmovie, SUM(x.rating* y.rating) AS xyDotProduct,SQRT(REDUCE(xDot= 0.0, a IN COLLECT(x.rating) | xDot+ a^2)) AS xLength,SQRT(REDUCE(yDot= 0.0 , b IN COLLECT(y.rating) | yDot+ b^2)) AS yLength, u, all
WITH nbmovie, u, all, xyDotProduct/ (xLength* yLength) AS csim order by csim DESC
//RECUPERE LES FILMS VUS PAR LES USERS LES PLUS SIMILAIRES (NON VU PAR USER 1)
MATCH (u)-[:RATE]->(m1:Movie), (all)-[:RATE]->(m2:Movie) WITH u, collect(m1) AS seen_by_u, collect(m2) AS seen_by_all, all
MATCH (m3:Movie) WHERE m3 IN seen_by_all AND NOT m3 IN seen_by_u
//TRI LES FILMS PAR NOTE & LES PLUS VUS
WITH DISTINCT(m3) AS m, count(m3) AS Liens
WHERE count(m3) > 5
MATCH (o:User)-[r:RATE]->(m)
RETURN m.title as Titre, avg(r.rating) AS Moyenne, Liens order by Liens desc, Moyenne desc
╒══════════════════════════════════════════════════════════════════════╤══════════════════╤═══════╕ │"Titre" │"Moyenne" │"Liens"│ ╞══════════════════════════════════════════════════════════════════════╪══════════════════╪═══════╡ │"Twelve Monkeys (1995)" │3.964285714285714 │28 │ ├──────────────────────────────────────────────────────────────────────┼──────────────────┼───────┤ │"Liar Liar (1997)" │3.0 │24 │ ├──────────────────────────────────────────────────────────────────────┼──────────────────┼───────┤ │"Star Wars (1977)" │4.416666666666666 │23 │ ├──────────────────────────────────────────────────────────────────────┼──────────────────┼───────┤ │"Return of the Jedi (1983)" │4.090909090909091 │22 │ ├──────────────────────────────────────────────────────────────────────┼──────────────────┼───────┤ │"Schindler's List (1993)" │4.285714285714285 │21 │ ├──────────────────────────────────────────────────────────────────────┼──────────────────┼───────┤ │"Fugitive, The (1993)" │4.0 │20 │ ├──────────────────────────────────────────────────────────────────────┼──────────────────┼───────┤ │"E.T. the Extra-Terrestrial (1982)" │3.9500000000000006│20 │ ├──────────────────────────────────────────────────────────────────────┼──────────────────┼───────┤ │"Toy Story (1995)" │3.9499999999999997│20 │ ├──────────────────────────────────────────────────────────────────────┼──────────────────┼───────┤ │"Apollo 13 (1995)" │3.9000000000000004│20 │ ├──────────────────────────────────────────────────────────────────────┼──────────────────┼───────┤ │"English Patient, The (1996)" │3.8500000000000005│20 │ ├──────────────────────────────────────────────────────────────────────┼──────────────────┼───────┤
Conclusion
Avec les bases de données orientées Graphes, on peut donc facilement récupérer des individus, leur appliquer des algorithmes de similarité pour trouver les personnes proches, pour ensuite leur appliquer des filtrages collaboratifs pour finalement obtenir des algorithmes de recommandation. Notre exemple est un algorithme plutôt simple, mais aujourd'hui sur internet principalement les algorithmes prennent en compte un nombre d'information énorme pour une plus grande précision.