Calcul approché de l'élément majoritaire, et autres algorithmes approchés
Introduction au problème
Lorsque nous avons besoin de traiter de grandes quantités de données en temps réel, nous avons souvent besoin de déterminer les éléments qui sont les plus fréquents, les plus significatifs. L'exemple le plus clair est celui des réseaux sociaux. Il faut déterminer parmi un flot de publications, lesquelles sont les plus adaptées pour l'utilisateur. Nous nous sommes donc intéressés aux algorithmes qui permettent de déterminer les éléments majoritaires.
Solution commune : un problème
La solution intuitive et parfaitement correcte est l'algorithme de majorité exacte qui compte précisément le nombre d’occurrences de chaque élément puis compare pour déterminer l'élément majoritaire. Nous pouvons l'écrire de différentes manières et l'algorithme sera plus ou moins rapide en fonction de la structure de donnée que nous utilisons. Nous avons choisit ici d'utiliser les dictionnaires, plus rapide que les listes.
Voici un algorithme python rapide qui réalise satisfait notre demande :
def elem_maj_dict(lst:iter):
"""Algorithme qui renvoi l'élément majoritaire avec 100% de réussite. On utilise ici les dictionnaires pour le rendre plus efficace."""
D = {}
for k in lst:
D[k] = D.get(k,0) + 1
maxi = 0
indice = 0
for el in D:
if D[el] > maxi:
maxi = D[el]
indice = el
return indice
Nous avons la complexité suivante :
Pour n éléments, il s'exécutera en temps n. À ce jour, il n'existe pas d'algorithme plus rapide en termes de complexité de vitesse pour cette tâche. On peut améliorer les performances, mais la complexité restera au moins O(n).
Le problème est que même le plus efficace de ces algorithmes à un inconvénient : l'occupation de la mémoire. Plus le nombre d’éléments est élevé, plus la mémoire requise est conséquente. Nous nous sommes donc demandé comment résoudre ce problème. Cet algorithme n'est donc pas adapté face à de grands volumes de données.
L'algorithme Space Saving, une solution
L'algorithme, introduction
L'algorithme Space Saving s'incarne en une alternative à peu près aussi rapide mais qui ne stocke pas les éléments. La mémoire dont il a besoin est considérablement plus faible que celle de l'algorithme classique.
Cependant, le résultat n'est pas toujours exact ! Pour certain cas d'utilisation, cela n'est pas un problème. L'algorithme a des propriétés (qui seront détaillées ci-bas) qui garantisse un résultat correct ou proche de l'optimum.
Ainsi, dans le cas notamment des réseaux sociaux, si une publication sur 30 parmi celles suggérées à l'utilisateur est fausse, cela n'est pas un problème au vu du gain de mémoire gagné.
Nous avons implémenté un algorithme Space Saving sur le langage python à l'aide des dictionnaires, qui rendent les opérations plus rapides qu'en utilisant les listes.
def ss_dict(lst:iter, n):
"""Algorithme space_saving qui renvoie les n éléments les plus fréquents
Algorithme réalisé avec des dictionnaires. Adapté aux itérateurs"""
lst = iter(lst)
compt = {} # Dictionnaires qui accueillera les éléments majoritaires
compteur = 0
while len(compt) < n: # Initialisation des compteurs
lm = next(lst) ; compteur += 1
compt[lm] = compt.get(lm, 0) + 1
for lm in lst:
compteur += 1
if lm in compt:
compt[lm] += 1
else:
for elem in compt:
if compt[elem] < compteur:
compteur = compt[elem] + 1
minim = elem
del compt[minim]
compt[lm] = compteur
return compt, n
L'algorithme, principe et propriétés
On initialise n compteurs si l'on souhaite n éléments, chacun d'entre eux a une valeur associée à un élément. Lorsque l'on a un nouvel élément, on a besoin de savoir quel élément a la plus petite valeur. On la remplace et on incrémente le compteur correspondant. Cela semble absurde à première vue mais cela devient logique lorsque l'on comprend son fonctionnement. Nous avons la propriété suivante :
Pour k compteurs, si un élément est présent plus que 1/k % des cas, alors l'élément sera à coup sûr renvoyé dans la liste des éléments majoritaires.
Par exemple, si on a deux compteurs, 5 éléments et que l'un d'entre eux est présent 3 fois, il sera forcément renvoyé dans la liste des deux éléments majoritaires.
Voici un exemple avec la distribution a, a, a, b, c et la distribution a, c, a, b, a
1 2
Avec l’algorithme sous cette forme, nous avons la complexité suivante :
Nous avons la complexité suivante :
On ne conserve pas tout les éléments. On à donc d'abord une complexité de mémoire de 0(k) avec k le nombre de compteurs. C'est un gain extrême en comparaison de notre premier algorithme. Là où pour 10 millions d'éléments le précédant prenait 10 millions d'emplacements, on à ici que l'on en à besoin que de 2.
En ce qui concerne la vitesse cependant, on à ici une complexité de 0(n*k). Cela s'explique. A chaque nouvel éléments on doit d'abord parcourir la liste de tout les compteurs avant de l'incrémenter ou d'effectuer une opération de remplacement.
La distribution Zipf
La distribution de Zipf est une loi de probabilité selon laquelle la fréquence d’un événement est inversement proportionnelle à son rang. En d'autres termes, dans une distribution de Zipf, le premier élément le plus fréquent apparaît environ deux fois plus souvent que le deuxième élément le plus fréquent, trois fois plus souvent que le troisième, et ainsi de suite. Cette distribution est fréquemment observée dans des phénomènes naturels et sociaux, comme la fréquence des mots dans une langue, la population des villes, et les requêtes sur les moteurs de recherche.
On dois au moins retenir de cette distribution que certains éléments apparaissent beaucoup plus que d'autres. Ainsi, lors des tests sur les résultats pour Zipf, l'algorithme était parfaitement adapté.
La structure de donnée Stream Summary
Les chercheurs ont développé une structure de données nommée Stream Summary qui s'implémente en programmation orientée objet. Elle possède la même complexité de mémoire que l'algorithme Space Saving classique mais réduit son temps d’exécution.
Ce code à été réalisé en POO (programmation orienté objet) qui utilise donc ce que l'on appelle des "classes" qui regroupe des fonctions qu'on appelle méthodes. Le code suivant à été simplifié et abrégé. Le réel code est disponible sur github (voir la section lien).
def space_saving(L, k):
S = StreamSummary(k) # On initialise un objet S de Stream Summary
for e in L: # Nous allons prendre un à un les éléments de L
S.update(e) # Et les ajouté avec une méthode de Stream Summary
return S.list() # On renvoie la listes des éléments majoritaires avec la méthode
class Cell:
add:
"""On ajoute l'élément dans une liste doublement chainée"""
...
pop:
"""On enlève l'élément d'une liste doublement chainée"""
...
class Counter(Cell):
init:
value = Valeur
E = Element
class Element(Cell):
init:
value = Valeur
C = Compteur
class StreamSummary:
"""C'est la classe principale qui est chargée d'appeler de gérer et de redéfinir les pointeurs à chaque itérations"""
init:
"""
On initialise la liste des compteurs, le dictionnaires d'éléments et une première liste E qui contient des elements inéxistants mais qui pointent vers le compteur 0
"""
...
update(k):
"""Ici, si l'élément k n'existe pas, on remplace un element de la liste par celui ci en conservant le compteur, conformément au code space saving. On incrément ensuie son compteur"""
Si l'élément est présent:
replace_min(k)
incr(k)
replace_min(k):
"""replace the first symbol with minimal counter by `k`"""
....
incr(k):
"""increase counter for symbol `k`"""
E = self.elements[k] # On prend l'élément k
C = E.C # On prend aussi le compteur de l'élément k
E.pop() # On supprime l'élément de sa liste
if C.E == E: # Dans le cas où le premier élément du compteur était l'élément supprimé
C.E = E.next # On définit la valeur suivante comme valeur du pointeur
if C.value + 1 == C.next.value: # On distingue deux cas. Dans le cas où le compteur suivant à la valeur du compteur actuel + 1
...
else: # Le deuxième cas : on doit crée ce compteur avec la valeur + 1
...
if C.E is None: # Si jamais, après avoir enlevé l'élément de sa liste initiale, celle ci est vide
C.pop() # On supprime le compteur de sa liste
if self.lst_compteurs == C: # Si le compteur était le premier de la listes des compteurs
self.lst_compteurs = C.next # On définit le premier élément de la liste des compteurs comme le compteur suivant
Grace à cette structure de données, nous parvenons à obtenir cette complexité :
On conserve la complexité de mémoire avantageuses de Stream Summary. En ce qui concerne la complexité de vitesse, on à de nouveau une complexité linéaire puisque le nombre d'opérations est borné.
Nous sommes donc parvenu à résoudre le problème de mémoire grâce à Stream Summary !
Comparatifs de temps d'exécutions
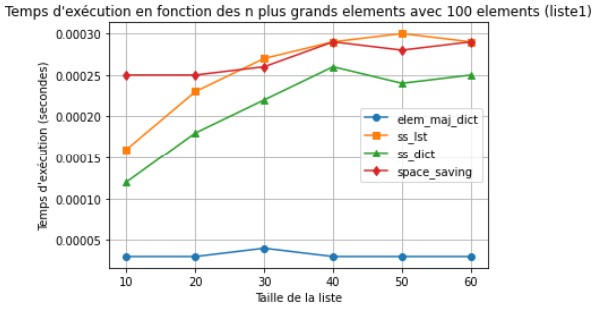
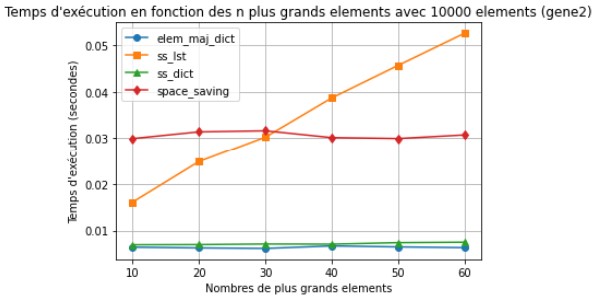
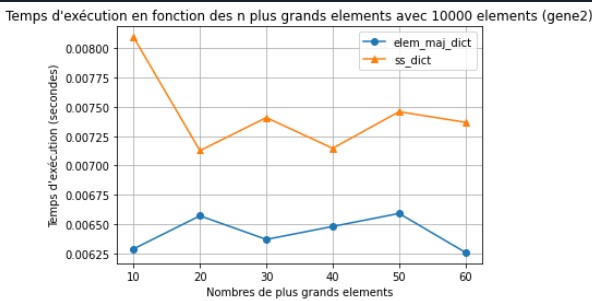
Nous connaissions la complexité du temps d’exécution de nos trois algorithmes mais nous avons cherché à la vérifier. Nous avons donc modélisé 5 graphes (attention, les résultats pour l'algorithme "élément majoritaire dictionnaire" ne sont pas significatif puisqu'il ne fonctionne qu'avec 2 compteurs, même lorsque l'on fait varier le nombre de compteurs) :
Ici nous voyons que le temps dépend uniquement pour l'algorithme Stream Summary du nombre d'éléments, de même que pour élément majoritaire dictionnaire.
Les résultat sont donc bien ceux qu'on attend.
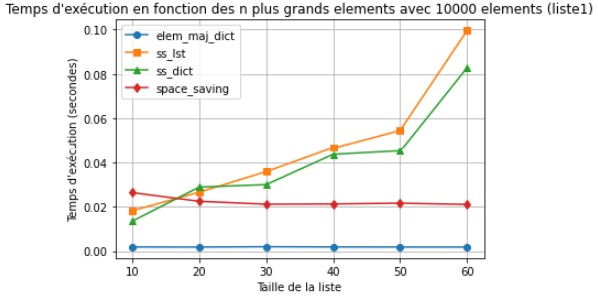
Lorsqu'on fait cette fois monter le nombre d'éléments, on observe bien que la complexité est linéaire, ou en tout cas qu'elle dépend bien de n.
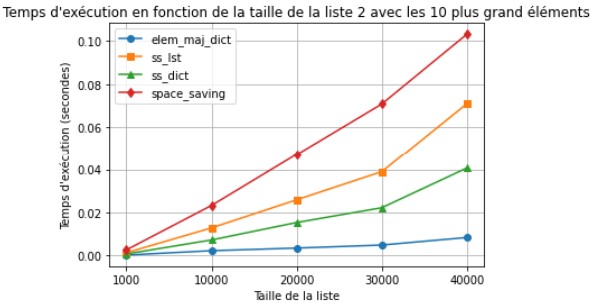
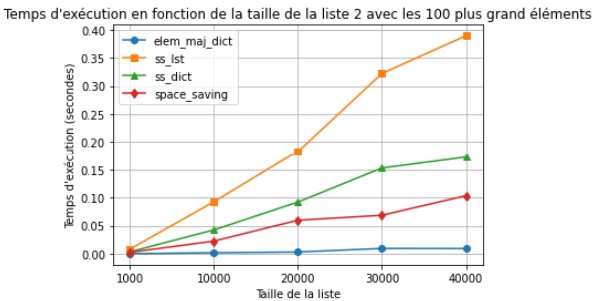
Ici nous faisons de nouveau varier le nombre de compteurs. Cependant, même avec beaucoup d'éléments, l'algorithme Space Saving avec les dictionnaire est plus rapide. Ici nous utilisons des générateurs, mon hypothèse est que le générateur est plus long pour envoyer des éléments, et que ceux-ci sont traités plus rapidement par Space Saving dictionnaire que par Stream Summary. Si tout les éléments étaient envoyés d'un coup, je pense que Stream Summary aurait été plus efficace.
Quelles applications, quels choix ?
On utilisera l'algorithme classique pour des ensembles de données de petite taille où la mémoire n'est pas un problème. Celui-ci nous fournira un résultat exact qui comptera toutes les occurrences de chaque élément. Cependant plus il y aura de données puis celui-ci deviendra incompatible et plus l'algorithme sera lent.
On utilisera la structure de données Stream Summary pour traiter de grands volumes de données ou pour travailler en temps réel. Cependant, selon la distribution de celle-ci, il y aura des imprécisions. Il n'est donc pas compatible avec toutes les situations.