Clustering par K-means, segmentation d'image
Etudiant : Paul AUBRY
Tuteur : Jacques-Olivier LACHAUD
Introduction : Clustering par k-means
Le clustering ou algorithme des k moyennes a pour but de regrouper des populations en communautés disposant de critères communs proches, jusqu'à avoir des communautés homogènes qu'on appellera cluster et qui ont pour représentant un centroïde.
Pour déterminer ces clusters, on regroupera les différents éléments en fonction d'une distance. Cette notion de distance est différente en fonction des domaines d'applications.
Le clustering par k-means peut être utilisé pour faire de la segmentation de clientèle, du clustering en Data Mining ou encore sur des images.
Algorithme pour l'image
|
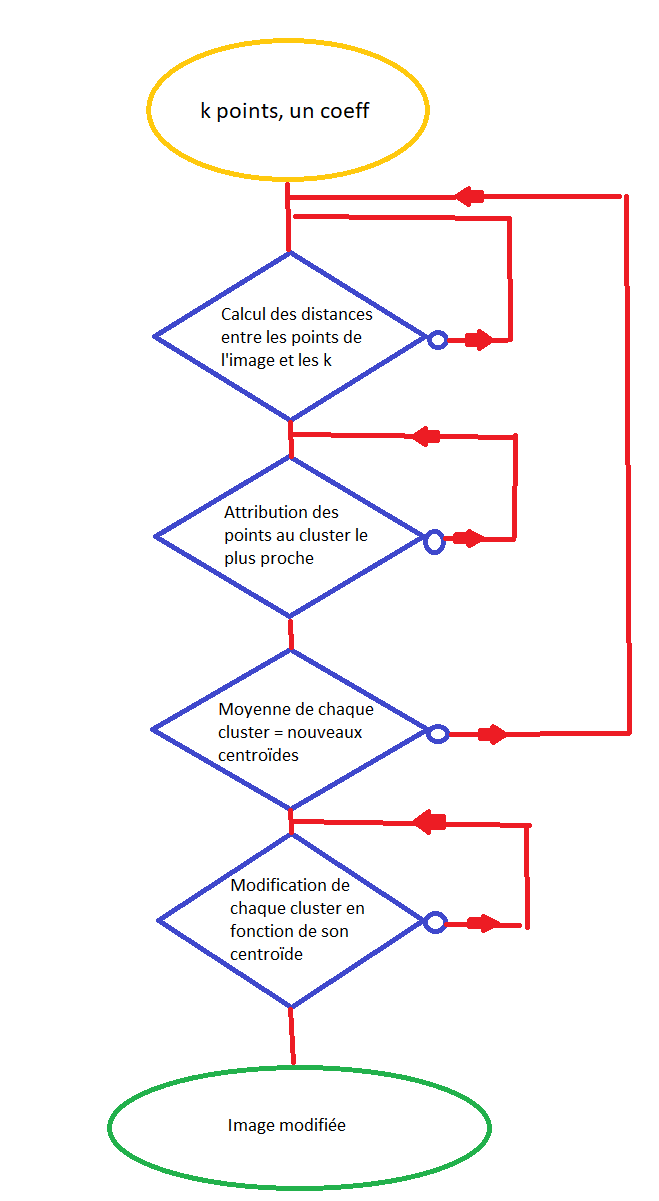
Nous allons voir ici, comment procéder de manière théorique, pour réaliser un clustering. Tout d'abord, nous devons choisir k points aléatoirement, qui seront les centroïdes, et un coefficient λ qui nous permettra de calculer les distances. Ensuite, nous allons affecter chaque point de l'image à un cluster. Pour cela, il faut calculer la distance entre le point, et chaque k. La distance la plus courte nous permettra de déterminer quel cluster choisir. Un point est représenté de la manière suivante : [ x , y , r , g , b ] . Avec x et y les coordonnées et r, g, b les composantes de couleurs. Pour calculer la distance on utilise la formule suivante :
Lorsque les clusters sont définis, on calcul la moyenne de chaque cluster, afin de récupérer de nouveaux centres. On réitère les actions vus précédemment mais cette fois-ci avec les nouveaux centres. Dès que l'on obtient des centres "stable", on peut modifier l'image. |
Réalisation grâce à Python
Pour ce faire, il faut installer plusieurs bibliothèques.
- "numpy", qui va nous servir à effectuer les calculs de manières bien plus rapide.
- "PIL" pour le traitement des images.
from random import * from PIL import Image import numpy as np
def clustering(k,coef):
"""Entrée :1 entier un flottant
Sortie : image modifiée"""
image0 = Image.open("Kowloon-small-329x216.png")
image = image0
l = image.width
h = image.height
tabImage = imageTab(image)
tabImageCoeff = coefficiente_valeur(tabImage, l, h)
centroides = meilleurs_centres(tabImage, tabImageCoeff, k, l ,h, coef, image)
coeffCentroides = coefficiente_valeur(centroides, l, h)
distance = distancePoints(tabImageCoeff, coeffCentroides,k,coef)
indice = distance_plus_courte(distance)
clusters = attribution_aux_clusters(tabImage,indice,k)
NumpyClusters = clustersEnNumpy(clusters,k)
print("En cours de finalisation...")
for i in range(0,k):
change_couleur_cluster( NumpyClusters[i] , centroides[i] , image )
image.save(str(k)+"-"+str(coef)+"Kowloon-small-329x216.png")
image.show()
image0.close()
image.close()
La variable tabImage contient le résultat de la fonction imageTab(), qui renvoit un tableau numpy, avec toutes les informations de chaque points de l'image, sous la forme [ x , y , r , g , b ].
Et la variable tabImageCoeff est égal à la fonction précédente mais avec chaque valeur du tableau entre 0 et 1.
La variable centroides calcul les meilleurs centroïdes sous la forme [ x , y , r , g , b ]. Et coeffCentroides et le même tableau mais avec les valeurs coefficentées.
Les variables qui suivent, permettent de calculer les distances entre les points et les centroïdes, pour ensuite créer les clusters dans la variable clusters.
Ensuite, la boucle for permet de changer la couleur des points de chaque clusters, avec les valeurs [r,g,b] du représentant du cluster.
Pour finir, l'image modifiée est enregistrée avec un nouveau nom.
Résultats
| J'ai pu obtenir ces résultats après deux minutes environ. On constate que les détails sont les mêmes, et on obtient des couleurs différentes. Plus le coefficient est petit, plus l'image est sombre. | |
| Quand le coefficient est égale à zéro, le traitement se fait juste sur les couleurs de l'image. Le programme fait une moyenne des couleurs. |
Pour une image de cette taille, une heure de traitement a été nécessaire. On remarque que les formes principales sont les mêmes, ainsi que les couleurs. Au niveau du ciel et du lac, on peut apercevoir que l'image a été traitée.