Cryptanalyse informatique de quelques systèmes de chiffrement "historiques"
Introduction
La cryptanalyse consiste à déduire un texte en clair d’un texte préalablement chiffré sans posséder la clé de chiffrement. Depuis des siècles, la cryptographie existe. La plus ancienne forme retrouvée date du XVIe siècle avant J.-C. Il s’agissait d’une tablette d’argile appartenant à un potier qui y avait gravé sa recette en supprimant des consonnes et en modifiant l’orthographe des mots.
Dans notre monde moderne, il existe de multiples façons de crypter un texte, toutes différentes les unes des autres et à complexités variables, certaines requérant l’usage de programmes informatiques afin de les décrypter dans des temps raisonnables. C’est pourquoi j’ai décidé d’étudier le chiffrement par substitution mono-alphabétique.
Substitution mono-alphabétique
La substitution mono-alphabétique est une dérivée améliorée du code de César. Elle consiste, comme son nom l’indique, à remplacer une lettre (ou autre) par une autre lettre (ou autre).
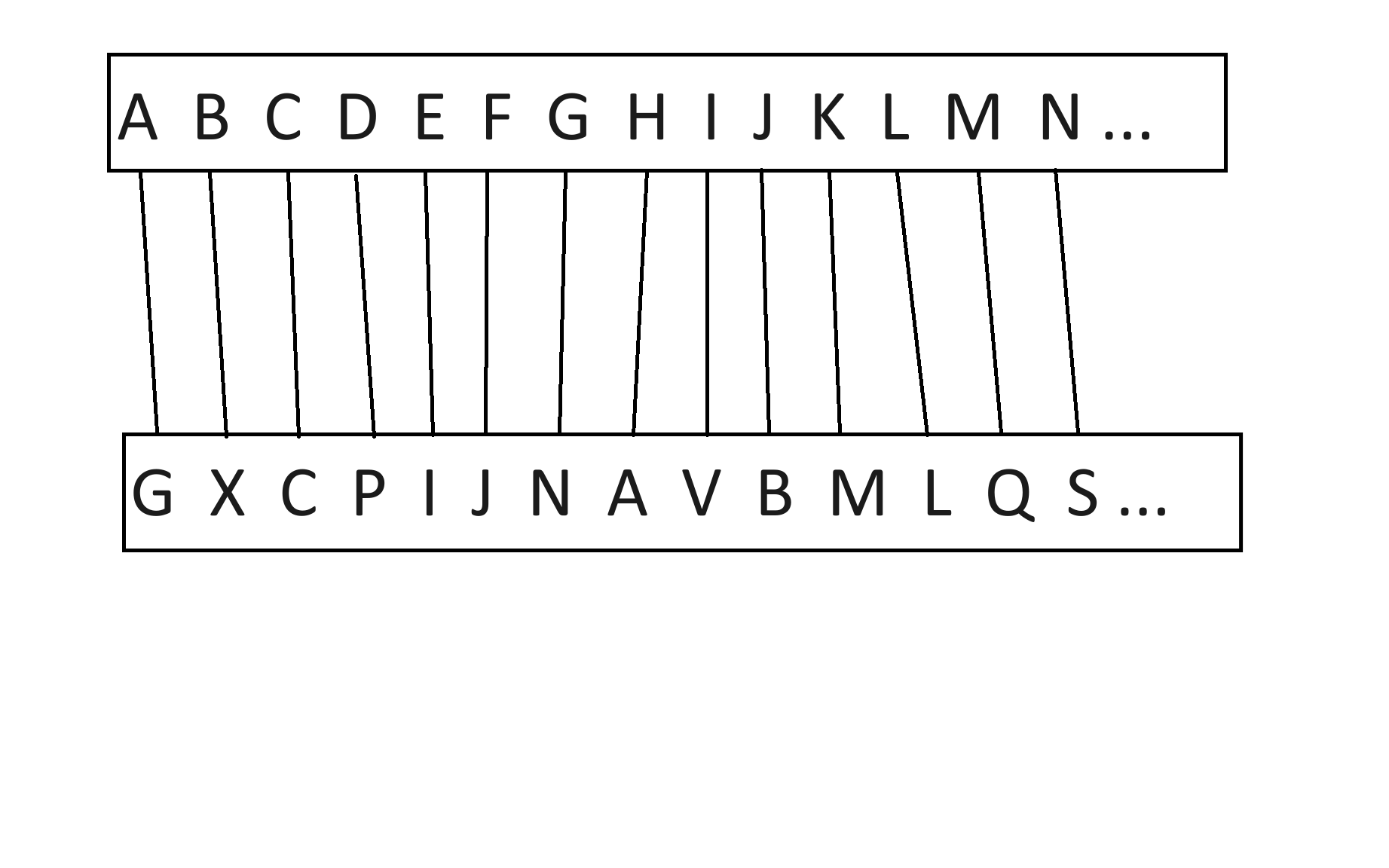
On se retrouve alors avec un texte clair (texte de base), un texte chiffré (texte après application du cryptage) et une clé de cryptage qui recense pour toutes les lettres par laquelle chacune est cryptée.
Exemple
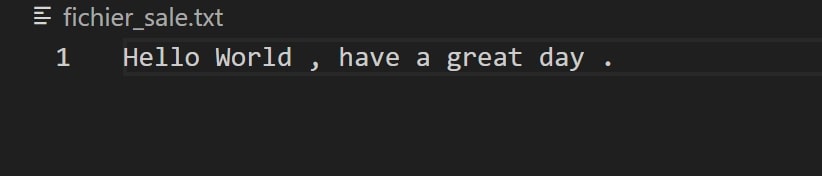
- Texte clair : Bonjour tout le monde
- Clé : A -> C, B -> F, C -> R, D -> K, E -> V, F -> T, G -> P, H -> M, I -> L, J -> Q, K -> W, L -> Z, M -> N, N -> S
- Texte chiffré : FKMWSCUCKFJCUNYUWIXCNY
Implémentation de la substitution mono-alphabétique
Pour cette étude, j’ai donc dû réaliser plusieurs fonctions de base et établir un dictionnaire de lettres que j’utiliserais pour mes tests.
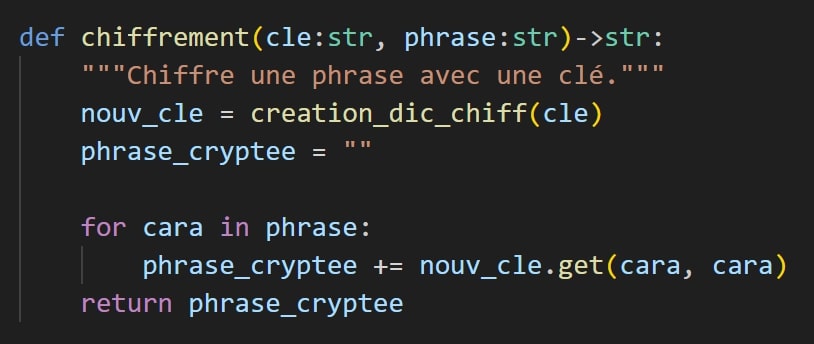
Chiffrement
On récupère la phrase et la clé de cryptage , avec cette clé on crée un dictionnaire du type {A:B,B:D,C:E;...} puis on change lettre par lettre la phrase.
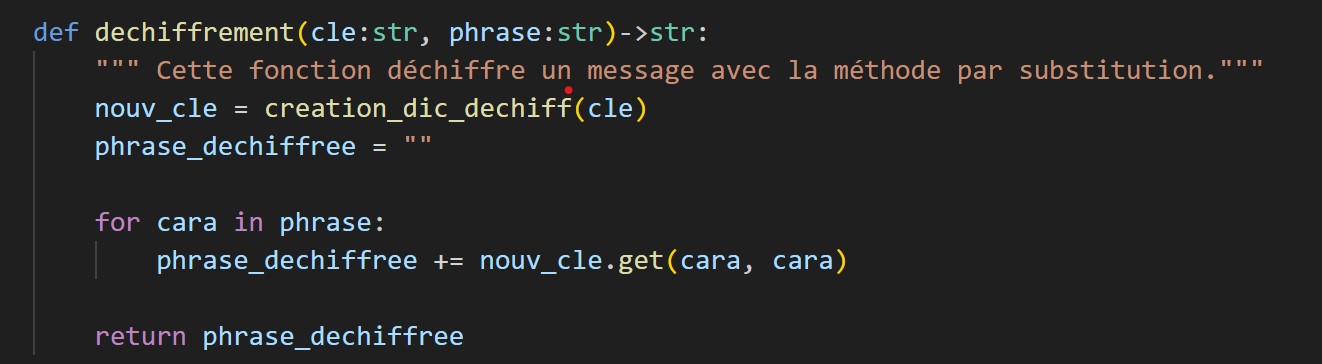
Déchiffrement
On récupère la phrase et la clé de cryptage , avec cette clé on crée un dictionnaire du type {B:A,D:B,E:C;...} puis on change lettre par lettre la phrase.
La différence est que le dictionnaire pour le chiffrement est du type {lettre: clé} et le déchiffrement du type {clé: lettre}.
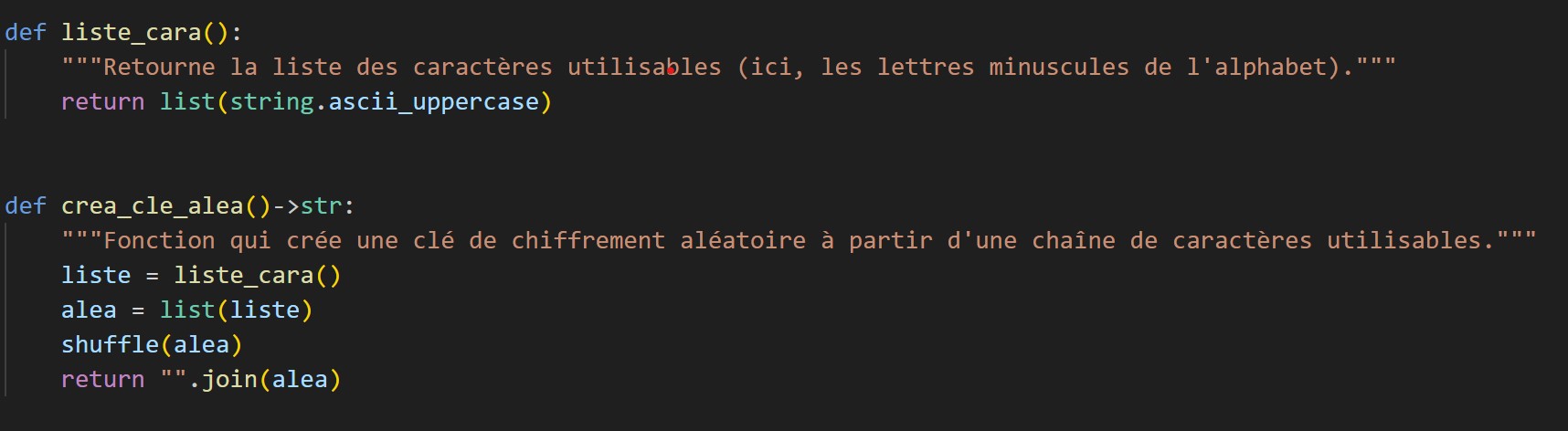
Création de clé (aléatoire)
Ici on récupère toutes les lettres de l'alphabets majuscules,( et on utilise la fonction shuffle pour avoir un ordre aléatoire. Celui-ci nous permet d'effectuer des tests plus arbitraires qu'avant).
Afin d’avoir un rendu propre, j’ai aussi créé une fonction permettant de « nettoyer le texte » me permettant de toujours travailler et faire des tests sur une même base de texte ( suppression de la ponctuation, espaces, retour chariot, …).
Nous avons donc une base, la possibilité de chiffré déchiffré un texte à l'aide d'une clé. A présent nous allons voir comment déchiffré un texte préalablement chiffré sans utilisé la clé.
Décryptage avec méthode de Hill-Climbing
Hill-Climbing définition
Le hill climbing est un algorithme itératif qui commence par une solution arbitraire et essaie d'améliorer cette solution de manière incrémentale. L'idée principale est de faire des modifications locales à la solution actuelle et de passer à une solution voisine si celle-ci présente une meilleure valeur de la fonction objectif (ou coût). Le processus se répète jusqu'à ce qu'aucune amélioration supplémentaire ne puisse être trouvée.
Caractéristiques
- Point de départ arbitraire : Dans notre cas, il s’agit de la clé aléatoire de base qu’on va utiliser pour décrypter le texte.
- Modifications locales : À chaque itération, l'algorithme examine les voisins de la solution courante pour trouver une solution améliorée.
- L’algorithme accepte toute solution améliorée sans garder en mémoire la précédente.
- Le processus ne fonctionne plus si on se trouve dans un minimum ou maximum local.
Calcul de score
Pour savoir si une solution est meilleure qu'une autre, nous allons nous baser sur un score calculé comme suit :
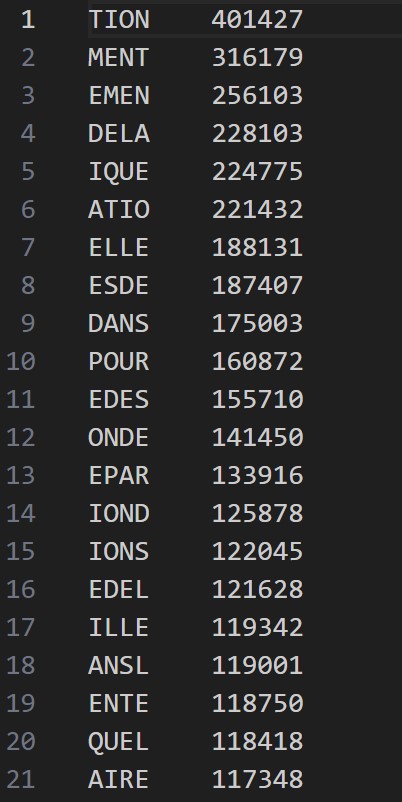
À l’aide d’un fichier contenant les tétragrammes français rangés par ordre décroissant :
La fonction permettant de calculer le score :
On va parcourir le texte de 0 à n-4 afin de couvrir tous les tétragrammes possibles et pour chaque itération, on récupère un tétragramme de 4 lettres à partir de la position précédente.
Pour chaque tétragramme, on va vérifier s'il est présent dans notre fichier (ici, j’ai choisi de mettre les tétragrammes dans un dictionnaire du type {Tétra :Score}). S'il est présent, on ajoute le logarithme naturel de sa fréquence normalisée au score actuel. Sinon, on ajoute le log de 0.01 – le log du nombre total de tétragrammes dans le dictionnaire afin de « pénaliser » et essayer de trouver le maximum de tétragrammes présents dans le dictionnaire.
Pourquoi utiliser le logarithme ?
- La gestion des petites valeurs : Les fréquences des tétragrammes sont souvent des valeurs très petites. Multiplier ces petites valeurs peut rapidement conduire à des problèmes d’imprécision informatique.
- Additivité des probabilités : En travaillant avec les logarithmes des probabilités, on additionne les scores plutôt que de les multiplier, ce qui simplifie les calculs et l'analyse des résultats.
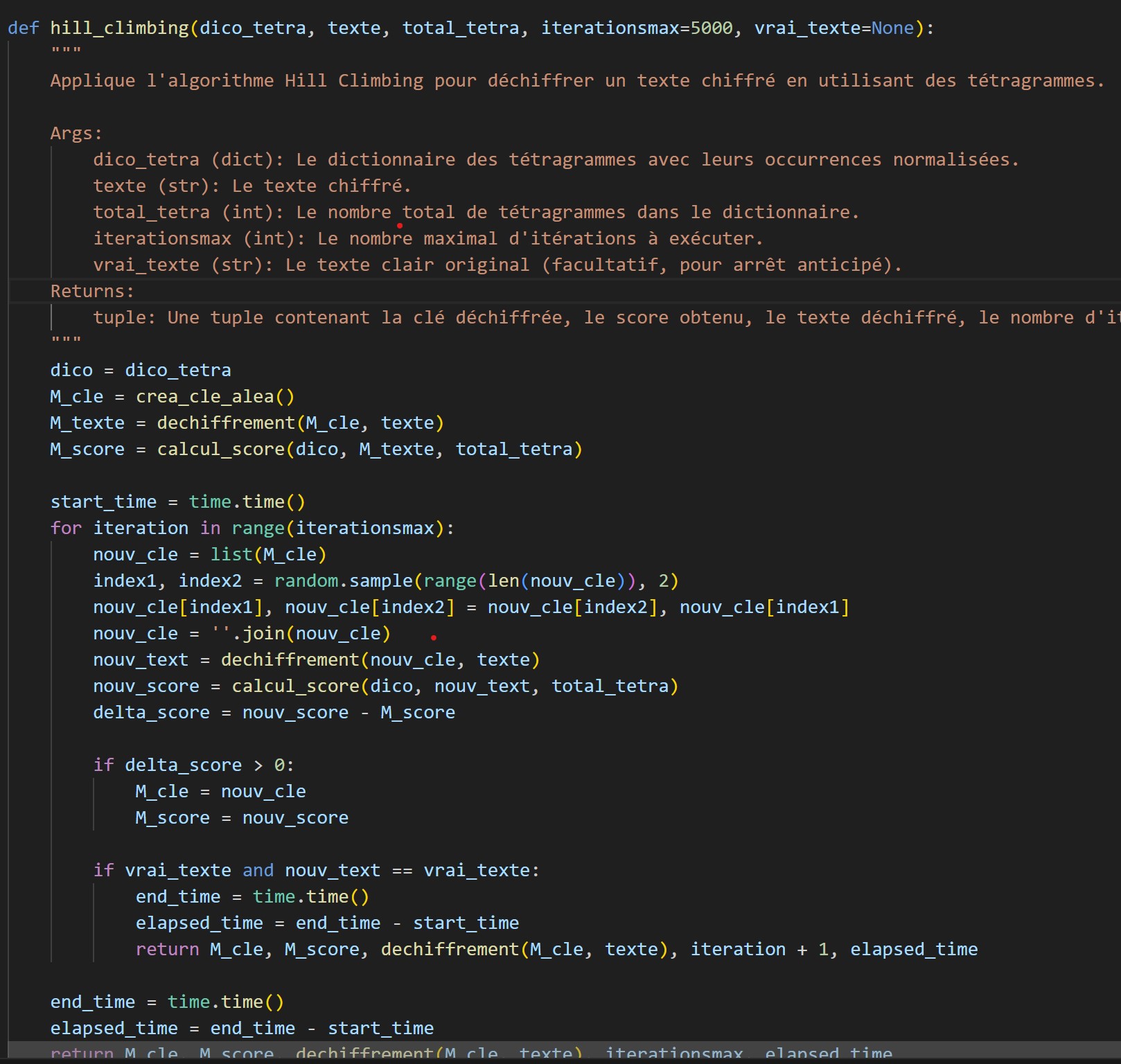
Hill-Climbing Implémentation
Revenons sur le cœur de notre algorithme qui est le Hill-Climbing.
Son implémentation est très simple : on prend une clé aléatoire, on déchiffre le texte chiffré avec, puis on calcule son score. Ensuite, on permute deux lettres de cette clé et on évalue le nouveau score. L’opération est répétée x fois en vérifiant et gardant la meilleure solution à chaque tour.
Si le score est meilleur, la nouvelle clé devient la clé de base et le nouveau score de même. Sinon, on garde les éléments précédents et on permute deux nouvelles lettres.
Tests
Nous n’avons plus qu’à réaliser des tests sur des fichiers de différentes tailles. Chaque test donné à été répété plusieurs fois mais je n'ai garder que l'échantillon le plus globale par soucis de lisibilité
Premier Test
Taille
- 8000 caractères
Amélioration
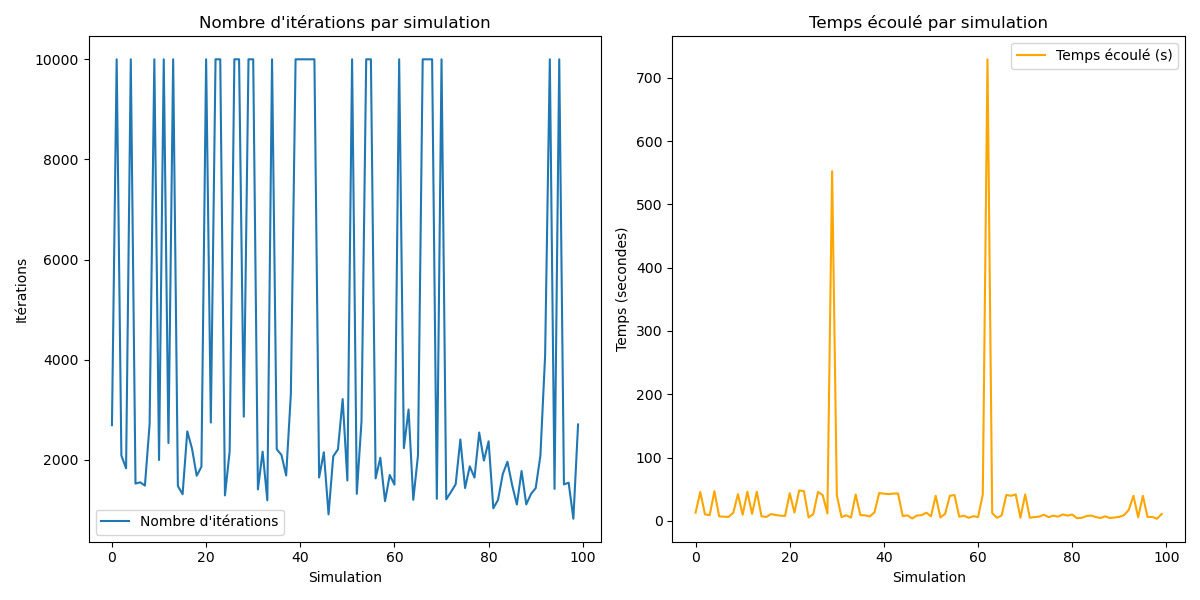
Je donne volontairement le bon texte déchiffré afin d'arrêter la boucle quand on le trouve, ce qui permet de trouver le nombre d'itérations et de temps moyen
Résultat
On voit que le graphique est biaisé par les erreurs car celle-ci on un nombre d'itérations égale à celui de base.
Deuxième Test
Taille
- 8000 caractères
Amélioration
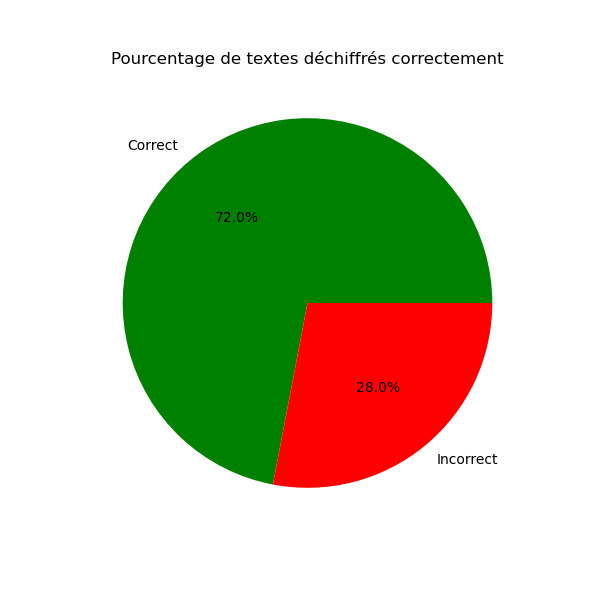
Précédente + Je rajoute le fait d'enlever les tests incorrects dans le graphique
Résultat
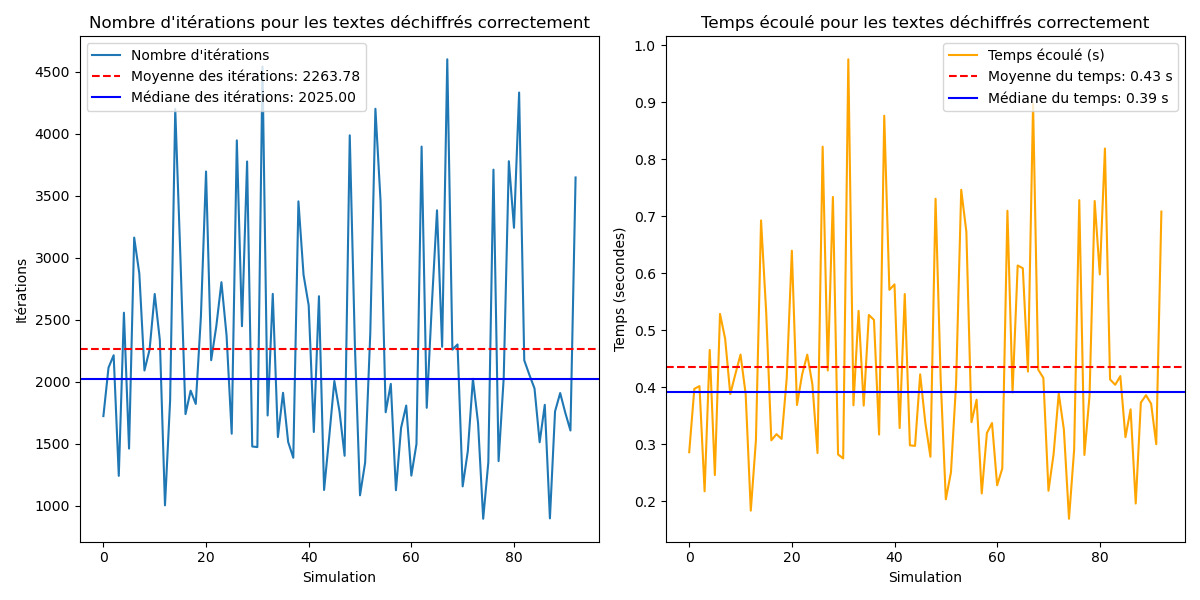
Après une deuxième simulation sur 100 tests, on voit que la moyenne d'itération s'approche des 2000, avec quelques pics vers les 1000 et d'autres a 4000 Le temps lui s'approche des 8,5 sec en moyenne
Troisième Test
Taille
- 4000 caractères
Amélioration
Précédente
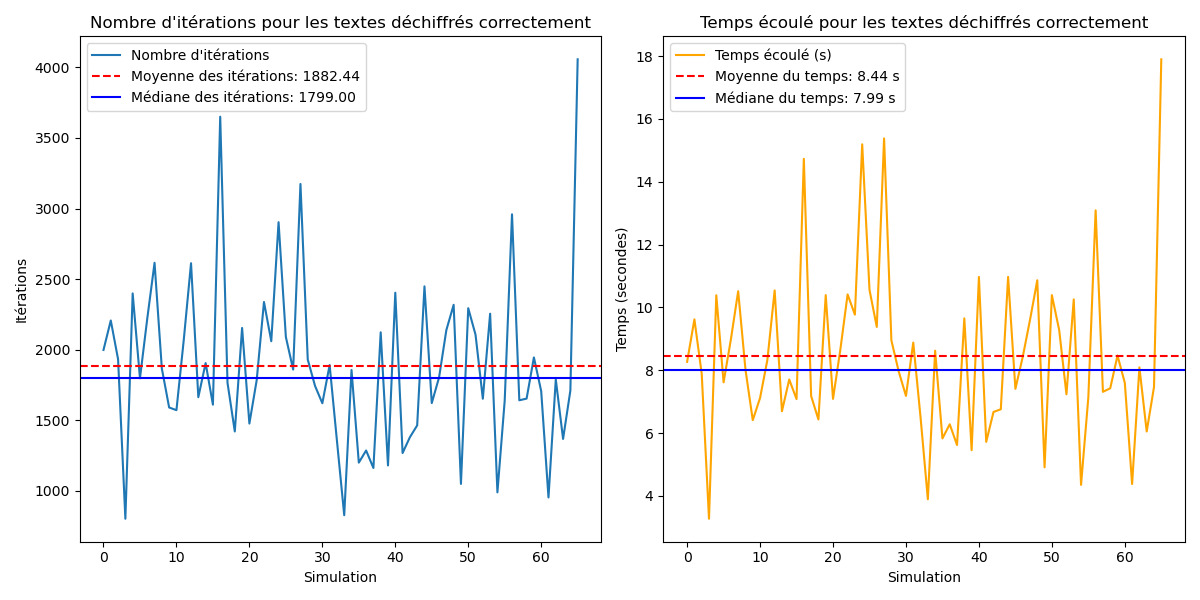
Résultat
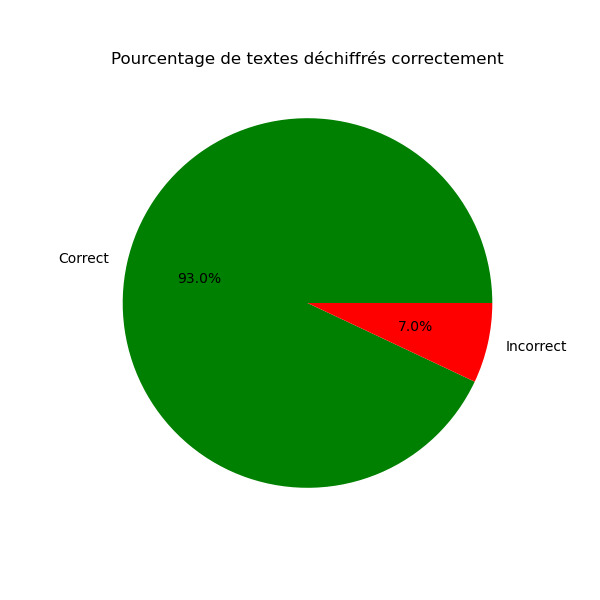
Pour texte deux fois moins long on à un taux de réussite de 93% soit environ 30% de plus que pour le texte de taille double et le temps par itérations est de moins d'une seconde. Cependant la moyenne reste aux alentours des 2000 avec une légère augmentation.
Quatrième Test
Taille
- 1000 mots
Amélioration
Précédente
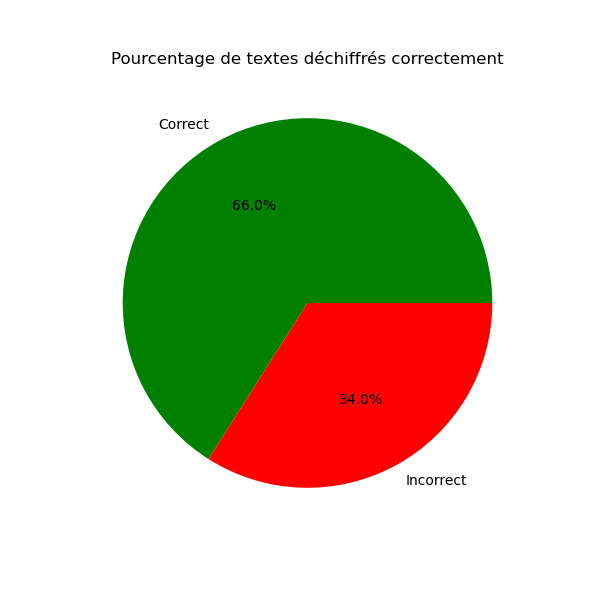
Résultat
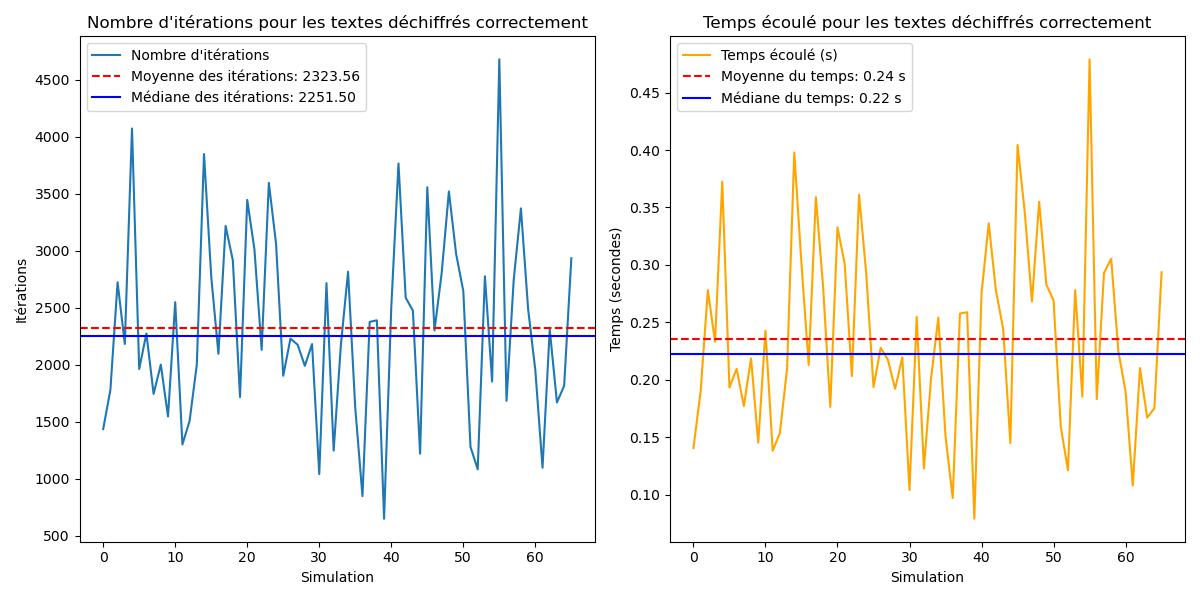
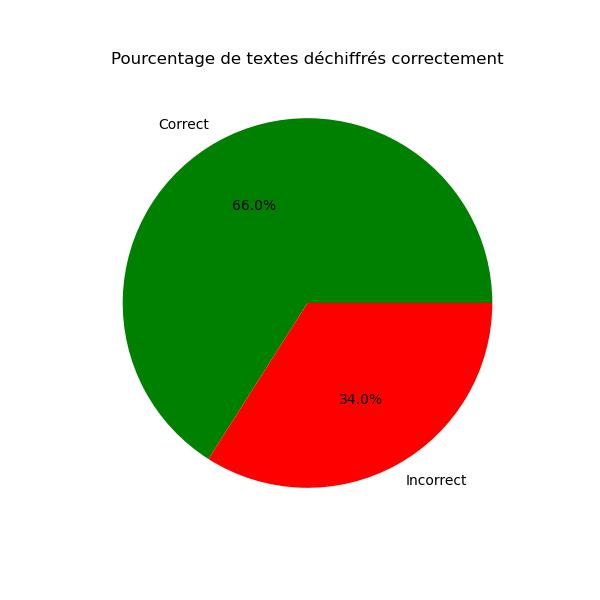
Pour ce texte on à un taux de réussite de 66% ce qui montre quand réduisant trop le texte le pourcentages de réussites des résultats s'amoindrie.
Note
Si la taille de la phrase est inferieure a 100 caractères la moyenne de réussite est très proche de 0%.
Amélioration Globale
Recuit Stimulé
Afin de ne pas interrompre le programme en utilisant le texte original ce qui revient à de la triche on peut utiliser le recuit stimulé qui nous permet de nous sortir des minimums locaux et s'arrêter de manière "légal". Je l'ai programmé mais juste le temps de faire quelques tests qui montrent une baisse temps et un augmentation de réussite pour le texte de taille 8000
(J'approfondirais mes tests dans les jours à venir)