Détection d’anomalies par Isolation Forest : application pour l’industrie 4.0
L'objectif de ce projet était d'étudier et comprendre l'algorithme Isolation Forest afin de pouvoir rédiger un tutoriel d'utilisation.
Qu’est-ce que l’algorithme de détection d’anomalie Isolation Forest et quel est son but ?
En quelques mots l’algorithme Isolation Forest est un algorithme non supervisé de machine learning. Il est conçu pour détecter des valeurs anormales au sein d’un ensemble de données.
En effet de nos jours, beaucoup de données sont collectées grâce aux appareils connectés : voitures, ordinateurs, montres connectées…. Ce développement de l’Internet of things nous impose de savoir collecter et traiter toute ces données de manière optimisée et efficace. Pour cela une des premières étapes après la collecte des données est la détection d’anomalie.
Une anomalie dans un jeu de donnée est une valeur qui dénote des autres, ceci peut être dû à un mauvais fonctionnement d’un capteur ( une température de 10 000 °C dans un four ) ou bien une action qui sors de l’ordinaire à cause de cause extérieurs (un retrait de 3 000 000 $ à un distributeur de billet d’un petit village). Détecter ces anomalies permet de pouvoir identifier un possible disfonctionnement qu’il faudra ignorer dans nos prochains calculs ou bien d’isoler des valeurs que nous allons étudier pour comprendre les causes de leur irrégularités. (par exemple détecter des actes de fraudes dans les paiements en carte de crédit).
Fonctionnement de l’algorithme Isolation Forest
Dataset : Jeu de données en français est un ensemble de données associées, la plupart du temps représenté par un tableau ou un graph.
L’idée principale est de calculer un score d’anomalie pour chaque observation du dataset puis de comparer ces scores dans un second temps pour isoler les anomalies. Ceci est possible car nous nous basons sur l’idée qu’une donnée anormale sera plus facile à isoler qu’une donnée standard dû à son écart (distance par rapport) à ces dernières.
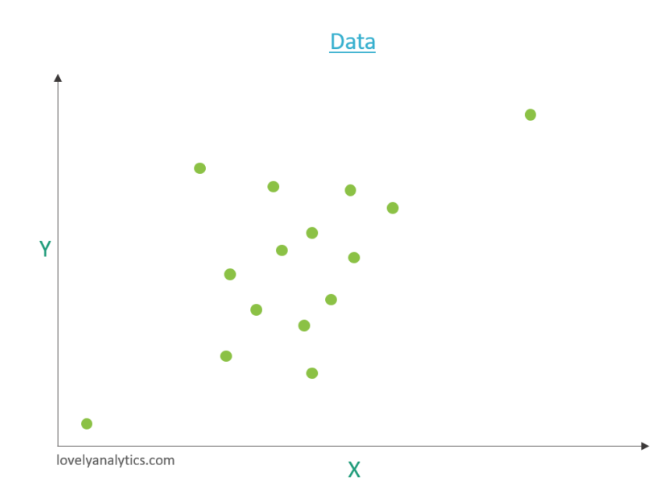
Pour comprendre le fonctionnement de cet algorithme nous allons l’illustrer avec un exemple en 2 dimensions X et Y.
A) La construction d’un arbre
Nous plaçons nos données dans un graphique qui considère Y en fonction de X. Voici à quoi ressemble notre data set dans un premier temps.
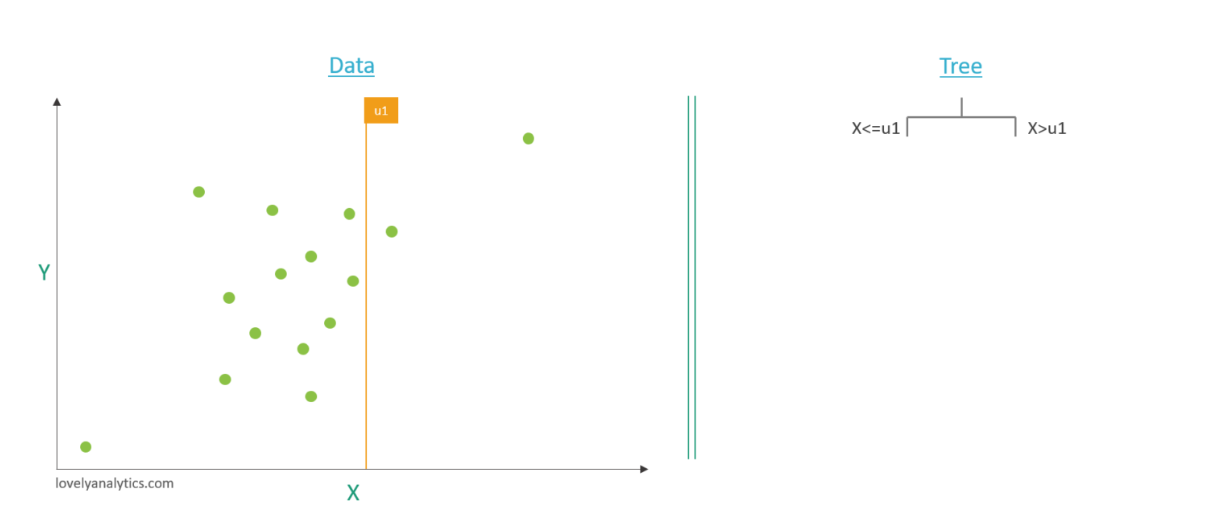
Etape 1 : Sélection d’une variable et d’un seuil
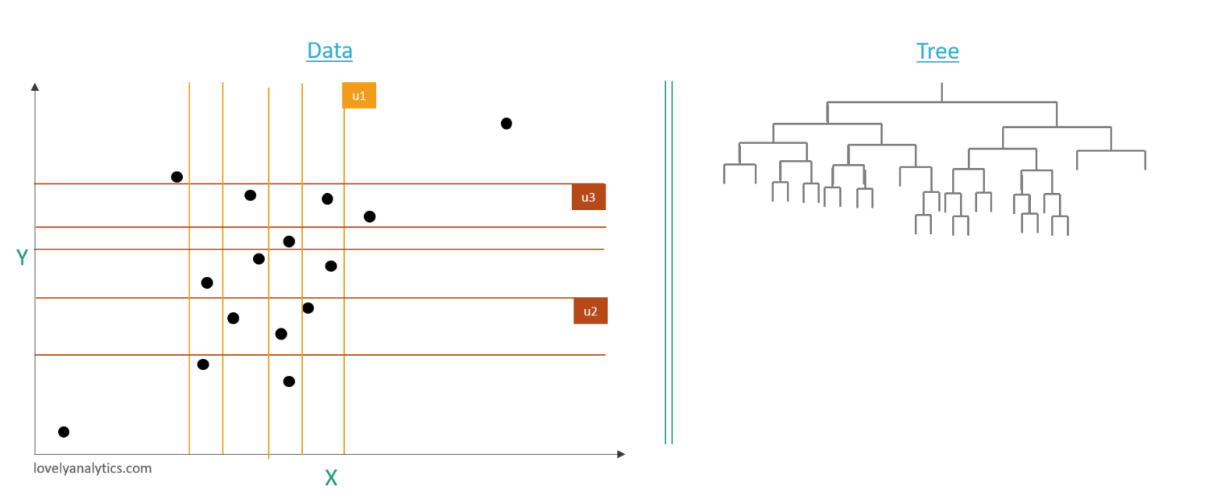
Nous sélectionnons aléatoirement une variable : ici nous avons le choix entre X et Y( mais en réalité bien plus de variables peuvent être prises en compte). Nous repérons les valeurs : - u max qui correspond à la valeur maximale prise par un élément de notre dataset pour cette variable - u min qui correspond à la valeur minimale prise par un élément de notre dataset pour cette variable. Après avoir trouvé cette plage de valeur, un valeur aléatoire de cette dernière est isolée est appelée u1. Nous réalisons alors une découpe (aussi appelée split) de nos données au niveau de u1 et nous commençons donc la création de notre arbres qui va isoler : - à droite : les éléments de notre population qui possèdent pour la variable sélectionnée une valeur inférieur ou égale à u1 - à gauche : les éléments de notre population qui possèdent pour la variable sélectionnée une valeur supérieur à u1
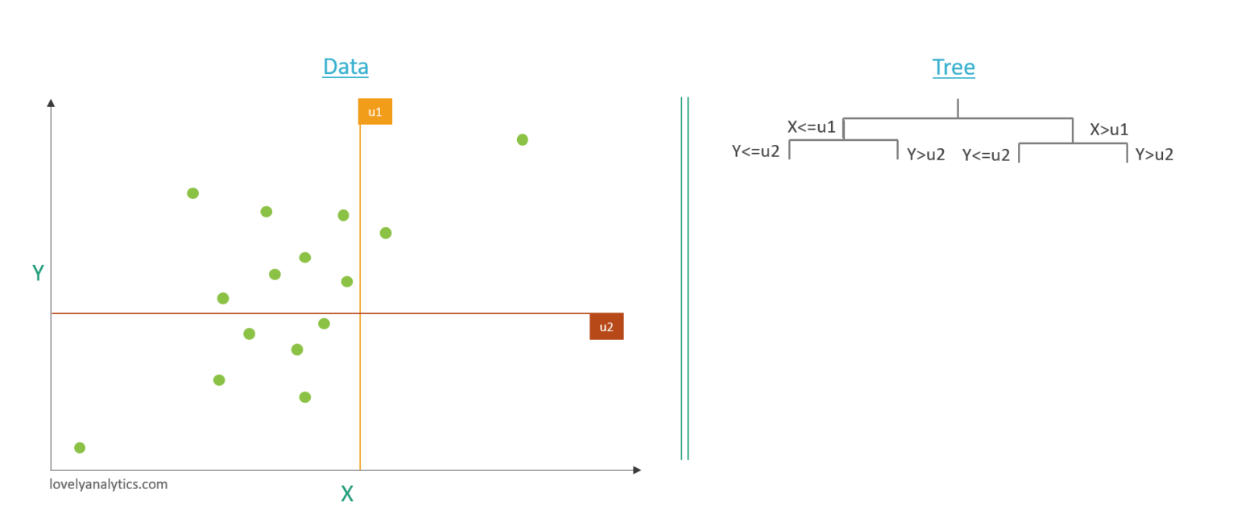
Etape 2 : étape itérative
Nous réitérons l’étape 1 jusqu’à ce que nous ayons un élément « isolé » dans notre arbre. Alors nous créons le seuil U2 dans Y cette fois (aléatoirement) et nous complétons notre arbre.
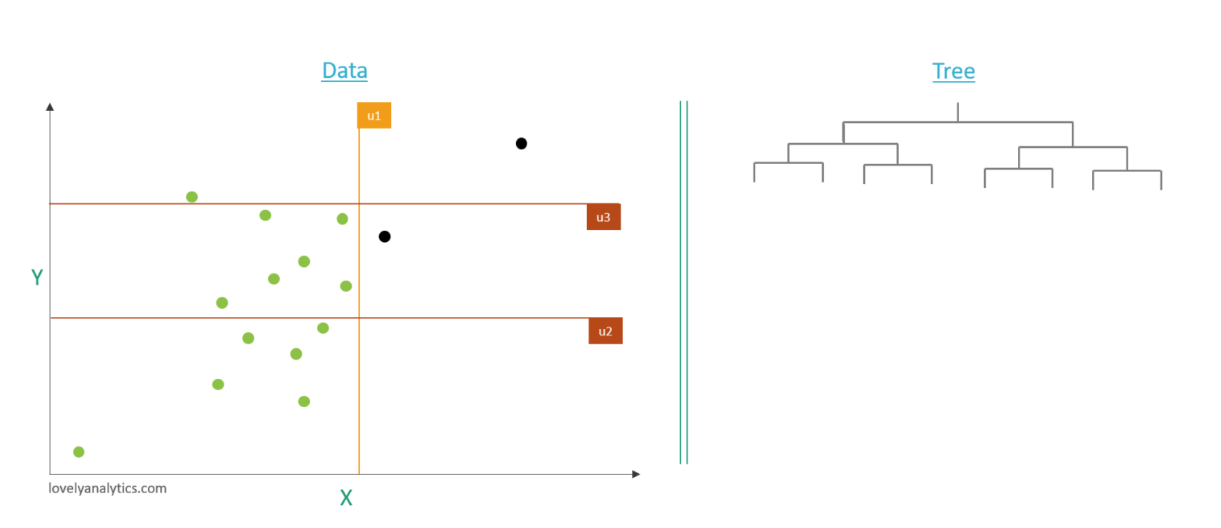
Ainsi de suite jusqu’à l’isolation d’un élément au moins. Dans notre exemple trois étapes suffisent pour isoler les deux points ici mis en noir.
Maintenant que nous avons isolé ces deux points nous les enlevons de notre processus de calcul, autrement dit nous ne les prenons plus en compte dans les calculs de u min et u max et nous continuons d’itérer notre procédure jusqu’à ce que tout les points soient isolés dans une branche de l’arbre. Ici la population est petite il est donc facile de compléter l'arbre jusqu'à ce que tous les éléments soient isolés mais lorsque on traite des populations bien plus imposantes il n'est pas nécessaire de compléter les arbres, on s'arrête usuellement lorsque quelques individus ont étés isolés.
Voici le résultat final dans notre exemple
B) Construction d’une foret
La création d’un seul et unique arbre ne suffit pas pour répondre tout de suite à notre problématique. En effet il est possible d’isoler à tort un éléments suite à des valeurs très spécifiques choisies( par l’aléatoire).
Pour pallier ce risque nous allons relancer le processus avec la même méthode mais avec des sélections de variables et de seuils qui seront forcément différentes étant donné que ces valeurs sont choisies aléatoirement. Nous obtiendrons donc une « forêt » d’arbres que nous allons étudier.
C) Etude de la foret
Maintenant que nous avons créé une foret d’arbres nous allons étudier ces derniers et ce qu’ils nous indiquent sur la population étudiée .
Pour ce faire nous considérons toujours l’idée qu’une valeur atypique est plus facile à isoler autrement dit : plus le nombre de split nécessaire pour isoler une observation particulière est bas plus il y a de chance que cette dernière soit une anomalie.
Nous parcourons donc chaque arbre et nous attribuons à chaque éléments de notre population un score d’isolation. Celui-ci est d’autant proche de 1 que le nombre de split qui a été réalisé pour isolé l’élément est faible. Et il est d’autant proche de 0.5 que le nombre de split qui ont étés réalisés pour isoler l’élément est élevé. Cela correspond à la profondeur de l’arbre qui a mené à ce point
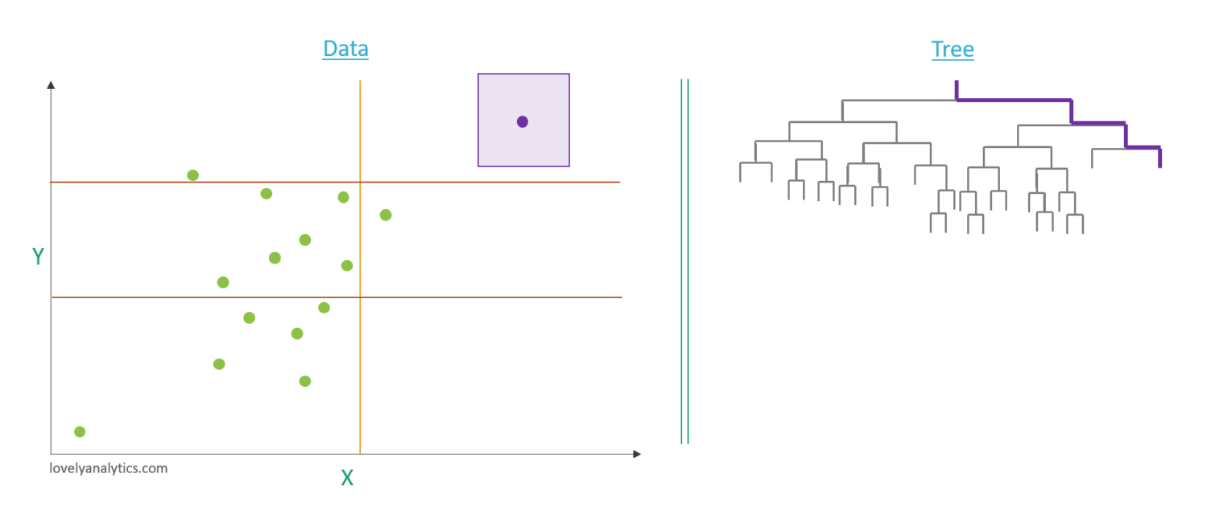
Par exemple pour ce point qui semble anormal il a fallut 3 split pour l’isoler, ce qui est faaible. Son score est donc proche de 1.
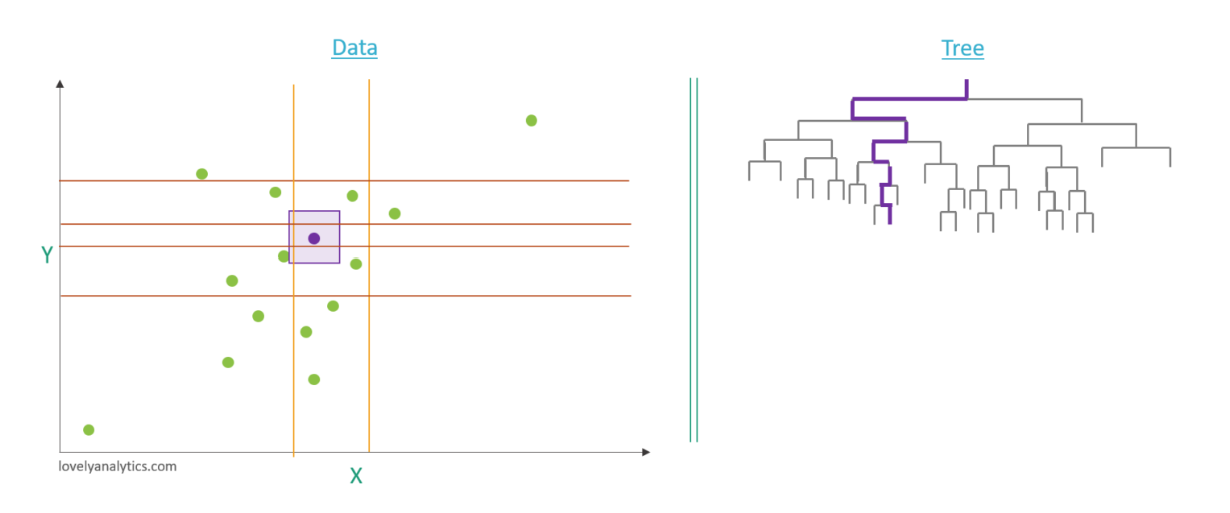
Autre exemple pour ce point qui semble normal il a fallut 7 split pour l’isoler, ce qui est plus élevé. Son score est donc proche de 0,5.
Après avoir relevé les scores de chaque éléments pour chaque arbres de la forêt nous faisons une moyenne pour chaque individu de la population ce qui lui donne un score d’anomalie définitif . Puis nous isolons les éléments qui ont les scores les plus élevés qui sont ceux qui ont le plus de chance d’être atypique. Le nombre d’élément relevé dépend du taux d’anomalie précédemment indiqué.
Résumé du principe
La détection d’anomalie d’erreur se fait en deux grandes étapes :
1. La construction d’iTrees grâce à un ensemble de données d’apprentissage
2. Chaque instance de l’ensemble de test se voit attribuer un score d’anomalie grâce à l’analyse de la foret créée à l’étape précédente
Tuto Code
Un des objectifs de ce projet était de créer un tutoriel permettant à toute personne d'utiliser facilement cet algorithme pour détecter des anomalie dans un dataset donné.
Voir le fichier sur le lien suivant :
Ou la page wiki suivante :
Tutoriel utilisation algorithme Isolation Forest
Les limites de l’algorithme
Cet algorithme fonctionne très bien surtout sur les échantillons qui possèdent « peu » d’éléments ce qui est intéressant étant donné que la plupart des autres méthodes privilégient généralement une grande taille d’échantillonnage. Quelques limites de cette méthode doivent tout de même êtres prises en compte :
- Le masquage : Lorsque le nombre d’anomalies est trop élevé il peut arriver que celles-ci se regroupent dans un groupe dense et grand ce qui rend l’isolation de ces dernières plus difficile. Cela peut donc impacter la détection de ces points comme anomalie.
- L’inondation : si les instances normales sont trop proches des anomalies il est plus fastidieux d’isoler ces dernière ce qui tout comme le masquage impacte la bonne détection d’une anomalie comme telle du à une augmentation de splits nécessaires pour l’isoler.
- Donnés de haute dimension : Cette méthode étant basée sur la distance elle est altérée lorsque les éléments étudiés sont de trop hautes dimensions dû au fait que les points soient clairsemés dans l’espace de dimension élevé.
- Fausses anomalies : D’autre part le système forest prend en paramètre un pourcentage de contamination (déjà limite en soi car il faut déjà avoir une idée du pourcentage de nos anomalies avant de lancé le programme) et ce pourcentage est respecté même si aucune anomalie ou une proportion plus faible d’anomalie est détectée. On entend par la que si 10% d’anomalie ont étés annoncé le programme nous renverra 10% d’anomalies même si tout les scores d’anomalies sont tous très proches et donc qu’aucune différence significative peut être observée entre les éléments du plan.