Dilemme du prisonnier
Introduction
Le dilemme du prisonnier à été inventé en 1950 par Albert William Tucker et fait partie de la théorie des jeux qui est un domaine des mathématiques étudiant les interactions entre différents individus qui sont conscients ou non de ces interactions. Ils devront donc faire des choix dont ils sont conscients ou non lors de ces interactions. Il peut être utilisé pour émettre sur les raisons de certains comportements que l'on observe dans la nature
Le dilemme du prisonnier
Les individus sont soumis dans le dilemme du prisonnier à une interaction où ils ont deux choix : soit ils coopèrent avec l’autre individu, soit ils le trahissent. Les individus sont récompensés selon la matrice des paiements suivante :
L’intérêt de la configuration actuelle de la matrice des paiements est que les individus ont un intérêt certain à trahir l’autre mais la coopération est la meilleure option pour les deux individus. On représente l’intérêt à trahir par rapport à la coopération par la variable B qui dans notre exemple est égale à 1,85.
Afin de simplifier notre modèle nous ne considérerons que deux comportements possibles qui sont :
-Le coopérant qui coopérera systématiquement
-Le traître qui trahira systématiquement
Spatialisation du dilemme du prisonnier
L’idée de spatialiser le dilemme du prisonnier a été présenté par Nowak et May afin de modéliser la diffusion de certains comportements dans des populations en interaction. « The prisoners’ Dilemma is an interesting metaphor for the fundamental biological problem of how cooperative behaviour may evolve and be maintained »(Nowak,M.A. et May, R.M. 1992.Evolutionary games and spatial chaos) Ce model apporte un éclairage mathématique sur des questions liées à l’évolution comme l’apparition de comportements altruistes par exemple ou le maintien de la coopération dans des groupes sociaux. Ce modèle simple peux compléter celui du jeux de la vie (croissance en fonction des ressources) et celui de l’évolution (croisement et sélection) pour expliquer les équilibres écologiques. Nous nous intéresserons donc au équilibres dynamiques produits par notre modèle.
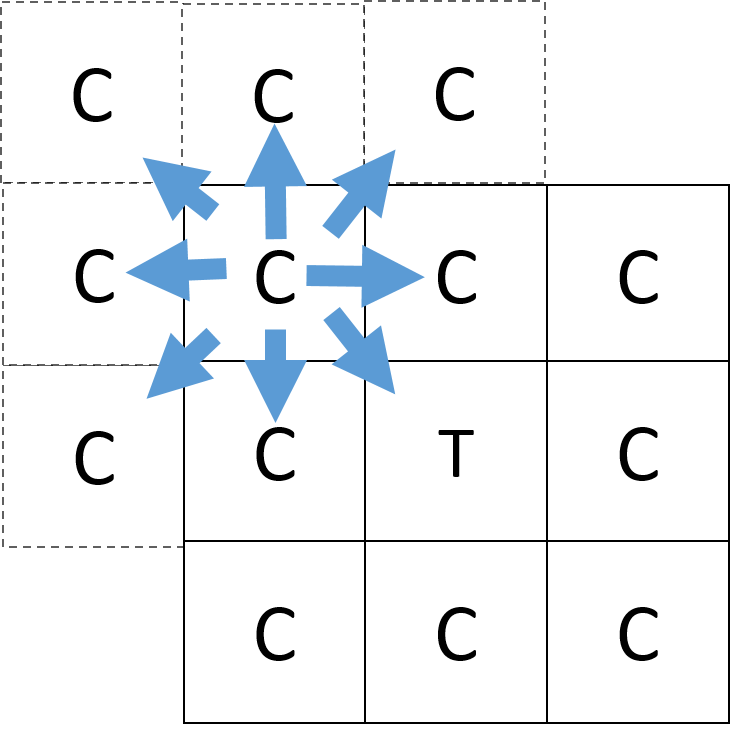
Les prisonniers sont au voisinage de Moore (8 voisins). L’espace dans lequel ils évoluent est un espace toroïdale (bordures ouvertes) en forme de carré de dimension n*n. On peut aussi le représenter comme une matrice carrée avec les bordures qui communiquent entre elles ou un espace en forme de donut. On peut illustrer ces deux règles par l'image suivante qui montre les différents voisins d'un prisonnier sur une bordure de la matrice:
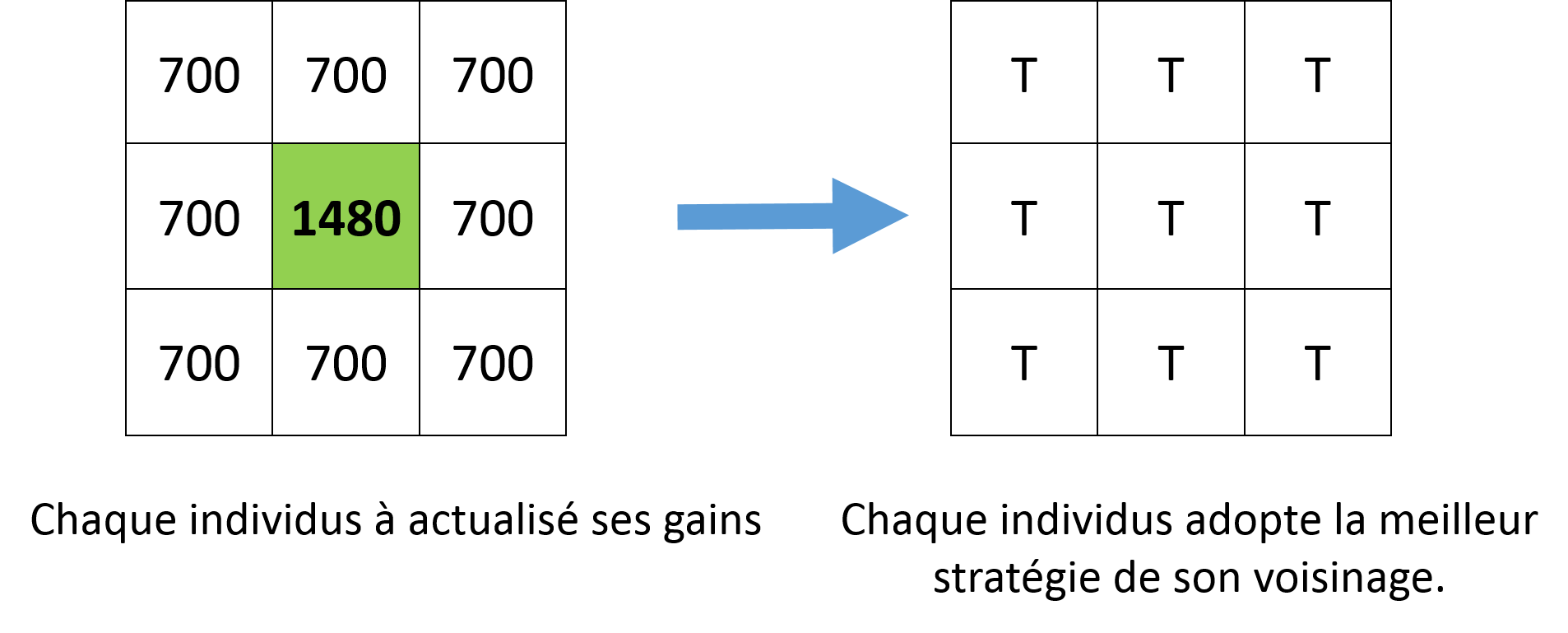
Voici ce qu'il se passe à chaque tour de la simulation pour chaque prisonnier. Pour cette exemple nous allons poser un traître au milieu d'une matrice de 3*3 de coopérants:
Dans les prochaines images on affiche les prisonniers en fonction de leur stratégie actuelle et de leur dernière stratégie. Le code couleur est le suivant :
-en rouge les traîtres qui l’ont été pendant 2 tours consécutifs
-en jaune les coopérants qui sont devenus traîtres
-en vert les traîtres devenus coopérants
-en bleu les coopérants qui l’ont été pendant 2 tours consécutifs
Une expérience intéressante
On propose dans cette partie de commencer à étudier un cas en particulier. Dans cette première expérience nous fixons B à 1,85 et plaçons un traître au milieu de coopérants dans une grille de 301 individus par 301 individus. Nous pensons que cette configuration donnera des résultats intéressants car B n'est pas assez grand pour permettre une domination complète des traîtres ou pas assez petit pour permettre une domination complète des coopérants.
Après quelques tours de la simulation nous observons l'image suivante:
Nous pouvons voir grâce à la bordure verte que le carré de traîtres au centre de l'image est en train de rétrécir alors que dans les coins des îlots de traîtres apparaissent comme nous le montre la grand quantité de jaune.
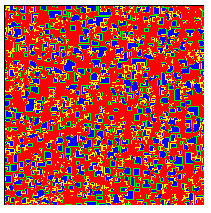
Nous passons sous silence quelques tours pour arriver à la situation suivante:
Nous pouvons voir à présent que les comportements dans la simulation varient beaucoup comme témoignent l'abondance de prisonniers affichés en jaune et en vert.
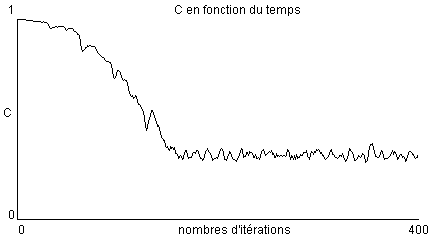
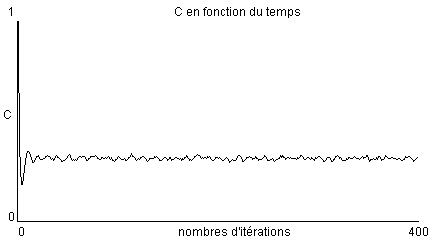
Lors du déroulé de cette simulation nous avons pu récolter C qui est le rapport entre le nombre de coopérants dans la matrice sur le nombre de prisonniers au total. Cette variable nous permettra de visualiser rapidement l'évolution du nombre de coopérants dans la simulation. Nous allons maintenant montrer son évolution au court du temps dans la simulation.
Nous pouvons ainsi observer sur le graphique que C semble tendre vers environ 0.3, montrant de ce fait que la simulation est dominée par les traîtres mais que les coopérants résistent tout de même. Les variations de C ne sont pas cycliques de ce que l'on observe sur le graphique ce qui veut dire que même si le nombre de coopérants semble à peut près stable il n'en reste pas moins fluctuant ou que nous n'avons pas récolté assez de données pour pouvoir affirmer qu'elle est cyclique. On peut supposer que la simulation est cyclique sur x tours( x > 400) mais nous ne pouvons le savoir avec nos données actuelles.
Automatisation des expériences
Nous avons pu observer une simulation particulière mais nous devons maintenant pouvoir faire des observations autres que visuelles car nous n’avons pas le temps de le faire pour toutes les expériences permises par notre modèle. Nous n’as alors décidé de créer un objet dans le programme pour extraire les données des expériences et nous les résumer. Nous ne montrerons toutefois que les expériences que l’on juge intéressantes.
Nous voulons tout d'abord mesurer l'influence de B sur l'évolution d'une répartition aléatoire. Pour cela nous fixerons les paramètres suivants pour chaque simulation. Dans chaque simulation on aura systématiquement 10% de traîtres répartis aléatoirement parmi 90% de coopérants. La dimension des matrices sera de 200*200. Nous ferons variez B entre 1.75 et 2.
Pour un B appartenant à [1.75;1.8[ On observe la simulation suivante au bout de 400 tours:
On observe des réseaux de traîtres interconnectés entre eux mais pouvant être indépendants avec une taille minimale d'un carré de 4 traîtres. On observe aussi des zones ou les prisonniers alternent entre traître et coopérant, on les repère en cherchant les zones en jaune ou en vert.
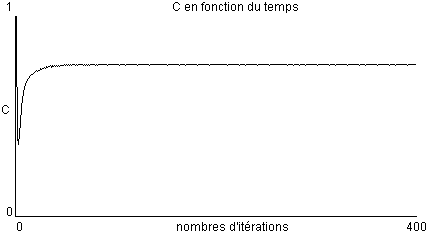
Le graphique de l'évolution de C est le suivant:
Ce graphique nous permet d'affirmer que la simulation est à peut près stable car on observe toujours des petits chutes du nombre de coopérants. C semble tendre par ailleurs vers 0.7.
Pour un B appartenant à [1.8;2[ On observe la simulation suivante au bout de 400 tours:
On observe une situation chaotique avec une majorité de traîtres et des îlots de coopérants apparaissant et disparaissant au fur et à mesure de la simulation. On remarque aussi beaucoup de jaune et de vert sur les images, cela nous montre que les comportements des prisonniers changent beaucoup.
Le graphique de l'évolution de C est le suivant:
Ce graphique nous montre que la simulation n'est pas stable mais que C se stabilise vers 0.3.
Il est aussi à noter que sur les images B est à 1.9 et que plus B tend vers 1.8, plus C se stabilise vers 0.4.
Pour un B supérieur à 2 On observe la simulation suivante au bout de 400 tours:
On observe que les traîtres occupent quasiment tout l'espace et que les coopérants sont regroupés en îlots qui s'étendent et se rétrécissent périodiquement.
Le graphique de l'évolution de C est le suivant:
Ce graphique nous montre que la simulation est très stable et que C tend vers 0.02.
Améliorations à apporter
Nous n’avons pas exploré toutes les possibilités de notre modèle. Nous discuterons ici des améliorations à apporter à notre modèle.
La première des améliorations que nous pourrions apporter pourrait être l’introduction de comportements avec un historique des actions passées de leurs voisins. Cela nous permettrait d’avoir des stratégies plus complexes à étudier.
La deuxième amélioration que nous pourrions apporter serait une amélioration au niveau du code. On proposerait de faire en sorte d’avoir un objet Stratégie qui se passerait de prisonnier en prisonnier. Grâce à la programmation objet on pourrait créer des Stratégies variées avec peu de changement dans la structure du programme.
Conclusion
Dans toutes les expériences que nous avons pu réaliser les traîtres n'ont jamais conquis l’entièreté de la matrice. Nos simulations tendent toujours vers un équilibre où les traîtres et les coopérants ont leur place. Ceci peut expliquer en partie pourquoi les comportements coopératifs semblent toujours persister dans la nature alors même que les individus ont plus intérêt à ne pas coopérer. Toutefois notre modèle n'en reste pas moins une abstraction de la réalité et donc ne peut pas expliquer l'intégralité des comportements que l'on retrouve dans la nature et pourrait même être erroné.
Code Source
Comme notre code source est d'une longueur d'environ 1800 lignes on ne le mettra pas dans cette page web. Nous proposons néanmoins de le retrouver à l'adresse suivante