Ensemble de Mandelbrot et autres fractales
Ce projet a été réalisé en Python sur un notebook Jupyter.
Qu'est ce que l'ensemble de Mandelbrot ?
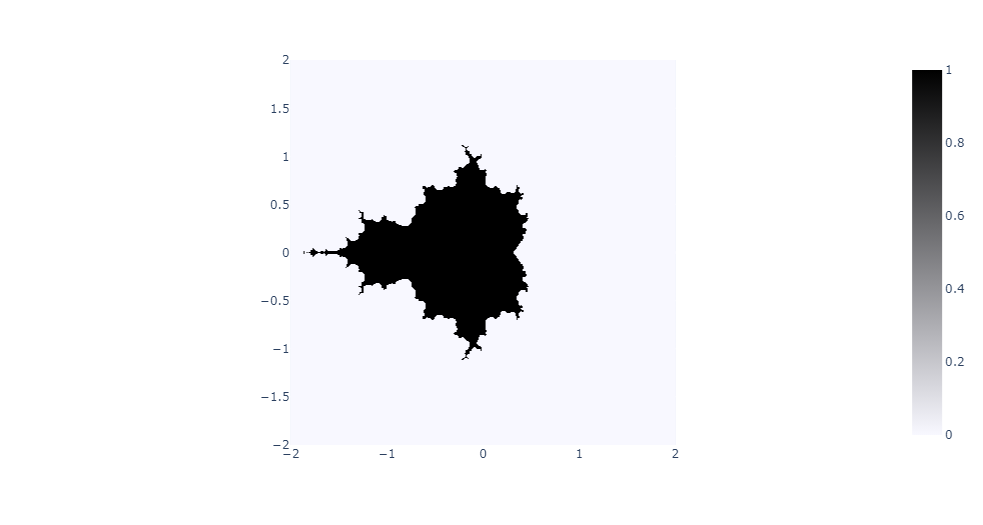
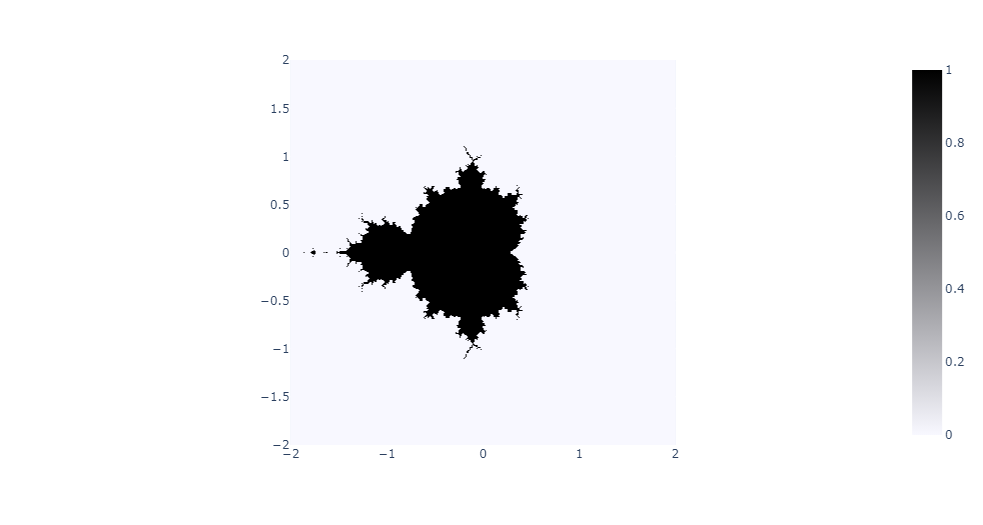
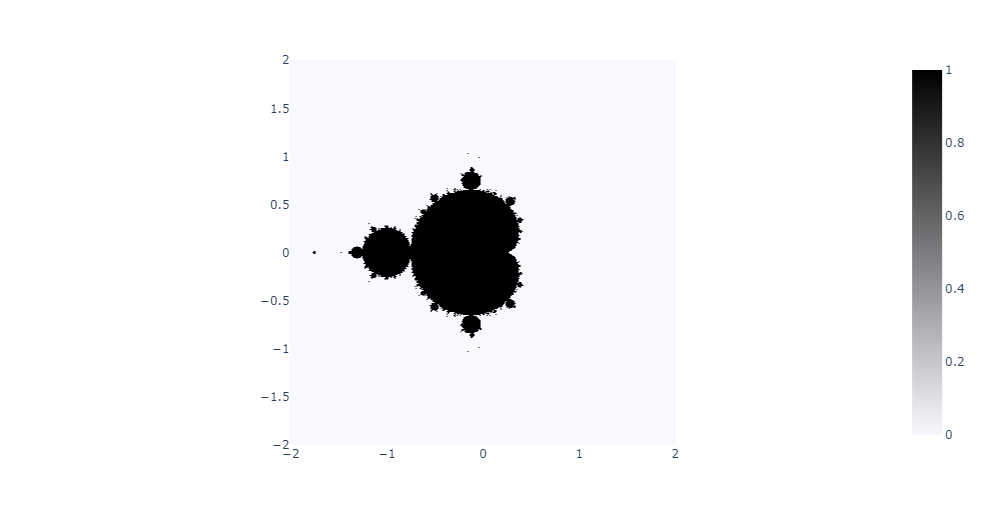
L'ensemble de Mandelbrot est une fractale, c'est-à-dire une figure mathématique identique à toutes les échelles. Cet ensemble fut découvert par Gaston Julia et Pierre Fatou avant la Première Guerre Mondiale. Son nom vient du mathématicien polono-franco-américain Benoît Mandelbrot, qui réalisa les premières représentations de l'ensemble dans les années 1980. Les différents points de l'ensemble correspondent aux points des ensembles de Julia connexes, qui sont des ensembles différents pour chaque point du plan complexe.
L'ensemble de Mandelbrot est régi par une formule mathématique simple : zn+1 = zn * zn + c, où zn est un nombre complexe évoluant avec le temps et c un point complexe constant. Pour savoir si un point appartient à l'ensemble de Mandelbrot ou non, on répète ce calcul un certain nombre de fois, puis on calcule le module du point complexe obtenu. S'il est strictement inférieur à 2, le point appartient à l'ensemble. Au début du calcul pour un point complexe donnée, zn et c sont égaux.
Programme naïf en python
Le programme dit "naïf" est un programme qui est le plus "évident" possible, c'est-à-dire sans optimisations.
def intervalle(min, max, nbInter):
"""Renvoie des tableaux contenant des valeurs pour x et y
En entrée : min et max, les limites de l'espace et nbInter, le nombre de découpages voulus sur l'intervalle min-max
En sortie : deux tableaux, tabx et taby, contenant les différentes valeurs de x et y selon le découpage"""
inter = (max-min)/(nbInter-1)
tab = [min]*(nbInter)
for i in range (0,nbInter):
tab[i] = min + (inter*i)
return tab
Ici, on calcule un tableau qui sert pour les axes du graphe ainsi qu'au calcul des différents points du plan complexe.
def Mandelbrot(x,y,nbIteration,ModuleMax):
"""Indique si un nombre complexe fait partie de l'ensemble de Mandelbrot ou non
En entrée : x et y, deux coordonées, nbIteration, le nombre de répétitions de la formule et ModuleMax, le module à ne pas dépasser
En sortie : un entier, indiquant si le complexe appartient à l'ensemble ou non """
nombre = x+(y*1j)
i = 1
z = nombre
c = nombre
appartient = True
while i <= nbIteration and appartient==True :
if abs(z)>ModuleMax :
appartient = False
z = (z*z)+c
i += 1
return int(appartient)
Cette fonction est la fonction de calcul des points. Pour un nombre d'itérations donné et un module maximum à ne pas dépasser, la fonction se répète et retourne le nombre d'itérations qu'il a fallu pour que le module du nombre complexe dépasse le ModuleMax. Si le nombre d'itérations obtenu est égal au nombre d'itérations donné en paramètre, le point complexe fait partie de l'ensemble.
def ensembleMandelbrot(Xmin,Xmax,Ymin,Ymax,largeur,hauteur,nbIteration,ModuleMax):
"""Retourne le tableau permettant d'afficher l'ensemble de Mandelbrot
En entrée : min et max, les bornes, nbInter, le nombre de découpages voulus, nbIteration, le nombre de répétitions et ModuleMax, le module à ne pas dépasser
En sortie : trois tableaux, le tableau des x, le tableau des y, et le tableau d'affichage de l'ensemble de Mandelbrot"""
tabx = intervalle(Xmin,Xmax,largeur)
taby = intervalle(Ymin,Ymax,hauteur)
img_nb = [[0]*len(taby) for i in range (len(tabx))]
for j in range (len(taby)):
for i in range (len(tabx)):
img_nb[len(tabx)-1-j][i] = Mandelbrot(tabx[i],taby[j],nbIteration,ModuleMax)
return (tabx, taby, img_nb)
Ceci est la fonction principale, celle qui automatise tout le processus. A chaque tour de boucle, un point complexe est sélectionné avec les tableaux de coordonnées x et y. Ce point est soumis à la fonction de calcul et le nombre d'itérations qui en ressort est stocké dans un tableau qui servira à l'affichage. A la fin de la fonction, on retourne les tableaux de coordonnées x et y, ainsi que le tableau des itérations img_nb.
def afficheMandelbrot(tab,tab2,tab3):
fig = px.imshow(tab,origin="lower",color_continuous_scale=["#F8F8FF","#000000"],x=tab2,y=tab3)
fig.show()
Enfin cette fonction permet d'afficher l'ensemble de Mandelbrot avec la bibliothèque plotly. On fournit d'abord le tableau correspondant aux différents points calculés, l'origine du repère, les deux couleurs (blanc et noir), ainsi que les axes avec les tableaux de coordonnées x et y.
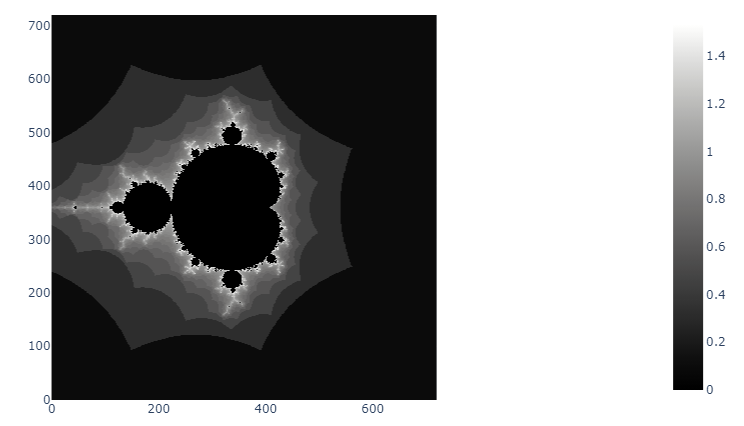
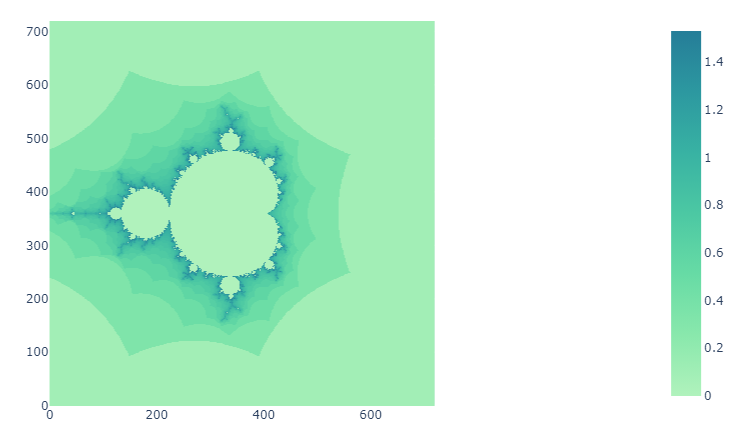
Dans les exemples ci-dessous, les paramètres utilisés sont un ModuleMax de 2, ainsi que X et Y variant sur l'intervalle [-2;2].
Optimisations
Il existe divers moyens d'optimiser l'ensemble de Mandelbrot, mais principalement au niveau du nombre de calculs ou modifier la manière dont les calculs sont faits.
Explications
Symétrie sur l'axe des réels
Il faut savoir que l'ensemble de Mandelbrot est une fractale symétrique selon l'axe des réels. De ce fait, on peut donc diviser le temps total de calcul par 2, puisqu'il suffit de calculer une moitié et de faire son symétrique par rapport à l'axe des réels. L'optimisation apportée se trouve alors dans la fonction ensembleMandelbrot, qui centralise tout. Après modification, on obtient :
img_nb1 = [[0]*len(taby) for i in range (len(tabx))]
for j in range (len(taby)//2):
for i in range (len(tabx)):
img_nb1[-1-j][i] = Mandelbrot(tabx[i],taby[j],nbIteration,noOpti)
img_nb1[j][i] = img_nb1[-1-j][i]
Dans les deux dernières lignes on assigne par symétrie les points déjà calculés.
Calculs
La seconde optimisation dont on peut parler concerne la fonction Mandelbrot, qui calcule la divergence d'un point complexe. Dans la version "naïf", on vérifie à chaque tour de boucle si le module du nombre complexe est inférieur au ModuleMax. On peut tout d'abord fixer le ModuleMax à 2, qui est la valeur reconnue pour l'ensemble. Enfin, le calcul peut être modifié de différentes manières. La première est de vérifier si l'addition de la partie réelle et de la partie imaginaire est strictement inférieure à 4 : cela revient à mettre l'équation d'avant, abs(z) < 2, au carré. Ce qui donne z.real*z.real + z.imag*z.imag < 4. On peut également changer à nouveau cette inégalité en séparant l'inégalité en deux : z.real2 < 2 et z.imag2 < 2. Avec les optimisations de calcul, on peut passer de 5 opérations par tour de boucle à seulement 3. Ce qui peut donner la fonction suivante.
def Mandelbrot(x,y,nbIteration,noOpti):
"""Indique si un nombre complexe fait partie de l'ensemble de Mandelbrot ou non
En entrée : x et y, deux coordonées, nbIteration, le nombre de répétitions de la formule et ModuleMax, le module à ne pas dépasser
En sortie : un entier, indiquant si le complexe appartient à l'ensemble ou non """
nombre = complex(x,y)
z= nombre
c=nombre
x0 =x
y0 =y
x2 = 0
y2 = 0
i = 1
appartient = True
while i<=nbIteration and appartient == True:
if noOpti == 1:
if abs(z.real)>2 or abs(z.imag)>2 :
appartient = False
z = z*z+c
if noOpti == 2:
if x2+y2 >= 4 :
appartient = False
y = (x+x)*y+y0
x = x2-y2+x0
x2 = x*x
y2 = y*y
i += 1
if appartient==True :
return 0
else :
return log(log(i))
Le double logarithme sur le nombre d'itérations permet d'utiliser une des palettes de couleurs de plotly.
On peut également optimiser la manière de calculer les points et non les opérations.
Boundary tracing
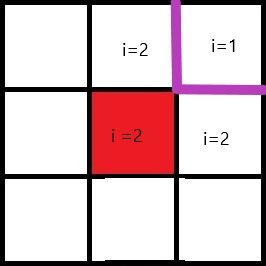
Le boundary tracing consiste à prendre un point et regarder ses voisins pour voir quelle est leur divergence et ainsi tracer une frontière.
Si on prend le pixel rouge dans la figure 1, la fonction va aller chercher dans sa mémoire les divergences des différents voisins, indiquées par le i de ce pixel et ainsi dessiner une frontière comme dans la figure 2. La fonction suivante suit ce principe. On initialise trois tableaux : Todo, Mem et Done, qui sont respectivement le tableau des pxiels restants, les données des pixels calculés et les pixels calculés. A chaque tour de boucle, plusieurs conditions vont être vérifiées pour un point et c'est le résultat de ces conditions qui permettra de dessiner les "frontières de divergence". Cette méthode a cependant un coût : elle doit garder en mémoire des informations sur les différents pixels tout le long de l'exécution.
def mandelbrot_boundary_tracing(tabx, taby, max_iter,noOpti):
"""Permet de réaliser l'ensemble de Mandelbrot en utilisant les frontières"""
grid_size = len(tabx)
Todo = set()
for i in range(grid_size):
Todo.add((i, 0))
Todo.add((i, grid_size-1))
for i in range(grid_size):
Todo.add((0, i))
Todo.add((grid_size-1, i))
Mem = [[-1 for _ in range(grid_size)] for _ in range(grid_size)]
Done = [[False for _ in range(grid_size)] for _ in range(grid_size)]
def value(i, j):
n = Mem[j][i]
if n >= 0:
return n
n = compute(i, j)
Mem[j][i] = n
return n
def compute(i, j):
n = Mandelbrot(tabx[i], taby[j], max_iter,noOpti)
#print(i,j)
return n
while Todo:
i, j = Todo.pop()
c = value(i, j)
Done[i][j] = True
if i > 0:
cc = value(i-1, j)
if cc != c and not Done[i-1][j]:
Todo.add((i-1, j))
if i < grid_size-1:
cc = value(i+1, j)
if cc != c and not Done[i+1][j]:
Todo.add((i+1, j))
if j > 0:
cc = value(i, j-1)
if cc != c and not Done[i][j-1]:
Todo.add((i, j-1))
if j < grid_size-1:
cc = value(i, j+1)
if cc != c and not Done[i][j+1]:
Todo.add((i, j+1))
if i > 0 and j > 0:
cc = value(i-1, j-1)
if cc != c and not Done[i-1][j-1]:
Todo.add((i-1, j-1))
if i < grid_size-1 and j > 0:
cc = value(i+1, j-1)
if cc != c and not Done[i+1][j-1]:
Todo.add((i+1, j-1))
if i > 0 and j < grid_size-1:
cc = value(i-1, j+1)
if cc != c and not Done[i-1][j+1]:
Todo.add((i-1, j+1))
if i < grid_size-1 and j < grid_size-1:
cc = value(i+1, j+1)
if cc != c and not Done[i+1][j+1]:
Todo.add((i+1, j+1))
return Mem
Periodicity checking
Cette méthode permet de vérifier si un point obtenu par itération d'un pixel a été obtenu avant, et si c'est le cas, le point ne peut pas diverger et fait partie de l'ensemble. Comme la méthode "boundary tracing" vue juste au-dessus, la fonction doit également stocker des informations et les conserver tout du long de son exécution.
Cela nous amène au code qui suit :
def peridocity(précision, x,y,max_iteration):
xold = 0
yold = 0
period = 0
iteration = 0
while (x*x + y*y <= 2*2 and iteration < max_iteration) :
xtemp = x*x -y*y + x
y = 2*x*x +y
x = xtemp
if abs(x-xold) < précision and abs(y-yold) < précision:
iteration = max_iteration
period += 1
if period > 20 :
period = 0
xold = x
yold = y
iteration += 1
return i
Le paramètre "précision" sert dans la comparaison entre le point obtenu et ceux en mémoire. Il agit comme une tolérance.
Comparaison des optimisations
Les différents temps relevés ci-dessous ont été mesurés avec la bibliothèque time de python. Il est important de préciser que les temps peuvent varier selon les différents processus actifs au moment du chronométrage. Tous les temps ont donc été mesurés en "même temps", c'est-à-dire sans que d'autres processus soient lancés avant, pendant ou après les chronométrages.
Ce premier tableau compare la vitesse de calcul pour une partie d'ensemble de hauteur 720 pixels et de largeur 720 pixels, gradué de -2 à 2 sur l'axe des réels et des imaginaires purs. On voit que la comparaison individuelle des composants réel et imaginaire du nombre complexe z est légèrement plus rapide que les deux autres méthodes.
| Opération effectuée lors du calcul du point | z.imag() < 2 and z.real() < 2 | ||
| Temps (en secondes) | |||
| Temps 1 | 2.716234 | 2.642379 | 2.351368 |
| Temps 2 | 2.666292 | 2.653635 | 2.322908 |
| Temps 3 | 2.625311 | 2.681878 | 2.331959 |
| Temps 4 | 2.642752 | 2.628538 | 2.329314 |
| Temps 5 | 2.638467 | 2.643233 | 2.300474 |
| Temps moyen | 2.656611 | 2.649933 | 2.327205 |
Le code qui suit correspond aux opérations effectuées quand la manière "Classique" : Réduction du nombre de multiplications est choisie. Le booléen "appartient" permet d'arrêter la boucle while de calcul. Les variables x et y correspondent aux coordonnées du point en cours de calcul.
if x2+y2 >= 4 :
appartient = False
y = (x+x)*y+y0
x = x2-y2+x0
x2 = x*x
y2 = y*y
Ci-dessous, nous avons le même tableau comparatif qu'au-dessus, mais appliqué cette fois aux manières d'effectuer le calcul du point. Dans mon programme, elles sont au nombre de 4 : boundary tracing (utilisation des "frontières" de divergence), periodicity checking, comparaison individuelle des composantes du nombre complexe et réduction du nombre de multiplications (avec le code au-dessus). On remarque que la méthode du boundary tracing permet de gagner 1 seconde environ par rapport aux autres méthodes.
| Manière d'effectuer le calcul du point | Boundary tracing | Periodicity checking | "Classique" : abs(z.real) < 2 and abs(z.imag) < 2 | "Classique" : Réduction du nombre de multiplications |
| Temps (en secondes) | ||||
| Temps 1 | 1.408427 | 2.132469 | 2.652909 | 2.478800 |
| Temps 2 | 1.334971 | 2.112017 | 2.579431 | 2349646 |
| Temps 3 | 1.354671 | 2.169552 | 2.582812 | 2.319928 |
| Temps 4 | 1.349450 | 2.128148 | 2.600136 | 2.364119 |
| Temps 5 | 1.356400 | 2.107562 | 2.616221 | 2.334971 |
| Temps moyen | 1.3607838 | 2.1339496 | 2.6063018 | 2.369428 |
Programme
Ce lien mène vers mon programme avec les différentes optimisations listées dans les sections précédentes. Programme optimisé
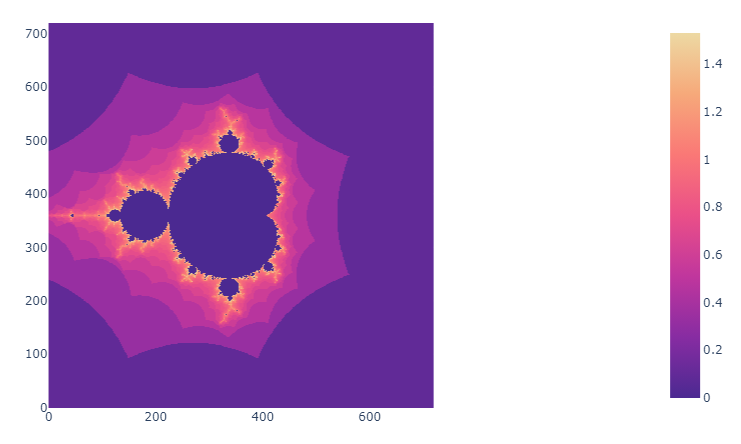
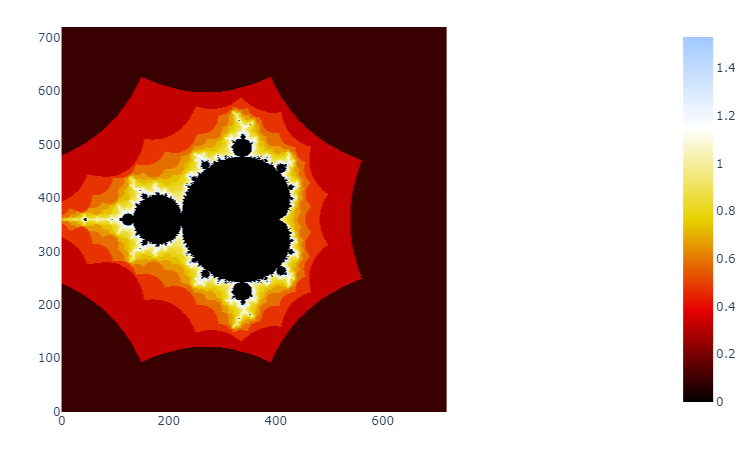
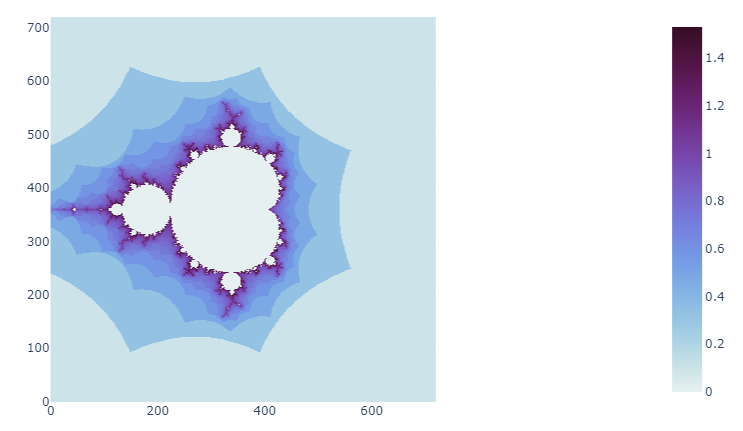
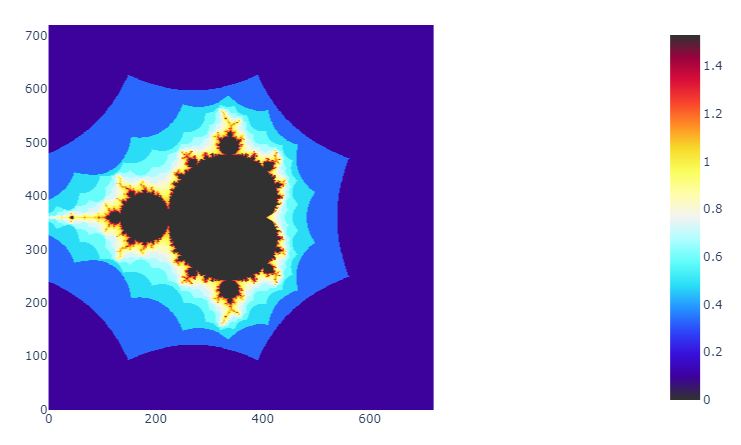
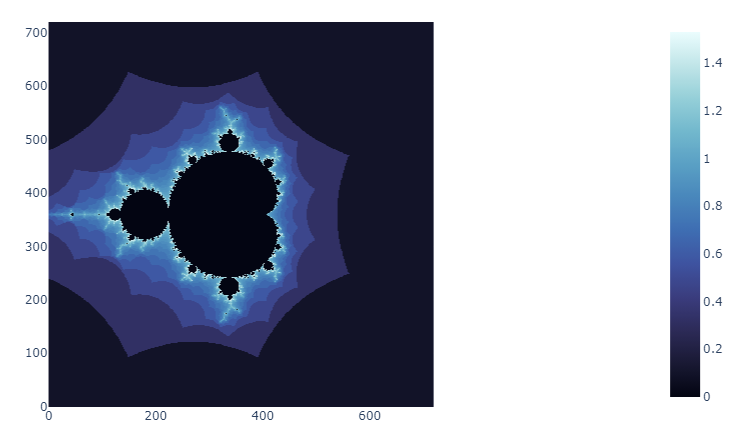
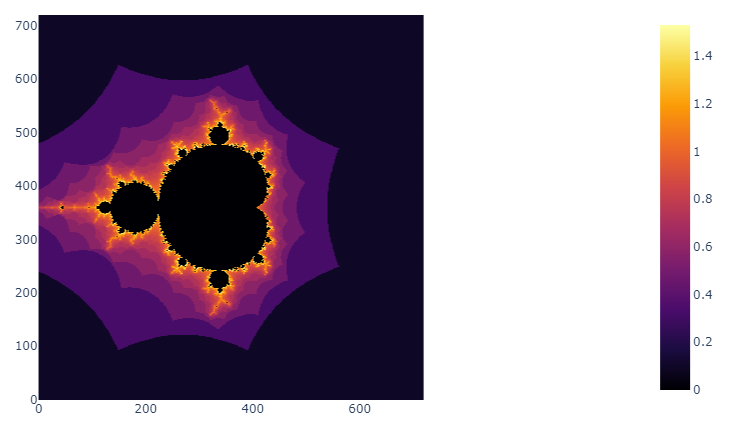
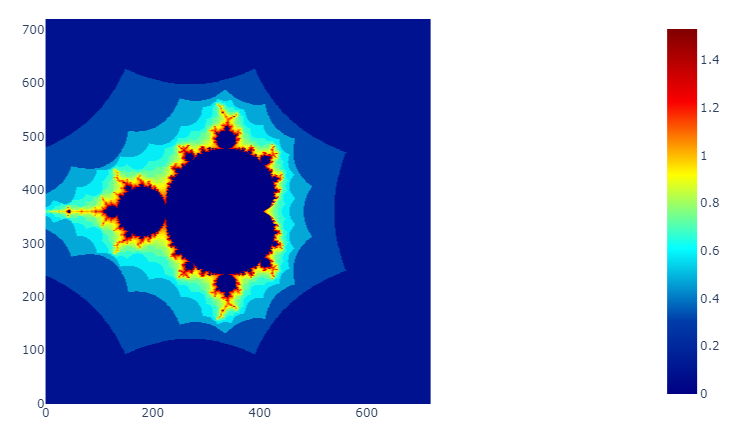
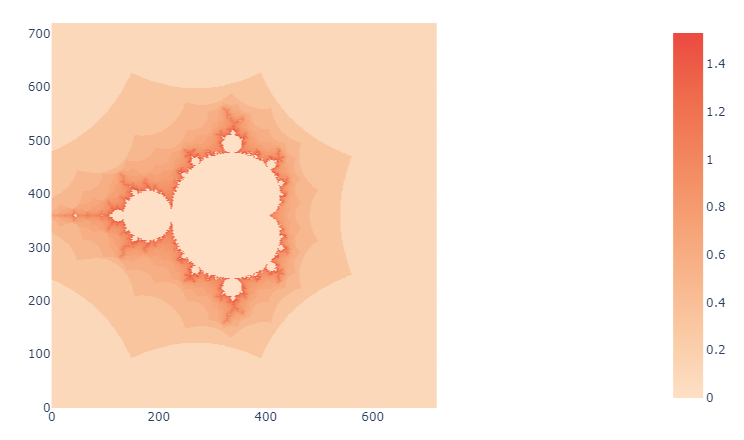
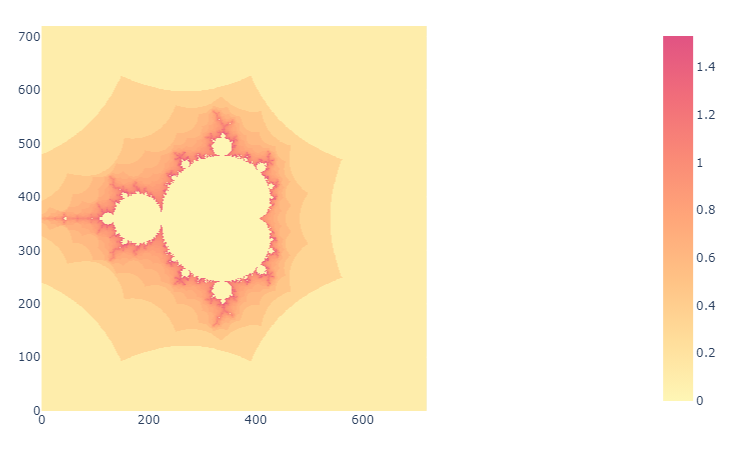
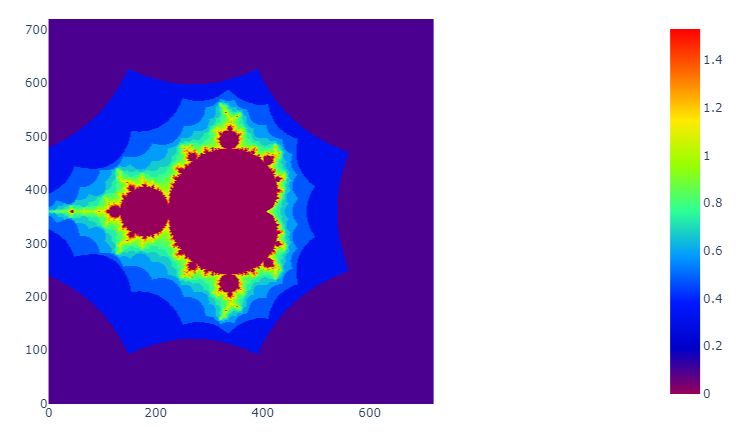
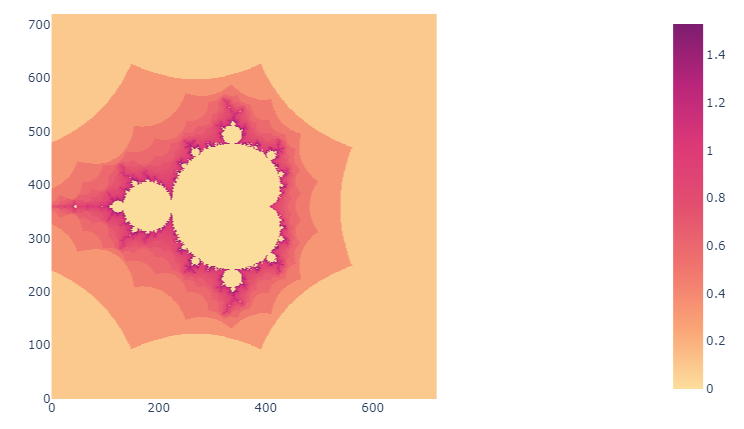
Réalisations
Ci-dessous, quelques exemples de l'ensemble de Mandelbrot avec différentes palettes de couleurs.