Fractales de Newton et sensibilité aux conditions initiales
Ce projet a été réalisé en Python sur PyScripter
Définition
Les fractales de Newton sont une représentation graphique des racines associées à chaque point complexe z d'un plan.
La fractale de Newton est définie dans le plan complexe et caractérisée par l'application de la méthode de Newton à un polynôme complexe.
Construction
On utilise la Méthode de Newton qui associe zn+1 à z - f(z)/f'(z).
Cette règle mène ensuite à une suite de points z1,z2,etc.. Si la suite converge vers une racine k du polynôme, alors z0 appartient à la région k.
Cette région est appelée "bassin d'attraction de la racine k".
Remarque
On remarque rapidement en regardant les fractales de Newton que des similarités se distinguent à toutes échelles.
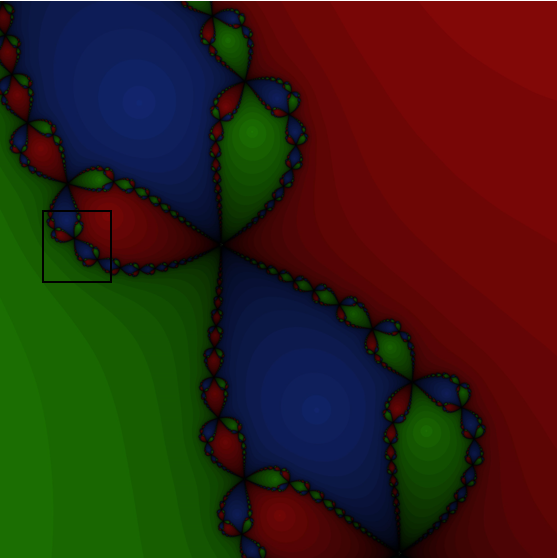
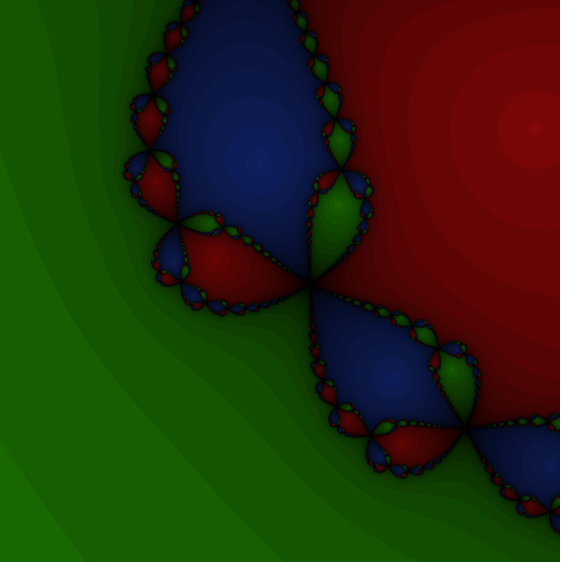Polynôme : z3-1
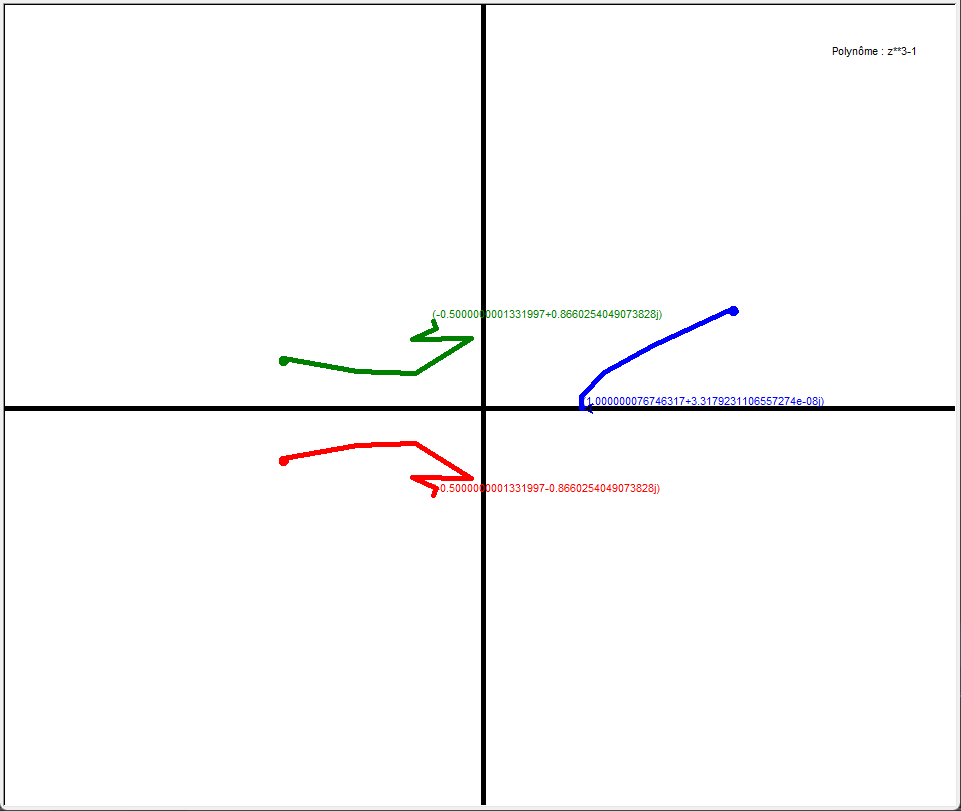
Cependant il existe aux frontières de ces bassins d’attraction des points pour lesquels on ne trouve aucune convergence.
Ces frontières très minces tendent à montrer une sensibilité très élevée aux conditions initiales : trois points très proches peuvent avoir une racine distincte.
Ici un décalage de +0.5i a été appliqué à chacun des points et ils ont tous une racine associée différente.
Programme
Ce programme a donc pour but de calculer puis dessiner une fractale à partir d'un polynôme complexe donné en paramètre.
Il nécessite les bibliothèques scipy et PIL :
from scipy.misc import derivative from PIL import Image
Initialisation
On crée une classe Fractale pour diminuer le nombre de paramètres de chaque fonction et rendre certaines variables globales.
On défini pour cette classe 6 variables :
- f : le polynôme complexe dont on veut la représentation
- N : le nombre maximal d’itérations que peut faire une suite avant d’être dite « non convergente »
- R : la liste des racines du polynôme
- L : la liste des z obtenu au terme de la suite de la méthode de Newton
- I : le nombre d’itérations nécessaire à chaque z pour atteindre une racine
- Palette : n’est autre que la palette de couleur utilisée pour dessiner les fractales
Ce qui donne ceci :
class Fractale:
def __init__(self,f,N=50):
self.f = f #Polynôme
self.N = N #Nombre maximal d'itération avant la "non-convergence"
self.R = [] #Liste des racines
self.L = [] #Liste des z finaux des points
self.I = [] #Liste du nombre d'iteration
self.palette = [(0,0,0),(255,255,255),(23, 49, 144),(174, 10, 10),(73, 53, 72),(38, 161, 0),(226, 219, 190),(134, 187, 216),(238, 66, 102),(184, 59, 21),(60, 187, 177),(64, 64, 64),(122, 122, 122),(192, 192, 192)]
Main
La fonction main est celle qui appellera toutes les autres pour assurer le bon fonctionnement du programme.
def main(self):
"""Programme principal"""
#Initialisation des variables
taille_img_x = int(input("Taille x de votre image (une taille impaire est préférable pour que le 0,0 soit centré)"))
taille_img_y = int(input("Taille y de votre image"))
im = Image.new('RGB', (taille_img_x, taille_img_y), (255, 255, 255)) #Crée une image blanche de la taille souhaitée
npix = 0
compteur = 0
pix_tot = taille_img_x*taille_img_y
#Set des coordonnées pour la création de z
for pix_x in range(taille_img_x):
for pix_y in range(taille_img_y):
coord = Fractale.coordonees(pix_x,pix_y,taille_img_x,taille_img_y)
x = coord[0]
y = coord[1]
z = complex(x,y)
#Recuperation des resultats de calcul_racine()
z_f = Fractale.calcul_racine(self,z) #Theoriquement proche d'une racine
#Definition de la racine
Fractale.set_racine(self,z_f)
compteur +=1
print((compteur/pix_tot*100)/2)
#Creation de l'image
for i in range(taille_img_x):
for j in range(taille_img_y):
im.putpixel((i,j), Fractale.set_color_pix(self,npix))
npix += 1
print(50+(npix/pix_tot*100)/2)
im.save("Images\\Finale_pres\\z^5-1.jpg","JPEG")
print("Votre image est prête")
Variables
Pour que le programme s'exécute correctement il faut commencer par initialiser quelques variables:
- La taille de l'image (en x et en y) - im : Une toile blanche de la taille souhaitée sur laquelle "dessiner" notre fractale - npix : ou numéro pixel qui servira plus tard pour le dessin - compteur et pix_tot servent à l'affichage en pourcentage de la progression du programme
Coordonnées
Pour avoir le résultat souhaité on travaille avec des z de petite taille (généralement entre 2+2i et -2-2i).
Pour ça il nous faut transformer les coordonnées pixels en coordonnées réelles. En effet les coordonnées d'une image et d'un plan ne sont pas traitées de la même façon :
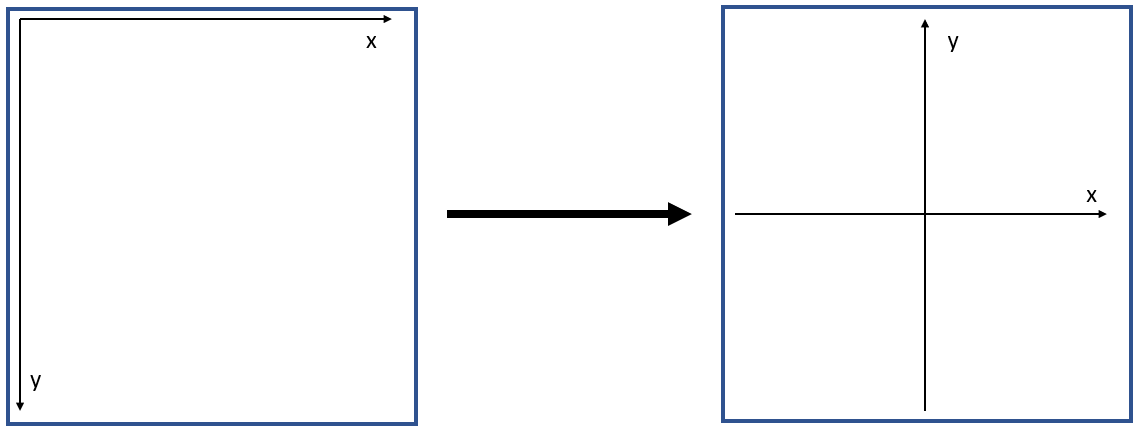
En résolvant un petit système :
def coordonees(pix_x,pix_y,taille_x,taille_y):
"""Transforme les coordonnées pixel en coordonnées réelles."""
x_hi = 2
x_lo = -2
y_hi = -2
y_lo = 2
x = (((x_hi-x_lo)/taille_x)*pix_x) + x_lo
y = (((y_hi-y_lo)/taille_y)*pix_y) + y_lo
return (x,y)
on obtient une équation et nous voilà avec des coordonnées utilisables pour nos calculs. On crée donc notre z complexe à partir du x et du y déduit de ce calcul.
Les paramètres x_hi / x_lo / y_hi / y_lo servent a définir la taille du plan complexe.
Calculs
Ce programme utilise la méthode de Newton, c'est un programme plutôt lent qui possède une complexité quadratique.
Avec le z calculé précédemment dans la fonction coord, on peut utiliser la méthode de Newton afin de trouver vers quelle racine il converge.
Pour cela on à besoin du module scipy et de sa fonction dérivative qui renvoi le résultat de la dérivée de notre fonction.
On défini donc Zn+1 comme étant z – f(z)/f’(z).
Compteur est le nombre d’itérations effectuées jusqu’à ce que z trouve une racine.
On stop donc la boucle de calcul si le nombre d’itérations dépasse N (un nombre arbitraire défini dans le init) ou si Zn+1 – Z est inférieur a 1*10-6 (la suite n’évolue plus).Théoriquement lorsque la suite se stabilise c’est que l’on se trouve proche d’une racine.
Une fois sorti de la boucle on ajoute à la variable globale I le nombre d’itérations effectuées pour ce z et on renvoi le z final obtenu.
def calcul(self,z):
"""Compte le nombre d'itérations nécessaire pour trouver une racine et s'arrête après N itérations."""
Zn_plus_1 = z - (self.f(z) / derivative(self.f,z,1e-12))
compteur = 0
while compteur < self.N and abs(Zn_plus_1 - z) >= 1e-6:
z = Zn_plus_1
Zn_plus_1 = z - (self.f(z) / derivative(self.f,z,1e-12))
compteur += 1
self.I.append(compteur)
return z
Différentes méthodes
Cependant, il existe d’autres méthodes ayant des résultats similaires avec des complexités moindre ou non.
On peut notamment citer la méthode de la sécante avec une complexité linéaire de 1.618 qui approxime la dérivée au lieu de la calculer mais qui a donc un résultat moins précis.
Pour utiliser ces autres méthodes il suffit de remplacer l'affectation de zn+1 par celle de la méthode souhaitée.
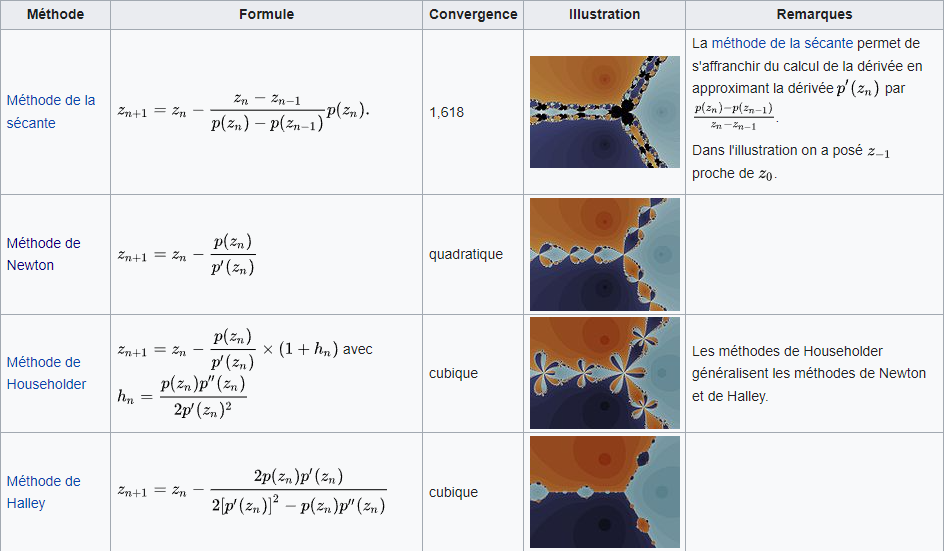
Source : Wikipédia/Fractales de Newton
Les racines
Comme vous l'avez certainement remarquer ce programme ne demande pas à l'utilisateur de renseigner les racines du polynôme.
Cependant pour que le programme fonctionne il faut avoir accès aux racines.
Pour cela il existe les variables globales R et L. Pour rappel L sert à enregistrer les zn obtenus en fin de process de la fonction calcul() et R est la liste des racines.
Or il faut remplir cette liste !
C'est la fonction set_racine() qui s'en occupe.
def set_racine(self,z):
"""Modifie le tableaux des racines R et celui des z finaux L."""
if self.R == []:
self.R.append(z)
self.L.append(z)
elif len(self.R) == 1:
if abs(self.R[0] - z) < 0.1:
self.L.append(z)
else:
self.R.append(z)
self.L.append(z)
else:
mini = abs(self.R[0] - z)
for i in range(len(self.R)):
if abs(self.R[i] - z) < mini:
mini = abs(self.R[i] - z)
if mini < 0.1:
self.L.append(z)
else:
self.R.append(z)
self.L.append(z)
Si R est vide on entre la valeur de notre zn actuel comme première racine et on ajoute zn à la liste L.
S’il n’y a qu’une seule racine on la compare à zn, s’ils sont trop éloignés alors on crée une deuxième racine (en ajoutant zn à R) puis on ajoute zn à L. Sinon on ajoute juste zn à la liste L sans ajouter de racine.
Enfin s’il y en a plus on compare une à une toutes les racines avec zn et on sélectionne la plus proche avant d’effectuer la même chose que pour le cas à une seul racine.
Dessin
Nous avons désormais toutes les clés pour la réalisation de la fractale.
Après avoir parcouru une première fois tout notre plan pour recueillir les informations nécessaires il faut à présent recommencer pour changer la couleur de chacun des pixels de notre image.
Pour cela j’ai utilisé la bibliothèque Image de PIL qui permet de modifier une image à sa guise.
Ainsi on peut sélectionner la couleur à associer au pixel en fonction de deux choses :
- Son nombre d’itération - La racine atteinte
Choix de la couleur
Pour savoir à quelles résultats se référer pour le pixel qui est traité on utilise la variable npix (initialisée au début de main()). Elle est ici sous la forme d'un compteur pour minimiser les calculs à effectuer :
for i in range(taille_img_x):
for j in range(taille_img_y):
im.putpixel((i,j), Fractale.set_color_pix(self,npix))
npix += 1
mais peut aussi être définie comme ceci :
for i in range(taille_img_x):
for j in range(taille_img_y):
npix = i*taille_img_y + j #somme des lignes parcourues et des pixels de la ligne en cours
im.putpixel((i,j), Fractale.set_color_pix(self,npix))
Le dessin fait appel à la fonction set_color_pix() :
def set_color_pix(self,npix):
"""Sélectionne la couleur en fonction de la racine atteinte."""
color = (0,0,0)
if self.I[npix] == self.N:
color = self.palette[0]
elif self.I[npix] == 0:
color = self.palette[1]
else:
#Definition de la couleur a choisir
index = 0
mini = abs(self.R[0] - self.L[npix])
for i in range(len(self.R)):
if abs(self.R[i] - self.L[npix]) < mini:
mini = abs(self.R[i] - self.L[npix])
index = i
color = self.palette[index + 2]
t = (1-(self.I[npix]/self.N))**2
color = (int(color[0]*t),int(color[1]*t),int(color[2]*t))
return color
Il y a deux cas de base pour lesquels le choix est rapide :
- Si son nombre d’itération est égal à N alors on applique une couleur noire (palette[0]).
- Sinon si son nombre d’itération est 0 alors c’est une racine et on lui donne un couleur blanche (palette[1]).
Cependant si notre zn atteint bien une racine alors il faut savoir laquelle.
Pour cela on réutilise une boucle de minimum semblable à celle de set_racine():
On compare les racines avec zn et on regarde quelle racine est la plus proche de zn.
On récupère donc l'index de la racine associée dans R. Comme les deux premières couleurs de notre palette (noir et blanc) sont déjà utilisées on utilise index+2 comme index à utiliser pour notre palette.
De plus on crée une variable t qui sert "d'atténuateur" que l'on multiplie aux 3 composantes RGB de nos couleurs. Ainsi plus le nombre d'itérations (I) de zn sera grand plus t sera proche de zéro et plus la couleur sera terne et proche du noir.
Une fois la bonne couleur choisie il ne reste qu'à remplacer le pixel en utilisant la fonction putpixel de la bibliothèque PIL.
Et une fois notre image entièrement traitée on l'enregistre.
Exemples
Voici quelques exemples de fractales réalisées avec mon programme.
Polynôme : z5-1
Polynôme : z6+z3-1
D'autres fractales réalisables.
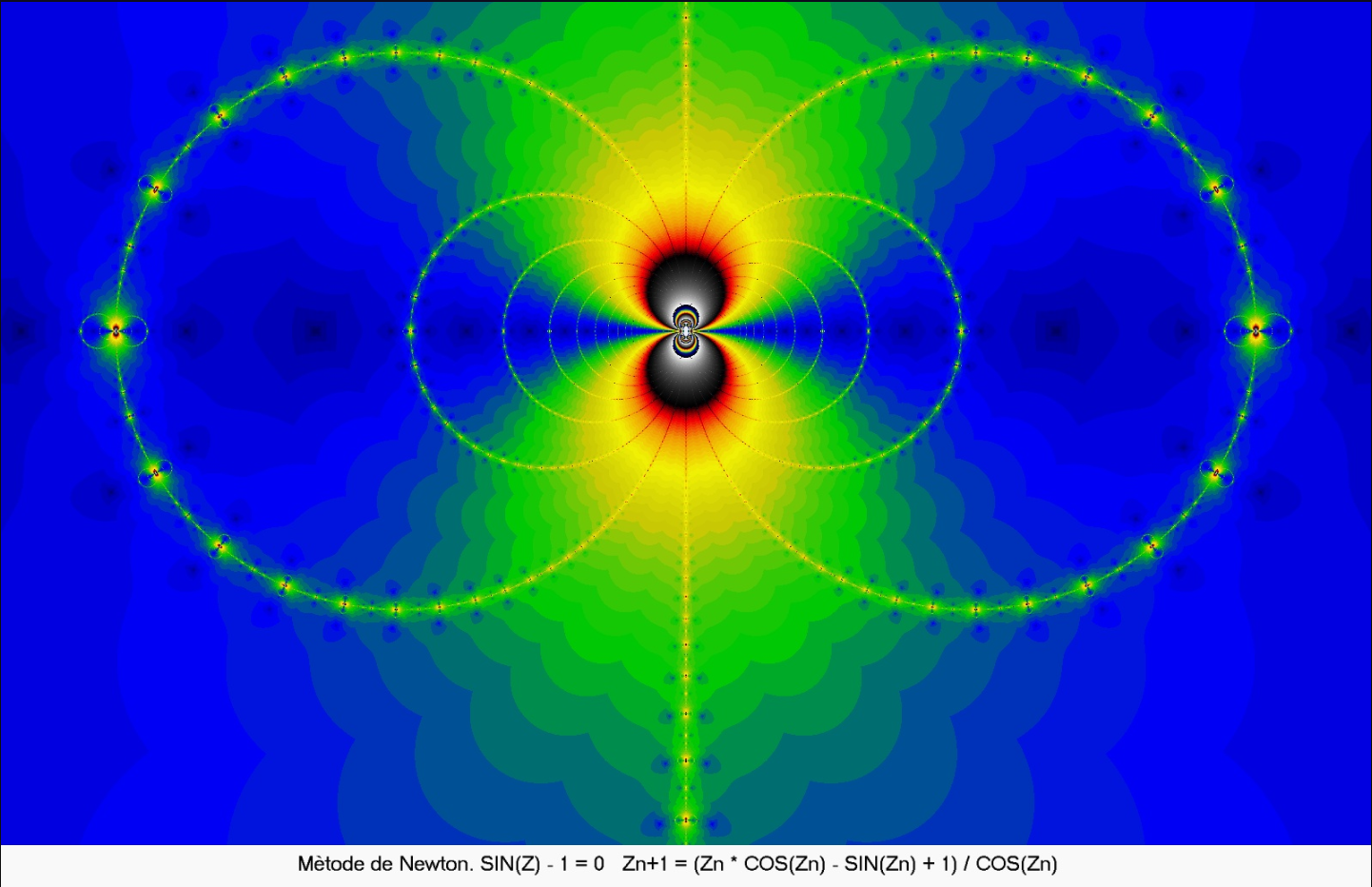Polynôme : sin(z)-1
Polynôme : cosh(z)-1