Génération et résolution de labyrinthes

• 2016-2017
• Tuteur : Xavier PROVENCAL
• Etudiant : Candice ROBERT

Les programmes sont réalisés en python et utilisent des librairies écrites par M Provencal

Approche mathématique des labyrinthes

Un labyrinthe est dit parfait si chaque cellule est reliée à toutes les autres, et ce d’une seule manière. Les labyrinthes imparfaits peuvent donc contenir des boucles, des îlots ou des cellules inaccessibles

Nous nous intéresserons aux labyrinthes parfaits. On peut modéliser leurs chemins par des graphes. Pour résumer, un graphe est un ensemble de sommets reliés par des arrêtes.

---

Génération de labyrinthes

La création d'un labyrinthe suit les étapes suivantes :

• Générer un graphe G représentant une grille de taille m*n
• Construire un arbre couvrant A de ce graphe
• Dessiner le labyrinthe en traçant un mur entre les sommets directement liés dans G et non dans A

Qu'est ce qu'un arbre couvrant ?

Un arbre est un graphe à la fois connexe et sans cycle. Un arbre couvrant d'un graphe est un arbre inclus dans ce graphe et qui connecte tous les sommets du graphe.

Algorithmes de construction de l'arbre couvrant

Parcours en largeur du graphe

On commence par explorer un nœud source, puis ses voisins, puis les voisins non explorés de ces voisins, etc

Voici la fonction qui réalise cet algorithme :

def parcoursLargeur(G):
    vu = set()
    L = deque() # insérer : L.append( ), retirer : L.popleft()
    A = Graph() # le graphe de notre labyrinthe
    A.add_vertices( G.vertices() )
    A.set_pos( G.get_pos() ) # juste pour l'affichage

    s = (0,0)
    vu.add(s)
    L.append(s)

    while len(L)>0:
        u = L.popleft()
        for v in G.neighbors(u):
            if v not in vu:
                A.add_edge(u, v)
                L.append(v)
                vu.add(v)
    return A

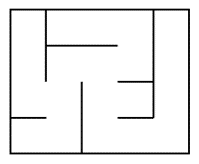
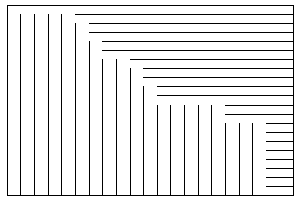
Et un résultat obtenu à partir de cette fonction :

Bien qu'il soit complètement régulier, il s'agit bien d'un labyrinthe parfait. Nous l'améliorerons plus tard.

Parcours en profondeur du graphe

Pour chaque sommet, on marque le sommet actuel, et on prend le premier voisin jusqu'à ce qu'un sommet n'ait plus de voisins (ou que tous les voisins soient marqués), et on revient alors au sommet père. C'est un algorithme récursif, c'est à dire qu'il fait appel à lui même.

def parcoursProfondeur(G) :
    vu = set()
    A = Graph()
    A.add_vertices( G.vertices() )
    A.set_pos( G.get_pos() ) 
    s = (0,0)
    parcoursProfondeurRec(G,s,A,vu)
    return A

def parcoursProfondeurRec(G,u,A,vu):
    vu.add(u)
    for v in G.neighbors(u):
        if v not in vu:
            A.add_edge(u,v)
            vu.add(v)
            parcoursProfondeurRec(G,v,A,vu) # Ici la fonction s'appelle elle-même !

Et un résultat obtenu :

Ajout d'aléatoire sur les deux dernières méthodes

Pour rendre les labyrinthes obtenus moins réguliers, nous avons ajouté un aspect aléatoire (dans l'ordre de sélection des voisins des sommets). Voici donc les nouvelles versions de parcoursLargeur ainsi que de parcoursProfondeur:

parcoursLargeur2

def parcoursLargeur2(G):
    """Ce programme choisi les voisins aléatoirement"""
    vu = set()
    L = deque() # insérer : L.append( ), retirer : L.popleft()
    A = Graph()
    A.add_vertices( G.vertices() )
    A.set_pos( G.get_pos() ) # juste pour l'affichage

    s = (0,0)
    vu.add(s)
    L.append(s)

    while len(L)>0:
        u = L.popleft()
        voisins = G.neighbors(u)
        for x in range(0,len(G.neighbors(u))):
            v = random.choice(voisins)
            if v not in vu:
                A.add_edge(u, v)
                L.append(v)
                vu.add(v)
            voisins.remove(v)
    return A

Le labyrinthe obtenu :

parcoursProfondeur2

def parcoursProfondeur2(G) :
    """Ce programme choisi les voisins aléatoirement"""
    vu = set()
    A = Graph()
    A.add_vertices( G.vertices() )
    A.set_pos( G.get_pos() ) 
    s = (0,0)
    parcoursProfondeurRec2(G,s,A,vu)
    return A

def parcoursProfondeurRec2(G,u,A,vu):
    vu.add(u)
    voisins = G.neighbors(u)
    for x in range (0,len(G.neighbors(u))):
            v = random.choice(voisins)
            if v not in vu:
                A.add_edge(u,v)
                vu.add(v)
                parcoursProfondeurRec2(G,v,A,vu)
            voisins.remove(v)

Le labyrinthe obtenu :

Nous avons donc pu voir que ces deux méthodes, bien qu'elles permettent effectivement de construire des labyrinthes, ont leurs limites. Le dernier résultat obtenu avec parcoursProfondeur2 se rapproche de ce qu'on souhaiterait obtenir, mais nous allons voir d'autres méthodes de générations de labyrinthe, afin de déterminer laquelle est la plus efficace.

Arbre couvrant minimum

On attribue (idéalement de manière aléatoire), des poids à chacune des arrêtes du graphe de départ. L'arbre couvrant minimum est l'arbre couvrant dont la somme des poids est minimale. Cela fonctionne également avec l'arbre couvrant maximal. L'aspect aléatoire donne un avantage sur les autres méthodes, puisque cela permet de construire un labyrinthe beaucoup plus équilibré.

Algorithme de Prim

On part d’un sommet du graphe. À chaque répétition, on ajoute à l'arbre le sommet libre accessible de poids minimal. On s'arrête quand l'arbre est recouvrant.

Cette première fonction attribue un poids (coefficient) à chacune des arêtes du graphe d'origine :

def attribuerPoids(G):
    """Attribue aléatoirement des poids aux arêtes du graphe G"""
    poids = {}
    for (u,v) in G.edges():
        x = random.uniform(0,1)
        poids[(u,v)]= x
        poids[(v,u)]= x
    return poids

La fonction principale :

def algoPrim(G) :
    attribuerPoids(G)
    A = Graph()
    A.add_vertices( G.vertices() )
    A.set_pos( G.get_pos() ) 
    vu = set()
    pere = {}
    nonVu = {}
    poidsAretes = attribuerPoids(G)
    for u in G.vertices() :
        nonVu[u]= float('inf') # à chaque sommet on associe un poids infini
        pere[u] = u # chaque sommet est son propre père
    s = (0,0) # tous les sommets ont poids infini sauf s qui a 0
    nonVu[s] = 0
    while G.num_verts()> len(vu):
        u = min(nonVu, key=nonVu.get)
        A.add_edge(u,pere[u])
        vu.add(u)
        for v in G.neighbors(u):
            if v not in vu:
                if poidsAretes[(u,v)] < nonVu[v] :
                    pere[v] = u # nouveau père pour v
                    nonVu[v] = poidsAretes[(u,v)]
        nonVu.pop(u)
    return A

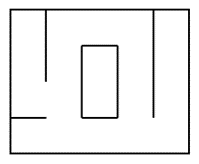
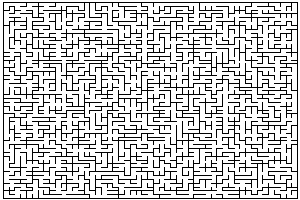
Le labyrinthe que génère cette fonction basée sur l'algorithme de Prim est le plus satisfaisant, puisque l'attribution aléatoire des coefficients est très efficace :

---

Sortie d'un labyrinthe

Il est assez connu qu'en longeant les murs d'un labyrinthes, on parvient à en sortir. Il faut pour cela que ce labyrinthe soit parfait. On peut parcourir le labyrinthe avec l'algorithme de parcours en profondeur vu précédemment. Cela revient à avancer tant qu'on le peut, et à retourner en arrière lorsqu'on est dans une impasse. Cette méthode n'est pas la plus courte. Le chemin le plus court peut être déterminé avec une file de priorité, par exemple avec l'algorithme de parcours en largeur.

Sortir d'un labyrinthe à l'aide du parcours en profondeur

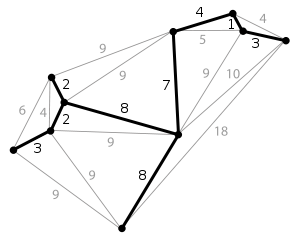
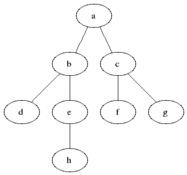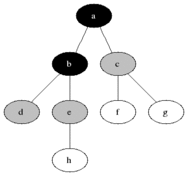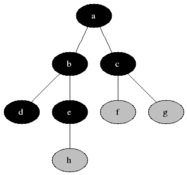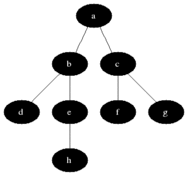
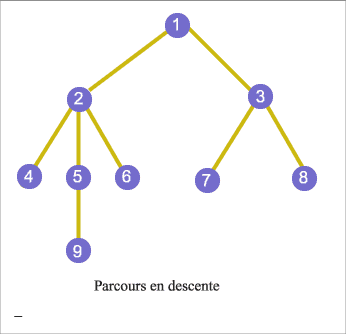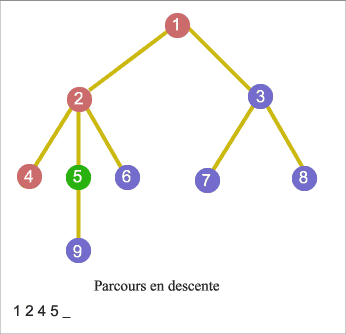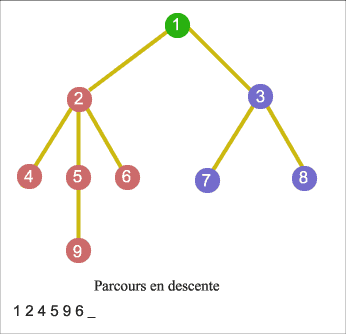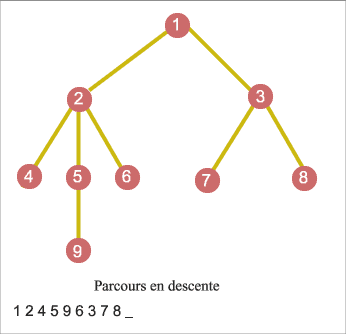
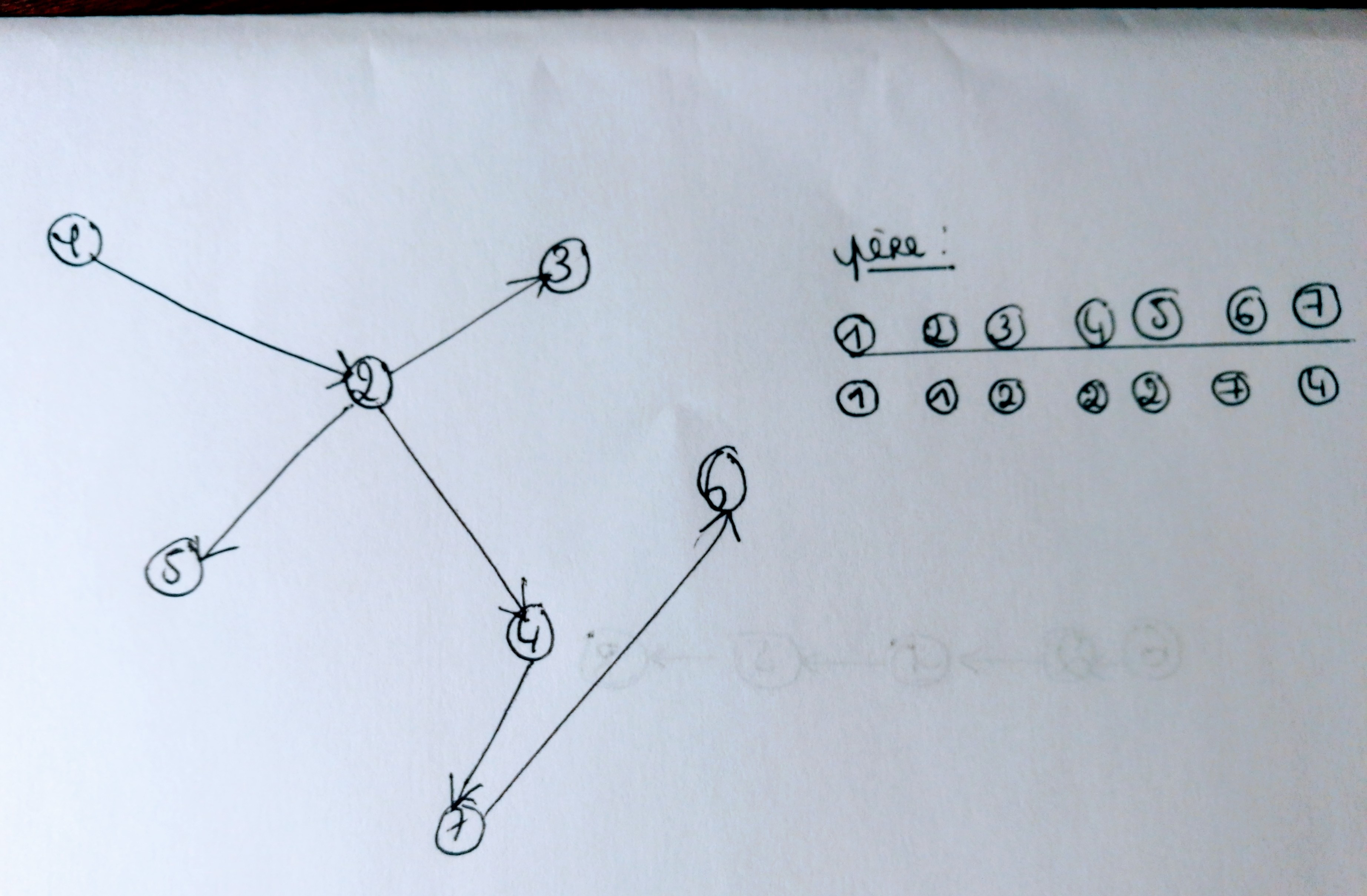
Voici un exemple pour expliquer la méthode :

Dans un premier temps, on oriente les arêtes. Un sommet ne peut avoir qu'un seul père. Le tableau joint au graphe donne pour chaque sommet son père (1 est son propre père). Ce sommet 1 correspond à l'entrée du labyrinthe, et 7 à sa sortie. Nous cherchons donc à déterminer le chemin menant de 1 à 7. Pour cela, on regarde dans le tableau le père de 7; il s'agit de 4. Le père de 4 est 2, et celui de 2 est 1. La solution du labyrinthe est donc : 1 > 2 > 4 > 7.

Si l'on traduit cela pour un algorithme, on a :

On initialise une variable s correspondant à la sortie du labyrinthe
On initialise une variable e correspondant à l'entrée
On initialise un dictionnaire pere qui associe à chaque sommet son père
Tant que s est différent de e on fait :
   s = pere[s]
   print(s)

---

Sources

• [1]
• [2]
• [3]
• [4]
• [5]