Génération et résolution de labyrinthes II
L'objectif de ce projet est de générer des labyrinthes aussi grands et complexes que possible. Nous allons voir comment toujours avoir un chemin entre l'entrée et la sortie, et comment trouver la sortie une fois notre labyrinthe généré.
Représentation
Propriétés
Tout d'abord, de manière assez informelle, un labyrinthe est une grille de cellules reliées, ou non, entre elles.
Deux cellules sont reliées entre elles par une porte, ou séparées par un mur.
Tout labyrinthe a une entrée et une sortie, et quelle que soit l'entrée ou la sortie, le chemin entre ces deux cellules est unique. Nous verrons cependant que ce dernier point peut varier, et introduire de nouvelles formes de labyrinthe.
Modélisation en graphe
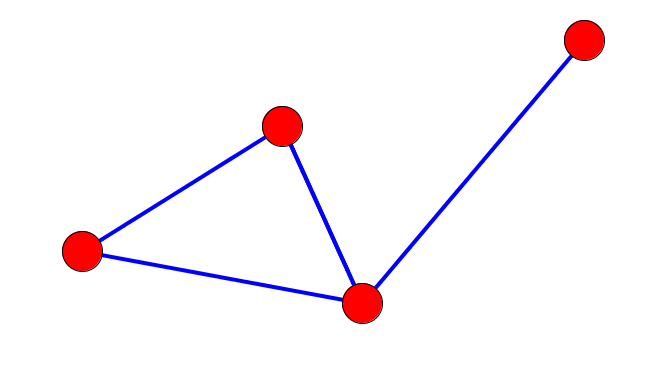
En théorie des graphes, un graphe est un ensemble de points (ou nœuds ou sommets) reliés ensemble par des lignes (ou liens ou arêtes).
Un graphe peut être dit connexe (d'un seul tenant) ou non connexe (en plusieurs morceaux).
Un graphe peut aussi être cyclique s'il existe au moins un chemin formant une boucle ou acyclique.
Enfin, un graphe peut être orienté (si les arêtes sont à sens unique) ou non orienté.
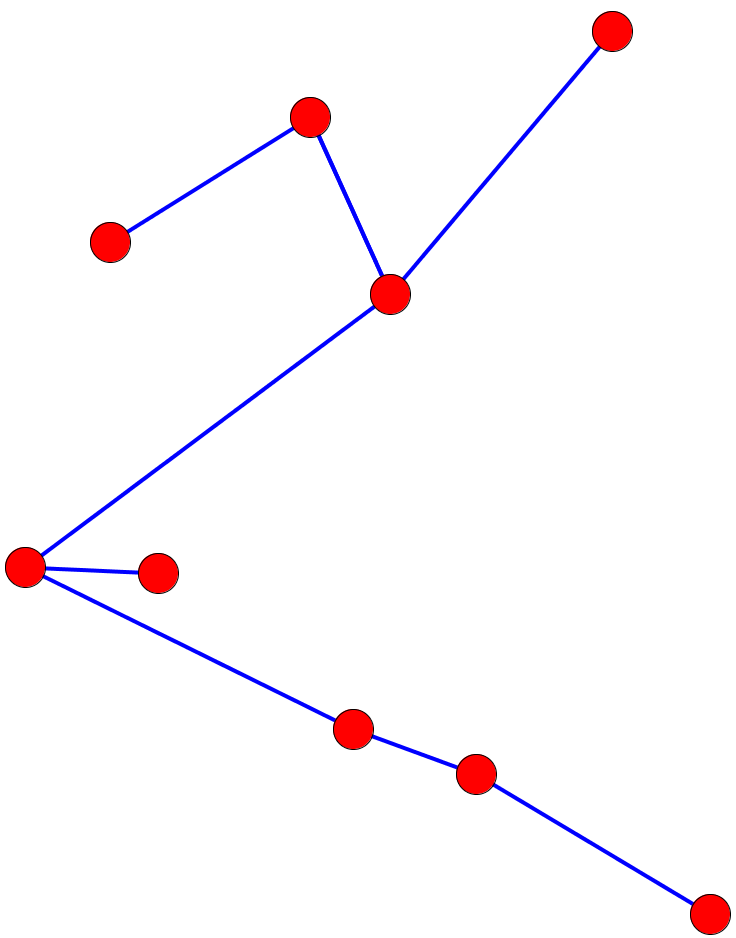
Un arbre est un graphe connexe, acyclique et non orienté.
Chaque feuille n'est connectée qu'à un seul autre nœud, et chaque sommet interne relie au moins deux nœuds.
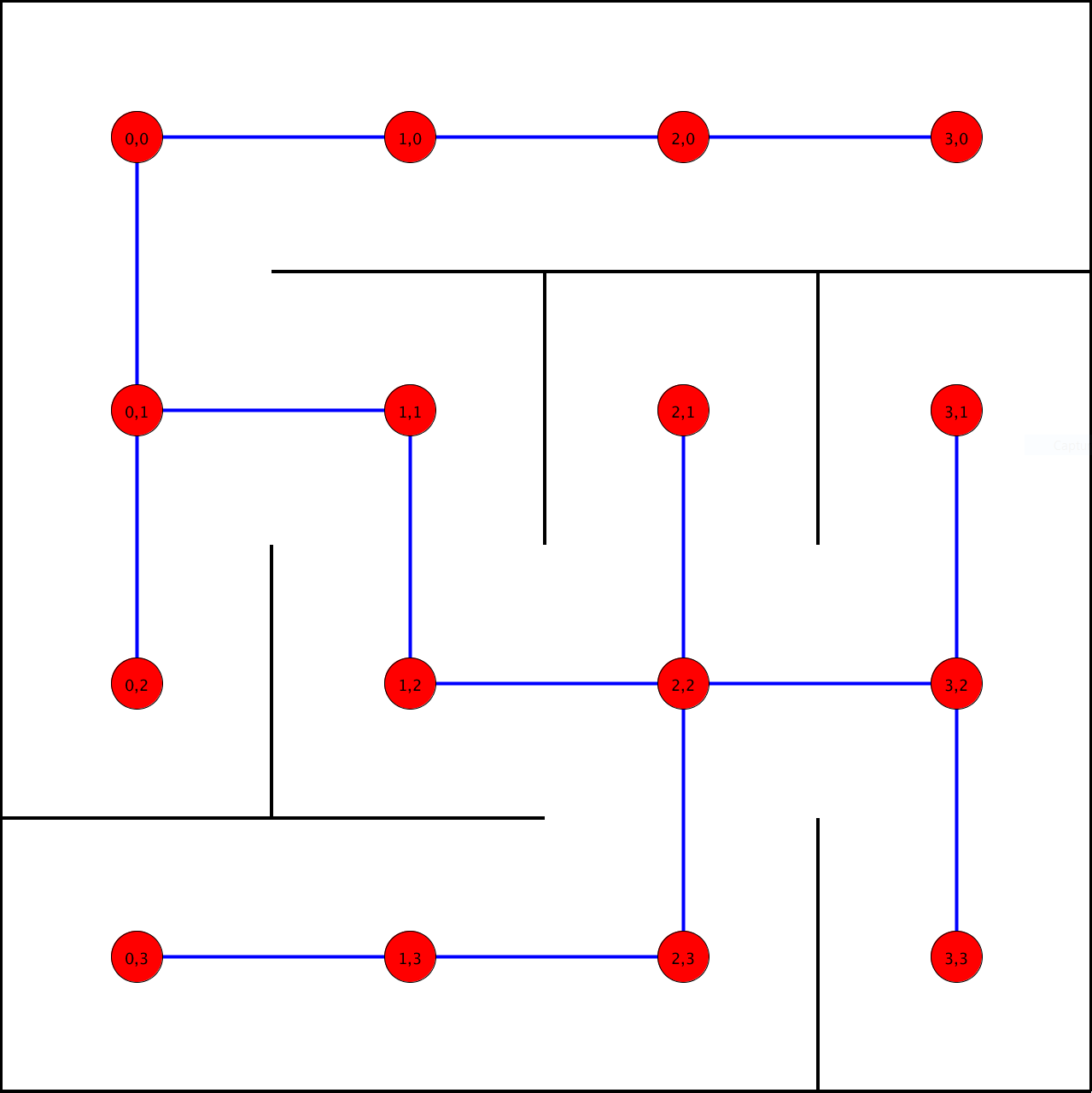
En plaçant un sommet sur chaque cellule de notre labyrinthe, et en reliant deux sommets par une arête si leurs cellules sont séparées par une porte, il devient possible de dessiner un arbre à partir de n'importe quel labyrinthe.
Sur notre graphe, un arête est donc un passage dans notre labyrinthe.
Génération
Un labyrinthe rectangulaire de largeur et de hauteur contient exactement portes.
Du point de vue du graphe, il y a donc arêtes.
Maintenant, comment répartir toutes ces portes de manière à ce que toutes les cellules soient accessibles et qu'il n'existe qu'un unique chemin entre l'entrée et la sortie ?
De nombreux algorithmes existent, dont le parcours en profondeur et l'algorithme de Kruskal. Chaque algorithme est différent et produit des labyrinthes visuellement différents.
Parcours en profondeur
L'algorithme du parcours en profondeur (ou "recursive backtracker" en anglais) commence sur une cellule aléatoire dans le labyrinthe.
Il suffit ensuite de se diriger dans une direction aléatoire et de casse le mur face à soi, tout en marquant la cellule précédente comme visitée.
Lorsque plus aucune direction n'est disponible, l'algorithme "remonte" à la position précédente : c'est le backtracking.
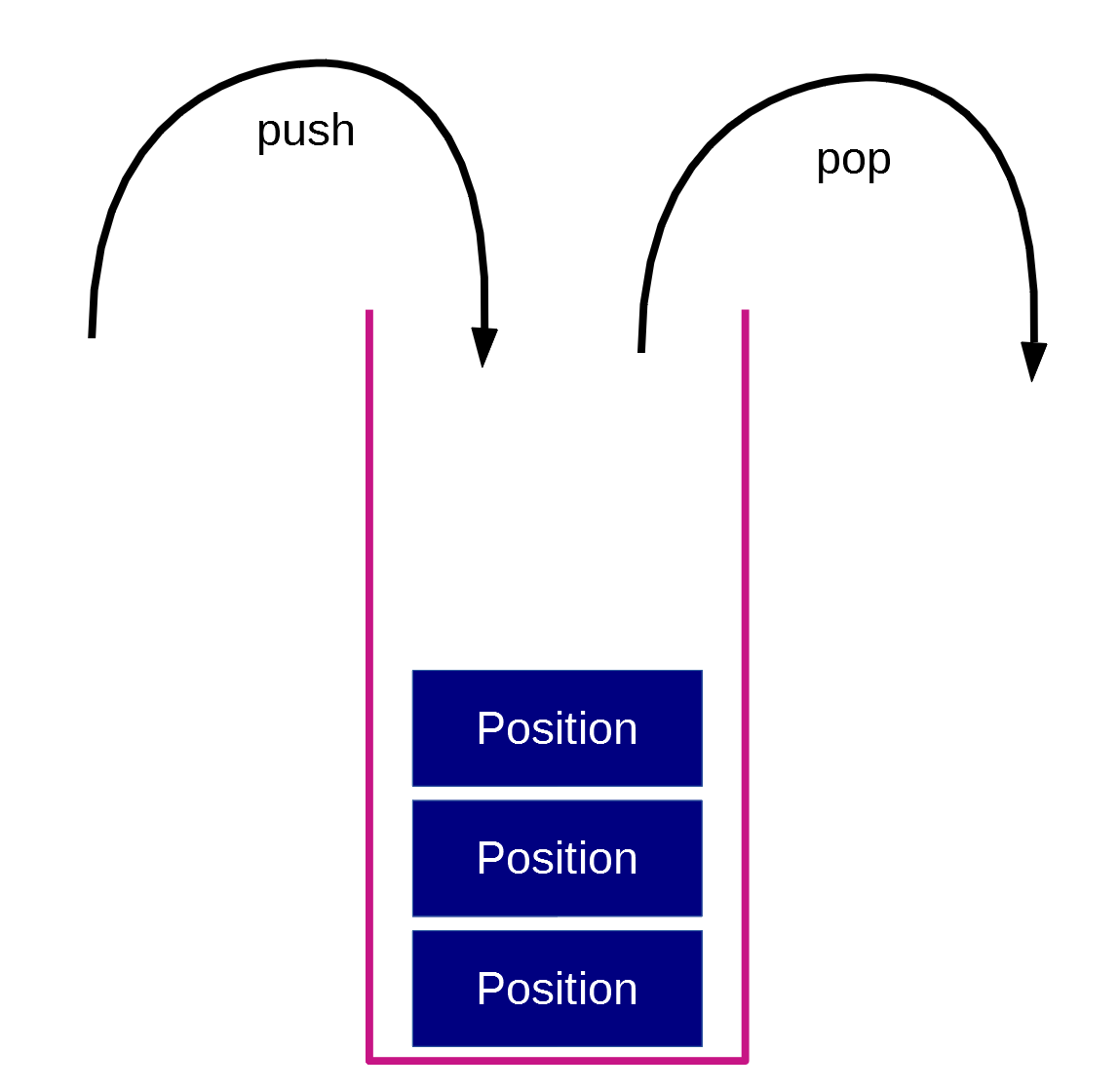
Une implémentation possible et pertinente pour sauvegarder l'historique des positions est la pile.
Une pile est une liste dans laquelle seul le dernier élément peut être récupéré.
Une pile est donc principalement composée de 2 méthodes :
push : elt -> ∅: ajoute un élément à la pilepop : ∅ -> elt: retourne le sommet de notre pile en retirant cet élément
Dans l'implémentation de la pile proposée, une erreur sera levée si la méthode méthode pop est appelée sur une pile vide.
Kruskal
Alors que le parcours en profondeur s'intéressait aux sommets, l'algorithme de Kruskal s'applique lui sur les arêtes.
Tout d'abord, chaque cellule se voit attributée un identifiant unique, dans un labyrinthe empli de murs.
Un mur aléatoire est ensuite choisi. Si les cellules séparées par ce mur ont des identifiants différents, le même identifiant leur sera associé, et il faudra alors abattre le mur.
Sinon, un autre mur sera choisi.
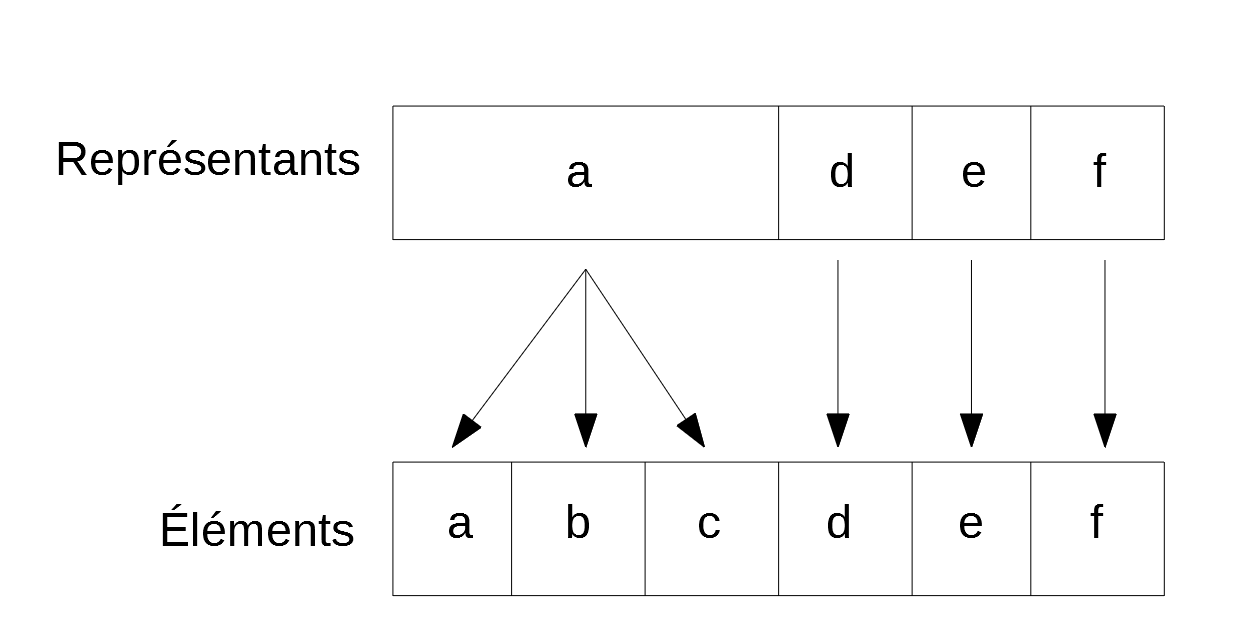
Pour mettre en œuvre cet algorithme, la structure la plus adaptée à utiliser est une structure de données appelée Union-Find, qui permet de mettre en relation des éléments partageant un même représentant (ou un même identifiant).
Il existe plusieurs variantes d'Union-Find, dont notamment la compression de chemin, qui permet de n'avoir qu'un ou deux éléments à parcourir pour obtenir le représentant d'un élément.
Union-Find fonctionne comme un arbre. 'a' a un représentant 'A', etc..., qui lui même a un représentant '', qui est son propre représentant.
Union-Find est composé de deux méthodes :
union : a, b -> ∅: associe à 'a' et 'b' le même représentant, par exemple 'A' le représentant de 'a'find : a -> r: tant que l'élément n'est pas son propre représentant,findest appliqué au représentant de l'élément.
On commence donc par find(a), puis find(A) (si 'A' est le représentant de 'a'), etc... La méthode de la compression de chemin permet d'éviter trop de récursivité en écrivant : représentant de 'a' = 'r'.
Pour les plus curieux, cette structure de données est décrite plus en détails dans un cours d'INFO602 qu'il est possible de retrouver ici.
Labyrinthes cycliques
Il est possible, en retirant un certain pourcentage de murs, de créer des labyrinthes cycliques à partir des labyrinthes acycliques générés auparavant.
Cependant, certains algorithmes de résolution n'adopteront pas le même comportement, voire ne fonctionneront même plus du tout.
Comparaison
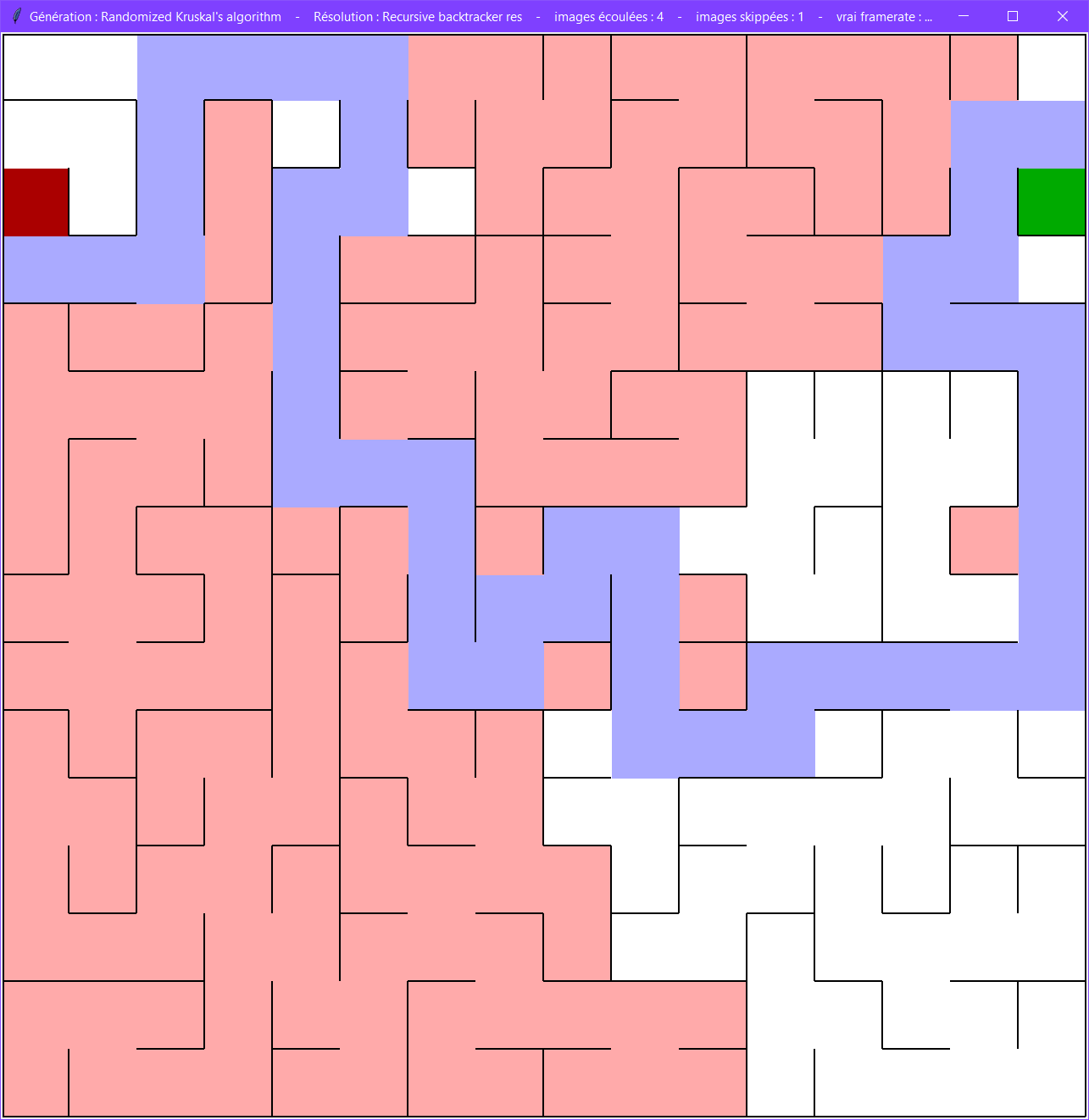
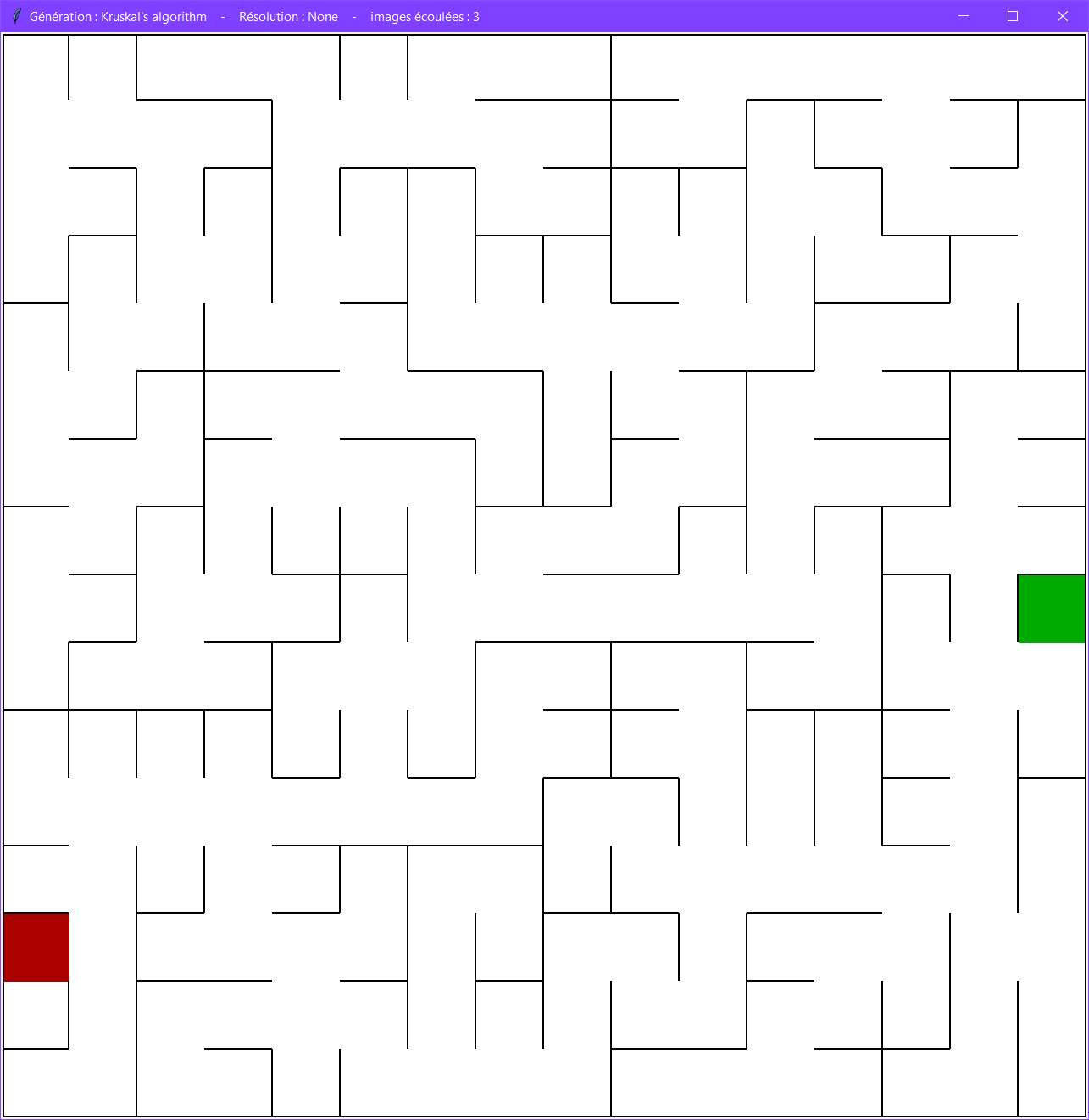
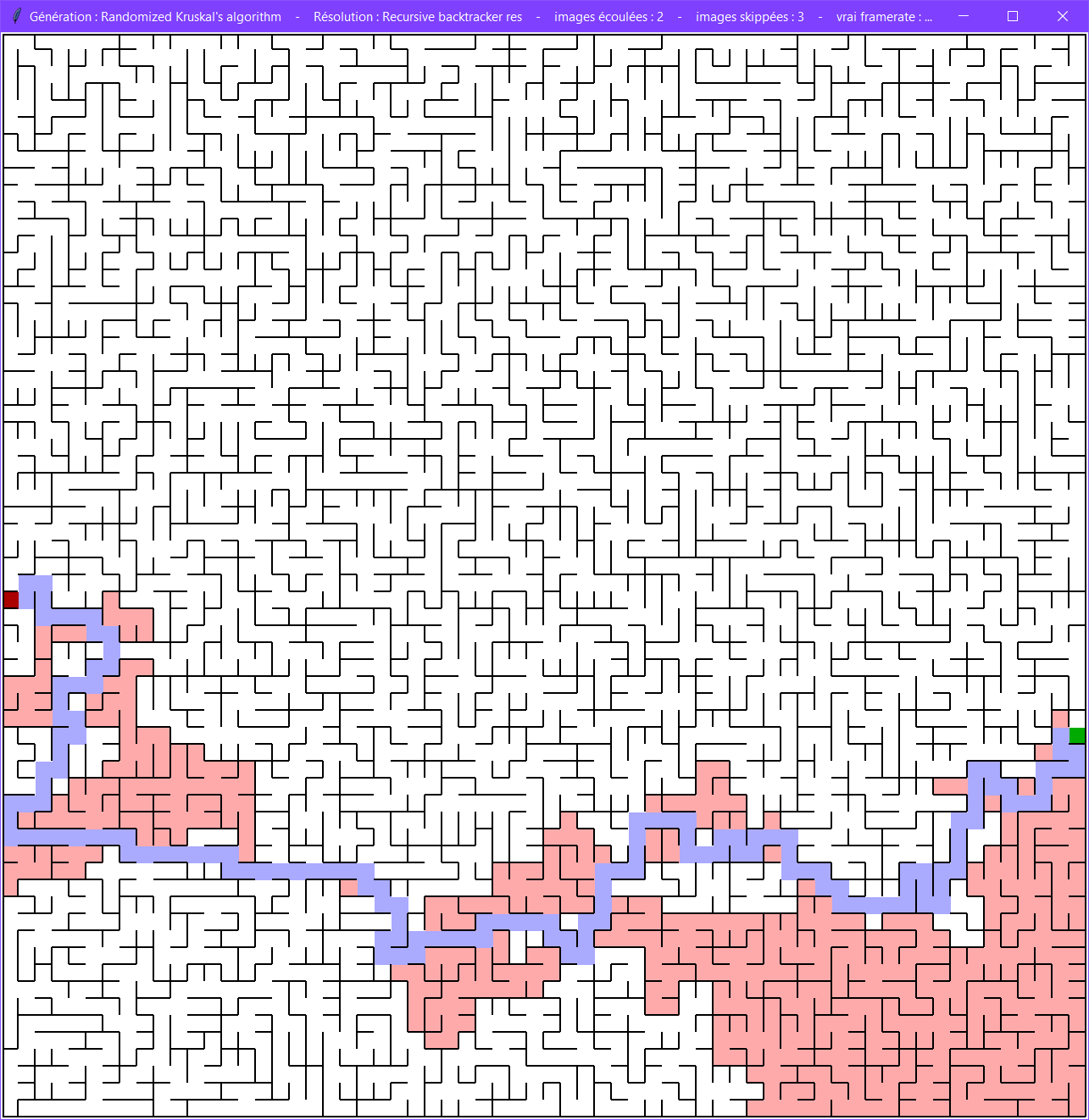
Il est possible de comparer un labyrinthe généré avec l'algorithme du parcours en profondeur à un labyrinthe généré avec l'algorithme de Kruskal.
Alors que ces deux algorithmes n'ont bien tous les deux qu'une unique solution, ils apparaissent néanmoins différents visuellement, et adoptent chacun leur propre structure.
Résolution
Il existe là encore de nombreux algorithmes de résolution de labyrinthes, plus ou moins efficaces, et surtout ne fonctionnant pas tous dans les mêmes conditions.
Parcours en profondeur
Cet algorithme est quasiment identique à celui du parcours en profondeur pour la génération.
Il est très efficace et trouvera une solution en minimisant le nombre de cases visitées.
Il s'adapte aux labyrinthes cycliques. En cas de boucle, il ne fera pas la boucle vu que l'intersection a déjà été visitées, il reviendra sur ses pas.
Il s'adapte aux labyrinthes sans solution. En effet, s'il n'y a pas de sortie, il va revenir à sa position de départ sans position précédente (pile vide) et en ayant parcouru toutes les cases.
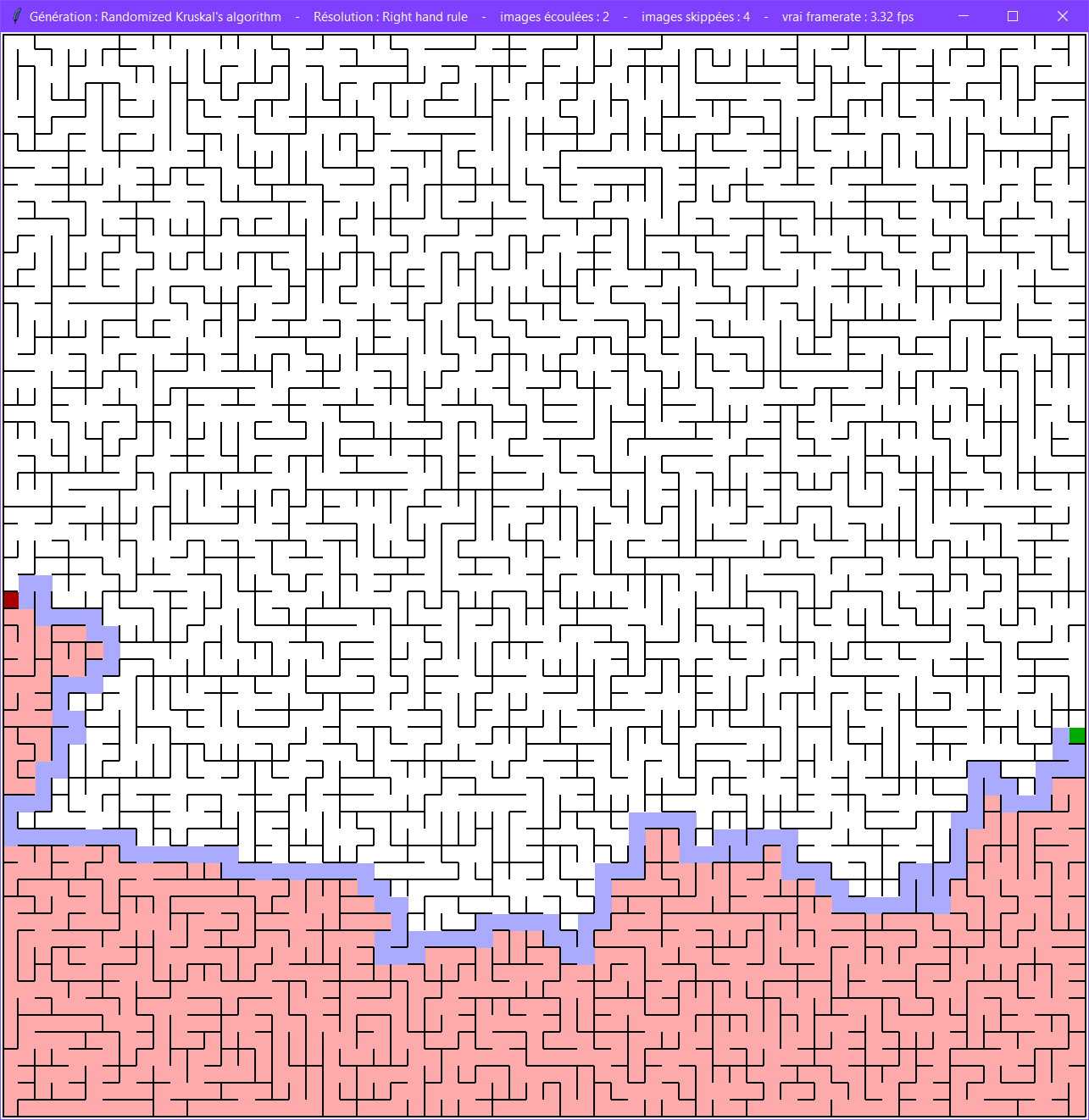
Mur droit
Cet algorithme va suivre de la main droite le mur de droite.
Il est relativement inefficace, et va visiter un grand nombre de cases.
Il s'adapte assez mal aux labyrinthes cycliques. En effet, si la sortie n'est pas dans la même boucle que l'entrée, il ne la trouvera jamais.
Il ne s'adapte pas aux labyrinthes sans solution, et fera le tour de la grille à l'infini.
On remarquera que des deux algorithmes, celui du mur droit explorera toutes les cellules situées en dessous du chemin optimal. Il sera donc plus efficace lorsque le chemin de solution est vers le bas de la grille.
Bilan personnel
Ce projet m'a permis de découvrir plusieurs structures de données qui, avec plusieurs années de recul, m'ont réellement été utiles.
J'ai aussi pu me familiariser avec Tkinter, avec la programmation orientée objets en Python (notamment héritage et méthodes statiques) et avec le multithreading, le projet ayant été pensé et codé en parallèle avant d'être entièrement refait plus "monolithique" une semaine avant l'oral.
J'ai aussi pu comprendre la complexité mathématique derrière un labyrinthe, et aborder certains aspects des graphes.
Pour résumer, ce projet a vraiment pris tout son sens en L3, où certains concepts m'ont enfin été expliqués et où j'ai enfin pu avoir le recul nécessaire pour saisir l'essence même de la problématique.
Code source
Le code source est disponible sur Github à cette adresse. N'hésitez pas à jeter un œil aux autres projets en cours 😉
Il suffit d'avoir installé Python 3 et Tkinter.
Sources et liens utiles
Génération
Résolution
Structures de données
Python