Géométrie discrète, Convexité des polyominos, Combinatoire des mots

Les images numérisées sont constituées de pixels, de petits carrés de couleurs. Les formes dans ces images ont alors une forme très particulière puisqu'il n'y a que quatres chemins possibles. Impossible d'aller en diagonale ou avec un angle particulier, les points n'ont que des coordonnées entières.
On peut alors retrouver les éléments de la géométrie Euclidienne classique dans Z² via un outil : les mots de Christoffel.
Cet outil permet de discrétiser des droites dans Z² afin de trouver la pente de celles-ci avec pour but d'appliquer les calculs de la géométrie Euclidienne.

---

Mot de Christoffel

On prend une droite de pente p/q et on veut dessiner une droite discrète de celle-ci en connectant des points de coordonnées entières dans Z².
On peut décrire cette droite comme "commençant" au point de coordonnée (0,0), passant par le point (p,q) et n'ayant que deux choix de mouvements :

• X pour se déplacer d'une unité à droite sur l'axe des abscisses.
• Y pour se déplacer d'une unité en haut sur l'axe des ordonnées.

Ainsi par exemple, on peut discrétiser la pente 2/3 en faisant les mouvements [x,x,x,y,y] ou [y,y,x,x,x].

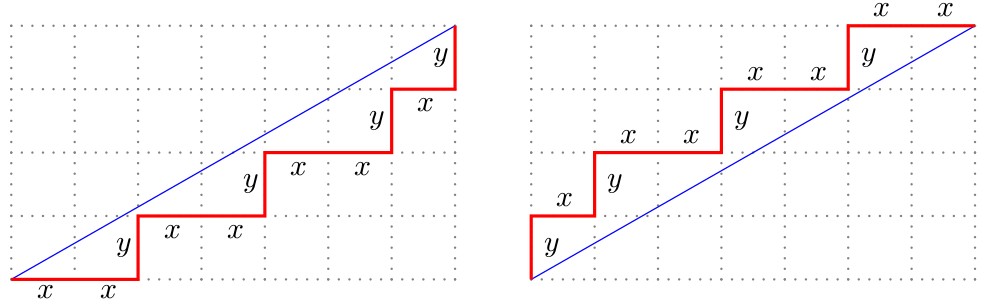
Un mot de Christoffel se base sur le même principe hormis qu'il va essayer de toujours être le plus proche possible de la ligne sans jamais la traverser.

Mot de Christoffel "bas" [x,x,y,x,x,y,x,x,y,x,y] et "haut" [y,x,y,x,x,y,x,x,y,x,x] de la droite de pente 4/7.

Note : Le mot de Christoffel "haut" est le mot de Christoffel "bas" lu à l'envers.
Note 2 : Si on retire la première et la dernière lettre d'un mot de Christoffel, on obtient un palindrome (lisible dans les deux sens) Note 3 : La première et la dernière lettre d'un mot de Christoffel sont forcément différentes.

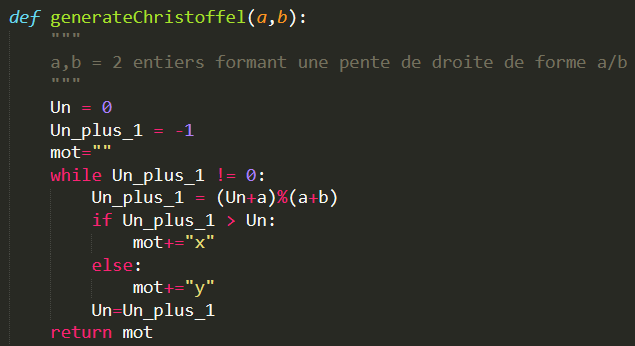
Algorithme de génération

Il est possible de générer facilement et très rapidement le mot de Christoffel d'une pente grâce à une méthode simple :

La suite U définie par : $U0=0|Un+1=(Un+a)[a+b]$ donnera une suite de chiffre qui se répète.
Si Un > Un+1, on ajoute un x au mot, sinon on ajoute un y au mot.

On applique cette méthode jusqu'à ce que Un+1 = 0 pour avoir le mot de Christoffel de la pente.

Exemple

Avec une pente de 5/7, on obtient :
0 5 10 3 8 1 6 11 4 9 2 7 0
Soit en appliquant la méthode : x x y x y x x y x y x y
On retrouve bien le mot de Christoffel de la pente 5/7 : [x,x,y,x,y,x,x,y,x,y,x,y]

Implémentation Python

Mot de contour

On peut définir un mot de contour comme un ensemble de mot de Christoffel étant orientés différemment les uns des autres.
Dans le cadre du module visi201, j'ai utilisé un algorithme pour le générer ayant le principe suivant :

• On considère en entrée une forme convexe noire sur un fond blanc.
• On crée une matrice avec la couleur de chaque pixel, c'est cette matrice qu'on traitera par la suite.
• On choisit deux points aléatoires jusqu'à ce qu'un d'eux soit noir et l'autre blanc.
• On applique le principe de dichotomie jusqu'à trouver un point étant le contour de la figure
• On parcourt la figure dans un sens arbitraire tout en restant "collé" à son contour
• Chaque mouvement est ajouté à une chaine de caractère sous forme de chiffre. (0 pour la droite, 1 pour le bas, ...)
• Dès qu'on retombe sur le point de départ de la figure, on a généré le mot de contour ayant 4 lettres : 0,1,2 et 3 pour chacun des mouvements.

Note : Un mot de contour n'est donc pas unique, il dépend de là où on commence le parcours de la figure.

Détection de droite discrète

La détection de la pente d'une droite discrète à partir d'un mot de Christoffel passe par un algorithme plus complexe que celui permettant de faire son opposé.

Algorithme

Cet algorithme se base sur le principe de "coincer" la discrétisation entre deux droites afin qu'il n'y ait qu'un point entier en ordonnée entre les deux droites pour chaque abscisse (toujours dans Z²).

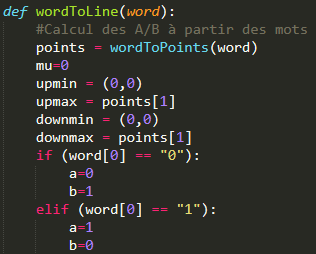
Initialisation

$\mu =0$
point d'appui haut minimal / upmin = (0,0)
point d'appui bas minimal / downmin = (0,0)
point d'appui haut maximal / upmax = 1er point du mot (donc (1,0) ou (0,1))
point d'appui bas maximal / downmax = 1er point du mot (donc (1,0) ou (0,1))
a=0/1 selon le premier point
b=0/1 selon le premier point

Implémentation python

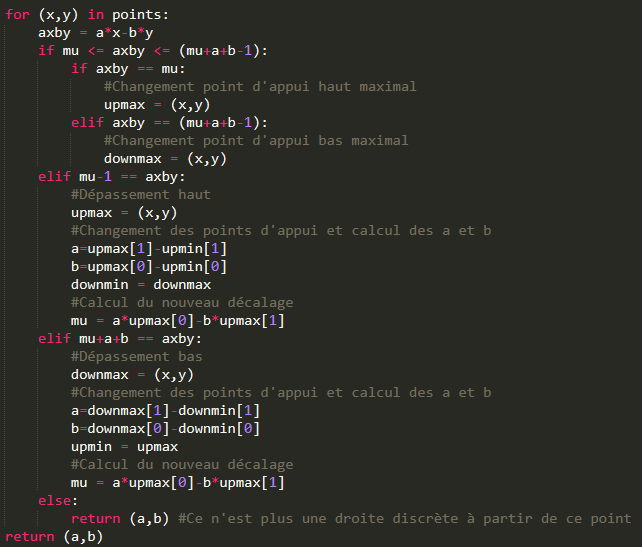
Itération : Implémentation python

Conclusion

Avec la pente des droites qu'on récupère via l'algorithme de détection des droites, on peut alors considérer une droite discrètiser comme une droite banale de R² et donc retrouver les formes de R² à partir des formes dans la géométrie de Z² et ainsi aisément retrouver tout les éléments de la géométrie Euclidienne classique. Le périmètre, la convexité et les points d'intersection sont alors calculable par exemple.

Les mots de Christoffel permettent donc un passage d'une géométrie de Z² à des éléments de la géométrie Euclidienne classique.

Sources et références

1. Lyndon + Christoffel = Convex Hull (bollu github)[1]
2. Géométrie discrète linéaire asymptotique et applications [2]