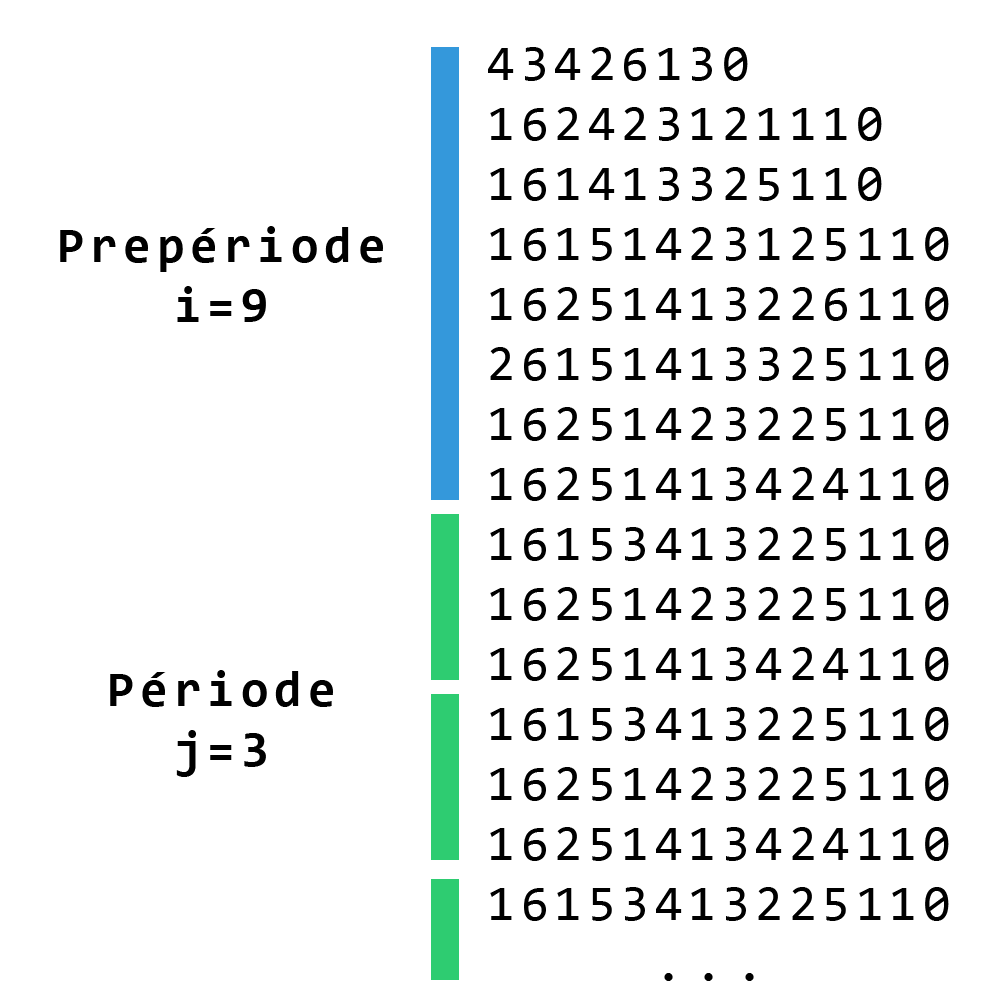La suite de Conway et la classification périodique des "éléments"

La suite de Conway, aussi appelée suite audioactive ou Look and Say sequence pour « Regarde et Dit » en anglais, est une suite mathématique créée par J. H. Conway en 1986.

Définition

Comme dit précédemment, la suite de Conway est une suite « audioactive ». Un terme se détermine en lisant le terme précédent.

Un terme est une chaîne de caractères constituée de chiffres.

Si l'on pose comme premier terme $C_{0}=333$ , on peut lire ce terme dans la vie courante comme « trois trois ».

Notre terme suivant sera donc $C_{1}=33$ . En appliquant cette même méthode, on trouvera les termes suivants :

$C_{2}=23$ ,

$C_{3}=1213$ ,

$C_{4}=11121113$ ,

$C_{5}=31123113$ ,

Et ainsi de suite.

On remarque que la méthode qui permet de passer du terme à son terme suivant est une méthode de compression appelée Run-length encoding (RLE)

Les fonctions qui permettent de calculer cette suite sont les suivantes :

def termeSuivant(terme):
    """Fonction qui retourne le terme suivant de la suite de Conway.
    Entrée: Chaîne de caractères ;
    Sortie: Chaîne de caractères ;"""

    nouveauTerme = ""
    c_actuel = terme[0]
    c_compte = 0

    for c in terme:

        if (c != c_actuel):
            nouveauTerme += str(c_compte) + c_actuel
            c_actuel = c
            c_compte = 1
        else:
            c_compte += 1

    nouveauTerme += str(c_compte) + c_actuel
        
    return nouveauTerme



def conway(n,premierTerme = "1",afficher = True):
    """Fonction qui affiche, puis retourne la suite de Conway jusqu'à un rang n.
    Entrée: n = Entier ; premietTerme (option) = Chaîne de caractère ; afficher (option) = Booléen.
    Sortie: Tableau de chaînes de caractère"""

    terme = premierTerme
    resultat = [""] * n
    
    for i in range(0,n):

        resultat[i] = terme

        if (afficher):
            print(terme)

        terme = termeSuivant(terme)

    return resultat

Exemple d'exécution :

>>> conway(5,premierTerme='42',afficher=False)
['42', '1412', '11141112', '31143112', '132114132112']

>>> termeSuivant('311212322')
'13211211121322'

Propriétés et théorèmes

Conway s'est demandé ce qu'il se passerait si l'on dérive n fois une chaîne de caractères d'entiers positifs.

Notion d'atome

Conway s'est rendu compte que peu importe la chaîne de départ choisi, on retrouve plusieurs fois certaines sous-chaînes.

Il en déduira le théorème de la séparation, qui décrit si une chaîne peut être découpée en deux sous-chaînes (la partie gauche et la partie droite) selon certains critères énoncés plus loin.

On appellera donc atome ou élément toute chaîne qui ne peut pas être coupée selon ce théorème.
On appellera composés les chaînes constituées de plusieurs atomes.

Propriétés

Voici les propriétés de certains théorèmes qu'il a trouvé.

Si le premier terme de la suite ne contient pas de chiffre 4 ou supérieur, alors les descendants de la suite n'auront pas de chiffre 4 ou supérieur.

Le théorème « chimique »

Les descendants de n'importe quel des 92 éléments de notre tableau périodique sont des combinaisons de ces éléments.
En dérivant assez de fois n'importe quel de ces éléments excepté l'hydrogène, on retrouvera l'ensemble des 92 éléments de notre tableau périodique.
En dérivant assez de fois n'importe quel chaîne de caractères autre que "" et "22", on retrouvera l'ensemble des 92 éléments de notre tableau périodique.

Le théorème « arithmétique »

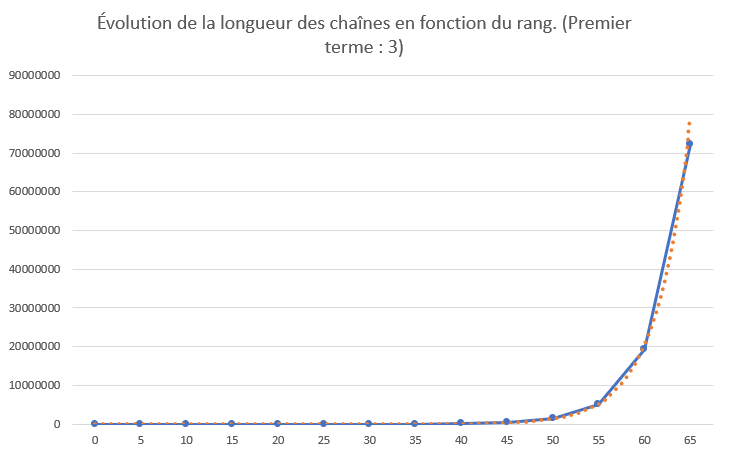
Excepté pour les premiers termes de la suite et pour les premiers termes "" et "22", la longueur des termes de la suite croit exponentiellement selon une constante :

\lambda =\lim _{n\rightarrow +\infty }{\frac {L_{n+1}}{L_{n}}}\simeq 1,30357726903

avec $L_{i}$ la longueur du i-ème terme de la suite.

L'abondance de ces éléments tendent vers des valeurs constantes, toutes positives.

Afin d'approximer et de vérifier expérimentalement la valeur de $\lambda$ , on peut calculer à l'aide de la fonction conway() vue précédemment un terme de rang n très grand et faire la division de sa longueur par la longueur du terme qui le précède.

Malheureusement, la fonction est gourmande en ressources et prend près de 10 minutes pour calculer le 65ème.

Il fallait donc soit changer le langage de programmation, soit changer l'algorithme.

En copiant la fonction conway() en langage C++, le temps de traitement n'a pas changé significativement.

J'ai fini par utiliser la fonction suivante, qui m'a permis de calculer 75 termes en quelques minutes.

import time
def conway(nbr=80):
    n = "1"
    for i in range(nbr):
        n=n.replace('111','ca').replace('222','cb').replace('11','ba').replace('22','bb').replace('33','bc').replace('1','aa').replace('2','ab').replace('3','ac').replace('a','1').replace('b','2').replace('c','3')
        yield n

Malgré ce gain de temps, il est difficile de stocker la suite. En effet, un fichier texte contenant les 70 premiers termes de la suite (avec comme premier terme "3") pèse plus d'un gigaoctet.

Au final, on peut trouver $\lambda =1,303600266$ avec $n=70$ et $C_{0}=1$ ou $\lambda =1,3035830259$ avec $n=65$ et $C_{0}=32$

Le théorème « cosmologique »

Toute chaîne de caractères décomposée assez de fois est une combinaison d'éléments du tableau périodique.

La conséquence de ceci est que chaque chaîne autre que "" et "22" a une longueur qui croit selon $\lambda$ , et l'abondance de chacun de ces atomes approche les valeurs décrite précédemment.

Le théorème de la « séparation »

Notation :

X signifie un chiffre non nul.

« $X]$ » désigne une chaîne qui se termine par X.

« $[X$ » désigne une chaîne qui se commence par X.

« $X^{i}$ » désigne une répétition de X, i fois. (e.g. $2^{4}\Leftrightarrow 2222$ )

Une chaîne GD ayant été décomposé au moins 2 fois peut se découper en deux chaînes G et D si l'une des conditions suivantes est respectée.

Pour $n\geq 4$ et $m\leq 3$ :

G (partie gauche)	D (partie droite)
$n]$	$[m$
$2]$	$[1^{1}X^{1}$ ou $[1^{3}$ ou $[3^{1}X^{\neq 3}$ ou $[n^{1}$
$\neq 2]$	$2^{2}1^{1}X^{1}$ ou $[2^{2}1^{3}$ ou $2^{2}3^{1}X^{\neq 3}$ ou $[2^{2}n^{(0ou1)}$

Tableau périodique

En suivant les théorèmes énoncés précédemment, on retrouve le tableau périodique avec l'abondance des atomes, leurs numéro et les chaînes correspondantes.

Voici les 20 premiers atomes des 92 éléments du tableau périodique :

Abondance	n	$E_{n}$	$E_{n}$ dans la dérivée de $E_{n+1}$
102.56285249	92	U	3
9883.5986392	91	Pa	13
7581.9047125	90	Th	1113
6926.9352045	89	Ac	3113
5313.7894999	88	Ra	132113
4076.3134078	87	Fr	1113122113
3127.0209328	86	Rn	311311222113
2398.7998311	85	At	Ho.1322113
1840.1669683	84	Po	1113222113
1411.6286100	83	Bi	3113322113
1082.8883285	82	Pb	Pm.123222113
830.70513293	81	Tl	111213322113
637.25039755	80	Hg	31121123222113
488.84742982	79	Au	132112211213322113
375.00456738	78	Pt	111312212221121123222113
287.67344775	77	Ir	3113112211322112211213322113
220.68001229	76	Os	1321132122211322212221121123222113
169.28801808	75	Re	111312211312113221133211322112211213322113
315.56655252	74	W	Ge.Ca.312211322212221121123222113
242.07736666	73	Ta	13112221133211322112211213322113

L'abondance d'un atome est en moyenne le nombre de fois qu'il apparait sur 1 million d'atomes.

On remarque que la décomposition de rhénium (Re) est combinaison du germanium (Ge), du calcium (Ca) et du tungstène (W).

La suite de Robinson

Définition

La suite de Robinson est une modification de la suite de Conway. En effet, on ne fait plus de compression RLE, mais on compte le nombre de fois qu'un chiffre apparait dans toute la chaîne.

En posant comme premier terme de la suite $R_{0}=2$ , on trouvera les termes suivants :

$R_{1}=12$

$R_{2}=1211$

$R_{3}=1231$

$R_{4}=131221$

$R_{5}=132231$

$R_{6}=232221$

$R_{7}=421311$

Et ainsi de suite.

Le programme permettant de calculer cette suite est le suivant :

def termeSuivantRobinson(terme):
    """Fonction qui retourne le terme suivant de la suite de Robinson.
    Entrée: Chaîne de caractères ;
    Sortie: Chaîne de caractères ;"""

    resultat = ""
    maximum = 0

    for c in terme:

        c = int(c)

        if (c > maximum):

            maximum = c

    for i in range(maximum, -1, -1):

        compte = 0
        
        for c in terme:

            if (int(c) == i):

                compte += 1
        if (compte != 0):
            resultat += str(compte) + str(i)

    return resultat
            
            
    
def robinson(n,premierTerme = "0",afficher = True):
    """Fonction qui affiche, puis retourne la suite de Robinson jusqu'à un rang n.
    Entrée: n = Entier ; premietTerme (option) = Chaîne de caractère ; afficher (option) = Booléen.
    Sortie: Tableau de chaînes de caractère"""

    terme = premierTerme
    resultat = [""] * n
    
    for i in range(0,n):

        resultat[i] = terme

        if (afficher):
            print(terme)

        terme = termeSuivantRobinson(terme)

    return resultat

Exemple d'exécution :

>>> robinson(6,premierTerme='21',afficher=False)
['21', '1211', '1231', '131221', '132231', '232221']

>>> termeSuivantRobinson('111352211321')
'15233261'

Propriétés

Exemple de boucle avec la prepériode et la période

En décomposant i fois un terme de la suite, la suite bouclera avec j descendants par boucle.

On appelle i la préperiode, et j la période de la suite.

On peut le vérifier expérimentalement avec cette fonction :

def trouverBoucle(premierTerme="0"):
    """Fonction qui trouve à quel rang la suite de Robinson boucle.
    Entrée : premierTerme (option): Chaîne de caractères ;
    Sortie : Tuple d'entiers. (prépreiode,periode)"""
    
    robinson = [premierTerme]
    dernierTerme = premierTerme
    
    i = 0   #Rang a partir duquel la suite boucle : préperiode
    j = 0   #Taille de la boucle : periode

    while (chaineDansListe(dernierTerme,robinson[:len(robinson) - 1]) == -1):   #Tant que le dernier terme n'est pas dans la suite
        
        robinson += [termeSuivantRobinson(dernierTerme)]

        dernierTerme = robinson[len(robinson) - 1]

        i += 1

    j = i - chaineDansListe(dernierTerme,robinson[:len(robinson) - 1])
    
    return (i,j + 1)

Approfondissements possibles

On pourrait utiliser les chiffres romains au lieu des chiffres arabes pour générer notre suite.

Source et documents annexes

Source

Conway, J. H. "The Weird and Wonderful Chemistry of Audioactive Decay." §5.11 dans Open Problems in Communication and Computation (Ed. T. M. Cover and B. Gopinath). New York: Springer-Verlag, pp. 173-188, 1987.

Annexes

La suite de Conway et la classification périodique des "éléments"

Sommaire

Définition

Propriétés et théorèmes

Le théorème « chimique »

Le théorème « arithmétique »

Le théorème « cosmologique »

Le théorème de la « séparation »

Tableau périodique

La suite de Robinson

Définition

Propriétés

Approfondissements possibles

Source et documents annexes

Menu de navigation

La suite de Conway et la classification périodique des "éléments"

Définition

Propriétés et théorèmes

Le théorème « chimique »

Le théorème « arithmétique »

Le théorème « cosmologique »

Le théorème de la « séparation »

Tableau périodique

La suite de Robinson

Définition

Propriétés

Approfondissements possibles

Source et documents annexes

Menu de navigation

Rechercher