Modélisation de réseaux sociaux, base de données orientées graphe

Qu'est-ce qu'un graphe ?

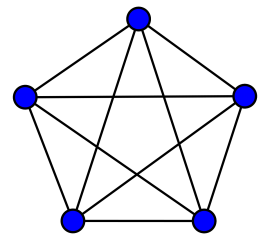
Un graphe est la donnée d’un ensemble de points qu’on appelle des sommets et d’un ensemble de ligne qu’on appelle des arêtes reliant certains sommets entre eux. On peut aussi noter qu’un graphe est dit complet lorsque deux sommets quelconques distincts sont toujours adjacents. Autrement dit, tous les sommets sont reliés deux à deux par une arête, comme sur la deuxième image par exemple.

graphe de réseau "petit monde"

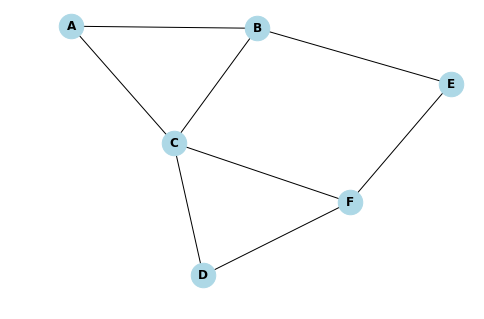
Pour ce projet, on cherche à modéliser un réseau social se présentant sous forme de graphe, un réseau social est un réseau "petit monde". Un réseau "petit monde" est un réseau dans lequel chaque individu peut être relié à n’importe quel autre individu par une courte chaîne de relations sociales. Le réseau « petit monde » est un modèle mathématique utilisé pour modéliser des réseaux réels, notamment des réseaux sociaux.

Ce concept reprend l’expérience de Stanley Milgram en 1967 avec son concept de « six degrés de séparation ». Les réseaux sociaux ont la propriété de petit monde qui est capturé par ce modèle : dans la majorité des cas, deux nœuds, c’est-à-dire deux personnes, peuvent être reliés par un très petit nombre d’amis intermédiaires.

Créations des graphes

Nous allons ensuite créer un graphe aléatoire à l'aide des algorithmes suivant:

Le premier algorithme permet de créer un graphe représentant l'invitation dans le réseau de nouveaux individus, le graphe sera donc représenté sous forme d'arbre. Le deuxième algorithme a pour but de renforcer les liens entre les individus au sein du réseau social de manière aléatoire représentant l'ajout des amis qui ont les mêmes centres d'intérêt, on choisit le coefficient rho d'arêtes aléatoires que l'on désire. Le troisième algorithme permet de renforcer une nouvelle fois les liens mais cette fois ci non pas de manière aléatoire mais avec des nœuds voisins, qui seraient représentés par des amis d'amis dans un réseau social.

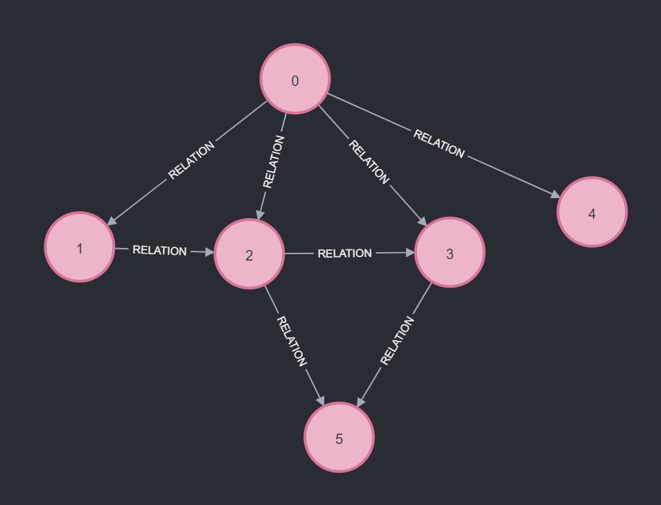
Une fois les trois algorithmes réalisés, on obtient un graphe avec un coefficient d'arêtes aléatoires par rapport au rho choisi, ces graphes sont affichés sous forme de matrice. On peut ensuite visualiser le graphe sur neo4j grâce à la fonction create_graphe(G).

création d'un graphe aléatoire de n nœuds et de n liaisons

def graphe(nbNoeuds):
    G = { "V": [], "E": []}
    existe = True
    test = 0
    for i in range(1,nbNoeuds + 1):
        G["V"] = G["V"] + [i]

    for i in G["V"]:
        a = randint(1,i)
        test = 0
        existe = True
        while existe == True:
            test = 0
            compteur = 0 
            for j in G["E"]:
                compteur = compteur + 1 
                if j == [a,i] or j == [i,a] or i == a :
                    a = randint(1,i)
                else:
                    test = test + 1
            if test == compteur:
                existe = False
        G["E"] = G["E"] + [[i,a]]

    return G

Renforcement des liens avec rho % d'arêtes aléatoires

def renforcement_Graphe(G,rho,E):
    limite = rho*(E - (len(G["E"])))
    nU = []
    for t in G["V"]:
        nU = nU + [t]
    i = 0

    while i<limite and len(nU)>0:
        u = random.choice(nU)
        nV = []
        for a in G["V"]:
            nV = nV + [a]
        nV.remove(u)
        arêtecréée = False

        while len(nV)>0 and arêtecréée == False :
            compteur = 0
            test = 0
            v = random.choice(nV)
            nV.remove(v)
            for j in G["E"]:
                test = test + 1
                if j == [u,v] or j == [v,u]:
                    compteur = compteur 
                else:
                    compteur = compteur + 1
            if compteur == test:
                G["E"] = G["E"] + [[u,v]]
                i = i + 1
                arêtecréée = True
        if arêtecréée == False:
            nU.remove(u)
    return G

Renforcement des liaisons

def renforcement2(G,E):
    limite = E - len(G["E"])
    n = []
    for t in G["V"]:
        n = n + [t]
    i = 0
    voisins = []
    test = 0
    compteur = 0

    while i<limite and len(n)>0:
        u = random.choice(n)
        for k in range(len(G["E"])):
            for j in range(len(G["E"][k])):
                if G["E"][k][j] == u:
                    if j == 0:
                        voisins = voisins + [G["E"][k][1]]
                    else :
                        voisins = voisins + [G["E"][k][0]]           

        arêtecréée = False
        while len(voisins)>0 and arêtecréée == False:
            v = random.choice(voisins)
            voisins.remove(v)
            for w in voisins:
                test = 0
                compteur = 0
                for j in G["E"]:
                    test = test + 1
                    if j == [v,w] or j == [w,v]:
                        compteur = compteur 
                    else:
                        compteur = compteur + 1
                if compteur == test:
                    G["E"] = G["E"] + [[v,w]]
                    i = i + 1
                    arêtecréée = True
                
        if arêtecréée == False:
            n.remove(u)
    return G

Créer les graphes dans neo4j

def create_graphe(G):
    """ Creation du graph G dans neo4j """

    edges = G.get("E")
    vertices = G.get("V")
    
    with driver.session(database="neo4j") as session:
        #1- creation des sommets 
        for vertex in vertices :
            session.write_transaction(create_node, vertex)

        #2- creation des relations
        for edge in edges :
            session.write_transaction(create_relation, edge[0], edge[1])

    print("Graph created successfuly!")



def create_relation(tx, no1, no2):
    """ creattion d'une relation entre deux noeuds """

    cypher= """MATCH (n1:NODE), (n2:NODE)
            WHERE n1.no = $no1 AND n2.no = $no2
            MERGE (n1)-[r:RELATION]-(n2)
            RETURN n1,r,n2"""
    #2- execution de la requete 
    result = tx.run(cypher,no1=no1,no2=no2)
    #3- retour du res
    return result
    

def create_node(tx, no):
    """ tx tarnsaction appelee """
    #1 - requete cypher
    cypher = "CREATE (n:NODE) SET n.no = $no RETURN n"
    #2- execution de la requete 
    result = tx.run(cypher,no=no)
    #3- retour du res
    return result 

Analyse du graphe créé

Une fois le graphe créé il faut effectuer des tests dessus pour vérifier que le graphe obtenu correspond bien à un réseau social. Un réseau social est caractérisé par la taille moyenne des chemins ainsi que par son coefficient de clustering.

La taille moyenne des chemins d'un graphe est le nombre moyen des chemins pour relier un nœud à un autre.

Le coefficient de clustering d'un graphe aussi appelé coefficient d'agglomération est une mesure de regroupement des nœuds dans un réseau. Ce coefficient varie de 0 et 1, il représente la probabilité que deux nœuds soient connectés sachant qu'ils ont un voisin en commun, ce qu'on appel la transitivité. Lorsque le coefficient est à 0, le graphe forme un arbre alors que lorsque le coefficient est à 1, le graphe est un graphe complet, c'est à dire que tous les nœuds sont reliés les uns aux autres. 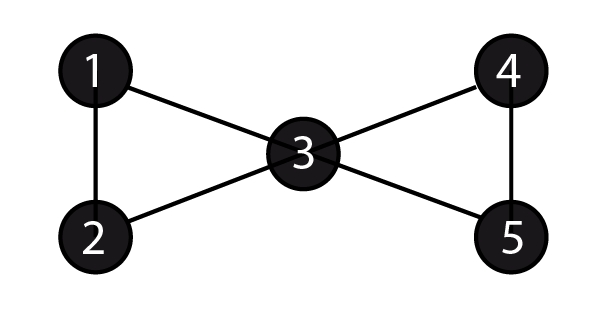On peut obtenir le coefficient de clustering grâce à la formule suivante : (nombre de triangles X 3 / nombre de triades connexes) Par exemple dans le cas du schéma ci-dessous, il y a deux triangles et dix triades connexes (123,231,312,345,453,534,135,134,234,235). On obtient donc un coefficient de clustering égal à 0.6 (6/10).

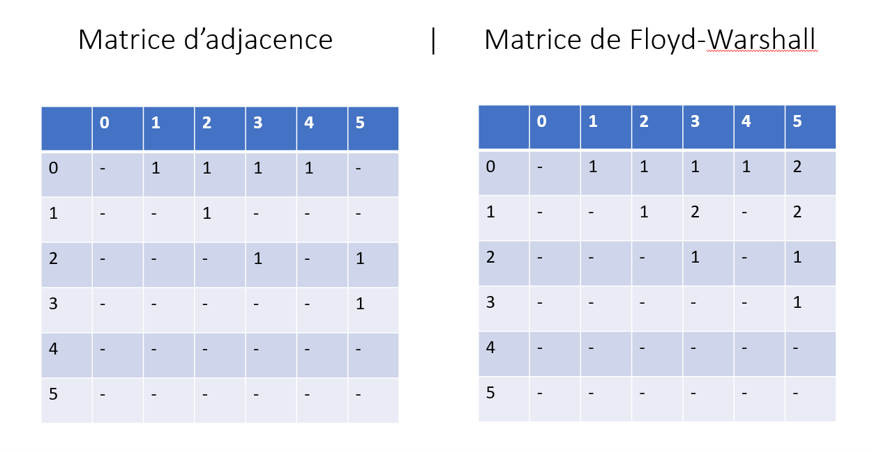
On va donc utiliser des algorithmes pour obtenir ces différentes valeurs. On ne peut pas directement les appliquer, il faut donc utiliser l'algorithme de Floyd-Warshall. Floyd-Warshall prend en entrée une matrice d'adjacence et renvoi en sortie une matrice qui regroupe tous les plus courts chemins pour relier un nœud à un autre. Le principe de Floyd-Warshall est simple, il suffit de parcourir la matrice d'adjacence et de regarder si deux nœuds peuvent être reliés entre eux par l’intermédiaire d’un autre nœud, si oui on change la valeur dans la matrice par le nombre de nœuds parcourus pour atteindre l’objectif si cette valeur est inférieure à la valeur initiale. Une fois cet algorithme réalisé sur la matrice d'adjacence initiale, on obtient une matrice des plus courts chemins. On peut ensuite appliquer le coefficient de clustering et la taille moyenne des chemins sur cette matrice obtenue.

Dans le cas du graphe suivant, on a une matrice d'adjacence avec la taille des chemins et les "-" représentant les chemins impossibles, puis on obtient à partir de celle-ci la matrice de Floyd-Warshall qui permet de montrer des liens entre deux nœuds qui n'ont pas de lien direct.

Algorithme de Floyd-Warshall

def fw_floyd_warshall_k(FW,k):
    """
    intercale k entre chaque couple de sommet 
    """
    #1- matrice k-1
    M0 = FW["M"]
    P0 = FW["P"]

    #2 - matrices de sortie pour k
    M = []
    P = []
    
    nbl = len(M0)
    nbc = len(M0[0])

    #3- iteration sur la matrice d'adjacence k-1
    for i in range(0, nbl):
        Ml = []
        Pl = []
        for j in range(0, nbl):
           
            #4- chemin à minimiser  
            mij = M0[i][j]
            pij = P0[i][j]

            #5- nouveau chemin a considerer par le sommet k
            mik = M0[i][k]
            mkj = M0[k][j]
            
            #print("mij: " + str( mij ) +" mik: " + str(mik) + " mkj: " + str(mkj) )

            #6- si le chemin par k optimise le chemin a k-1 on le met
            # à jour dans la nouvelle matrice

            if fw_supp(mij, mik, mkj):
                Ml += [ mik + mkj ]
                Pl += [k]
            else :
                Ml += [mij]
                Pl += [pij]
                    
        M += [Ml]
        P += [Pl]
    
    return { "M":M, "P":P }

def fw_floyd_warshall(FW0):
    """
    Apllique l'algorithme de FW sur la matrice initiale pour trouver
    les plus courts chemin pour tous couple de sommets
    """
    
    M = FW0["M"]
    nbv = len(M)
    FW = FW0; 
    
    #intercale v entre chaque couple de sommet
    for k in range(0, nbv) :
        FW = fw_floyd_warshall_k(FW, k)
        
    return FW

Algorithmes d'analyse du graphe

Coefficient de clustering

 
def fw_neighbor(n, FW):
    """ Recupere les voisins a->b = 1 dans la matrice d'adjacence """
    M = FW["M"]
    pth = M[n]
    nbv = len(M)
    nei = []
         
    for v in range(0,  nbv):
        if pth[v] == 1 :
            nei += [v]

    return nei

def fw_nei_inter(nei, vnei):
    """
    intersection entre deux liste pour trouver
    la les voisins conecté entres eux
    """
    return [value for value in nei if value in vnei]
   

def fw_connected_neighbor(nei,FW):
    """
    calcul le nombre de voisin de la liste des voisins
    sont connectés entre eux
    """
    nbv = len(nei)
    M = FW["M"]
    cnei = 0 #nb de voisin connectes
    
    for i in range(0, nbv):

        #1- ieme sommet de la liste des voisins
        v = nei[i]

        #2- les voisin du sommet v 
        vnei = fw_neighbor(v, FW)

        #3-intersection entre la liste des voisins et le voisins de v
        vnei_in_nei = fw_nei_inter(nei, vnei)

        #4- nombre de voisin connectés entre eux
        cnei += len(vnei_in_nei)

    return cnei



def fw_clustering_local( v, FW ):
    """
    Rapport entre le nombre de lien entre le nombre de voisins conectés entre eux
    et le nombre max kv de connexion entre voisin du sommet v
    """
    nei = fw_neighbor(v, FW)
      
    #2- calcul le nombre de voisins connectés entre eux
    cn = fw_connected_neighbor(nei,FW)

    #3- calcul du coeff local 1 / ( kv * (kv - 1)) * cn
    kv = len( nei )
    if kv < 2 :
        cl = 0
    else :
        cl = ( 1 / ( kv * (kv - 1) / 2 ) ) * cn

    return cl
    

def fw_clustering_coeff(FW):

    #1- recupere les voisins
    M = FW["M"]
    nbv = len(M)
    SUM_CL=0 #clustering global 
    
    for v in range(0, nbv):
        cl = fw_clustering_local( v, FW )
        SUM_CL += cl
       
    #2- moyenne
    AV_CLG = SUM_CL / nbv
    return AV_CLG

Taille moyenne des chemins

def fw_average_path_length(FW):

    APL = 0
    SPL = 0 #sum path length  
    NBP = 0 #number path

    #1- recupere la matrice des plus courts chemins
    M = FW["M"]
    nbv=len(M) 
    nbp=0 #nombre de chemin 

    for i in range(0, nbv):
        for j in range(0, nbv):
            pl = M[i][j] #path length i = j  => 0
            if pl > 0 :
                SPL += pl
                NBP += 1

    
    APL = SPL /  NBP 
        
    return APL

Création des graphes grâce aux algorithmes

Avec tous les algorithmes décrits ci-dessus, on va créer un graphe puis analyser la taille moyenne du graphe obtenu ainsi que son coefficient de clustering.

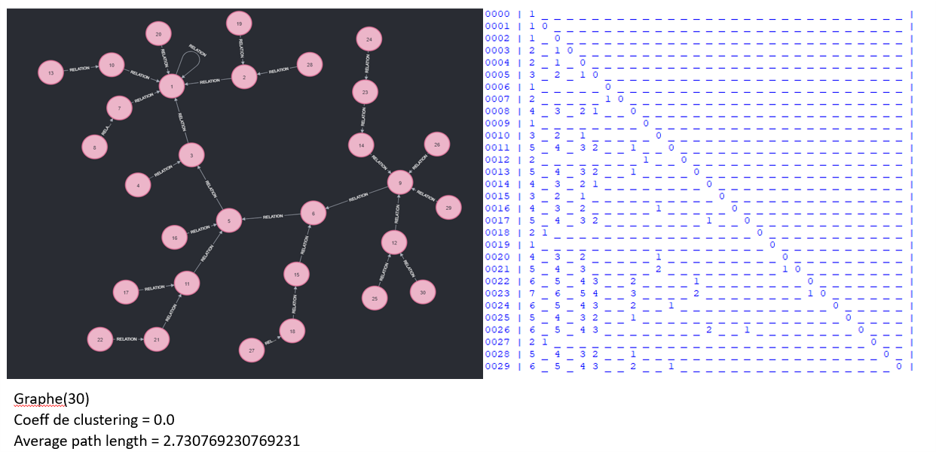
On commence par créer un graphe de 30 nœuds ainsi que 30 liaisons à l'aide du premier algorithme de création du graphe. On obtient donc un graphe sous forme d'arbre, cela représente l'invitation dans le réseau social d'un nouvel individu, chaque individu rejoint le réseau grâce à l'invitation d'un personne. On obtient ensuite le coefficient de clustering et la taille moyenne des chemins grâces aux algorithmes ci-dessus. On peut voir que le coefficient de clustering est à 0 étant donné que le graphe est un arbre et qu'il n'y a aucun triangle qui se forme dans le graphe. La taille moyenne des chemins quand à elle est d'environ 2.7 ce qui est très faible mais c'est expliqué par le fait qu'il n'y ait pas beaucoup de personnes au sein du réseau donc le chemin pour rejoindre une personne est lui aussi faible. On peut également voir la matrice de Floyd-Warshall qui regroupe les plus courts chemins à coté du graphe.

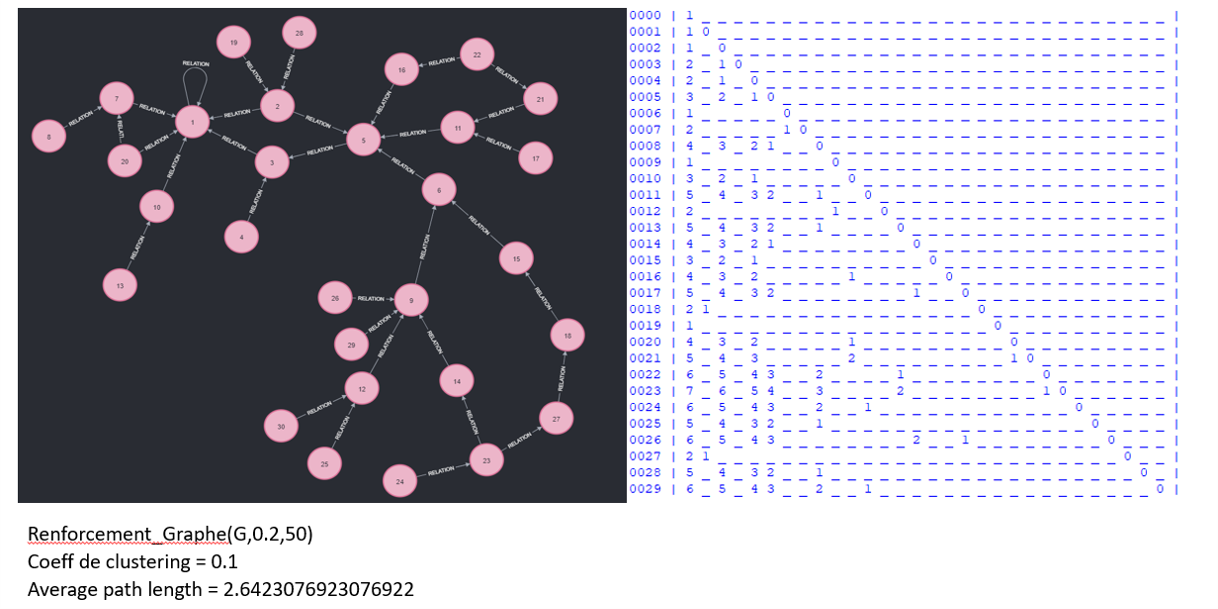
La deuxième étape de la création d'un réseau social consiste à renforcer les liaisons avec un pourcentage d'arêtes aléatoires. Dans notre cas, j'ai renforcé le graphe pour arriver à 50 arêtes mais j'ai mit un coefficient de 0.2, ce qui signifie qu'il y a seulement 20*0.2 arêtes supplémentaires qui vont êtres crées, soit 4 arêtes. Cette étape représente l'ajout en ami de personnes aux sein du réseau par rapport aux centres d'intérêts, ils sont représentés de manière aléatoire sur ce graphe. On peut donc voir que le coefficient de clustering a augmenté étant donné qu'on a rajouté des liaisons internes au graphe sans rajouter de nœuds. La taille moyenne des chemins quand à elle à légèrement diminué mais vu qu'elle était déjà très faible, on ne peut pas voir une grande différence.

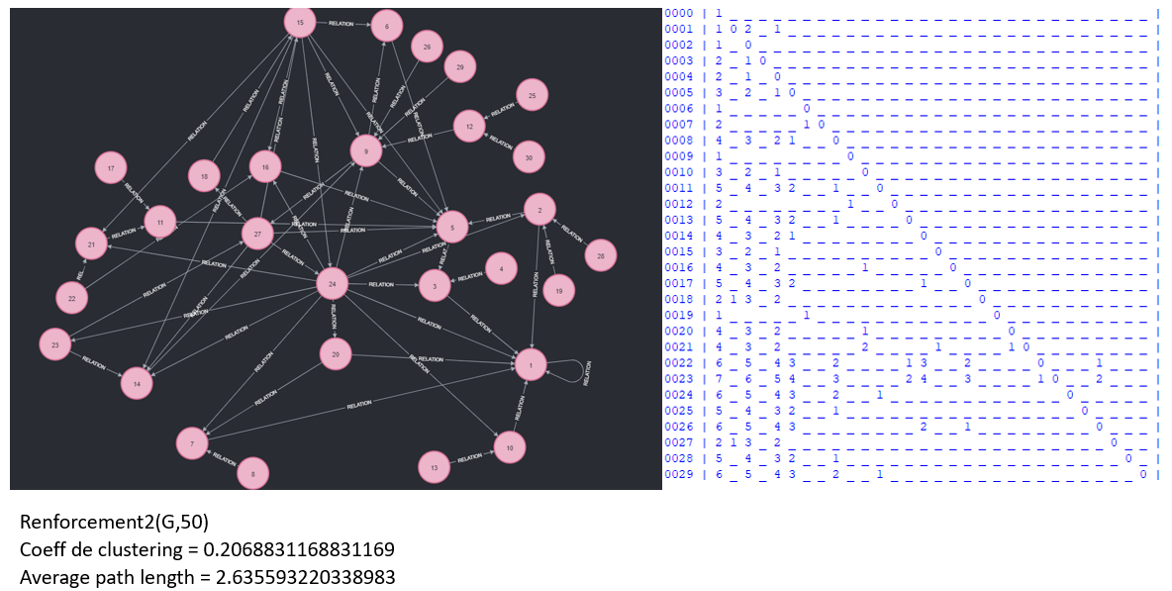
La troisième étape quand à elle permet de renforcer les liens au sein du réseau social en fonction du nombre aléatoire d'arêtes ajoutées à l'étape précédente. Dans notre cas, on a ajouté 4 arêtes aléatoires, nous avons donc actuellement 34 arêtes et nous voulons atteindre 50 arêtes, nous allons donc rajouter 16 arêtes. Ces arêtes vont êtres créer entre voisins ce qui représente l'ajout d'amis d'amis via les recommandations dans un réseau social. Le coefficient de clustering augmente donc une nouvelle fois car il y a une augmentation des liaisons sans augmentation des nœuds et la taille moyenne des chemins reste similaire mais baisse légèrement.