Où placer une (ou plusieurs) antennes 5G dans un village ?

Élève : Briffod Nils

Tuteur : Dorin Bucur

Introduction

Au travers de ce sujet, nous allons réfléchir, réaliser un model mathématique puis le mettre en pratique grâce aux outils informatiques. Nous parlerons de graphes et d'optimisation de longueurs.

Problématique

En quoi consiste ce problème mathématique relié à un exemple concret ? Supposons que dans un village où les maisons sont uniformément réparties, un opérateur téléphonique souhaite installer des antennes. Nous cherchons à minimiser la distance moyenne entre chaque maison et l'antenne 5G. Autrement dit dans une surface donnée, de forme quelconque, nous devons être capables de trouver les coordonnées optimales du point où l'antenne y sera placée. Bien que cette question à été simplifiée, elle repose sur un concept mathématique important notamment au sujet de la planification économique.

Démonstration

Comment déterminer le point où la distance moyenne entre la position de l'antenne et tous les autres points de la figure ?

Cette question a été abordée dans un article de recherche par Morgan F. & Bolton R. (2002) publié dans une revue scientifique, lien de l'article

On commence par un modèle très simple : quatre maisons sont positionnées aux sommets d'un rectangle et on va démontrer que la position optimale d'une antenne est au centre du rectangle. La justification sera donnée par un raisonnement mathématique, basé sur l'analyse de la variation d'une fonction.

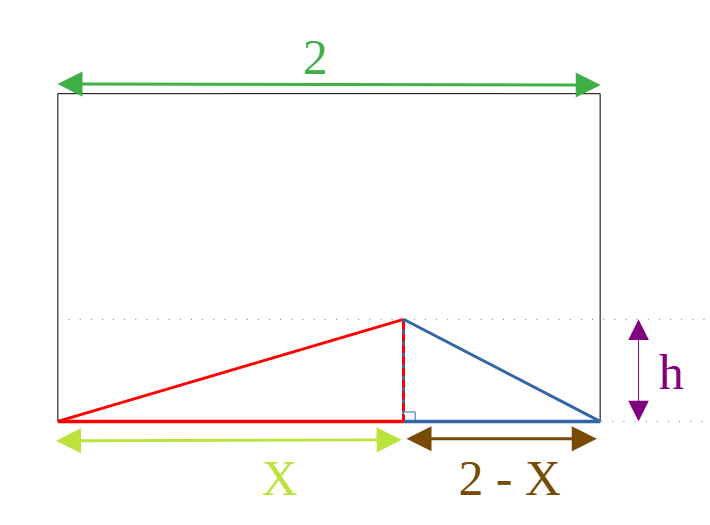
Nous sommes dans un rectangle, comme dans la Figure 1. Nous cherchons a diminuer la somme des longueurs des hypoténuses des deux triangles rectangles (le rouge et le bleu) tout en déplaçant le point A horizontalement.

Figure n° 1

Concentrons nous sur les triangles rectangles. Nous allons déterminer grâce au théorème de Pythagore les longueurs des hypoténuses des triangles:

• Le triangle rectangle rouge a pour longueur de coté : $x$, $h$ et pour hypoténuse : ${\sqrt {x^{2}+h^{2}}}$.
• Le triangle rectangle bleu a pour longueur de coté : $2-x$, $h$ et pour hypoténuse : ${\sqrt {(2-x)^{2}+h^{2}}}$.

Nous allons faire varier $x$ et observer là où la fonction somme est au minimum. Définissons notre fonction somme : $f(x)={\sqrt {(2-x)^{2}+h^{2}}}+{\sqrt {x^{2}+h^{2}}}$.
Nous allons démontrer que pour tout $x$, $f(x)\geq 2{\sqrt {1^{2}+h^{2}}}$, avec égalité lorsque $x=1$:

On souhaite minimiser $f(x)$, ce qui revient a chercher quand sa dérivé s'annule.

$f'(x)=-{\frac {2-x}{\sqrt {(2-x)^{2}+h^{2}}}}+{\frac {x}{\sqrt {x^{2}+h^{2}}}}=0$

${\frac {x}{\sqrt {x^{2}+h^{2}}}}={\frac {2-x}{\sqrt {(2-x)^{2}+h^{2}}}}$

${\frac {x^{2}}{x^{2}+h^{2}}}={\frac {(2-x)^{2}}{(2-x)^{2}+h^{2}}}$

$x^{2}(2-x)^{2}+x^{2}h^{2}=(2-x)^{2}x^{2}+(2-x)^{2}h^{2}$

$x^{2}h^{2}=(2-x)^{2}h^{2}$

$x^{2}=(2-x)^{2}$

$x^{2}=4-4x+x^{2}$

$0=4-4x$

$4x=4$

$x=1$

Ainsi la somme est la plus base lorsque $x=1$. On en conclut que $f(x)\geq 2{\sqrt {1^{2}+h^{2}}},\forall x\in \mathbb {R}$, avec égalité pour $x=1$

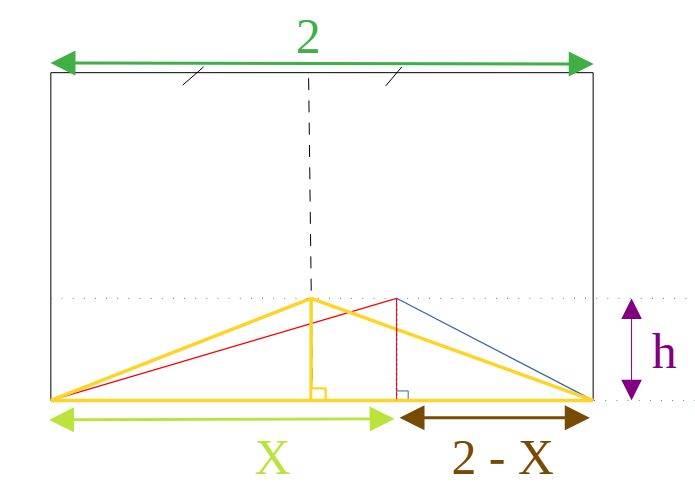
Ainsi nous avons démontré que la somme des distances est la plus basse lorsque $x$ vaut la moitie de la base du triangle comportant les deux triangles rectangles. Ce qui devient le triangle jaune dans la Figure 2.

Figure n° 2

Le même argument s'applique pour la somme des distances aux maisons M3 et M4. En une deuxième étape, le même argument est appliqué pour la somme des distances de A aux maisons M2 et M3, respectivement M1 et M4, justifiant ainsi que la position optimale et au centre du rectangle.

Nous venons ainsi de démontrer où se trouve le point minimisant la distance moyenne à quatre points dans un rectangle.

Dans la suite, nous souhaitons proposer une méthode numérique pour trouver la position optimale, dans des cas généraux. Cette méthode est basé sur l'analyse du gradient.

Gradient

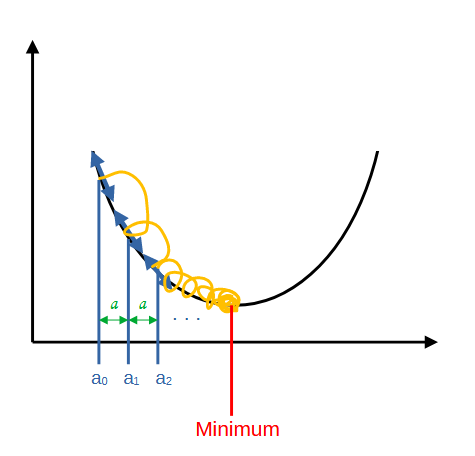
Affin d'illustrer la méthode du gradient, imaginons que nous souhaitons minimiser une fonction convexe à une variable.

Nous allons alors prendre un point aléatoire sur la courbe (a0), puis l'on calcule la pente de la courbe à ce point, on utilise alors la dérivée (si notre fonction à minimiser prend plusieurs paramètres alors on calcule les dérivées partielles pour chacun des paramètres). Le calcul de cette dérivée nous donne la direction de la pente, puis on avance d'un petit pas nommé alpha dans la direction de la descente. Ce qui nous amène à une seconde position (a1) et on recalcule la dérivée en répétant la procédure, jusqu'avoir convergé au minimum de notre fonction.

Figure n° 3

Où situer une antenne 5G dans un village ?

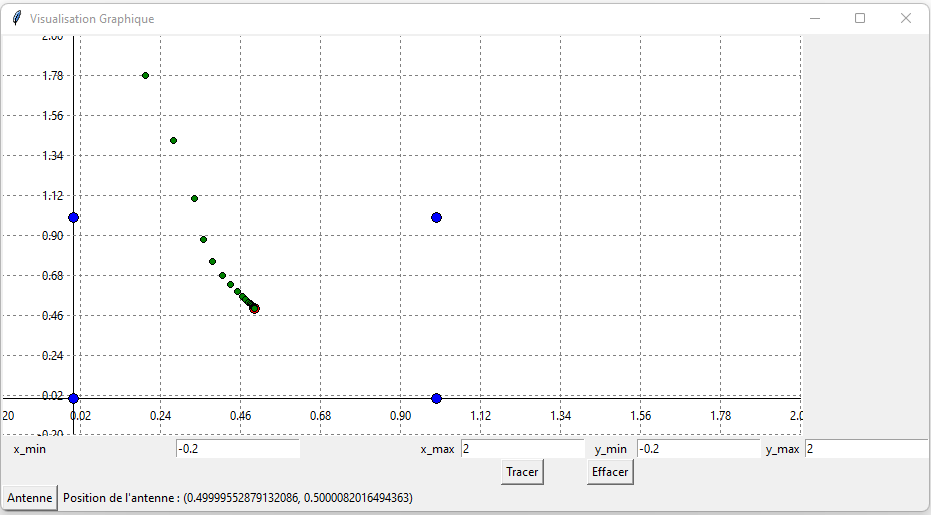
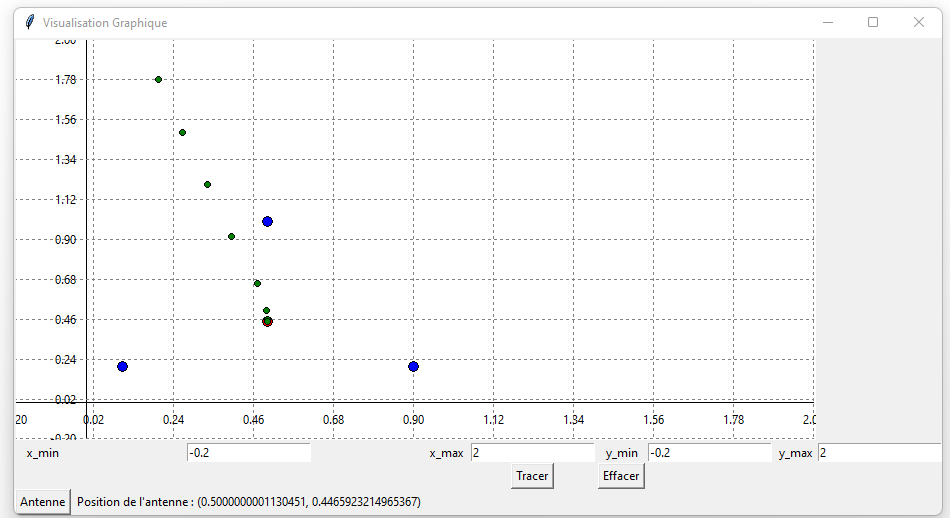
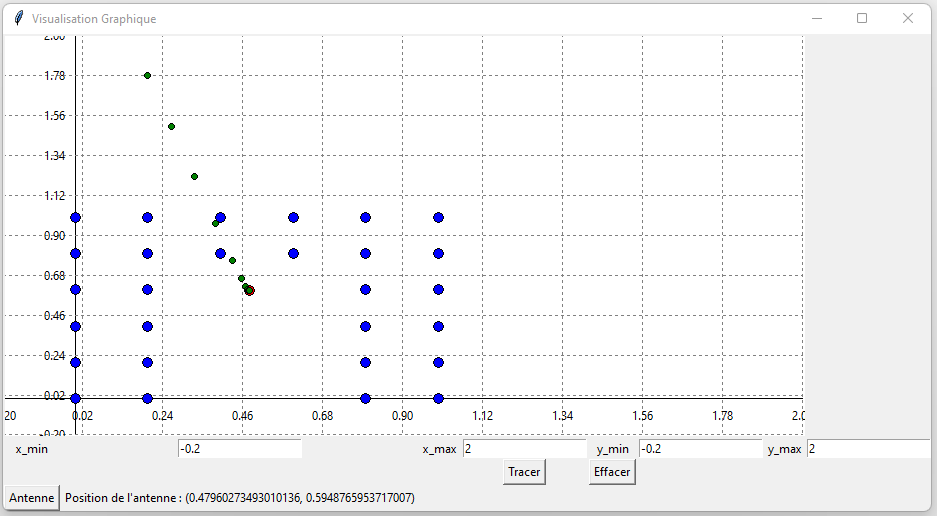
Ainsi l'on peut écrire un algorithme qui permet de trouver le point de l'antenne qui minimise la distance moyenne dans un village qui peut avoir une forme géométrique générale. Petite information a noter alpha doit être choisis judicieusement puisqu'on pourrait directement au bout de quelques itérations de la boucle dépasser le minimum, ce qui m'avait poser des problèmes.

Exemple de la méthode du gradient avec différentes figures :

Diagramme de Voronoï

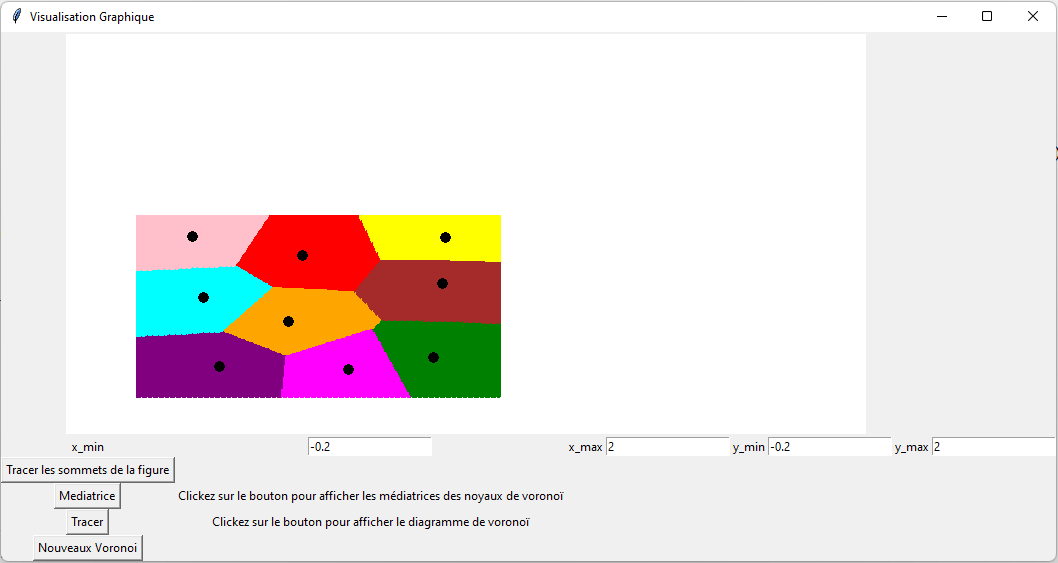
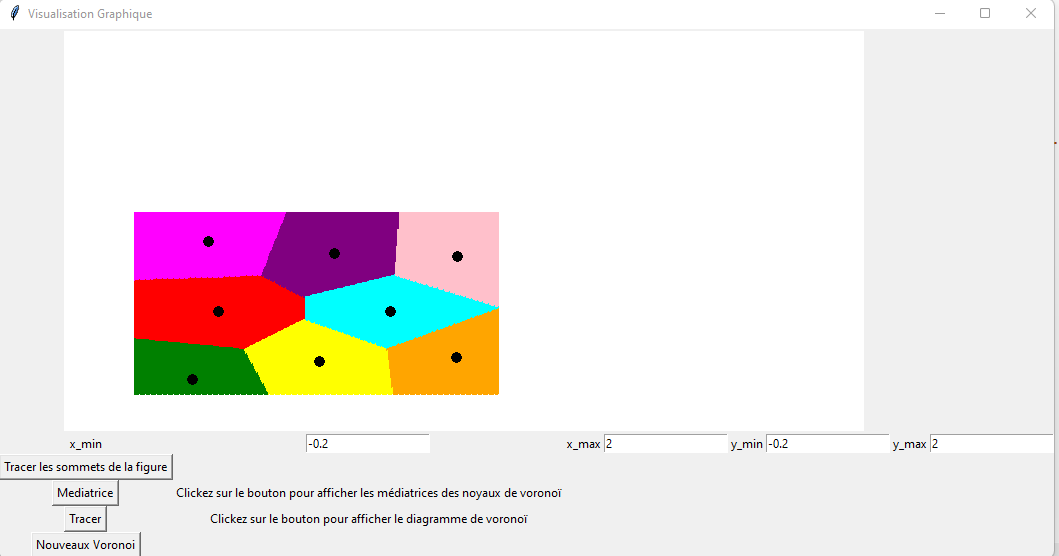
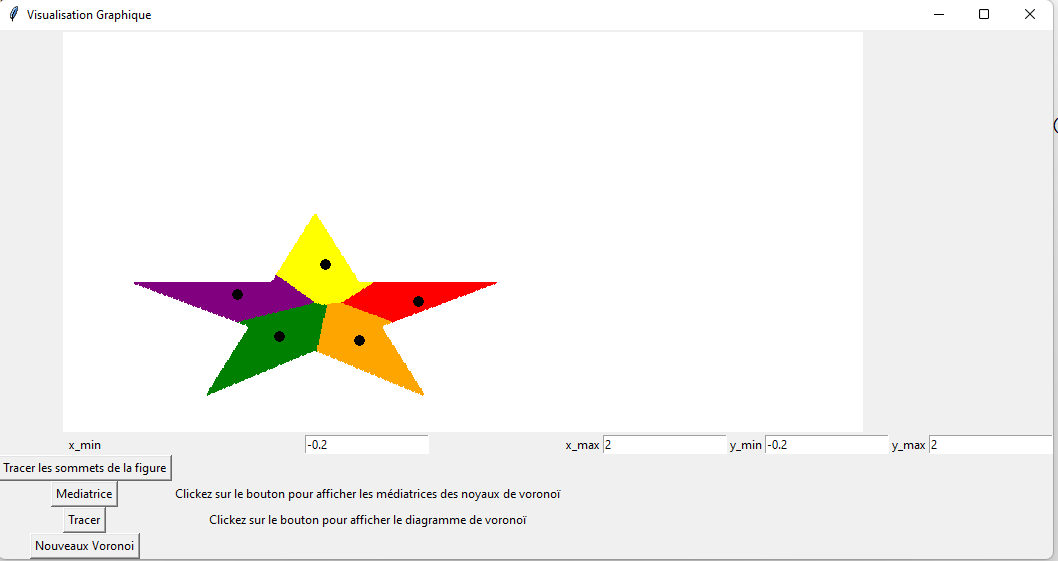
Le diagramme de Voronoï est une division en "cellules" d’un plan, basée sur un ensemble de points donnés (les antennes, dans cet exemple). Chaque cellule contient tous les points du plan qui sont les plus proches d’une antenne par rapport aux autres.

Ce diagramme est utilisé en géométrie, en cartographie, en biologie, et dans de nombreux autres domaines, notamment pour modéliser des zones d’influence.

Imaginons maintenant que nous ayons 2, 3 ou 4 antennes 5G déjà positionnées dans notre village. Si chaque maison se connecte à l’antenne la plus proche, alors un diagramme de Voronoï apparaîtrait naturellement.

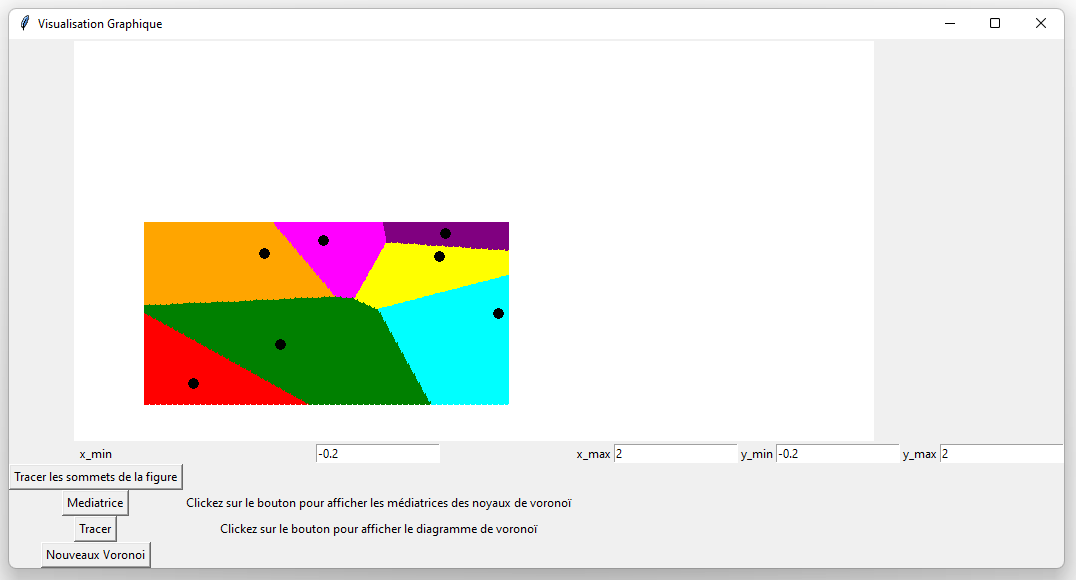
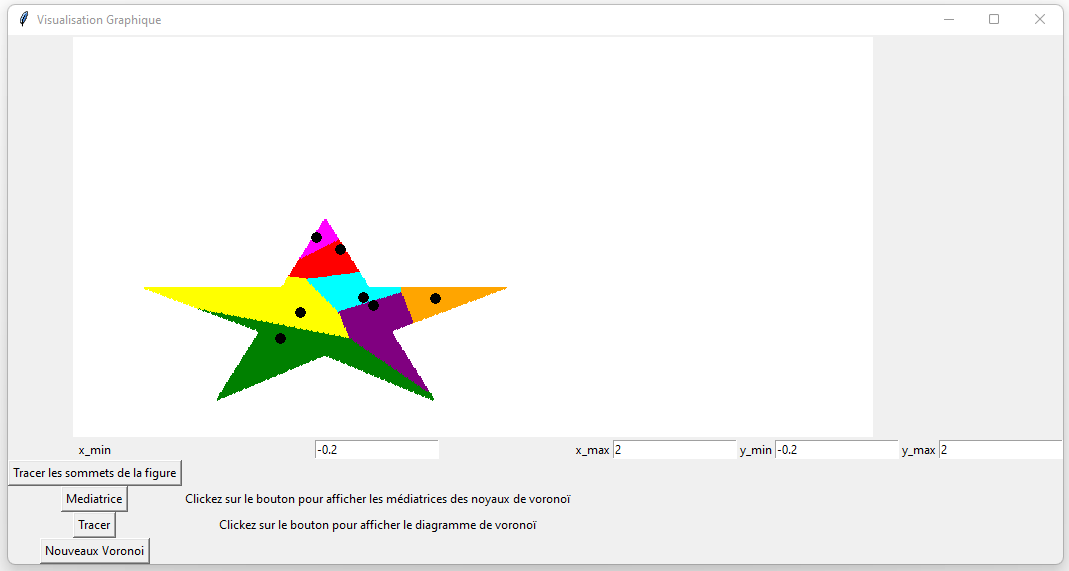
J'ai ainsi mis en œuvre un algorithme permettant de réaliser des diagrammes de Voronoï peu importe la forme de la figure, de manière naïve sans optimisation. Les antennes 5G sont représentées par les points noirs. Les antennes ont été placées de manière aléatoire dans le village affin de pouvoir observer à quoi ressemble un diagramme de Voronoï. De plus j'ai modifié la forme du village pour observer différents exemples.

Dans ce cas, toutes les maisons situées dans une cellule de couleur sont plus proches de l'antenne dans leur cellule que de n'importe quelle autre.

Il est important de noter que les frontières entre les cellules ne sont pas linéaires, elles sont en escalier. Cela est du à la représentation graphique, à la représentation numérique (calcul sur des flottants) et à la densité des points sur le graphique. Par soucis d'efficacité j'ai choisi le meilleur rapport densité/temps de calcul.

• Si les points (antennes) sont bien placés — c’est-à-dire répartis de manière optimale (pas verticalement) par rapport à la distribution des maisons — alors :
  • Les cellules de Voronoï deviennent plus petites et plus équilibrées ;
  • Chaque antenne couvre une zone plus compacte ;
  • Les maisons sont donc plus proches de leur antenne ;
  • Résultat : une meilleure efficacité de couverture.

Où situer plusieurs antennes 5G dans un village ?

C'est une bonne chose de pouvoir observer quelle région se connecte à quelle antenne, mais il faut à présent bien placer les antennes.

Je n'ai pas réussi à mettre en œuvre une méthode de gradient (2 dérivées partielles par antenne). Par conséquent, je me suis orienté vers un autre algorithme : Le Recuit Simulé.

Pourquoi avoir choisis cet algorithme ? L'avantage principale de cet algorithme c'est qu'il à été conçu pour éviter d'être bloqué dans un minimum local. Malheureusement l'algorithme baisse en précision et on ne peux pas être sûr que le résultat soit optimal.

C'est pour ça que je vous invite à comparer les résultats du carré avec des résultats prouvés mathématiquement par Morgan F. & Bolton R: lien de l'article

Comment fonctionne le Recuit Simulé ?

• On génère $n$ antennes de manière aléatoire dans la figure -> antenne initiale.
• On calcule le coût, ici la distance moyenne de chaque maison à l'antenne.

On boucle les étape suivantes pour chaque itération :

• On perturbe la solution, on déplace une antenne au hasard d'un petit pas dans le village.
• On calcule le nouveau coût
• Si le nouveau coût est meilleur, on garde le changement
• Sinon on accepte parfois le changement avec une probabilité de garder la modification qui diminue avec le temps, ce qui permet de ne pas rester bloquer dans un minimum local.
• puis l'on arrête si l'on a pas trouvé mieux depuis longtemps, où après un nombre d'itération maximal.

On notera que les points ne sont pas optimaux, cela est du à l'algorithme utilisé, à la représentation graphique, à la représentation numérique (calcul sur des flottants) et à la densité des points sur le graphique. Par soucis d'efficacité j'ai choisis le meilleur rapport densité/temps de calcul.

Exemple de la répartition de 6 antennes dans un carré au fur et à mesure des itérations :

Organisation optimale des antennes

Si l'on fait tourner cet algorithme avec de plus en plus d'antennes, l'on remarquera que les antennes seront disposées de manière hexagonale, est-ce un hasard ?

Dans un contexte de pavage optimal du plan, l’hexagone régulier est la forme géométrique qui minimise le rapport entre le périmètre total et la surface couverte lorsqu’un grand nombre de cellules identiques doivent remplir un plan sans chevauchement ni intersection. Ce résultat est formalisé par le théorème du nid d’abeille, démontré rigoureusement par Thomas C. Hales en 2001, qui prouve que parmi toutes les divisions possibles du plan en cellules de surface égale, le pavage hexagonal possède le périmètre total minimal. Ce principe explique pourquoi les structures naturelles comme les alvéoles des abeilles adoptent une organisation hexagonale. De manière analogue, en télécommunications, une disposition hexagonale des zones de couverture des antennes optimise l’efficacité de couverture, réduit les zones mortes et uniformise la répartition des ressources réseau sur une large surface, ce qui est essentiel dans la conception des réseaux cellulaires.

Thomas C. Hales (2001), The Honeycomb Conjecture, Discrete & Computational Geometry, vol. 25, pp. 1–22, DOI: 10.1007/s004540010071.

Conclusion

Pour placer des antennes dans un village, il faut les positionner de manière à minimiser les zones sans couverture (dans le cas où l'on ajouterait une distance maximum pour se connecter à une antenne) tout en répartissant les antennes uniformément, idéalement selon un motif hexagonal pour maximiser l’efficacité et la compacité.

Source

Descente de Gradient
Série de vidéos sur le Recuit Simulé
Références jointes au sujet