Pavages de Penrose
Bien qu'étant utilisés depuis des siècles, ce n'est que tout récemment que l’engouement pour leurs études a eu lieu (durant la seconde moitié du 20eme siècle).
Nous devons ces études à plusieurs grands noms des mathématiques, tels que wang, robinson ou encore Penrose. C'est aux travaux de l'un de ces mathématitiens que nous nous intéresserons dans les lignes qui suivent.
Introduction à la notion de pavage
La notion de pavage et ses propriétés les plus classiques sont fondamentales.
Définition(s) d'un pavage
Un pavage est formé d'un ensemble fini de pièces (compacts) dont l'on peut disposer en quantité infinie, afin de paver un plan selon plusieurs règles :
-Il ne doit pas y avoir d’interstice
-Il ne doit pas y avoir de chevauchement entre les différents compacts
-Le pavage doit paver un plan (donc s'étendre à l'infini)
On peut pour cela utiliser une caractérisation un peu plus mathématique. Car, bien que les pavages de penrose soient en 2D, il serait tout à fait possible de réaliser un pavage en 3D.
Cette caractérisation est la suivante :
Soit E un espace topologique. On appelle pavage tout ensemble p de compacts de E tel que
(i) U(p∈P) P = E , (recouvrement de l'espace)
(ii) pour tout p,q∈ P, °p ∩ °q= ∅ (pas de chevauchement)
(iii) pour tout K ⊂ E compact, {p ∈ P | P ∩ K != ∅} est fini (recouvrement local)
Néanmoins cette définition est incomplète puisqu'elle ne précise pas qu'il doit y avoir un nombre fini de type de compact.
Notion de périodicité et d'apériodicité
Un pavage est dit périodique lorsque l'on retrouve un motif avec lequel on peut, par translation ou rotation , paver le plan.
Un pavage est dit aperiodique lorsque l'on ne peut pas reconnaitre de motif récurent par translation ou rotation sur l’entièreté du plan.
On a souvent pensé, comme le montre la conjecture de Wang, qu'avec un jeu de tuile permettant de réaliser un pavage apériodique, on pouvait obligatoirement en réaliser un périodique avec le même ensemble de compacts.
(image tuiles de wang)
Or, c'est dans les années 1950 que le pavage de Robinson, composé de 6 tuiles (donc converties en tuiles de wang, 24), fût démontré comme apériodique et permis donc de réfuter cette idée (et la conjecture de wang).
Les pavages de Penrose
Ces types de pavages sont une découverte de Roger Penrose, et ils ont permis de populariser la notion de pavage et de la rendre "plus grand public"
Roger Penrose
Roger Penrose, né en 1931 en Angleterre est le mathématicien connu pour avoir découvert en 1974 un pavage aperiodique, possédant uniquement 2 types de pièces, nommé par la suite pavage de Penrose.
Les principes d'un pavage de Penrose Kite/Darts
Principe
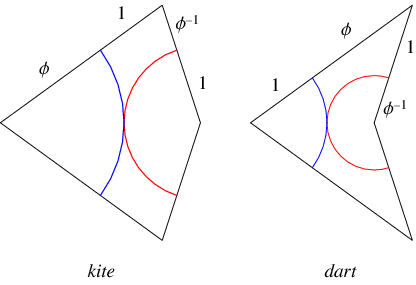
Ce type de pavage de Penrose est composé de deux types de pièces : les kites et les darts .
Le principe essentiel de ce type de pavage de Penrose étant que les deux pièces ne peuvent être assemblées afin de former un losange.
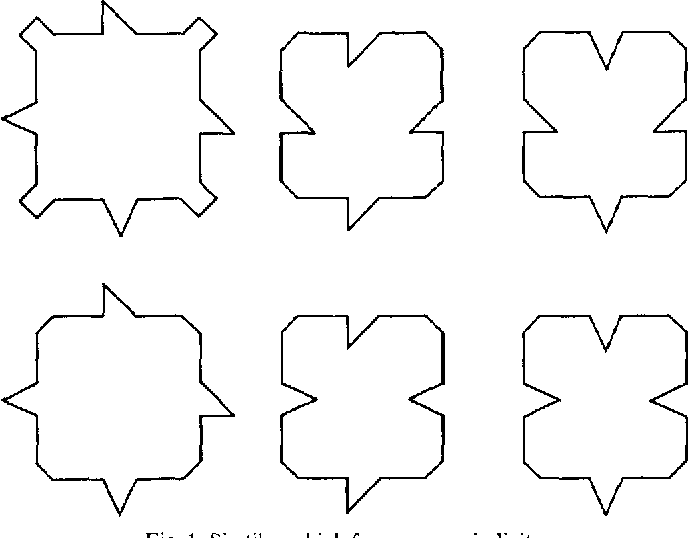
Motifs remarquables
On peut retrouver plusieurs motifs remarquables dans ce type de pavage de Penrose, bien que n'étant pas réguliers ou prévisibles dans leur apparition (puisque le pavage est apériodique).
Les principes d'un pavage de Penrose avec losanges
Ce type de pavage est composé encore une fois de deux pièces mais ici ces deux pièces sont des losanges comportant des angles différents.
Il ne va pourtant dans ce wiki être traité que le cas des kites et des darts, et ce pour une raison simple :
les deux types de pièces sont fortement liées.
En effet, en découpant les losanges, on peut retrouver des kites et des darts, on peut donc plutôt aisément passer d'un pavage à un autre à l'aide d'un simple découpage.
Les méthodes de construction d'un pavage de Penrose
La méthode dite "intuitive"
Cette méthode consiste à placer les pièces "bloquées" (qui ne peuvent aller que là où on cherche à les mettre), puis continuer, et si blocage il y a on enlève l'étape précédente et on tente l'autre possibilité.
Comme on peut aisément le constater,cette méthode était très complexe et très lourde à coder, bien qu'étant fonctionnelle.
La méthode par inflation/déflation
Principe
La méthode par inflation/déflation est une méthode où l'on partage les différentes pièces afin de reformer de nouvelles pièces, plus petites.
Ainsi,si l'on considère le coté d'une pièce comme étant de taille fixe, on peut constater l'augmentation du nombre de pièces qui forment le pavage, et avec un nombre de division qui tend vers l'infini, on peut montrer que le pavage de penrose pave le plan.
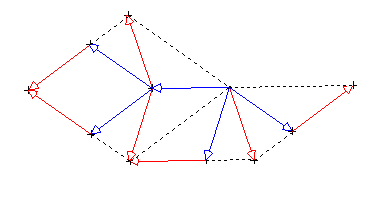
Constuction géométrique
Pour appliquer la méthode par inflation déflation, on divise chaque demi-kite en un kite et un demi dart, et chaque demi-dart en un demi-kite et un demi dart.
Avec cette méthode ci, on peut aisément construire un algorithme qui fonctionne de maniere récursive et qui génère un pavage de Penrose.
Réalisation du code
Le programme permet de générer un pavage de penrose, de la profondeur désirée (nombre de récursivité), il indique le nombre de pièces total ainsi que le niveau de récursivité dans lequel on se trouve.
Le code a été réalisé sur processing, un logiciel libre, le programme est codé en java :
// quelques constantes utiles
float PI=3.14159265; // merci archimède !!
float PIsur5=PI/5; // l'angle générateur de base
float epsilon = 1E-5; // defini les points proches
// Les tailles écran
int ecranX=800;
int ecranY=800;
int marge =100;
// Les couleurs
color couleurKite = color(255, 204, 0); // jaune
color couleurDart = color(0, 255, 0); // vert
color couleurTrait = color(255, 255, 255); // blanc
int profondeur = 10; //profondeur
int attente = 1000;//750;// en ms
// Les variables globalse
int nbForme=0;
// definition des classes graphiques
// ************************************
// un point en memoire
class pointMem
{
private float x;
private float y;
// Le createur
public pointMem(float Xd, float Yd)
{
x=Xd; // putX(Xd);
y=Yd; // putY(Yd);
}
// Le createur par defaut
public pointMem()
{
x=0;
y=0;
}
// Les méthodes de manipulation des attributs
public float getX() {
return x;
}
public float getY() {
return y;
}
public void putX(float Xp)
{
x=Xp;
}
public void putY(float Yp)
{
y=Yp;
}
// manipulations géométriques
// translation
public void translate(pointMem P)
{
putX(getX()+P.getX());
putY(getY()+P.getY());
}
// rotation autour d'un point P et d'angle A
public void rotation( pointMem P, float A)
{ // on ramene au centre
putX(getX()-P.getX());
putY(getY()-P.getY());
// on tourne
float C=cos(A);
float S=sin(A);
putX(getX()*C-P.getY()*S);
putY(getX()*S+P.getY()*C);
// on remet au bon endroit
putX(getX()+P.getX());
putY(getY()+P.getY());
}
// Homothetie de rapport k de centre P
public void homothetie(pointMem P, float K)
{ // on ramene au centre
putX(getX()-P.getX());
putY(getY()-P.getY());
// on amplifie
putX(getX()*K);
putY(getX()*K);
// on remet au bon endroit
putX(getX()+P.getX());
putY(getY()+P.getY());
}
// deux points proches ??
boolean egal(pointMem P1, pointMem P2)
{
return
(abs(P1.getX()-P2.getX())<epsilon) &&
(abs(P1.getY()-P2.getY())<epsilon);
}
// procedures graphiques
public void draw()
{
point(getX(), getY()); // on invoque les procedures de la bibliotheque
}
public void draw(color c)
{
stroke(c); // bascule la couleur
draw();
}
};
// ****************************************************
// exemple de création de points aux coordonnées 0,0
// pour le kite de base
pointMem P1 = new pointMem(0, 0); // reserver un espace memoire de taille pointMem lui affecter le nom de P1 et le remplir de valeurs nulles
pointMem P2 = new pointMem(0, 0);
pointMem P3 = new pointMem(0, 0);
pointMem P4 = new pointMem(0, 0);
// Procedures et fonctions utiles
// Calcul de la norme d'un vercteur
float norme(pointMem P1, pointMem P2) // calcul de la norme du vecteur P1 P2
{
return sqrt(sq(P1.getX()-P2.getX())+sq(P1.getY()-P2.getY()));
}
// trace une ligne
void ligne(pointMem P1, pointMem P2)
{
line(P1.getX(), P1.getY(), P2.getX(), P2.getY());
}
// traitement des demi cerf volants
void demiKite(pointMem P1, pointMem P2, pointMem P3, int n)
{
if (n<=0)
{ // on trace et on "dégage"
// on colorie
fill(couleurKite); // couleur remplissage des formes
stroke(couleurKite);
beginShape();
vertex(P1.getX(), P1.getY());
vertex(P2.getX(), P2.getY());
vertex(P3.getX(), P3.getY());
endShape(CLOSE);
noFill();
stroke(couleurTrait);
ligne (P1, P2);
ligne (P2, P3);
nbForme++;
return;
}
// dans le cas contraire, on traite
// on redecoupe puis on relance !!
// Creation de points intermediares P4 et P5
pointMem P4 = new pointMem(0, 0);
pointMem P5 = new pointMem(0, 0);
// on les calcul
// calcul des coté opposé aux points P1 et P2
float l1=norme(P2, P3);
float l2=norme(P1, P3);
// calcul de la nouvelle longueur de decoupage sur le coté P1 P3
float a= l2/(1+2*cos(PIsur5));
// vecteur (P1 P4) = a/l1 vecteur (P1 P3)
P4.putX(P1.getX()+(P3.getX()-P1.getX())*a/l1);
P4.putY(P1.getY()+(P3.getY()-P1.getY())*a/l1);
// vecteur (P3 P5) = a/l2 vecteur (P3 P2)
P5.putX(P3.getX()+(P2.getX()-P3.getX())*a/l2);
P5.putY(P3.getY()+(P2.getY()-P3.getY())*a/l2);
// On lance la génération suivante suivant le schéma de decoupage
demiKite(P4, P1, P2, n-1);
demiKite(P4, P5, P2, n-1);
demiDart(P3, P4, P5, n-1);
}
// Traitement des demi flèches
void demiDart(pointMem P1, pointMem P2, pointMem P3, int n)
{
if (n<=0)
{ // on trace et on "dégage"
fill(couleurDart); // couleur de remplissage
stroke(couleurDart);
beginShape();
vertex(P1.getX(), P1.getY());
vertex(P2.getX(), P2.getY());
vertex(P3.getX(), P3.getY());
endShape(CLOSE);
stroke(couleurTrait);
noFill();
ligne (P1, P2);
ligne (P2, P3);
nbForme++;
return;
}
// dans le cas contraire
// on redecoupe puis on relance ::
// Creation du point intermediares P4
pointMem P4 = new pointMem(0, 0);
// on le calcul
// calcul des cotés opposés au points P2 et P3
float l2=norme(P1, P3);
float l3=norme(P1, P2);
// vecteur (P1 P4) = l2/l3 vecteur (P1 P2)
P4.putX(P1.getX()+(P2.getX()-P1.getX())*l2/l3);
P4.putY(P1.getY()+(P2.getY()-P1.getY())*l2/l3);
// On lance la génération suivante suivant le schéma de decoupage
demiKite(P3, P4, P1, n-1);
demiDart(P2, P3, P4, n-1);
}
// Les initialisations
void setup()
{
size(800, 800); // taille de l'écran 640 sur x 480 sur y
// Creation du premier demiKite
// a partir des points P1 P3
P1.putX(ecranX-marge);
P1.putY(ecranY/2);
P3.putX(marge);
P3.putY(ecranY/2);
// Calcul du 3ème point P3
// Calcul de la longueur caractéristique du kite
float l2=norme(P1, P3);
// calcul de la nouvelle longueur de decoupage sur le coté P1 P3
float a= l2/(1+2*cos(PIsur5));
float h= (a/2)/tan(PIsur5/2);
pointMem P5= new pointMem(0, 0); // point intermédiaire
// vecteur (P1 P5) = a/2*l2 vecteur (P3 P2)
P5.putX(P1.getX()+(P3.getX()-P1.getX())*a/l2/2);
P5.putY(P1.getY()+(P3.getY()-P1.getY())*a/l2/2);
// vecteur P5 P2 perpendiculaire à P1 P2 avec longueur h
P2.putX(P5.getX()-(P3.getY()-P1.getY())/l2*h);
P2.putY(P5.getY()+(P3.getX()-P1.getX())/l2*h);
// Calcul du 4ème point du kite P4 2ème point du demi kite supérieur
// vecteur P5 P4 perpendiculaire à P1 P2 avec longueur h symétrique par rapport à P2
P4.putX(P5.getX()+(P3.getY()-P1.getY())/l2*h);
P4.putY(P5.getY()-(P3.getX()-P1.getX())/l2*h);
background(0);
stroke(255);
}
int n=0;
boolean sens = true;
void draw() // la procedure cyclique
{
background(0);
demiKite(P1, P2, P3, n);
demiKite(P1, P4, P3, n);
// on imprime sur la console
print("profondeur : ");
print(n);
print(" nb de formes tracées : ");
println(nbForme / 2);
// on imprime sur la partie graphique
fill(255);
String vals = String.format("%d", n);
String S1=" profondeur : "+vals;
vals=String.format("%d", nbForme/2);
S1=S1+" nb de formes tracées : "+vals;
text(S1, 10, 15);
nbForme=0; // reset du calcul
// evolution
if (sens)
{
n=n+1;
if (n>=profondeur) sens=false;
} else
{
n=n-1;
if (n<=0) sens =true;
}
// n=(n+1)%profondeur;
delay(int(attente/(log(n+2))));
}
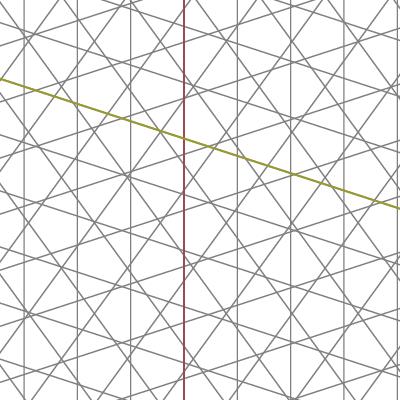
La méthode des grilles de Burjin
Cette méthode consiste en le tracé d'une série de droites, dont certaines parallèles. A l'aide des intersections de ces droites on peut retrouver un pavage de Robinson.
Approfondissements possibles
Caractérisation mathématique
Il serait interessant de parvenir à compléter la caractérisation mathématique d'un pavage à l'aide d'un langage mathématique, afin d'ajouter la caractéristique du nombre fini de types de compats.
Burjin
Il faudrait pour ce faire :
- Comprendre de manière plus approfondie la méthode des grilles de Burjin.
- Etudier cette méthode d'une manière plus mathématique et plus formelle.
- Réaliser un programme qui génère un pavage de Penrose avec cette méthode.
Bibliographie
Cours de Vincent Pilaud (polytechnique, 2006)
Cours d’Alexandre F Ritter (Oxford masterclasses in geometry, 2014)
Penrose tiles to trapdoor ciphers (Martin Gardner)
Page wikipedia pavages de Penrose (https://fr.wikipedia.org/wiki/Pavage_de_Penrose)
Wiki réalisé par CORDIER PIERRE BES Brunelle, dans le cadre de l'enseignement VISI201 à l'Université Savoie Mont Blanc.
Remerciements à Pierre HYVERNAT.