Réductions de problèmes
Transformer un problème que l’on souhaite résoudre en une ou plusieurs instances d’un autre problème que l’on sait résoudre s’appelle, en complexité algorithmique, une réduction de problème. C’est le cas du problème, utilisé dans ce projet, de couverture exacte.
Dans le cadre de ce projet, les programmes ont été écrits en python et appelés sur Ubuntu afin d’utiliser le programme Dancing Links.
Problème de couverture exacte
Définition
Le problème de couverture exacte est un problème classique en informatique et utilisé dans la résolution de problèmes logiques tels que le sudoku, le pavage par polyominos, le problème des n reines, etc.
Le problème de couverture exacte consiste à choisir des ensembles qui vont pouvoir répondre à des contraintes. Cependant, chacune de ces contraintes doivent être répondus par un unique ensemble.
Par exemple, dans le jeu du sudoku, la contrainte est que chaque case doit être remplie tel que toutes les colonnes et lignes doivent contenir exactement un chiffre de chaque type (1, 2, 3, …).
Exemples
Exemple dans les ensembles :
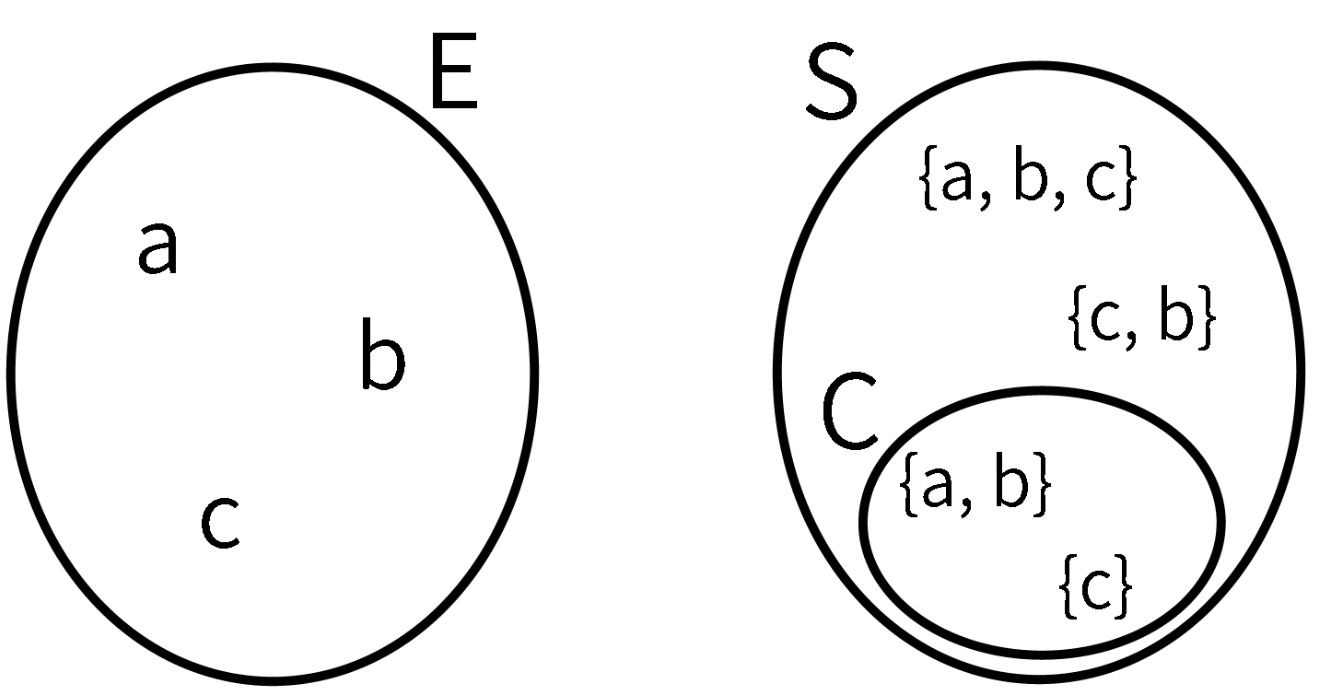
Prenons un ensemble E = {a, b, c} et un ensemble S = {{a, b}, {a, b, c}, {c, b}, {c}} de parties de E.
Une couverture exacte de E est C, un sous-ensemble de S, tel que chaque élément de E est un élément d’exactement un des ensembles de C .
Ici, C = {{a, b}, {c}}. IMAGE (légende : « Exemple de problème de couverture exacte dans les ensembles »)
Exemple dans les matrices :
Le problème de couverture exacte peut également être représenté sous forme matricielle. Les colonnes correspondent aux contraintes à respecter et les lignes aux choix possibles pour former la couverture exacte. Chaque case de la matrice contient un 1, si la contrainte est respectée, ou un 0, sinon.
Soit E = {1, 2, 3, 4} et S = {F, G, H, I, J, K}. Le problème de couverture exacte est représenté par la matrice suivante :
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| F | 0 | 1 | 1 | 0 |
| G | 1 | 0 | 1 | 0 |
| H | 0 | 0 | 0 | 1 |
| I | 0 | 1 | 1 | 1 |
| J | 1 | 1 | 0 | 1 |
| K | 1 | 0 | 0 | 0 |
Une couverture exacte de ce problème est C = {F, H, K}:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| F | 0 | 1 | 1 | 0 |
| H | 0 | 0 | 0 | 1 |
| K | 1 | 0 | 0 | 0 |
Problèmes réduits par couverture exacte
Suite de Langford
Problème
Une suite de Langford pour un entier k est une suite de 2k entiers constitué des entiers de 1 à k.
Ces entiers sont placés les uns à la suite des autres de sorte qu’un entier i soit placé à i+1 place de l’autre entier i.
Passage par une matrice
Pour résoudre les suites de Langford, on peut le réduire en instance de couverture exacte en utilisant une matrice représentant toutes les possibilités.
La matrice associée à une suite de Langford, pour un entier k, possède la structure suivante :
- Les k premières colonnes indiquent quel entier est traité ;
- Les colonnes suivantes représentent les positions (de 0 à 2*k) où placer chaque entier ;
- Chaque ligne désigne un placement possible pour deux entiers égaux.
Pour créer cette matrice, on va se baser sur la création d’une première ligne qui désigne les noms des colonnes et indique le nombre de colonnes total de la matrice.
Grâce à cette première ligne, le reste de la matrice va pouvoir être créée ligne par ligne.
Créer une ligne consiste à mettre un 1 dans la colonne correspondante à l’entier que l’on veut placer et à mettre deux 1 dans les colonnes correspondant à un emplacement possible pour la paire de cet entier. La deuxième position se déduit de la première puisqu’elle est à i+1 place de celle-ci.
Pour le bon fonctionnement du passage de la matrice, créée en python, au programme suivant, il faut d’abord la formater sous forme de string et retirer les placements symétriques de l’entier 1 (par exemple) pour ne pas avoir le double de solutions attendues (les solutions + leur symétrique).
Utilisation DLX
Afin de trouver une couverture exacte de cette matrice, nous allons utiliser le programme Dancing Links (DLX) qui prend en entrée l’ensemble des éléments d’une matrice qui sont à 1 et en sort les couvertures exactes.
Le programme python va être exécuté via Ubuntu avec les arguments nécessaires à son fonctionnement et à celui de DLX.
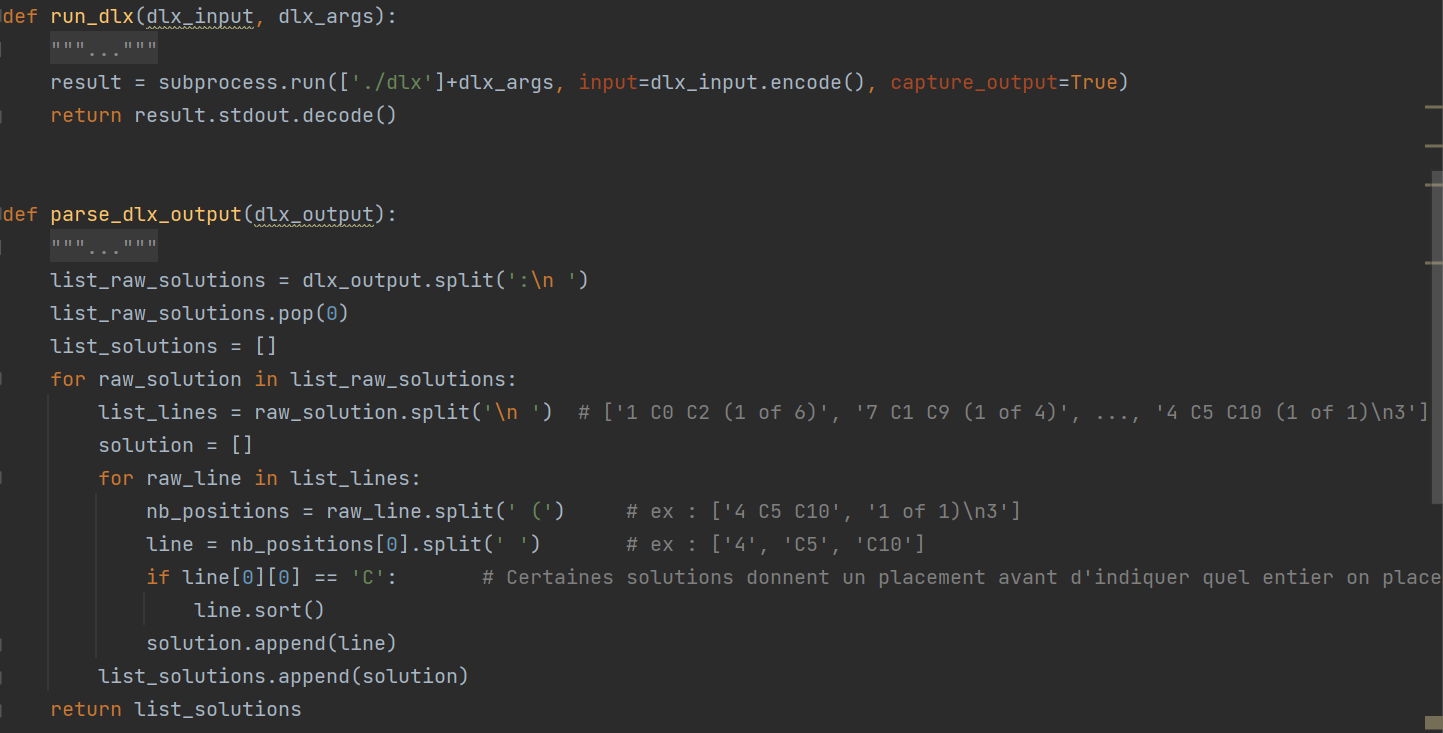
Depuis le programme python, on peut appeler DLX en lui donnant ses arguments et récupérer sa sortie.
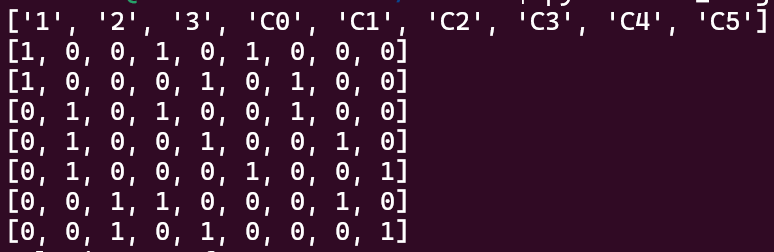
Solutions
Les solutions sont récupérées sous forme d'une longue chaîne de caractères, elles doivent donc être formatées pour les obtenir sous forme de suite de Langford.
Le problème des suites de Langford n’est pas forcément simple à résoudre, en particulier pour des grand nombre. Mais pour trouver ses solutions, on a écrit un programme python qui, algorithmiquement, n’est pas compliqué parce qu’il est réduit par couverture exacte, à l’aide de Dancing Links.
Problème de pavage avec les polyominos
Problème
Les polyominos sont des configurations formées de plusieurs carrés identiques. On retrouve les tétrominos (polyominos à quatre carrés) dans le jeu Tetris.
Un problème de pavage par les polyominos consiste à recouvrir exactement une surface prédéfinie par des polyominos.
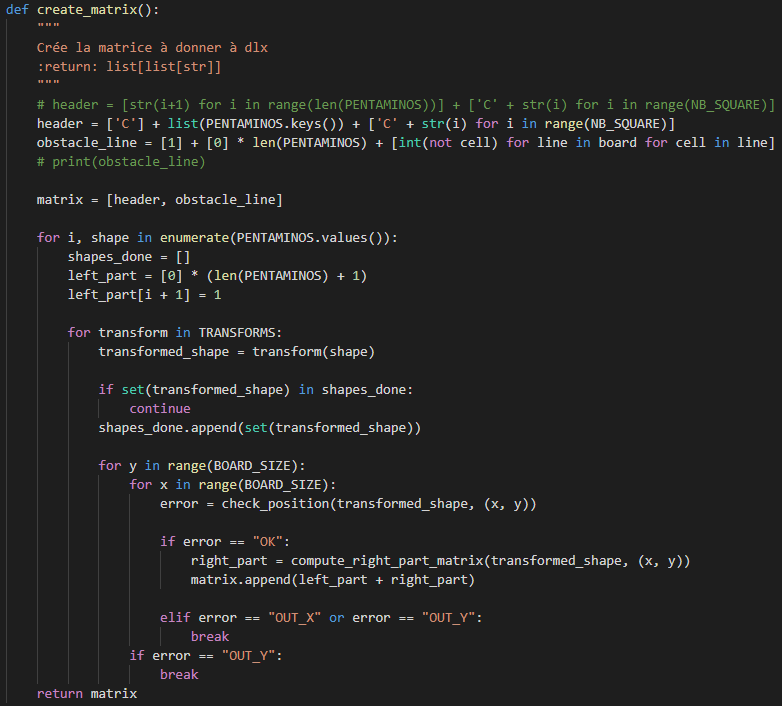
Initialisation des structures de données
Les polyominos que nous allons utiliser pour paver sont des pentaminos (polyominos à cinq carrés). Il existe douze pentaminos en tout, donc on va pouvoir définir la surface à paver comme un carré de 12*5 cases.
A cette surface on va rajouter un tétromino "obstacle" qui rajoute une contrainte au pavage. On a donc une surface totale de 64 cases, avec seulement 60 cases à paver.
Cette surface est représentée par un tableau de booléens où chaque case disponible est à True et les cases occupées par l’obstacle False.
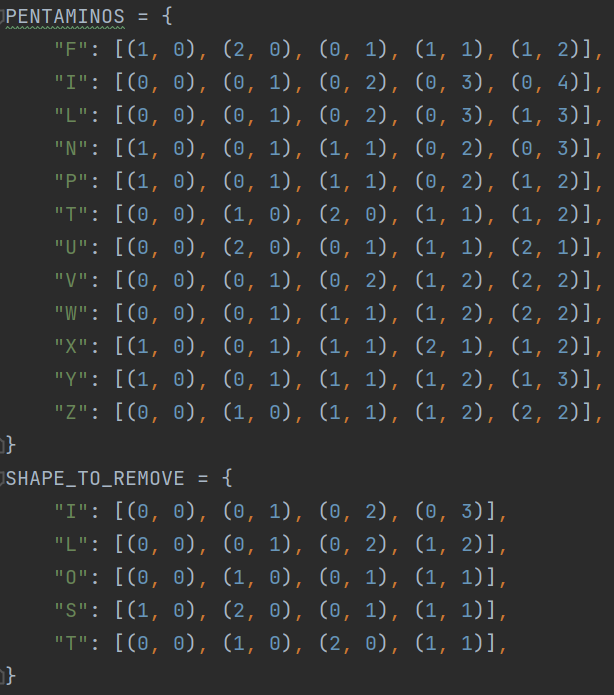
Une fois la surface définie, on va définir les pentaminos et tétrominos (pour avoir plusieurs formes possibles pour l’obstacle). Ces formes vont être stockées dans deux dictionnaires avec en clés les noms de chaque pentamino/tétromino et en valeur une liste des cases qu’elles occupent. Cette liste de cases détermine la forme prise.
Cependant placer un pentamino ne signifie pas placer uniquement sa forme décrite dans le dictionnaire, mais également placer ses rotations et symétriques (si nécessaire). Ainsi un pentamino aura le même nom s’il s’agit d’un symétrique ou d’une rotation de la forme originale.
Pour les créer, des fonctions de rotation et de symétrie sont utilisées.
Passage par une matrice
Pour réduire ce problème de pavage par le problème de couverture exacte, il faut, comme pour une suite de Langford, passer le problème sous la forme d’une matrice.
La matrice associée au pavage par pentaminos possède la structure suivante :
- Colonnes :
- La première désigne le nom du tétromino obstacle ;
- Les 12 suivantes désignent les noms des 12 pentaminos ;
- Les 64 suivantes désignent les cases où on peut placer un pentamino.
- Lignes :
- La première désigne l’emplacement fixe de l’obstacle ;
- Les suivantes représentent chaque possibilité de placement de chaque pentaminos sur la surface à paver.
Pour placer un pentamino, on va parcourir la surface totale de ligne en ligne en vérifiant si toutes les cases composant le pentamino sont comprises dans la surface à paver. Donc on teste si le pentamino ne dépasse pas de la surface totale et ne possède pas des cases en commun avec l’obstacle.
Si un placement du pentamino respecte ces deux contraintes, on le met dans la matrice en indiquant le pentamino placé et chaque case de la surface totale qu’il occupe par des 1.
Cette opération est répétée pour chaque pentamino.
Cette matrice doit de nouveau être formatée pour la donner à DLX.
L’appel de DLX et son fonctionnement reste le même.
Solutions
Le pavage par polyominos étant un problème visuel, les solutions vont être affichées dans des images avec chaque pentamino de couleurs différentes. La taille d’une image est créée grâce à la taille de la surface totale. Cette surface est un carré de 8*8 cases qui possèdent une taille en pixel, ici les cases sont des carrés de 50*50 pixels.
Une solution est sous forme de liste de pentamino avec le nom du pentamino placé et les cases qu’il occupe.
Après avoir créée une image et d’y avoir dessiner une grille (pour mieux différencier les cases), on dessine chaque pentamino un à un, case par case. Si la ligne correspond à la position de l’obstacle, il est dessiné d’une couleur noir pour bien le différencier.
Machines de Turing
Machine déterministe à un ruban
Une machine de Turing est un modèle abstrait qui reflète ce qu’un appareil de calcul, comme un ordinateur, est capable de faire. Elle est composée d’un ruban, souvent infini à gauche et à droite, qui représente une mémoire infinie.
Sur le ruban d’une machine de Turing, nous allons trouver une tête, pointant une des cases, qui va lire et/ou écrire sur le ruban et se déplacer.
Chaque machine est définie par :
- Un alphabet fini Σ : ensemble des symboles utilisés par la machine ;
- Un ensemble fini des états des têtes : état initial, d’acceptation, de rejet, etc. ;
- Une table de transition : décrit – en fonction de l’état de la tête de lecture et du symbole lu par celle-ci – ce qui doit être doit écrit, dans quel état elle doit passer et son sens de déplacement.
Exemples
Exemple d'une machine à un ruban :
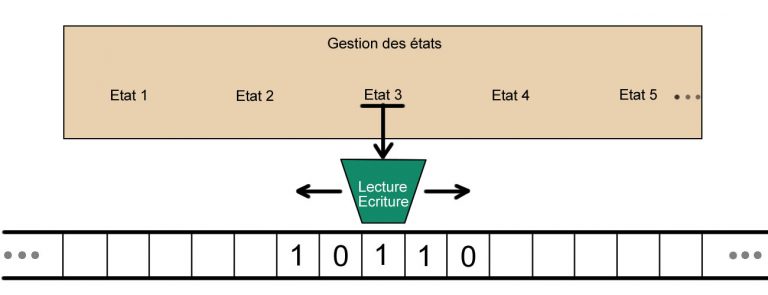
Imaginons une machine de Turing à un ruban infini, une tête et travaillant sur l’alphabet Σ = {1, 0}. Un ruban est majoritairement composé de 0 et ne possède des 1 que sur une portion finie de ruban. Cette machine a pour but de remplacer le premier 0 rencontré en 1.
A l’état initial, la tête est placée sur une case 1. Elle va lire la case et passer dans un nouvel état : elle va se déplacer d’un cran vers la droite. La tête va repasser dans l’état précédent et lire la nouvelle case.
Si elle lit un 1, elle va de nouveau prendre l’état de déplacement vers la droite.
Si la tête lit un 0, elle va passer dans un nouvel état, celui d’écriture, et va écrire un 1 à la place du 0.
La machine a remplacé le premier 0 rencontré par un 1, elle passe dans un dernier état : l’état d’acceptation.
Exemple d'une machine à deux rubans : Fichier:MachineTuring.pdf
Machine de Turing non déterministe
La différence avec une machine déterministe est qu'une machine de Turing non déterministe possède plusieurs transitions activables suite au passage d’un état. Ces machines peuvent "inventer" des solutions à un problème et vérifier qu’elles sont bien solutions.
Classes de complexité
Le modèle des machines de Turing permet de définir les classes de complexité algorithmique. Le temps mis par une machine M sur une entrée x est le nombre d’étapes du calcul de M(x) pour arriver un état final.
Classe P
Un problème est dans la classe P s’il est décidé par une machine de Turing déterministe en temps polynomial. Les problèmes de la classe P sont considérés comme des problèmes "faciles à résoudre", soit qui sont rapide à résoudre.
Classe NP
Un problème de classe NP (non déterministe polynomial) est décidé par une machine de Turing non déterministe en temps polynomial. Les problèmes de cette classe sont considérés comme les problèmes "faciles à vérifier".
NP-complet
Un problème NP-complet est un problème de classe NP auquel tous les autres problèmes de classe NP peuvent être ramené via une réduction polynomiale.
Le problème de couverture exacte est un problème NP-complet, c’est notamment pour cela qu’il est utilisé pour faire de la réduction de problèmes.
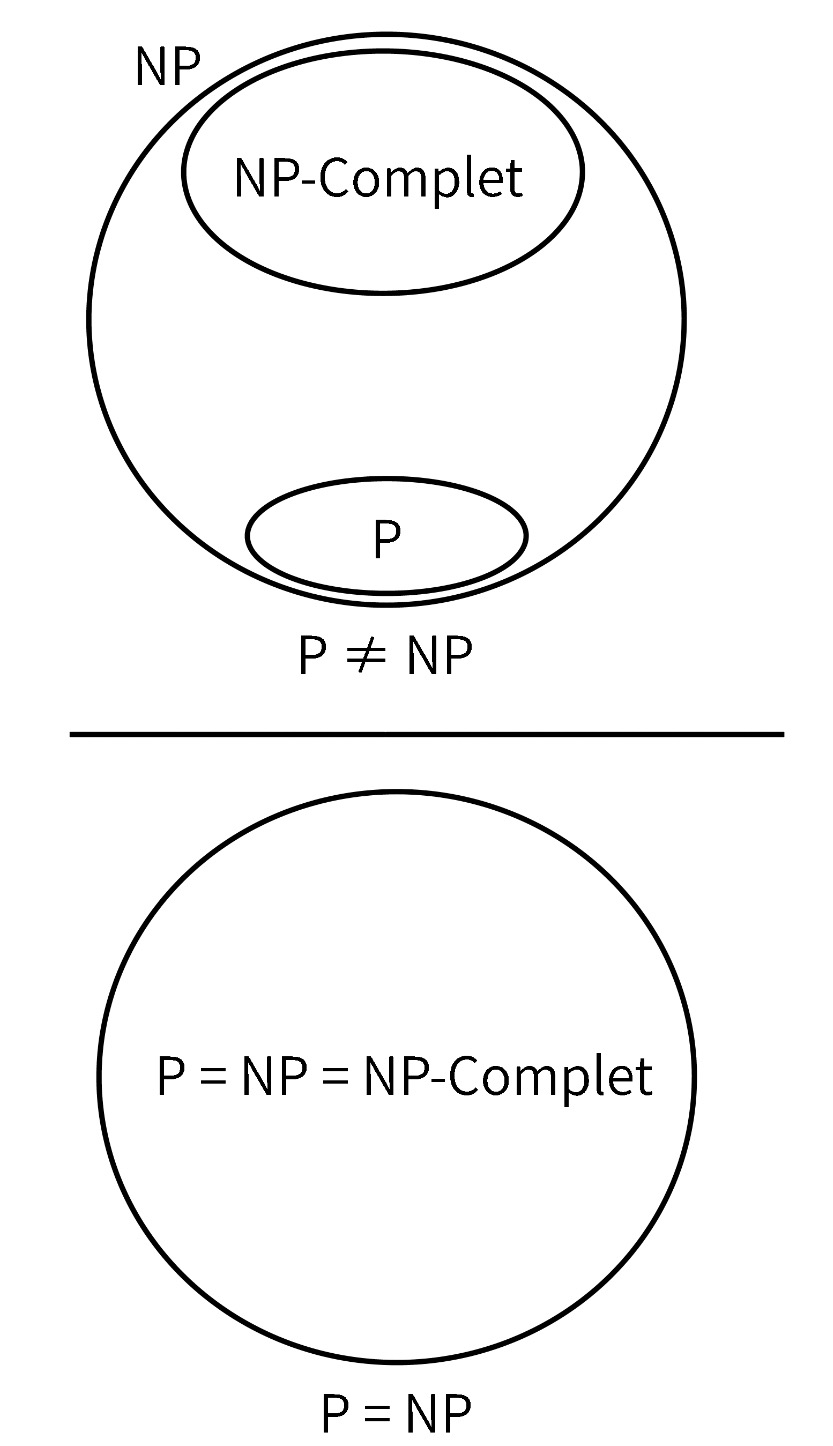
Problème P≟NP
Aujourd’hui on sait qu’un problème facile à résoudre est considéré facile à vérifier, soit P⊆NP.
Résoudre si P=NP revient à se demander si trouver une solution est aussi simple que de vérifier une solution. Par exemple, est-il aussi facile de remplir une grille de Sudoku que de vérifier qu’un remplissage est bien une solution.
Une manière proposée pour résoudre P=NP est de montrer qu’un problème NP-complet est également de classe P. Comme tous problèmes de classe NP peuvent se ramener par réduction à un problème NP-complet, alors tous ces problèmes se réduiraient à un problème de classe P.