Surfaces polygonales et surfaces de subdivision
Élève : Vetea STOLL
Tuteur : Jacques Olivier Lachaud
Définitions
Surface
Ensembles de points sur lequel il est localement possible de se repérer à l'aide de deux coordonnées réelles.
Surface polygonale
Donnée d'un ensemble de polygône dans l'espace s'intersectant deux à deux suivant des arêtes
Structure de données demie arêtes ailées
Description
Dans cette structure de données les arêtes (ex point A et B) sont décomposée en 2 demie arêtes (A vers B et B vers A) sont définies implicitement par un indice.
Chaque demie arête a une demie arête suivante (next) une demie arête opposée (opp) un point vers lequel la demie arête pointe (to_vertex) et l'indice de la face à laquelle la demie arête est associée (face), si il n'y a pas de face on mettra -1 par convention.
Pour accéder à ces paramètres on définie des listes de longueur n avec n nombre de demie arêtes pour chaque paramètre.
Les faces ont une demie arête associée de façon arbitraire (w_face) également pour les points (w_vertex).
On fera également des listes pour ces paramètres de longueur n avec n nombre de face et nombre de points.
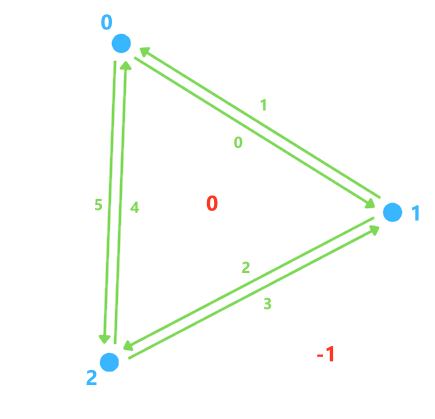
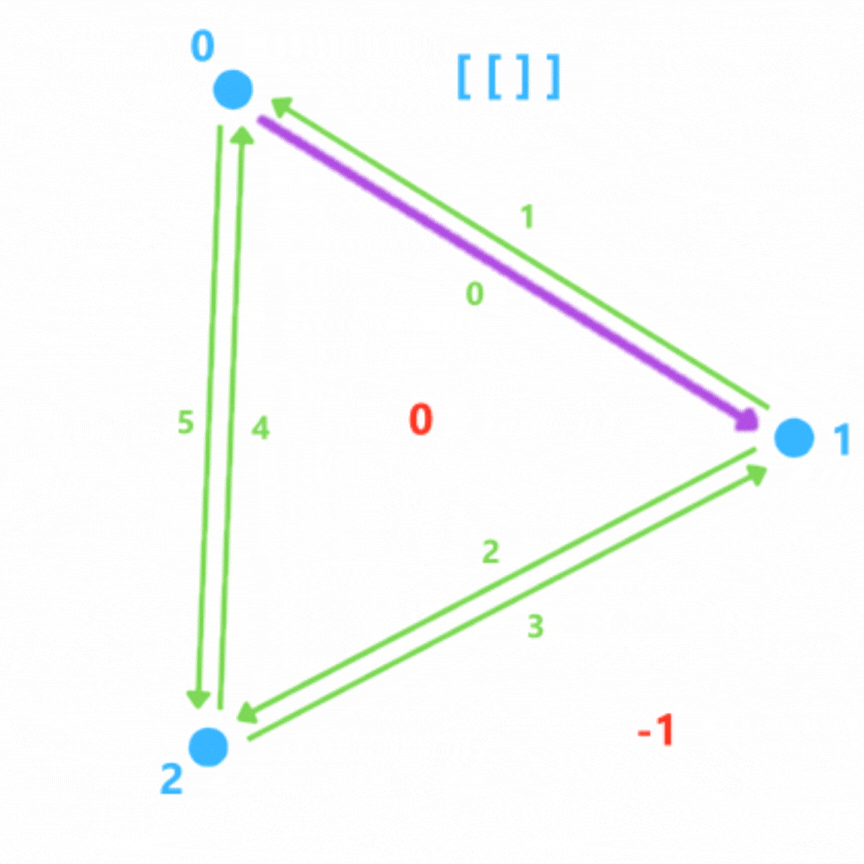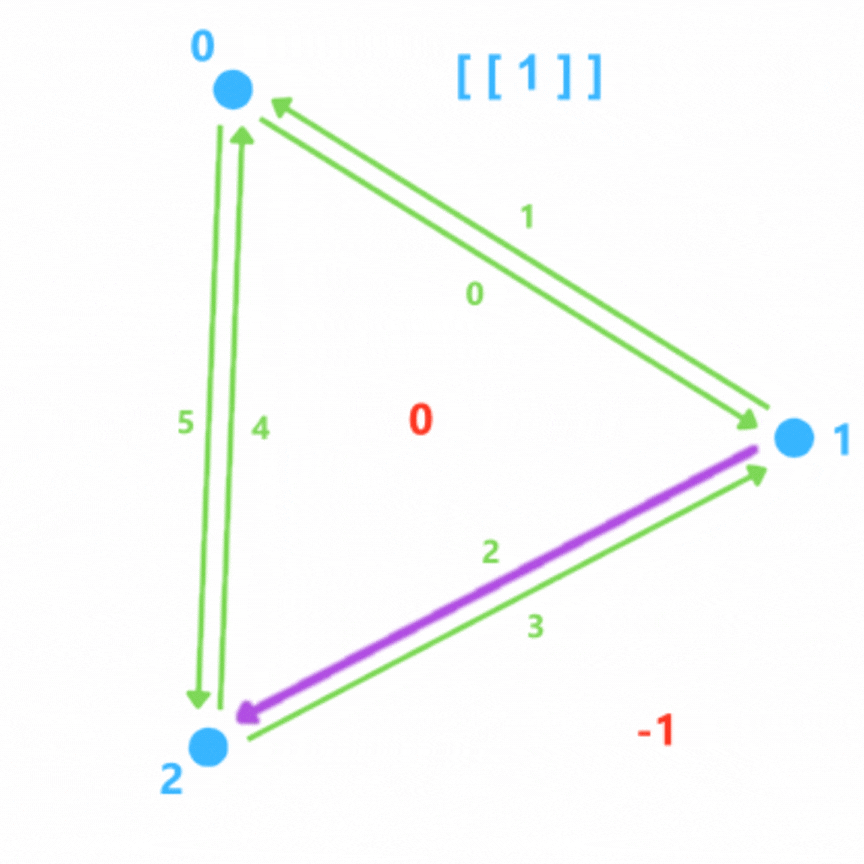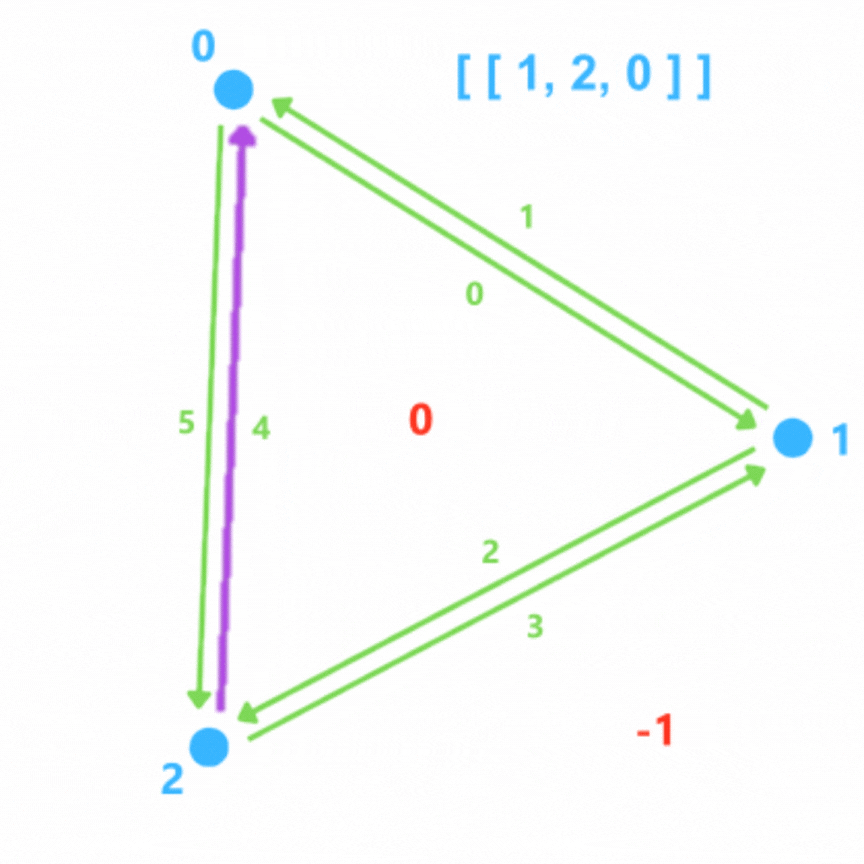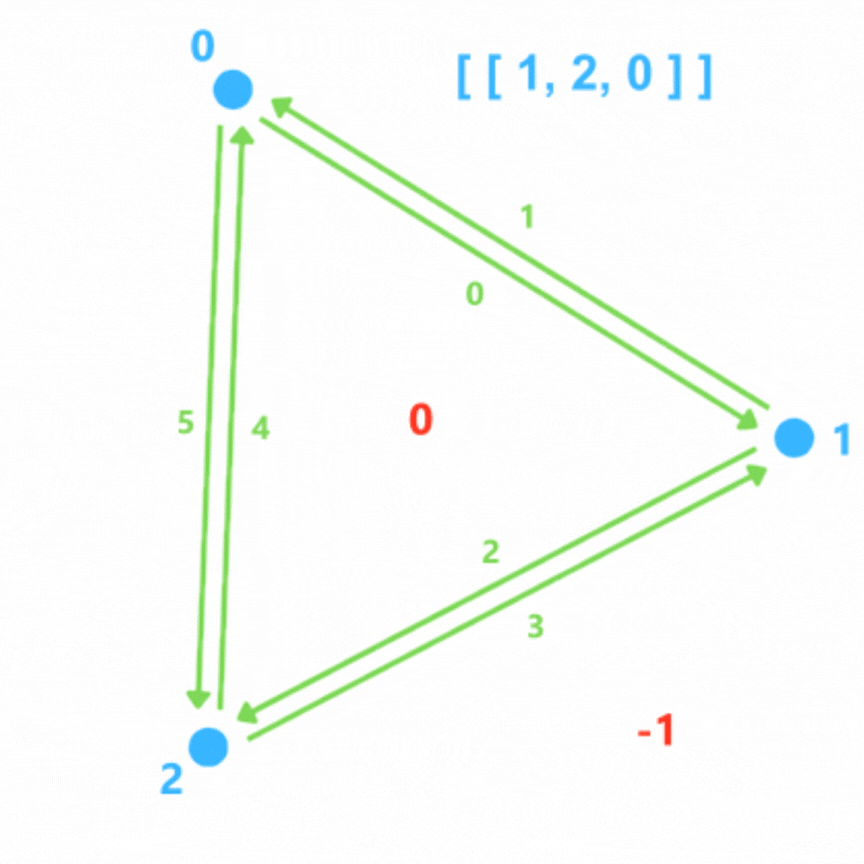
La structure de donnée d'un triangle ressemblera à ça :
next : [2,5,4,1,0,3]
opp : [1,0,3,2,5,4]
to_vertex : [1,0,2,1,0,2]
face : [0,-1,0,-1,0,-1]
w_face : [0]
w_vertex : [1,3,5]
On utilise cette structure de données car elle est plus facile à manipuler pour faire la subdivision par la suite.
Conversion
La structure de données qu'on a est définie par une liste de faces, chaque face étant une liste contenant les index des points associés.
Notre triangle ressemblerait alors à ça :
faces = [ [0,1,2] ]
On parcourt la liste des faces et on parcourt chaque face. On a donc des arêtes définies par pointA = faces[ i ] [ j ] et pointB = faces[ i ] [ (j+1) % len(faces[ i ]) ].
On peut alors définir une demie arête (pointA -> pointB) ainsi que son opposée (pointB -> pointA) en faisant attention attention qu'elle n'aie pas déjà été définie.
Pour définir des indices aux demies arêtes il suffit de garder en mémoire le nombre d'itérations qui ont eu lieu, qu'on va appeler n. Chaque demie arête aura l'indice 2n et chaque demie arête opposée aura l'indice 2n+1
Les listes sont alors un jeu d'enfant à remplir, excepté next, en particulier quand on définie les demies arêtes opposées car on ne sait pas à l'avance quel sera la demie arête suivante. On les définie alors par -1 temporairement.
Quand l'algorithme continue, si quand on veut définir une demie arête on se rend compte qu'elle a déjà été créée, on met à jour ses listes next et face. Mais il reste alors les demies arêtes du bord.
Après avoir executé cette première partie de la conversion, on s'occupe donc des next pour les demies arêtes opposées.
On commence par parcourir la liste des demies arêtes au bord (celles pour lesquelles la face associée est -1) et pour chaque demie arête, on prend l'opposée et tant que la demie arête n'est pas au bord, on prend l'opposée de la demie arête précédente (Pour trouver la demie arête précédente il suffit de prendre la demie arête suivante jusqu'a ce qu'on retombe sur celle que l'on avait au départ, on aura donc la demie arête précédente en mémoire).
Cette demie arête est donc la suivante de celle que l'on avait au départ.
Déconversion
La déconversion est un peu plus simple. On commence par parcourir w_face, et on rajoute le to_vertex de la demie arête dans une liste tant que la demie arête suivante n'est pas celle que l'on avait au départ.
Algorithmes de subdivision de surface
Catmull-Clark
Pour mon implémentation de la subdivision de surface Catmull–Clark, je l'ai décomposée en 2 parties.
La première partie s'occupe de subdiviser les arêtes tandis que la deuxième s'occupe de subdiviser les faces.
Partie 1 - subdivision des demies arêtes
Dans la première partie, on parcourt les demies arêtes d'indice pair car on va s'en occuper par paires, comme pendant la conversion.
On aura donc besoin de créer 1 point et 2 demies arêtes par paires de demies arêtes.
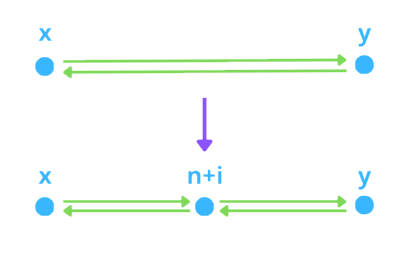 ici n = nombre de points qu'on avait à la base et i = l'indice du nouveau point.
ici n = nombre de points qu'on avait à la base et i = l'indice du nouveau point.
 ici n = nombre de demies arêtes qu'on avait à la base et i pair
ici n = nombre de demies arêtes qu'on avait à la base et i pair
On peut voir que la demie arête opposée d'une demie arête x est égal à x+1 si x pair et x-1 si x impair, grâce à la méthode de conversion, et on va garder cette propriété tout le long de la subdivision même si elle n'est pas obligatoire.
Lors de cette première partie de la subdivision on double les demies arêtes et on ajoute 1 point par paire de demies arêtes.
Partie 2 - subdivision des faces
Pour la subdivision des faces on parcourt toutes les faces avec w_face et on créé 1 point et autant de faces qu'il y avait de points sur la face avant toute subdivision.
On définit n[f] : nombre de points de la face avant la subdivision.
Lors de cette deuxième partie de la subdivision pour chaque face on ajoute 2 * n[f] demies arêtes, on ajoute 1 point par face et on ajoute n[f]-1 faces.
On définie P : nombre de points, A : nombre de demies arêtes, F : nombre de faces et N : somme de n[f] de chaque face.
Donc après les 2 parties de la subdivision,
P = P + A/2 + F
A = 2A + 2N
F = N
Définitions des coordonnées des points
Les points de faces ont pour coordonnées la moyenne de tous les points originaux de la face.
Les points d'arêtes ont pour coordonnées la moyenne des 2 points de l'arête et des 2 points de faces des 2 faces associées à l'arête.
Pour les coordonnées des points originaux P, on commence par définir F la moyenne des n points de faces touchant P, R la moyenne du milieu des n arêtes touchants P (le milieu d'une arête étant la moyenne des 2 points de l'arête). Les nouvelles coordonnées de P sont alors .
Exemples
Voici l'exemple d'un modèle d'un lemming fait main sur blender avec 0, 1, 2 et 3 subdivisions Catmull-Clark :
Un cube avec 0, 1, 2 et 3 subdivisions Catmull-Clark :
Autres aglorithmes
Subdivision √3
La subdivision √3 est utilisée sur des surfaces triangulées, c'est à dire une surface composée uniquement de faces triangles.
On commence par définir un point central sur chaque face, qu'on relie à tous les autres points du triangle.
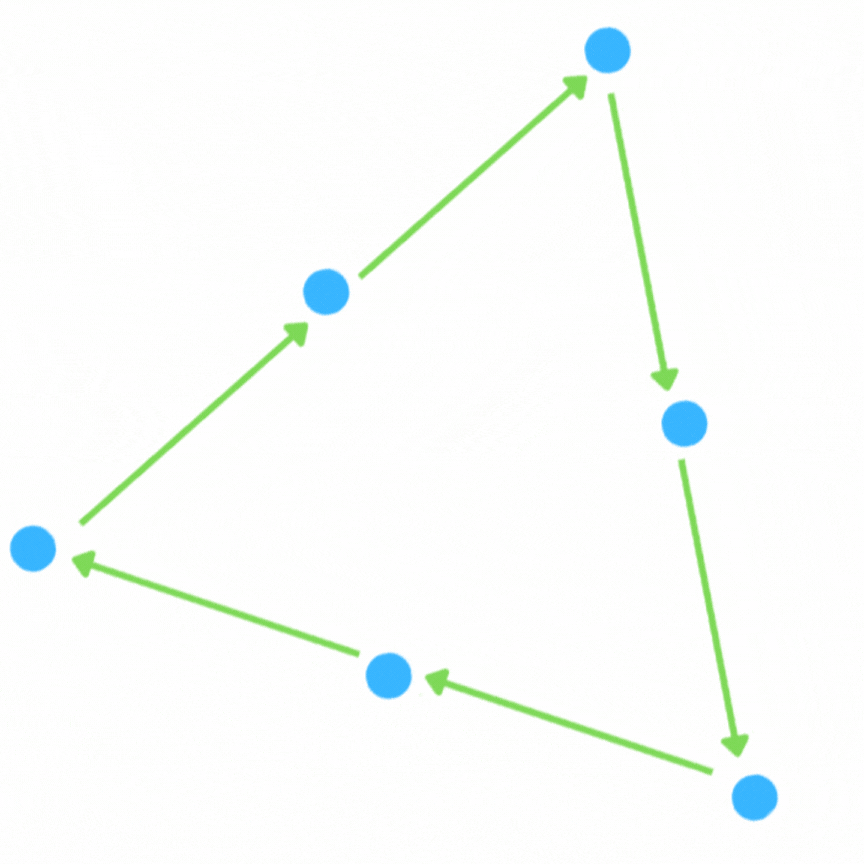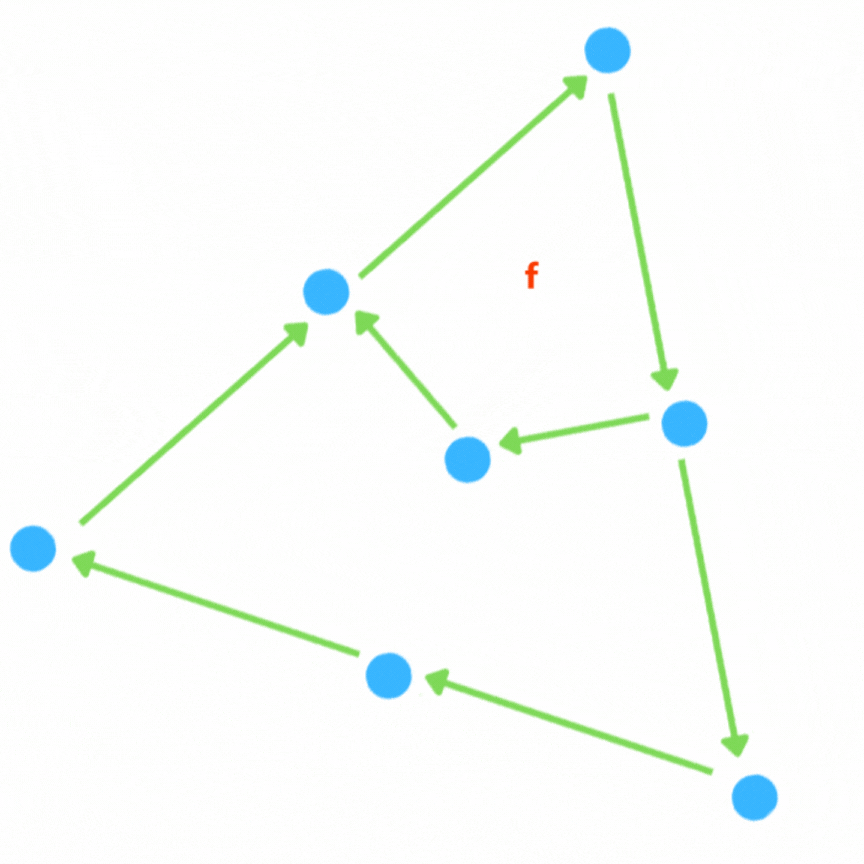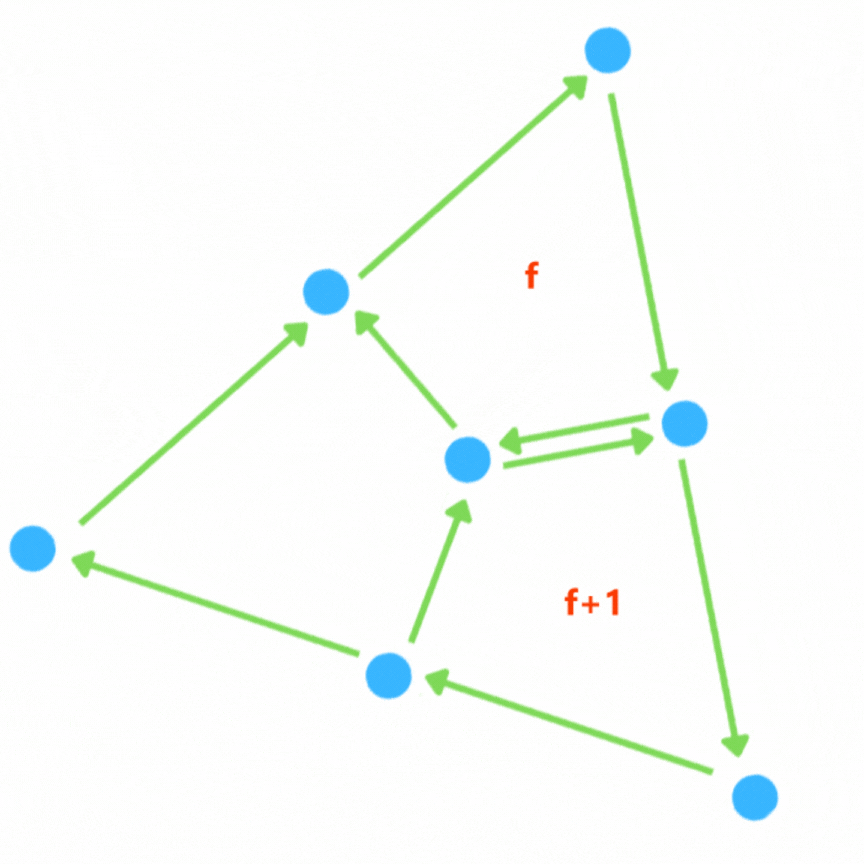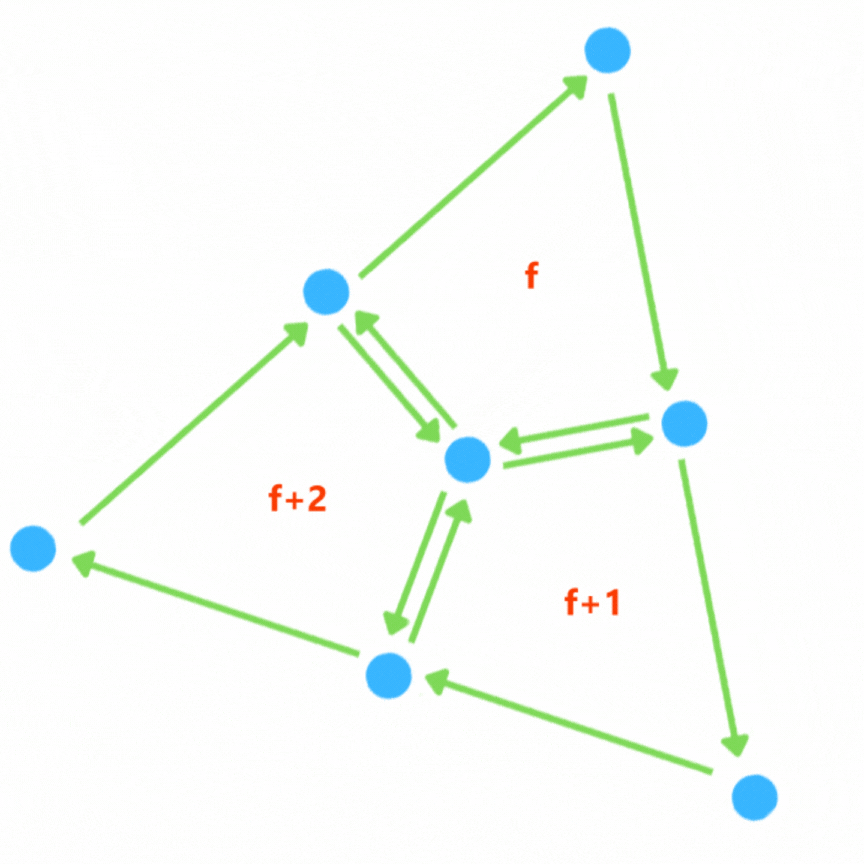
On supprime ensuite les arêtes qu'il y avait à la base si elles ne sont pas au bord et on relie les nouveaux points avec leurs voisins (les nouveaux points des faces adjacentes) par une arête.
Cette subdivision multiplie les faces par 3, créée 1 points par face et créée 3 arêtes par face.
Donc si f est le nombre de face qu'il y avait à la base on a :
nombre de faces += 2f
nombre de points += f
nombre d'arêtes += 3f