Réalisé par : Ambroise Decouttere, étudiant en CMI-INFO

Introduction

Le traitement d’image est une discipline de l’informatique et des mathématiques appliquées qui étudie les images numériques et leurs transformations, dans le but d’améliorer leur qualité ou d’en extraire de l’information.

Le traitement d’image est quelque chose d’énormément utilisé que ce soit par des particuliers ou des professionnels. Il est aussi bien utilisé dans l’imagerie médicale que dans la prise de photo avec un smartphone.

Les couleurs

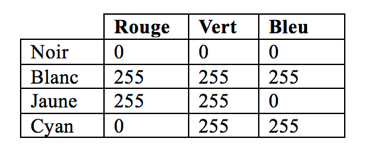
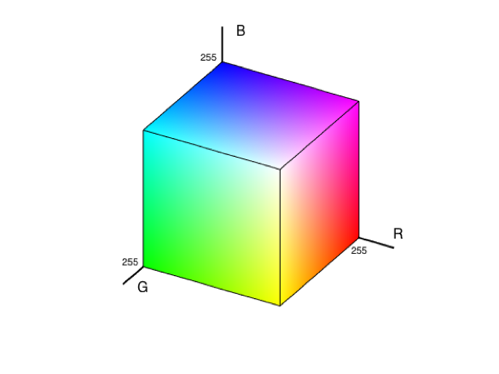
Pour chaque pixel est associé un triplet de valeurs (rouge, vert, bleu). On appelle ce codage le RGB (Red Green Blue). Le point fort de cette méthode de codage est sa simplicité puisqu’il ne nécessite aucun calcul de la part de l’ordinateur. Chaque couleur est codé sur 1 octet (256 bits), et quand les 3 couleurs sont placées à côté, on ne distingue pas chaque couleur mais seulement la couleur du pixel par synthèse additive. Cependant, le codage en RGB a quelques limites, par exemple il ne peut pas représenter toutes les couleurs perceptibles par l’œil même s’il en représente une très grande partie.

Voici à quoi ressemble le codage de différentes couleurs en RGB :

Représentation de l'espace RGB :

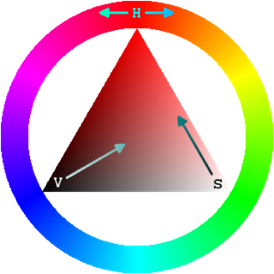
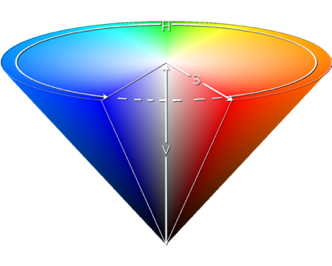
Il existe d’autres manières de coder les couleurs : HSV par exemple. HSV correspond à Hue Saturation Value. Celui-ci aussi est codé sur 3 valeurs :

• La teinte (Hue) est codée suivant l’angle correspondant sur le cercle des couleurs : - 0° ou 360° rouge ; - 60° jaune ; - 120° vert ; - 180° cyan ; - 240° bleu ; - 300° magenta.

• La saturation est l’intensité de la couleur : - elle varie entre 0 et 100 % ; - elle est parfois appelée « pureté » ; - plus la saturation d’une couleur est faible, plus l’image sera grisée et apparaitra fade. Donc par exemple pour avoir un rouge entièrement saturé il faudrait que la Saturation soit égale à 100%.

• La valeur (Value) est la brillance de la couleur : - elle varie entre 0 et 100 % ; - plus la valeur d’une couleur est faible, plus la couleur est sombre : une valeur de 0 correspond au noir.

Donc le format HSV est basé sur la perception des couleurs et utilise trois composantes définies par une approche psychologique et perceptuelle de la couleur. Passage RGB vers HSV :

Pour visualiser l’espace HSV, on peut se servir de c’est deux formes qui représente bien ce format et permet de mieux comprendre à quoi correspond chaque valeur H, S et V :

Une image en noir et blanc sera par contre codé par seulement 1 bit qui prendra la valeur 0 (pour du noir) ou 1 (pour du blanc). Cependant, cette image n’aura aucunes teintes séparant le noir du blanc.

Ainsi, on arrive aux images en niveaux de gris qui seront comme une image en noir et blanc mais avec au total 256 teintes différentes (donc codée avec 1 octet par pixel). Pour coder une image en niveaux de gris, il faut donc choisir une valeur comprise entre 0 et 255 qui définira l’intensité du gris sachant qu’un octet prenant la valeur 0 représente du noir et 255 représente du blanc.

Les images

Il existe 2 représentations d’image possible : matricielle et vectorielle.

L’image matricielle est composée d’une matrice de points à plusieurs dimensions, où chaque dimension représente une dimension spatiale (dans le cas d’une image en 2D on aura la hauteur et la largeur). Ce type d’image s’adapte bien à l’affichage sur écran car ceux-là fonctionne également d’une manière matricielle (disposition des pixels), mais moins à l’impression car les écrans possèdent une résolution de 72 à 96 ppp (« points par pouces ») alors que les imprimantes ont une résolution d’au moins 600 ppp : donc la page imprimée pourra comporter des pixels carrés visibles ou sera floue si sa résolution n’est pas suffisante. Les images matricielles sont beaucoup plus utilisé notamment car les appareils photos enregistre les photos en format matricielle.

Le principe d’une image vectorielle est de représenter les données de l’image par des formules géométriques qui vont pouvoir être décrites d’un point de vue mathématiques. On stock donc la succession d’opérations conduisant au tracé. L’avantage de ce type d’image est qu’elle peut être agrandie à l’infini sans perdre la qualité de l’image initiale. Cependant, la plupart des écrans d’ordinateur actuel ne peuvent pas lire les images vectorielles, on doit donc la convertir en image matricielle avant de l’afficher.

La définition d’une image est définie par le nombre de point qui la représente, par exemple si une image est composée de 900 pixels en hauteur (sur l’axe vertical) et 1250 pixels en largeur (sur l’axe horizontal), alors on dira de l’image qu’elle a une définition de 900 x 1250.

La résolution d’une image fonctionne de la même manière que la résolution d’un écran : elle correspond aux ppp et donc pour une image de même dimension, plus la résolution de l’image est élevée, plus le nombre de pixels qui composent l’image est important. Le nombre de pixels est proportionnel au carré de la résolution donc augmenter la résolution d’une image va également augmenter l’espace nécessaire pour la stocker.

Exemple de différentes résolutions d’une image de même dimension :

Familles de traitement d'image

Restauration

Technique d'imagerie numérique permettant de rendre son aspect d'origine à une image, souvent utilisé dans le but d'améliorer l'apparence physique d'une image. Une restauration peut être faite avec une intervention humaine par exemple dans les restaurations de document ancien, ou sans aucune intervention sur les documents moins important ou qui n’en ont pas besoin. Une restauration d'image peut améliorer la luminosité et le contraste ou recalibrer le profil colorimétrique.

Égalisation d'histogramme

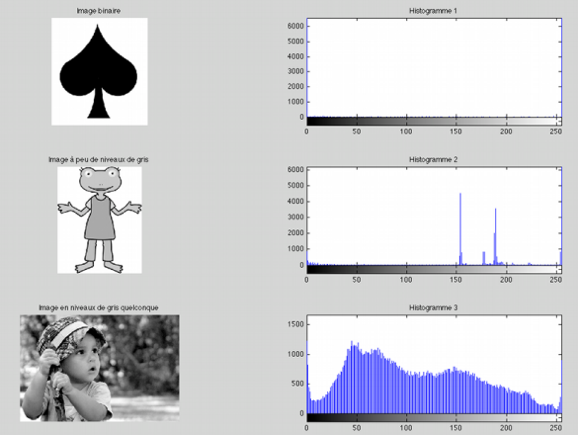
Un histogramme est une fonction décrivant les niveaux de gris d’une image. Il permet de connaitre la distribution statistique des niveaux de gris mais ne donne aucune information sur la disposition spatiale des différents niveaux de gris, donc une image ayant seulement subit une rotation aura le même histogramme que l’image de départ. Exemple d’histogramme :

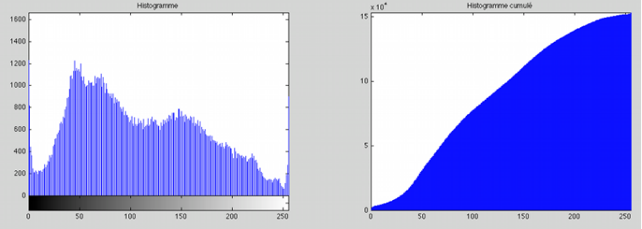
Pour trouver l’histogramme d’une image il suffit de compter le nombre de pixels ayant la même intensité de gris puis de mettre les résultats dans un graphique. On peut ensuite faire l’histogramme cumulé de cette image en refaisant un nouveau graphique ou chaque valeurs est additionner avec la précédente. La représentation graphique de l'histogramme cumulé correspond à :

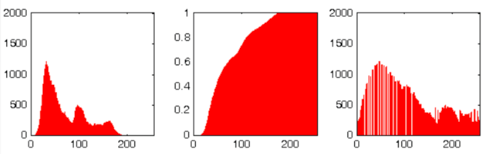
Il suffit ensuite de modifier les valeurs de l’histogramme cumulé pour obtenir une droite et non une courbe, ainsi on « étale » l’histogramme pour que les valeurs soient mieux réparties. Ensuite tous les pixels sont modifiés en fonction de l’histogramme cumulé modifié pour obtenir une image avec des couleurs plus « agréable » et avoir un meilleur rendu. Une égalisation d’histogramme va donc modifier l’histogramme de l’image :

Avec en premier l’histogramme de base de l’image, ensuite l’histogramme cumulé de l’image puis a la fin l’histogramme après égalisation.

Élimination du flou de déplacement

Le flou de déplacement fait partie des « bruits » qui peuvent venir réduire la qualité de l'image de différentes manières. Ici, il s'agit soit du flou cinétique (ou flou de mouvement) qui est due au mouvement rapide du sujet photographié, soit ou flou de bougé qui lui est due au mouvement de l'appareil photo pendant la prise de vue. Le but de ce traitement est donc d'éliminer toute les imperfections dues au mouvement du photographe ou du mouvement du sujet photographié.

Segmentation

Le but de la segmentation est de rassembler des pixels entre eux en fonction de critères prédéfinis. Les pixels sont donc regroupés en régions qui constituent une partition de l'image (si le nombre de classes est égal à 2 on parle de binarisation). Souvent utilisé pour séparer les objets du fond. La segmentation est une partie importante du traitement d’image car contrairement à l’Homme qui sait différencier les objets qui constitue une image, la machine ne fait pas naturellement cette différentiation. Il y a différents types de segmentation : - La segmentation fondée sur les régions. (1) - La segmentation fondée sur les contours. (2) - La segmentation fondée sur la classification ou le seuillage des pixels en fonction de leurs intensités. (3) - La segmentation fondée sur la coopération entre les trois premières segmentations. (4)

1. Pour faire une segmentation basée sur les régions on peut utiliser deux techniques différentes, soit on part d’une première partie de l’image que l’on modifie en divisant ou regroupant des régions (décomposition ou fusion), soit on commence avec quelques régions que l’on agrandie an y ajoutant des pixels jusqu’à ce que toute l’image soit couverte (croissance de régions). Il y a également des méthodes fondées sur la modélisation statistique conjointe de la régularité des régions et des niveaux de gris de chaque région. Les algorithmes utilisant la décomposition/fusion se base sur les caractéristiques propres de chaque région (surface, intensité lumineuse, colorimétrie, texture, etc.). On va chercher des couples de régions candidates à une fusion et on va noter l’impact que cette fusion aura sur l’apparence générale de l’image. On va ensuite pouvoir fusionner les couples de régions ayant les meilleures notes. On refait ces opérations jusqu’à ce que les caractéristiques de l’image remplissent une condition prédéfinie : nombres de régions, luminosité, contraste, …, ou alors jusqu’à ce que les meilleures notes obtenues n’atteignent plus un certain seuil (on parle alors d’algorithme avec minimisation de fonctionnelle). Les algorithmes de croissance partent d’un premier ensemble de régions, pouvant être calculées automatiquement (par exemple les minima de l’image), ou fournies par un utilisateur de manière interactive. Les régions vont ensuite grandir par ajout des pixels les plus similaires par au critère donné (par exemple la différence entre le niveau de gris moyen de la région et celui du pixel donné). Les algorithmes fondés sur une modélisation statistique conjointe des régions et des niveaux de gris prennent en compte à la fois la vraisemblance de l’appartenance du pixel à une région en fonction de son niveau de gris et les régions auxquelles appartiennent les pixels voisins. Cette fonction permet donc de faire un compromis entre la régularité des régions segmentées et la fidélité de l’image initiale.

2. Les algorithmes de segmentation fondés sur le contour se servent des différences de couleurs (ou niveaux de gris) qui forment la transition entre deux objets d’une image. Ces algorithmes doivent résoudre deux problématiques : Caractériser la frontière entre les régions et réussir à fermer les contours. Il existe plusieurs types d’approches permettant de détecter les contours dans une image, il y a l’approche gradient et l’approche Laplacien. http://alpageproject.free.fr/doc/RAPPORT_TER_final_1.pdf (page 13 à 22) http://webia.lip6.fr/~thomen/Teaching/BIMA/cours/contours.pdf

3. La segmentation fondée sur la classification ou le seuillage des pixels en fonction de leurs intensités permet de créer différentes régions en fonction de l’intensité de la couleur de chaque pixel. Pour cette technique, il serait donc plus pratique de s’assurer que l’image est codée dans l’espace HSV, puisque la Saturation correspond à l’intensité de la couleur. Donc on aura qu’à prendre chaque pixel et les regrouper en fonction de leur Saturation. Cependant on pourrait également utiliser cette segmentation mais sans se baser sur l’intensité, dans ce cas-là il suffirait de s’adapter à ce qui est recherché sachant que l’on va comparer la valeur choisie de chaque pixel avec une moyenne calculé sur toute l’image.

4. Enfin, on pourrait également mélanger ces trois algorithmes pour obtenir une segmentation la plus optimale possible en prenant les parties qui nous intéressent pour la segmentation recherchée.

Famille de technique de traitement d'image

Dans les types de filtrage suivant (filtrage spatial et filtrage fréquentiel), on a besoin d’un outil appelé la Transformée de Fourier. Commençons donc par voir comment fonctionne la transformée de Fourier : Nous utiliserons la Transformée de Fourier Rapide (FFT) qui correspond à la Transformée de Fourier mais avec un calcul bien plus rapide à réaliser que la formule initiale. Celle-ci permet de passer d’une représentation spatiale à une représentation de l’image dans le domaine fréquentiel.

L’utilité de cet outil est qu’il va nous permettre de voir l’image d’une autre manière que sa représentation spatiale. Voici ce que donne la FFT de différentes images :

Filtrage spatial

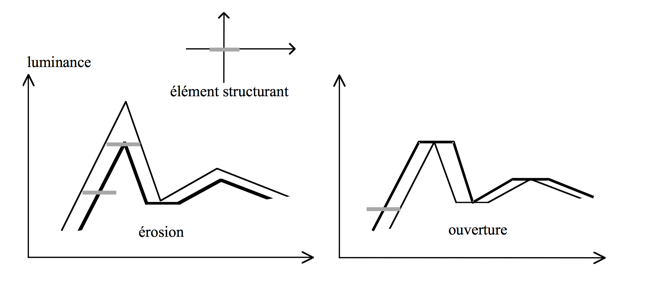
Le filtrage spatial est une méthode permettant de sélectionner des composantes spatial d’une image. C’est-à-dire qu’on va ici s’intéresser à la forme des objets qui composent une image. Cette technique permet donc de modifier une image en fonction de ce qu’elle représente plutôt qu’en fonction de ses couleurs. Exemple de filtrage morphologique spatial : érosion / dilatation / ouverture / fermeture … Voyons comment ces algorithmes fonctionnent dans le cas d’une image en noir et blanc (1 bit) :

On va d’abord devoir choisir un élément structurant, c’est-à-dire une configuration élémentaire de pixels à rechercher dans l’image (un des pixels sera l’origine de l’élément structurant) (on appellera B l’élément structurant et X l’image).

- L’érosion : Pour chaque position de B sur l’image X, si tous les pixels de B font partie de X, alors l’origine de B appartient à l’image générée. Donc l’érosion d’une image en noir et blanc va en général réduire la présence de pixel noir sur l’image. Au contraire, si on fait une érosion sur une image en niveaux de gris, alors cela va agrandir les zones sombres de l’image.

- La dilatation : Pour chaque position de B sur l’image X, si au moins un des pixels de B fait partie de X, alors l’origine de B appartient à l’image générée. Donc à l’inverse, la dilatation d’une image va augmenter la présence de pixel noir sur celle-ci. Au contraire si on fait une dilatation sur une image en niveaux de gris, alors cela va agrandir les zones claires de l’image.

- L’ouverture va avoir pour but d’isoler les surfaces présentes dans l’image et de lisser les contours. Pour cela, on va réaliser une érosion par B puis une dilatation par la transposée de B (la transposée de B étant la symétrie de B par rapport à l’origine.). Si on fait une ouverture sur une image en niveaux de gris, alors cela va supprimer les petites zones claires de l’image.

- La fermeture aura pour but de recoller des morceaux de surfaces proches de manière à fermer des contours disjoints et de lisser les contours. Pour cela on réalise une dilatation par B de l’image puis une érosion par la transposée de B. Si on fait une fermeture sur une image en niveaux de gris, alors cela va supprimer les petites zones sombres de l’image.

Pour appliquer ces algorithmes à des images en couleurs, il faut utiliser la luminance qui correspond approximativement à : L = 0.3R + 0.59G + 0.11B Cependant, pour une image en niveaux de gris il n’y a pas besoin de faire ce calcul car cela correspond tout simplement à la valeur du gris. Dans le cas d’une image en niveaux de gris, on utilise souvent un élément structurant de type « disque horizontal ». On obtient donc :

Pour l’érosion on va alors vérifier si l’élément structurant se trouve dans la forme (c’est-à-dire sous la nappe de niveaux de gris) et pour la dilatation on va regarder si l’élément structurant se trouve dans le fond (c’est-à-dire au-dessus de la nappe de niveaux de gris). Où l’érosion correspond au minimum des luminances observées dans un voisinage et la dilatation au maximum des luminances observées dans un voisinage.

Filtrage fréquentiel

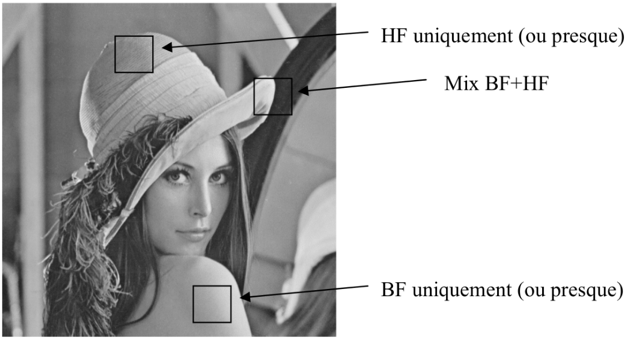
Le filtrage fréquentiel utilise la Transformée de Fourier pour obtenir le contenu fréquentiel de l’image. Ce contenu fréquentiel peut ensuite être décomposé en domaine de basses fréquences (faibles variations spatiales : zones homogènes) et de hautes fréquences (fortes variations spatiales : contours).

On aura donc les filtres passe-bas qui vont atténuer ou éliminer les hautes fréquences dans le domaine de Fourier : on obtient alors un lissage.

Et les filtres passe-haut qui vont cette fois-ci atténuer ou éliminer les basses fréquences : dans ce cas-là on va faire ressortir les contours des objets de l’image.

Enfin il existe également les filtres passe-bande qui élimine les composantes de fréquences intermédiaires.

Différences traitement d'image noir & blanc et couleurs

Les images en couleurs et celles en noir et blanc étant codées différemment en représentation matriciel, forcément le traitement d’une image en noir et blanc est bien plus simple puisqu’il n’y a qu’une seule valeur a modifié (le niveau de gris), alors que sur une image en couleur il faut modifier chacune des trois couleurs du pixel (dans le cas d’un codage RGB). Par exemple, pour faire l’histogramme cumulé d’une image en couleur, il faudra calculer la luminance de chaque pixel, alors que pour une image niveaux de gris il suffit de prendre la valeur du pixel.

Filtrage fréquentiel

Il existe actuellement plein d’algorithmes utilisant le filtrage fréquentiel. Dans presque tous ces algorithmes on va utiliser la Transformée de Fourier pour passer à une représentation de l’image dans le domaine fréquentiel. Il y a par exemple les simples algorithmes de filtre passe-bas et passe-haut qui ont été expliqués plus tôt. Mais il existe par exemple le filtre de Butterworth qui, plutôt que de couper nette les fréquences non voulues, va adoucir la transition. Ou encore le filtre de Gabor. Il s’agit d’une ellipse qui nous permettra donc de selectionner une direction dans laquelle on ne dégradera pas l’image (c’est-à-dire là ou les HF ne seront pas coupées).

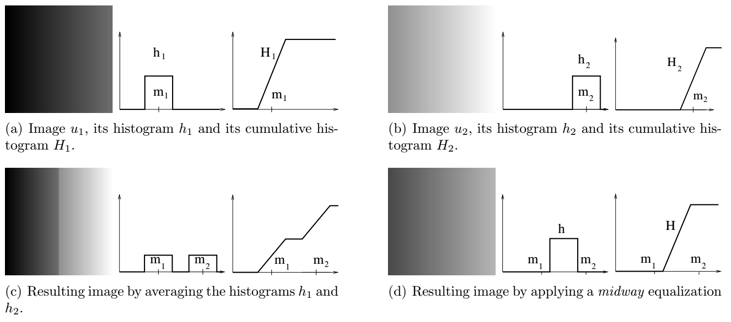
Midway Image Equalization

Le but de cet algorithme va être de donner à une image le même histogramme qu’une autre image en préservant le plus possible les niveaux de gris. Voici ce que l’on doit obtenir en principe avec cet algorithme :

Cet algorithme fonctionne aussi bien avec des images en niveaux de gris qu’avec des images en couleurs. L’utilisation de l’histogramme cumulé permet d’appliquer cet algorithme à des images de tailles différentes.

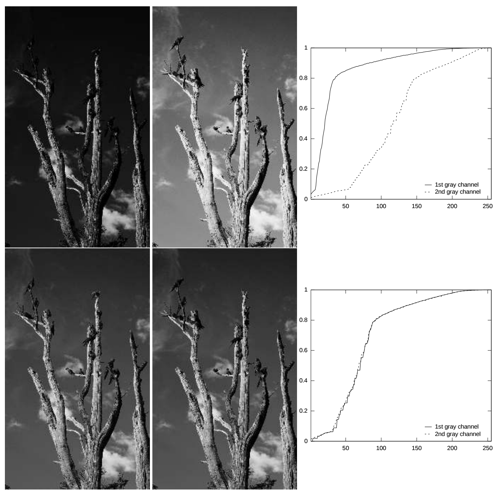
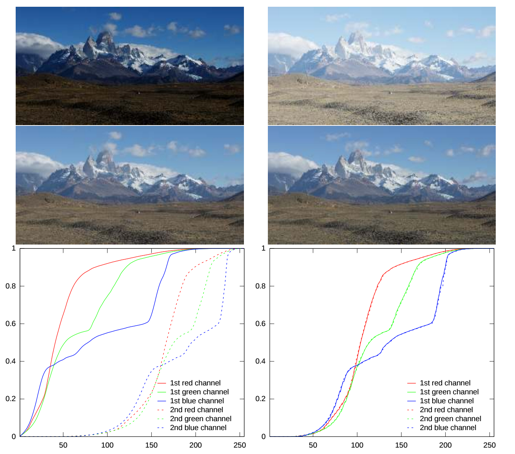
Pour illustrer l’efficacité et les limites de cet algorithme, voici ci-dessous quelques exemples : Cette méthode fonctionne bien avec des images en niveaux de gris d’une même scène mais avec une exposition à la lumière différente.

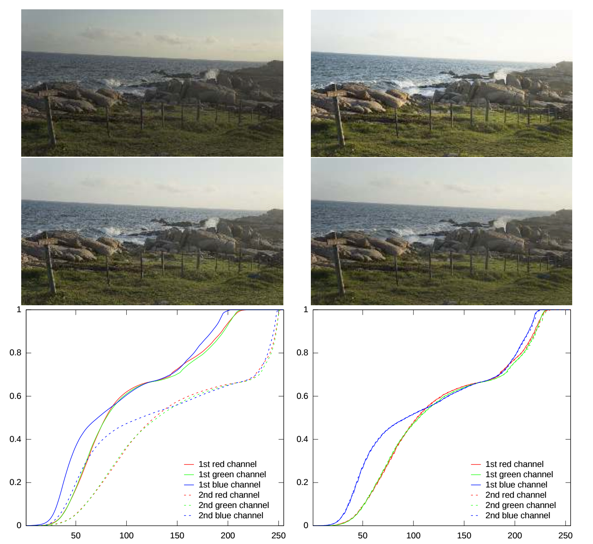
Par contre si les images sont différentes par exemple à cause d’un simple mouvement de l’appareil photo ou de l’objet photographié, alors cela peut modifier la répartition des niveaux de gris sur l’histogramme.

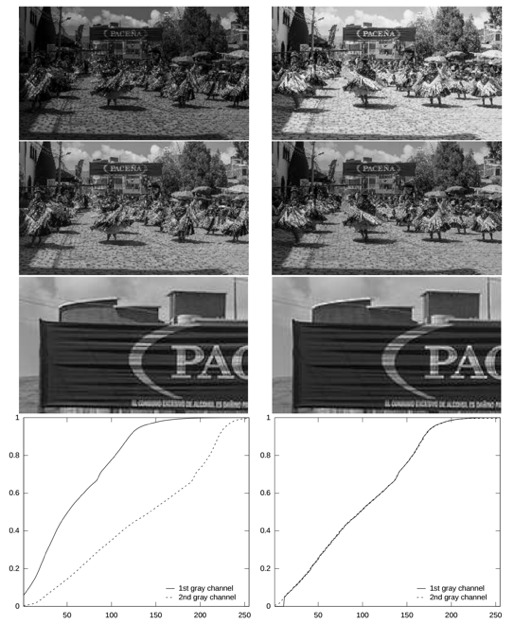
Pour les images en couleur d’une même scène mais encore une fois avec deux expositions différentes, appliquer l’égalisation moyenne aux trois canaux de couleurs indépendamment donne en général un bon résultat :

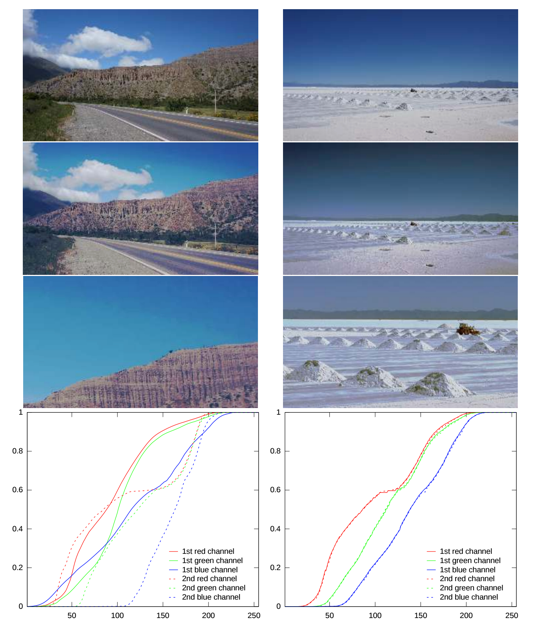
Si on utilise cet algorithme sur des images différentes contenant des couleurs différentes alors le résultat pourrait énormément modifier les couleurs de l’image. Dans ce cas-là on peut voir que les images obtenues n’ont pas des couleurs très naturelles mais le résultat n’est pas non plus irréaliste :

Le point fort de cet algorithme d’égalisation moyenne est qu’il s’adapte à des images de différentes tailles grâce à l’utilisation de l’histogramme cumulé :

J’ai ensuite écris cet algorithme à l’aide de Python. J’ai choisi de le créer sur Python car c’est l’outil de programmation qui a été le plus utilisé pendant l’année et c’est donc celui avec lequel je suis le plus à l’aise. Pour commencer j’ai récupéré un programme créer par Xavier Provençal pour un TP de Mathématique pour le numérique qui permet de manipuler des images en format PPM. Voici le programme en question :

#!/usr/bin/env python3
# -*- encoding: utf-8 -*-


###############################################################
#                                                             #
# MATH202 : Mathématiques pour le numérique II                #
#                                                             #
# Mini bibliothèque pour manipuler des images au format PPM.  #
#                                                             #
# Auteur : Xavier Provençal                                   #
#                                                             #
###############################################################

from collections import deque

class Image : 

    def __init__( self, filename ) :
        # Validation du fichier
        f = open( filename, 'r' )
        firstLine = f.readline()
        if firstLine != "P3\n" :
            raise ValueError( "[IMAGE] Initialisation depuis un fichier incompatible" )
        # Lecture des données
        d = deque()
        for l in f.readlines() :
            if l[0] != '#' :
                d.extend( map( int, l.split() ) )
        self._width = d.popleft()
        self._height = d.popleft()
        d.popleft() # on ignore la valeur max, on prend 255
        self._values = []
        while len(d) >= 3 :
            self._values.append( ( d.popleft(), d.popleft(), d.popleft() ) )

    def __repr__( self ) :
        return "Image de dimensions {} x {}".format( self._width, self._height )

    def save( self, filename ) :
        assert( filename[-4:] == ".ppm" )
        f = open( filename, 'w' )
        f.write( "P3\n" )
        f.write( "{} {}\n255\n".format( self._width, self._height ) )
        for y in range( self.hauteur ) :
            for x in range( self.largeur ) :
                c = self.getPixel( x,y )
                f.write( '{} {} {}\n'.format( c[0], c[1], c[2] ) )
        f.close()

    @property
    def hauteur( self ) :
        return self._height

    @property
    def largeur( self ) :
        return self._width

    def getPixel( self, x, y ) :
        return self._values[ x + self._width*y ]

    def setPixel( self, x, y, couleur ) :
        self._values[ x + self._width*y ] = couleur

Ensuite, en me servant du programme précédent j’ai fait le programme suivant qui s’applique aux images en format PPM et en noir et blanc ou dans l’espace RGB :

def midway_equalization_color(image1, image2):
    """Pour image en format ppm et en noir et blanc"""
    u1 = Image(image1)
    u2 = Image(image2)
    l1 = u1.largeur
    h1 = u1.hauteur
    l2 = u2.largeur
    h2 = u2.hauteur
    H1r = [0]*256
    H2r = [0]*256
    H1g = [0]*256
    H2g = [0]*256
    H1b = [0]*256
    H2b = [0]*256
    #calcul de l'histogramme de chaque image
    for i in range (1,l1):
        for k in range (1,h1):
            c = u1.getPixel( i, k )
            r = c[0]
            g = c[1]    
            b = c[2]
            H1r[r] += 1/(l1*h1)
            H1g[g] += 1/(l1*h1)
            H1b[b] += 1/(l1*h1)
    for i in range (1,l2):
        for k in range (1,h2):
            c = u2.getPixel( i, k )
            r = c[0]
            g = c[1]    
            b = c[2]
            H2r[r] += 1/(l2*h2)
            H2g[g] += 1/(l2*h2)
            H2b[b] += 1/(l2*h2)
    
    #calcul de l'histogramme cumulé de chaque image
    Hc1r = [H1r[0]]
    Hc1g = [H1g[0]]
    Hc1b = [H1b[0]]
    Hc2r = [H2r[0]]
    Hc2g = [H2g[0]]
    Hc2b = [H2b[0]]
    for i in range (1,len(H1r)):
        Hc1r.append(H1r[i]+Hc1r[i-1])
        Hc1g.append(H1g[i]+Hc1g[i-1])
        Hc1b.append(H1b[i]+Hc1b[i-1])
    for i in range (1,len(H2r)):
        Hc2r.append(H2r[i]+Hc2r[i-1])
        Hc2g.append(H2g[i]+Hc2g[i-1])
        Hc2b.append(H2b[i]+Hc2b[i-1])
    
    #calcul de la fonction de contraste f12
    f12r = [0]*256
    f12g = [0]*256
    f12b = [0]*256
    l = 0
    for i in range (len(Hc1r)):
        while (Hc1r[i] > Hc2r[l]) and (l<255):
            l += 1
        f12r[i] = int((1/2)*(i+l))
    l = 0
    for i in range (len(Hc1g)):
        while (Hc1g[i] > Hc2g[l]) and (l<255):
            l += 1
        f12g[i] = int((1/2)*(i+l))
    l = 0
    for i in range (len(Hc1b)):
        while (Hc1b[i] > Hc2b[l]) and (l<255):
            l += 1
        f12b[i] = int((1/2)*(i+l))
   
    #calcul de la fonction de contraste f21
    f21r = [0]*256
    f21g = [0]*256
    f21b = [0]*256
    l = 0
    for i in range (len(Hc2r)):
        while (Hc2r[i] > Hc1r[l]) and (l<255):
            l += 1
        f21r[i] = int((1/2)*(i+l))
    l = 0
    for i in range (len(Hc2g)):
        while (Hc2g[i] > Hc1g[l]) and (l<255):
            l += 1
        f21g[i] = int((1/2)*(i+l))
    l = 0
    for i in range (len(Hc2b)):
        while (Hc2b[i] > Hc1b[l]) and (l<255):
            l += 1
        f21b[i] = int((1/2)*(i+l))
  
    #application du contraste de f12 sur u1
    for i in range (l1):
        for k in range (h1):
            c = u1.getPixel(i,k)
            r = c[0]
            g = c[1]
            b = c[2]
            r2 = f12r[r]
            g2 = f12g[g]
            b2 = f12b[b]

            u1.setPixel(i,k,(r2,g2,b2))
    u1.save('out1.ppm')

    #application du contraste de f21 sur u2
    for i in range (l2):
        for k in range (h2):
            c = u2.getPixel(i,k)
            r = c[0]
            g = c[1]
            b = c[2]
            
            r2 = f21r[r]
            g2 = f21g[g]
            b2 = f21b[b]

            u2.setPixel(i,k,(r2,g2,b2))
    u2.save('out2.ppm')