Valeurs de Sprague-Grundy pour le jeu de Wythoff
Étudiant : Nolann SANMARTI
Tuteur : Stéphane TAVENAS
Jeu de Nim (Jeu simple à 1 ligne)
Description du jeu
Le jeu de Nim est un jeu à deux joueurs qui se joue en tour par tour.
Des allumettes sont disposées sur une table, en ligne, et chaque joueur retire entre 1 et 3 allumettes de cette ligne.
La personne qui retire la dernière allumette est perdante.
- Exemple avec 12 allumettes :
- Le joueur A retire 2 allumettes. Il en reste 10.
- Le joueur B retire 3 allumettes. Il en reste 7.
- Le joueur A retire 1 allumette. Il en reste 6.
- Le joueur B retire 2 allumettes. Il en reste 4.
- Le joueur A retire 3 allumettes. Il en reste 1.
- Le joueur B perd car il est forcé de prendre la dernière allumette.
Stratégie de jeu
Ce jeu est un jeu avantageant le premier joueur par le fait qu'une stratégie gagnante est présente.
En effet, on sait que chaque joueur ne peut enlever qu'entre 1 et 3 allumettes, donc en ayant 5 allumettes sur le plateau :
- Si le joueur A enlève 1 allumette, on aura alors 4 allumettes sur le plateau et le joueur B enlèvera 3 allumettes ;
- Si le joueur A enlève 2 allumettes, on aura alors 3 allumettes sur le plateau et le joueur B enlèvera 2 allumettes ;
- Si le joueur A enlève 3 allumettes, on aura alors 2 allumettes sur le plateau et le joueur B enlèvera 1 allumette.
On remarque que cette stratégie peut être appliquée pour passer de 9 à 5, de 13 à 9, et ainsi de suite.
En gardant cet écart de 4, on aura une suite de positions perdantes permettant ainsi en se positionnant dessus de faire perdre l'adversaire.
Suite : 1,5,9,13,17,...
Jeu de Wythoff (Jeu à 2 lignes)
Description du jeu
Le jeu de Wythoff est une variante du jeu de Nim où l'on va rajouter un jeu d'allumettes.
Les règles sont également un peu complexifiés pour s'adapter à 2 jeux :
- On peut retirer le nombre d'allumettes qu'on veut dans 1 seul des jeux ;
- On peut retirer le nombre d'allumettes qu'on veut dans les 2 jeux.
À l'inverse du jeu d'avant, le but est de retirer la dernière allumette des jeux (Les deux jeux vides).
Pour simplifier la lecture, on va écrire ces valeurs comme des coordonnées de tableau.
Le nombre d'allumettes dans le 1er paquet sera x // Le nombre d'allumettes dans le 2e paquet sera y // On aura donc (x,y) le nombres d'allumettes dans chacun des paquets.
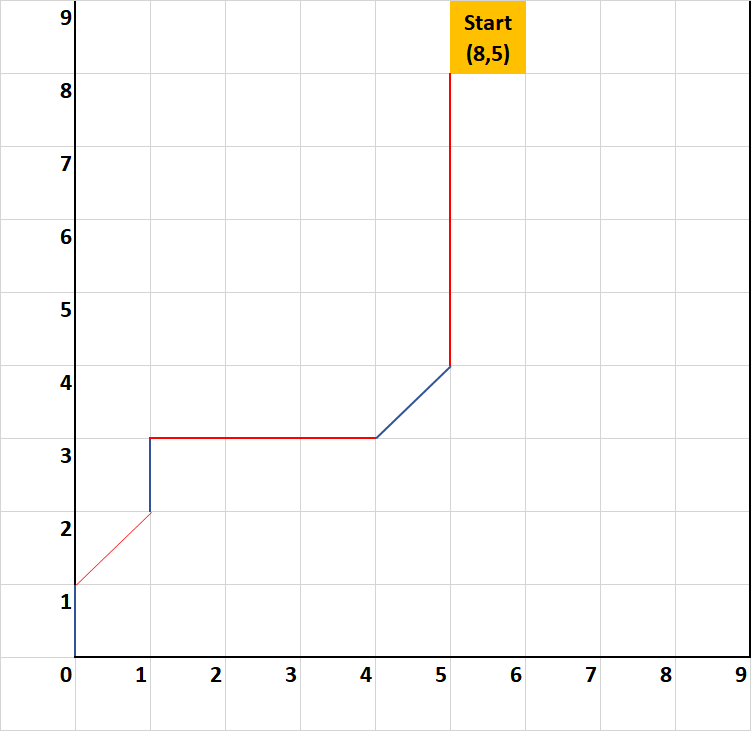
Exemple avec (8,5) :
- Le joueur A enlève 4 à x. On se retrouve en (4,5).
- Le joueur B enlève 1 à x et y. On se retrouve en (3,4).
- Le joueur A enlève 3 à y. On se retrouve en (3,1).
- Le joueur B enlève 1 à x. On se retrouve en (2,1).
- Le joueur A enlève 1 à x et y. On se retrouve en (1,0).
- Le joueur B gagne en retirant 1 à x. On se retrouve en (0,0).
Stratégie de jeu
Trouver de façon expérimentale
Ce jeu avantage également le premier joueur avec une stratégie gagnante.
Cette stratégie gagnante est un peu plus difficile à cerner aux premiers abords, mais rapidement applicable après avoir l'astuce :
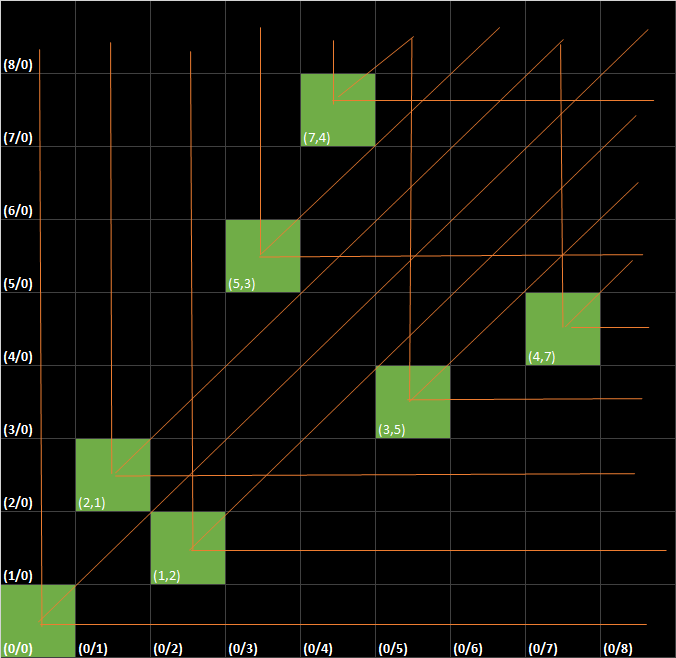
On va commencer par colorier en vert la case (0,0) qui est l'objectif, puis colorier en noir les cases alignés verticalement, horizontalement et en diagonale.
Les cases avec la valeur de x ou y la plus petite seront en vert, puis on colorie également en noir les cases alignés verticalement, horizontalement et en diagonale.
On répète ce processus jusqu'à atteindre les bords du plateau sans cases libres.
Trouver par le calcul (Algorithme)
On va prendre un emplacement qui stockera des nombres déjà utilisés => Poubelle [n1,n2,n3,...]
On prend un autre emplacement qui stockera les positions gagnantes => Positions [(X1,Y1),(X2,Y2),(X3,Y3),...]
On va définir une variable qui est égale à la n-ième position gagnante => Occurence (K)
On va commencer à compter de 1 en 1 à partir de 1 => I. (On sait déjà que la position (0,0) est gagnante du fait que c'est le but)
- Si le nombre est déjà dans la poubelle, on continue de compter... => I+1
- Sinon :
- On entre I dans les positions gagnantes en X et on entre le nombre I+K en Y => Positions : Add >> (I,I+K)
- Les valeurs de I et I+K sont envoyés en poubelle
- On ajoute 1 à K => K : K+1
- I retourne à 1. => I : 1.
/!\ Si I ou I+K est plus grand que la taille de grille, on finit la boucle sans rien ajouter
Quand on ressort les valeurs de Positions, il faut les ressortir en deux fois : Une fois à l'endroit et une fois en permutant X et Y ( Symétrie : (X1,Y1),(Y1,X1),(X2,Y2),(Y2,X2),... )
Robot jouant parfaitement
Principe
Le robot doit pouvoir jouer contre un humain sans le laisser gagner.
Dans cette version, le robot laisse une chance au joueur de pouvoir gagner s'il se déplace tout le temps sur une position perdante.
Algorithme brut
from matplotlib import pyplot as plt
import random as rnd
#longueur sert de taille de grille de jeu (ex: grille 10x10 => longueur = 10)
#Vérifie si le pion n'est pas directement aligné à (0,0) faisant gagner systématiquement le joueur 1 sans jeu.
def conditionPion(xPos,yPos):
if(xPos == 0 or yPos == 0):
return True
elif(xPos == yPos):
return True
else:
return False
def Pion(longueur):
xposPion = rnd.randint(0, longueur)
yposPion = rnd.randint(0, longueur)
return (xposPion,yposPion)
def grille(longueur,On):
## DESSIN DE LA GRILLE ##
valeursX = [0,longueur,longueur]
valeursY = [longueur,longueur,0]
for i in range(longueur-1):
valeursX += [longueur-1-i]*3
valeursY += [0,longueur,0]
valeursX += [0]
valeursY += [0]
for i in range(longueur-1):
valeursX += [0,longueur,0]
valeursY += [longueur-1-i]*3
valeursX += [0]
valeursY += [longueur]
plt.plot(valeursX,valeursY)
plt.plot(0,0,'ro')
#########################
## AFFICHAGE DES POSITIONS GAGNANTES ##
if(On):
positionsGagnantes = posGagnantes(longueur)
for i in range(len(positionsGagnantes)):
plt.plot(positionsGagnantes[i][0],positionsGagnantes[i][1], 'yo')
#######################################
## AJOUT DU PION ##
xposPion,yposPion = Pion(longueur)
while(conditionPion(xposPion,yposPion)):
xposPion,yposPion = Pion(longueur)
plt.plot(xposPion, yposPion, 'bo')
###################
## AFFICHAGE DE LA GRILLE ##
plt.title('Jeu de Whytoff')
plt.show()
############################
return (xposPion,yposPion)
def Jouer(opt,longueur,On):
## Récupération de la position des pions ##
xposPion,yposPion = grille(longueur,On)
Joueur = 0
MoveAutorise = ["Gauche","Bas","Diagonale"]
PositionX = xposPion
PositionY = yposPion
###########################################
## Partie ##
while(PositionX > 0 or PositionY > 0):
print("Position du pion : (" + str(PositionX) + "," + str(PositionY) + ")")
deplAutorise = ""
for i in range(len(MoveAutorise)):
deplAutorise += MoveAutorise[i]
if(i != len(MoveAutorise)-1):
deplAutorise += ", "
typeMove=input("Déplacement dans quel sens ?\r\n*Déplacements autorisés : " + deplAutorise + "\r\n")
while(typeMove not in MoveAutorise):
typeMove=input("Mouvement non autorisé.\r\nDéplacement dans quel sens ?\r\n*Déplacements autorisés : " + deplAutorise + "\r\n")
## Déplacement à gauche ##
if(typeMove == "Gauche"):
valMove=int(input("De combien voulez-vous vous déplacer à gauche ?\r\n*Vous pouvez vous déplacer de 1 à " + str(PositionX) + " cases.\r\n"))
while(valMove < 0 or valMove > PositionX):
valMove=int(input("Valeur incorrecte.\r\nDe combien voulez-vous vous déplacer à gauche ?\r\n*Vous pouvez vous déplacer de 1 à " + str(PositionX) + " cases.\r\n"))
PositionX -= valMove
## Déplacement en bas ##
elif(typeMove == "Bas"):
valMove=int(input("De combien voulez-vous vous déplacer en bas ?\r\n*Vous pouvez vous déplacer de 1 à " + str(PositionY) + " cases.\r\n"))
while(valMove < 0 or valMove > PositionY):
valMove=int(input("Valeur incorrecte.\r\nDe combien voulez-vous vous déplacer en bas ?\r\n*Vous pouvez vous déplacer de 1 à " + str(PositionY) + " cases.\r\n"))
PositionY -= valMove
## Déplacement en diagonale ##
else:
valMove=int(input("De combien voulez-vous vous déplacer en diagonale ?\r\n*Vous pouvez vous déplacer de 1 à " + str(min(PositionX,PositionY)) + " cases.\r\n"))
while(valMove < 0 or valMove > min(PositionX,PositionY)):
valMove=int(input("Valeur incorrecte.\r\nDe combien voulez-vous vous déplacer en diagonale ?\r\n*Vous pouvez vous déplacer de 1 à " + str(min(PositionX,PositionY)) + " cases.\r\n"))
PositionX -= valMove
PositionY -= valMove
## Déplacements autorisés ##
if(PositionX != 0 or PositionY != 0):
if(PositionX == 0):
MoveAutorise.remove("Gauche")
if("Diagonale" in MoveAutorise):
MoveAutorise.remove("Diagonale")
if(PositionY == 0):
MoveAutorise.remove("Bas")
if("Diagonale" in MoveAutorise):
MoveAutorise.remove("Diagonale")
print()
print("Type de mouvement :", typeMove, "\r\nValeur de mouvement :", valMove)
print()
## Deux humains ##
if(opt == 1):
if(PositionX != 0 or PositionY != 0):
print("Au tour de l'adversaire !")
print()
Joueur += 1
Joueur = Joueur%2
else:
print("Fin de partie ! Le joueur " + str(Joueur+1) + "remporte la partie.")
## Un humain et un Robot ##
else:
if([PositionX,PositionY] in posGagnantes(longueur)):
typeMove = rnd.choice(MoveAutorise)
if(typeMove == "Gauche"):
valMove = rnd.randint(1, PositionX)
print('Le Bot s\'est déplacé de ' + str(valMove) + ' vers la gauche.')
PositionX -= valMove
elif(typeMove == "Bas"):
valMove = rnd.randint(1, PositionY)
print('Le Bot s\'est déplacé de ' + str(valMove) + ' vers le bas.')
PositionY -= valMove
else:
valMove = rnd.randint(1, min(PositionX,PositionY))
print('Le Bot s\'est déplacé de ' + str(valMove) + ' en diagonale.')
PositionX -= valMove
PositionY -= valMove
else:
if not(PositionX == 0 and PositionY == 0):
if(PositionX == 0 or PositionY == 0 or PositionX == PositionY):
PositionX = 0
PositionY = 0
print("J'ai gagné en allant vers (0,0) !! Dommage D:")
else:
positionsGagnantes = posGagnantes(max(PositionX,PositionY))
print(posGagnantes(max(PositionX,PositionY)))
i=0
state = 0
if(positionsGagnantes != None):
while(i<len(positionsGagnantes)):
if(PositionY == positionsGagnantes[i][1] and PositionX > positionsGagnantes[i][0]):
PositionX = positionsGagnantes[i][0]
state = 1
print("J'ai joué vers la gauche à la position (" + str(PositionX) + "," + str(PositionY) + ")")
break
elif(PositionX == positionsGagnantes[i][0] and PositionY > positionsGagnantes[i][1]):
PositionY = positionsGagnantes[i][1]
state = 1
print("J'ai joué vers le bas à la position (" + str(PositionX) + "," + str(PositionY) + ")")
break
else:
i += 1
if(state == 0):
while not([PositionX,PositionY] in positionsGagnantes and [PositionY,PositionX] in positionsGagnantes):
PositionX -= 1
PositionY -= 1
print("J'ai joué en diagonale à la position (" + str(PositionX) + "," + str(PositionY) + ")")
else:
print("Bravo pour avoir gagné contre moi :D")
## Déplacements autorisés ##
if(PositionX != 0 or PositionY != 0):
if(PositionX == 0):
MoveAutorise.remove("Gauche")
if("Diagonale" in MoveAutorise):
MoveAutorise.remove("Diagonale")
if(PositionY == 0):
MoveAutorise.remove("Bas")
if("Diagonale" in MoveAutorise):
MoveAutorise.remove("Diagonale")
#Calcul des positions gagnantes
def posGagnantes(longueur):
positionsGagnantes = [] #Positions qui font que le joueur gagnera systématiquement en se déplaçant de l'une à l'autre
nombresUtilises = [] #Coordonnée déjà utilisée dans l'une des positions gagnantes
i = 1
while(i < longueur): #Strictement inférieur car on ne peut pas avoir une position (longueur,longueur) gagnante.
if i not in nombresUtilises:
ordonne = i+(len(positionsGagnantes)//2)+1
if(ordonne > longueur):
return positionsGagnantes
else:
nombresUtilises += [i,ordonne]
positionsGagnantes += [[i,ordonne]]
positionsGagnantes += [[ordonne,i]]
i = 1
else:
i+=1
return positionsGagnantes
Valeurs de Sprague-Grundy appliquées au jeu de Wythoff
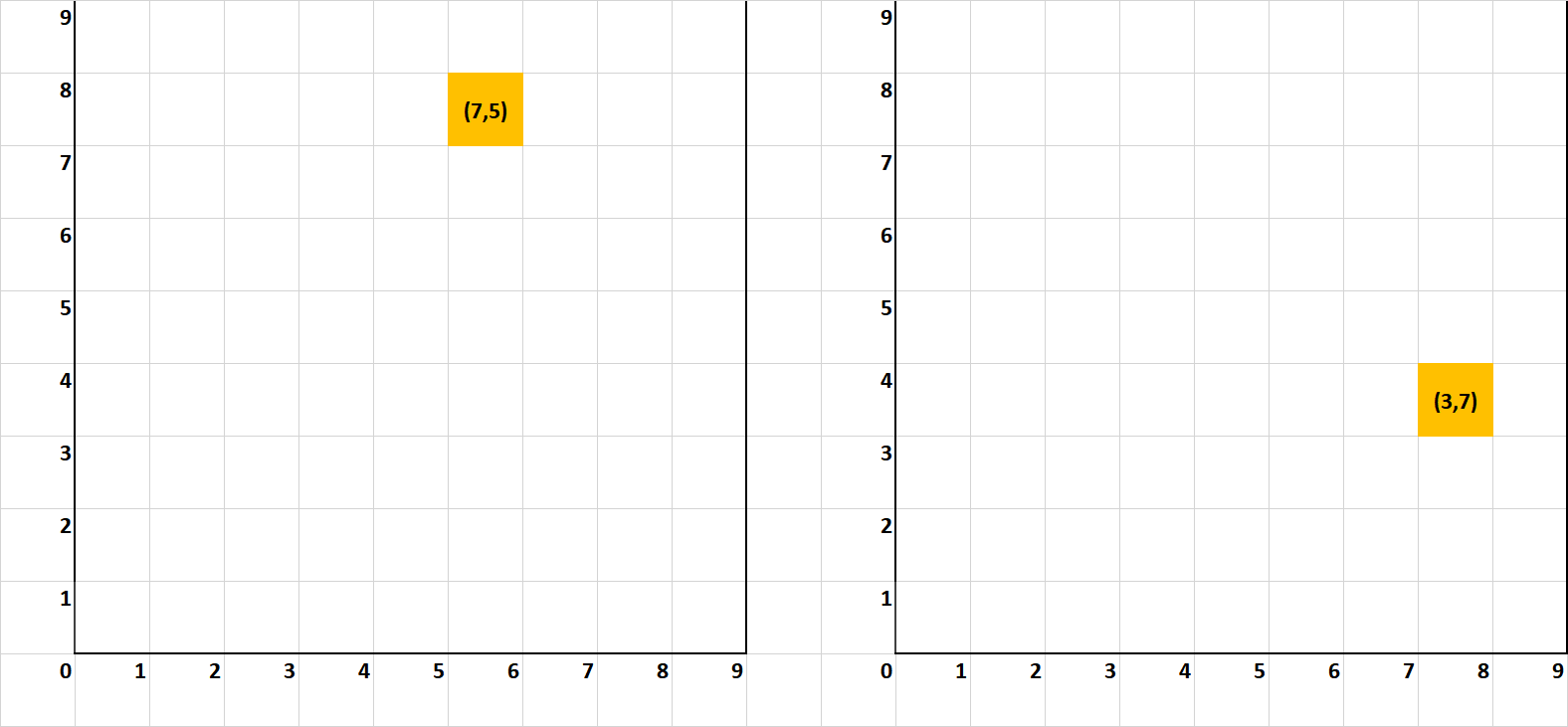
On va maintenant jouer avec 2 plateaux de 2 lignes (4 lignes) fonctionnant comme un jeu de Wythoff.
On pourra jouer que sur un seul des deux par tour.
Le gagnant est celui qui retire la toute dernière allumette ( Arrive en ((0,0)(0,0)) )
Principe
La valeur de Sprague-Grundy d'une case est la plus petite valeur qui n'apparait pas à gauche, en bas et en diagonale de cette case.
Exemple pour une grille de 9x9 :
Calcul
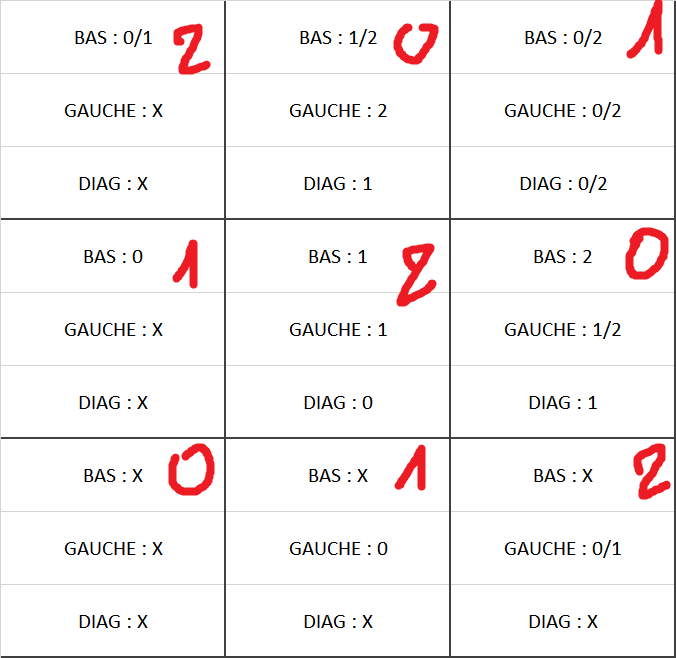
Pour les calculer automatiquement, il faut entrer dans 3 tableaux différents les nombres déjà présents sur les cases du bas, gauche et diagonale puis prendre la valeur entière la plus basse qui n'est dans aucune des listes.
On les calcule (et attribue) de gauche à droite et de bas en haut.
Exemple sur un tableau de 3x3 :
VISI201 CMI : visite de laboratoire (Retour à la page des projets)