« Calculabilité et modèles de calcul » : différence entre les versions
(Page créée avec « '''1-Calculabilité pour des fonctions de N → N''' Une question fondamentale de l’informatique théorique est de déterminer si un problème donné peut ou non être ... ») |
Aucun résumé des modifications |
||
| (4 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
= Calculabilité pour des fonctions de N → N = |
|||
Les cours d’informatique peuvent donner l’impression que pour chaque problème on peut trouver un algorithme de solution. Une question fondamentale de l’informatique théorique est de déterminer si un problème donné peut être ou non résolu par d’un ordinateur (par une procédure effective). En particulier se pose la question de déterminer si une fonction donnée peut être calculée au moyen d’un algorithme. |
|||
La calculabilité qui est une branche de la logique et de l'informatique théorique, permet de définir ce qui est calculable et ce qui ne l’est pas et nous montrera que pour de nombreux problèmes il n’existe pas d’algorithme. La calculabilité nous aide à comprendre les limites de ce que nous pouvons calculer et de ce que nous pouvons faire avec un ordinateur. |
|||
Une question fondamentale de l’informatique théorique est de déterminer si un problème donné peut ou non être résolu au moyen d’un ordinateur (par une procédure effective). En particulier se pose la question de déterminer si une fonction donnée (à arguments et valeurs entiers) peut être calculée au moyen d’un algorithme. La question ainsi formulée est indépendante de la machine utilisée, de ses ́éventuelles performances, de la mémoire disponible ou encore du langage de programmation employé. |
|||
La calculabilité est une branche de la logique et de l'informatique théorique. |
|||
Elle permet de définir ce qui est calculable et ce qui ne l’est pas et nous montrera que pour de nombreux problèmes il n’existe pas d’algoritme. La calculabilité nous aide à comprendre les limites de ce que peuvent faire des ordinateurs. |
|||
Une fonction f avec un argument x est calculable s’il existe un algoritme pour calculer f(x) peu importe le nombre d'étapes. |
|||
== Fonction calculable == |
|||
''Qu'est-ce qui est programmable ?'' |
|||
Une fonction f avec un argument x est calculable s’il existe un algorithme pour calculer f(x) peu importe le nombre d'étapes. |
|||
Certaines de ces fonctions sont programmables, d'autres peut-être pas. Les fonctions programmables sont aussi appelées des fonctions calculables ou récursives |
|||
Les fonctions calculables sont également appelées fonctions récursives ou fonctions programmables. |
|||
Nous connaissons de très nombreuses fonctions calculables. En particulier toutes celles que nous avons programmées ! La plupart des fonctions que l'on rencontre naturellement en mathématiques le sont : |
|||
Nous connaissons de très nombreuses fonctions calculables. En particulier toutes celles que nous avons programmées ! La plupart des fonctions que l'on rencontre en mathématiques le sont : |
|||
- somme, différence, produit, égalité, division, puissance…union,intersection,quantification bornée… |
- somme, différence, produit, égalité, division, puissance…union, intersection, quantification bornée… |
||
- PGCD ( |
- PGCD (algorithme d’Euclide) |
||
- |
-Programmes informatiques qui s'arrêtent. |
||
. Une fonction non calculable est donc une fonction f pour laquelle aucun programme P n'existe qui donne en sortie la valeur f(n) lorsqu'on lui donne en l'entier n en entrée, et ceci pour tout n ∈ N. |
|||
== Fonction non calculable == |
|||
-problème de l'arrêt : execution interminable d’un programme |
|||
Une fonction non calculable est donc une fonction pour laquelle aucun programme n’existe. Les deux fonctions non calculables les plus connues sont : |
|||
- problème de l'arrêt c’est-à-dire l’exécution interminable d’un programme. |
|||
'''-Castor affairé:''' Il s'agit d'une fonction bien définie, ayant des valeurs pour chaque entier, mais dont on ne peut pas calculer la valeur.Un castor affairé est, en théorie de la calculabilité, une machine de Turing qui atteint une « activité opérationnelle » maximale (comme le nombre de pas effectués ou le nombre de symboles écrits avant son arrêt) parmi toutes les machines de Turing d'une certaine classe. Celles-ci doivent satisfaire certaines spécifications et doivent s'arrêter après être lancées sur un ruban vierge.Une fonction du castor affairé quantifie cette activité maximale pour une machine de Turing à n états ; ce type de fonction n'est pas calculable. En fait, au bout d'un certain point, une fonction du castor affairé croît plus rapidement que n'importe quelle fonction calculable. Déterminer le castor affairé pour un ensemble de machines de Turing à n états donnés est un problème insoluble algorithmiquement ; en pratique, on ne peut même pas espérer le résoudre pour un nombre n au-delà de 10. Le concept, introduit en 1962 par le mathématicien hongrois Tibor Radó, est l'un des premiers exemples connus de fonction non calculable. |
|||
- « Castor affairé » : ce concept a été introduit en 1962 par le mathématicien hongrois Tibor Radó. C’est l'un des premiers exemples connus de fonction non calculable. |
|||
''Étudions maintenant le nombre de fonctions calculables.'' |
|||
Un « castor affairé » est une machine de Turing à n états qui écrit un maximum de « 1 » sur le ruban avant de s’arrêter. Au-delà d’un n trop élevé on ne peut pas déterminer quel est le castor affairé pour un nombre d’états même avec un ordinateur puissant. |
|||
Il est clair qu'il y en a une infinité. Il suffit de considérer l'infinité des fonctions constantes. De plus, il ne peut pas y avoir plus de fonctions calculables qu'il n'y a de programmes,puisqu'à chaque fonction calculable lui correspond par définition un programme.Donc l’infinité des fonctions calculables n’est pas plus grande que celle des programmes. Et comme l’infini dénombrable est le plus petit infini, on en déduit que l’ensemble des fonctions calculables est infini dénombrable. |
|||
D'autre part il y a une infinité non dénombrable de fonctions de N dans N. Il existe donc des fonctions non calculables. |
|||
On peut même ajouter que dans un certain sens les fonctions non calculables sont infiniment plus nombreuses que les fonctions calculables. Les fonctions non calculables sont la règle générale, et les fonctions calculables l'exception. |
|||
== Dénombrement de fonction calculable == |
|||
Il existe une infinité de fonctions, l’ensemble des fonctions n’est donc pas dénombrable. Par contre l’ensemble des programmes, lui, est dénombrable. Il existe donc beaucoup plus de fonctions que de programmes par conséquent il existe un nombre infini de fonctions qui ne sont pas calculables par un programme ce qui revient à dire que la plus grande partie des problèmes que l’on peut définir en mathématiques n’ont pas de solution algorithmique. |
|||
'''2-Modèles de calcul''' |
|||
= Modèles de calcul = |
|||
'''Machine de Turring :''' Cette machine est inventé de son nom de Alan Turing en 1936. Elle va definir la notion de fonction calculable.C'est une machine abstraite et mathématique.On peut executé n'importe quel programme que l'on peut executé sur un ordinateur, on peut aussi simulé n'importe quel automate fini ou à pile.Une machine de Turing est composé de plusieurs éléments : - d'une unité de contrôle(registre d'état et table d'action), d'un ruban inifini divisé en cases et d'une tête de lecture/ écriture.L'unité de contrôle permet la mémorisation de l'état courant et dit à la machine dans quel sens se deplacer à la tête de lecture/ecriture.Le ruban joue le rôle de périphérique entrée, sortie. Vierge au debut on y inscrit les données que traite le programme.La tête lecture/ecriture lit le contenu de la case sur laquelle elle se trouve elle permit de l'effacer ou ecrit un nouveau symbole. Elle peut se déplacer à gauche ou à droite.A la fin du programme ,les mots sur le ruban consituent le resultat final du calcul. |
|||
Le fonctionnement depend de deux paramètres : symbole lu c'est la case où se trouve la tête de lecture/ecriture et l'état de la machine. Ce couple va exécuté ce que demande le programme. |
|||
La machine de Turing est un sextuplet(Q, Σ, Γ, δ, q0, F) : |
|||
== Machine de Turing == |
|||
[[Fichier:Lego_Turing_Machine.jpg]] |
|||
Ci dessus une machine de Turring réalisé en lego à Lyon. |
|||
Cette machine a été inventée par Alan Turing en 1936. Elle va définir la notion de fonction calculable. C’est une machine abstraite et mathématique. |
|||
On peut exécuter n'importe quel programme que l'on peut exécuter sur un ordinateur, on peut aussi simulé n'importe quel automate fini ou à pile. |
|||
Une machine de Turing est composée de plusieurs éléments : |
|||
- d'une unité de contrôle (registre d'état et table d'action) |
|||
- d'un ruban infini divisé en cases |
|||
- d'une tête de lecture/ écriture. |
|||
L'unité de contrôle permet la mémorisation de l'état courant et dit à la machine dans quel sens se déplacer à la tête de lecture/écriture. |
|||
Le ruban joue le rôle de périphérique entrée, sortie. Vierge au début on y inscrit les données que traite le programme. |
|||
La tête lecture/écriture lit le contenu de la case sur laquelle elle se trouve elle permet de l'effacer ou écrit un nouveau symbole. Elle peut se déplacer à gauche ou à droite. |
|||
A la fin du programme, les mots sur le ruban constituent le résultat final du calcul. |
|||
Le fonctionnement dépend de deux paramètres : du symbole lu (c'est la case où se trouve la tête de lecture/écriture) et de l'état de la machine. Ce couple va exécuter ce que demande le programme. |
|||
La machine de Turing est un sextuplé (Q, Σ, Γ, δ, q0, F) : |
|||
Q est un ensemble fini d’états. |
Q est un ensemble fini d’états. |
||
| Ligne 40 : | Ligne 66 : | ||
Σ est l’alphabet (fini) d’entrée. |
Σ est l’alphabet (fini) d’entrée. |
||
Γ est l’alphabet (fini) du ruban |
Γ est l’alphabet (fini) du ruban. |
||
δ : Q × Γ → Q × Γ × {G, D, I} est la fonction de transition. |
δ : Q × Γ → Q × Γ × {G, D, I} est la fonction de transition. |
||
| Ligne 47 : | Ligne 73 : | ||
F ⊆ Q est l’ensemble des états accepteurs. |
F ⊆ Q est l’ensemble des états accepteurs. |
||
Exemple d'utilisation de Turing : |
Exemple d'utilisation de Turing : |
||
[https://interstices.info/jcms/nn_72391/comment-fonctionne-une-machine-de-turing |
[https://interstices.info/jcms/nn_72391/comment-fonctionne-une-machine-de-turing |
||
] |
|||
'''Automate cellulaire ''': Un automate cellulaire c'est un objet mathématique que l'on peut étudier aussi en informatique. Il évolue par étape et selon des règles plus ou moins simple. Il est constitué d'une grille et de plusieurs états, souvent 2 : mort ou en vie. |
|||
Cet objet mathématique provient des travaux de John Von Neumann et Stanislaw Ulaw en 1950 qui voulaient savoir comment se comportait une structure artifcielle, c'est à dire comme les etres vivants. Elles constituent donc aussi un modèle de calcul. |
|||
== Automate cellulaire == |
|||
Un automate cellulaire très connu est le jeu de la vie.Autre automate cellulaire: L'automate d'Ulman, L'automate Neige extraterrestre des dérivés du jeu de la vie. |
|||
[[Fichier:canon.png]] |
|||
'''Jeu de la vie ''': Il est inventé en 1970 par John Conway ce n'est pas réelement un jeu mais plutot un automate cellulaire qui est représenté sur une grille( un damier) dont les cellules sont blanches pour l'etat 'mort' et noir pour l'etat 'vivant. |
|||
Le but est de faire reproduire, disparaître ou survivre les cellules. Chaque cellules comporte autour d'elles 8 cellules. |
|||
Ci dessus le canon planeur réalisé à l'aide de python. |
|||
'''3-Jeu de la vie en pratique''' |
|||
Un automate cellulaire est un objet mathématique que l'on peut étudier aussi en informatique. Il évolue par étape et selon des règles plus ou moins simples. |
|||
''Les règles du jeu de la vie sont les suivantes :'' |
|||
Il est constitué d'une grille et de plusieurs états, souvent 2 : mort ou en vie. |
|||
Cet objet mathématique provient des travaux de John Von Neumann et Stanislaw Ulaw en 1950 qui voulaient comprendre comment se comportait une structure artificielle, c'est à dire comme les êtres vivants. Elles constituent donc aussi un modèle de calcul. |
|||
Les cellules qui survivent sont celles qui ont 2 ou 3 cellules adjacentes. |
|||
L’automate cellulaire le plus connu est le jeu de la vie. On peut citer également L'automate d'Ullman et l’automate Neige extraterrestre des dérivés du jeu de la vie. |
|||
Les celllles qui passent a l'état 'mort' sont celles ayant 4 ou plus cellules ajdcentes ou celle n'ayant une ou aucune cellule adjacentes. |
|||
Les cellules qui pasent à l'état 'vie' sont celles ayant exactement 3 cellules adjacentes. |
|||
== Jeu de la vie == |
|||
Toutes les naissances et toutes les morts ont lieu en même temps au cours d'une génération. |
|||
Un site avec des exemples d'oscillations, des formes stables, des pulsars... |
|||
[http://www.cypris.fr/loisirs/le_jeu_de_la_vie/jeu_de_la_vie.htm] |
|||
Il est inventé en 1970 par John Conway ce n'est pas réellement un jeu mais plutôt un automate cellulaire qui est représenté sur une grille (un damier) dont les cellules sont blanches pour l'état mort et noires pour l'état vivant. |
|||
''Extension possible :'' automate d'ulma, automate de la neige extraterrestre. |
|||
[http://therese.eveilleau.pagesperso-orange.fr/pages/truc_mat/textes/conway.htm |
|||
Le but est de faire reproduire, disparaître ou survivre les cellules. Chaque cellule comporte autour d'elles 8 cellules. |
|||
] |
|||
= Jeu de la vie en pratique = |
|||
== Explication plus complète == |
|||
[[Fichier:gg.png]] |
|||
Les règles du jeu de la vie sont plutôt simple. |
|||
Si une cellule a l'état vivant comporte autour d'elle 2 ou 3 cellules vivantes elle survit. |
|||
Si une cellule à l'état vivant comporte aucune,1 ou plus de 3 cellules elle meurt. |
|||
Et si une cellule à l'état mort comporte 3 cellules autour d'elle elle naît. |
|||
== Exemple de configuration == |
|||
Forme stable |
|||
[[Fichier:stable.png]] |
|||
Ce sont des formes qui restent tel quelle, qui n'évoluent pas de génération en génération. |
|||
Oscillation |
|||
[[Fichier:oscillation.png]] |
|||
Ce sont des formes qui redeviennent à l'état initial toutes les 2 générations. |
|||
Il existe beaucoup d'exemples de configuration dont une partie qui intervienne souvent(stable,vaisseau,oscillation) et d'autres très rarement(puffers,canon,jardin d'eden). |
|||
== Extension possible == |
|||
Les extensions du jeu de la vie sont en fait des jeu de la vie avec des règles différentes. |
|||
Une extension du jeu de la vie est l'automate d'Ulam. Pour cette automate contrairement au jeu de la vie les cellules vivantes reste en vie à l'infini. Pour que une cellule naisse elle doit être adjacente orthogonalement (nord, sud, est et ouest) à une et une seule cellule vivante de la génération n précédente. On remarque que l'automate reste figé au bout d'une certaine géneration.. |
|||
Voici un exemple comment l'utiliser et une autre extension possible du jeu de la vie: La neige extraterrestre. |
|||
[http://therese.eveilleau.pagesperso-orange.fr/pages/truc_mat/textes/conway.htm] |
|||
== Implémentation == |
|||
from tkinter import * |
|||
from random import randrange |
|||
def grille(): #fonction dessinant le tableau |
|||
ligne_vert() |
|||
ligne_hor() |
|||
def ligne_vert(): |
|||
c_x = 0 |
|||
while c_x != width: |
|||
can1.create_line(c_x,0,c_x,height,width=1,fill='black') |
|||
c_x+=c |
|||
def ligne_hor(): |
|||
c_y = 0 |
|||
while c_y != height: |
|||
can1.create_line(0,c_y,width,c_y,width=1,fill='black') |
|||
c_y+=c |
|||
def click_gauche(event): #fonction rendant vivante la cellule cliquée donc met la valeur 1 pour la cellule cliquée au dico_case |
|||
x = event.x -(event.x%c) |
|||
y = event.y -(event.y%c) |
|||
can1.create_rectangle(x, y, x+c, y+c, fill='blue') |
|||
dico_case[x,y]=1 |
|||
def click_droit(event): #fonction tuant la cellule cliquée donc met la valeur 0 pour la cellule cliquée au dico_case |
|||
x = event.x -(event.x%c) |
|||
y = event.y -(event.y%c) |
|||
can1.create_rectangle(x, y, x+c, y+c, fill='white') |
|||
dico_case[x,y]=0 |
|||
def canon(): |
|||
dico_case[0*c,5*c]=1 |
|||
dico_case[0*c,6*c]=1 |
|||
dico_case[1*c,5*c]=1 |
|||
dico_case[1*c,6*c]=1 |
|||
dico_case[10*c,5*c]=1 |
|||
dico_case[10*c,6*c]=1 |
|||
dico_case[10*c,7*c]=1 |
|||
dico_case[11*c,4*c]=1 |
|||
dico_case[11*c,8*c]=1 |
|||
dico_case[12*c,3*c]=1 |
|||
dico_case[12*c,9*c]=1 |
|||
dico_case[13*c,3*c]=1 |
|||
dico_case[13*c,9*c]=1 |
|||
dico_case[14*c,6*c]=1 |
|||
dico_case[15*c,4*c]=1 |
|||
dico_case[15*c,8*c]=1 |
|||
dico_case[16*c,5*c]=1 |
|||
dico_case[16*c,6*c]=1 |
|||
dico_case[16*c,7*c]=1 |
|||
dico_case[17*c,6*c]=1 |
|||
dico_case[20*c,3*c]=1 |
|||
dico_case[20*c,4*c]=1 |
|||
dico_case[20*c,5*c]=1 |
|||
dico_case[21*c,3*c]=1 |
|||
dico_case[21*c,4*c]=1 |
|||
dico_case[21*c,5*c]=1 |
|||
dico_case[22*c,2*c]=1 |
|||
dico_case[22*c,6*c]=1 |
|||
dico_case[24*c,1*c]=1 |
|||
dico_case[24*c,2*c]=1 |
|||
dico_case[24*c,6*c]=1 |
|||
dico_case[24*c,7*c]=1 |
|||
dico_case[34*c,3*c]=1 |
|||
dico_case[34*c,4*c]=1 |
|||
dico_case[35*c,3*c]=1 |
|||
dico_case[35*c,4*c]=1 |
|||
demarrer() |
|||
def demarrer(): |
|||
"démarrage de l'animation" |
|||
global flag |
|||
if flag ==0: |
|||
flag =1 |
|||
play() |
|||
def stop(): |
|||
"arrêt de l'animation" |
|||
global flag |
|||
flag =0 |
|||
def play(): #fonction comptant le nombre de cellules vivantes autour de chaque cellule |
|||
global flag, vitesse |
|||
v=0 |
|||
while v!= width/c: |
|||
w=0 |
|||
while w!= height/c: |
|||
x=v*c |
|||
y=w*c |
|||
# les coins |
|||
if x==0 and y==0: #coin en haut à gauche |
|||
compt_viv=0 |
|||
if dico_case[x, y+c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x+c, y]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x+c, y+c]==1: |
|||
compt_viv+=1 |
|||
dico_etat[x, y]=compt_viv |
|||
elif x==0 and y==int(height-c): #coin en bas à gauche |
|||
compt_viv=0 |
|||
if dico_case[x, y-c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x+c, y-c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x+c, y]==1: |
|||
compt_viv+=1 |
|||
dico_etat[x, y]=compt_viv |
|||
elif x==int(width-c) and y==0: #coin en haut à droite |
|||
compt_viv=0 |
|||
if dico_case[x-c, y]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x-c, y+c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x, y+c]==1: |
|||
compt_viv+=1 |
|||
dico_etat[x, y]=compt_viv |
|||
elif x==int(width-c) and y==int(height-c): #coin en bas à droite |
|||
compt_viv=0 |
|||
if dico_case[x-c, y-c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x-c, y]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x, y-c]==1: |
|||
compt_viv+=1 |
|||
dico_etat[x, y]=compt_viv |
|||
# les bords du tableau (sans les coins) |
|||
elif x==0 and 0<y<int(height-c): # bord de gauche |
|||
compt_viv=0 |
|||
if dico_case[x, y-c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x, y+c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x+c, y-c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x+c, y]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x+c, y+c]==1: |
|||
compt_viv+=1 |
|||
dico_etat[x, y]=compt_viv |
|||
elif x==int(width-c) and 0<y<int(height-c): # bord de droite |
|||
compt_viv=0 |
|||
if dico_case[x-c, y-c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x-c, y]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x-c, y+c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x, y-c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x, y+c]==1: |
|||
compt_viv+=1 |
|||
dico_etat[x, y]=compt_viv |
|||
elif 0<x<int(width-c) and y==0: # bord du haut |
|||
compt_viv=0 |
|||
if dico_case[x-c, y]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x-c, y+c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x, y+c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x+c, y]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x+c, y+c]==1: |
|||
compt_viv+=1 |
|||
dico_etat[x, y]=compt_viv |
|||
elif 0<x<int(width-c) and y==int(height-c): # bord du bas |
|||
compt_viv=0 |
|||
if dico_case[x-c, y-c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x-c, y]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x, y-c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x+c, y-c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x+c, y]==1: |
|||
compt_viv+=1 |
|||
dico_etat[x, y]=compt_viv |
|||
#les cellules qui ne sont pas dans les bords du tableau |
|||
else: |
|||
compt_viv=0 |
|||
if dico_case[x-c, y-c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x-c, y]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x-c, y+c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x, y-c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x, y+c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x+c, y-c]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x+c, y]==1: |
|||
compt_viv+=1 |
|||
if dico_case[x+c, y+c]==1: |
|||
compt_viv+=1 |
|||
dico_etat[x, y]=compt_viv |
|||
w+=1 |
|||
v+=1 |
|||
redessiner() |
|||
if flag >0: |
|||
fen1.after(vitesse,play) |
|||
def redessiner(): #fonction redessinant le tableau à partir de dico_etat |
|||
can1.delete(ALL) |
|||
grille() |
|||
t=0 |
|||
while t!= width/c: |
|||
u=0 |
|||
while u!= height/c: |
|||
x=t*c |
|||
y=u*c |
|||
if dico_etat[x,y]==3: |
|||
dico_case[x,y]=1 |
|||
can1.create_rectangle(x, y, x+c, y+c, fill='Blue') |
|||
elif dico_etat[x,y]==2: |
|||
if dico_case[x,y]==1: |
|||
can1.create_rectangle(x, y, x+c, y+c, fill='Blue') |
|||
else: |
|||
can1.create_rectangle(x, y, x+c, y+c, fill='white') |
|||
elif dico_etat[x,y]<2 or dico_etat[x,y]>3: |
|||
dico_case[x,y]=0 |
|||
can1.create_rectangle(x, y, x+c, y+c, fill='white') |
|||
u+=1 |
|||
t+=1 |
|||
#les différentes variables: |
|||
# taille de la grille |
|||
height = 800 |
|||
width = 800 |
|||
#taille des cellules |
|||
c = 10 |
|||
#vitesse de l'animation |
|||
vitesse=50 |
|||
flag=0 |
|||
dico_etat = {} #dictionnaire contenant le nombre de cellules vivantes autour de chaque cellule |
|||
dico_case = {} #dictionnaire contenant les coordonnées de chaques cellules et une valeur 0 ou 1 si elles sont respectivement mortes ou vivantes |
|||
i=0 |
|||
while i!= width/c: #assigne une valeur 0(morte) a chaque coordonnées(cellules) (valeur par défault en quelque sorte ) |
|||
j=0 |
|||
while j!= height/c: |
|||
x=i*c |
|||
y=j*c |
|||
dico_case[x,y]=0 |
|||
j+=1 |
|||
i+=1 |
|||
#programme "principal" |
|||
fen1 = Tk() |
|||
can1 = Canvas(fen1, width =width, height =height, bg ='white') |
|||
can1.bind("<Button-1>", click_gauche) |
|||
can1.bind("<Button-3>", click_droit) |
|||
can1.pack(side =TOP, padx =5, pady =5) |
|||
grille() |
|||
b1 = Button(fen1, text ='Demarrer!', command =demarrer) |
|||
b2 = Button(fen1, text ='Stop', command =stop) |
|||
b1.pack(side =LEFT, padx =3, pady =3) |
|||
b2.pack(side =LEFT, padx =3, pady =3) |
|||
b3 = Button(fen1, text ='Canon planeur', command =canon) |
|||
b3.pack(side =LEFT, padx =3, pady =3) |
|||
b4 = Button(fen1, text ='aléatoire', command =aleatoire) |
|||
b4.pack(side =LEFT, padx =3, pady =3) |
|||
b5= Button(fen1, text ='clear', command =clear) |
|||
b5.pack(side =LEFT, padx =3, pady =3) |
|||
fen1.mainloop() |
|||
A l'aide du jeu de la vie il est possible de réaliser beaucoup de choses comme par exemple additionner 2 nombres cependant cela est plus dur que par exemple avec une machine de Turing. |
|||
Réalisé par Thibault Chaminade étudiant en CMI Info. |
|||
= Source = |
|||
[http://cypris.fr/loisirs/le_jeu_de_la_vie/jeu_de_la_vie.htm] |
|||
[http://zanotti.univ-tln.fr/turing/] |
|||
[http://codes-sources.commentcamarche.net/source/54104-jeu-de-la-vie-simple-et-graphique-tkinter-en-python-3] |
|||
[https://fr.wikipedia.org/wiki/Fonction_calculable] |
|||
[https://fr.wikipedia.org/wiki/Calculabilit%C3%A9] |
|||
Dernière version du 25 mai 2017 à 13:20
Calculabilité pour des fonctions de N → N
Les cours d’informatique peuvent donner l’impression que pour chaque problème on peut trouver un algorithme de solution. Une question fondamentale de l’informatique théorique est de déterminer si un problème donné peut être ou non résolu par d’un ordinateur (par une procédure effective). En particulier se pose la question de déterminer si une fonction donnée peut être calculée au moyen d’un algorithme. La calculabilité qui est une branche de la logique et de l'informatique théorique, permet de définir ce qui est calculable et ce qui ne l’est pas et nous montrera que pour de nombreux problèmes il n’existe pas d’algorithme. La calculabilité nous aide à comprendre les limites de ce que nous pouvons calculer et de ce que nous pouvons faire avec un ordinateur.
Fonction calculable
Une fonction f avec un argument x est calculable s’il existe un algorithme pour calculer f(x) peu importe le nombre d'étapes. Les fonctions calculables sont également appelées fonctions récursives ou fonctions programmables. Nous connaissons de très nombreuses fonctions calculables. En particulier toutes celles que nous avons programmées ! La plupart des fonctions que l'on rencontre en mathématiques le sont :
- somme, différence, produit, égalité, division, puissance…union, intersection, quantification bornée…
- PGCD (algorithme d’Euclide)
-Programmes informatiques qui s'arrêtent.
Fonction non calculable
Une fonction non calculable est donc une fonction pour laquelle aucun programme n’existe. Les deux fonctions non calculables les plus connues sont :
- problème de l'arrêt c’est-à-dire l’exécution interminable d’un programme.
- « Castor affairé » : ce concept a été introduit en 1962 par le mathématicien hongrois Tibor Radó. C’est l'un des premiers exemples connus de fonction non calculable.
Un « castor affairé » est une machine de Turing à n états qui écrit un maximum de « 1 » sur le ruban avant de s’arrêter. Au-delà d’un n trop élevé on ne peut pas déterminer quel est le castor affairé pour un nombre d’états même avec un ordinateur puissant.
Dénombrement de fonction calculable
Il existe une infinité de fonctions, l’ensemble des fonctions n’est donc pas dénombrable. Par contre l’ensemble des programmes, lui, est dénombrable. Il existe donc beaucoup plus de fonctions que de programmes par conséquent il existe un nombre infini de fonctions qui ne sont pas calculables par un programme ce qui revient à dire que la plus grande partie des problèmes que l’on peut définir en mathématiques n’ont pas de solution algorithmique.
Modèles de calcul
Machine de Turing
Ci dessus une machine de Turring réalisé en lego à Lyon.
Cette machine a été inventée par Alan Turing en 1936. Elle va définir la notion de fonction calculable. C’est une machine abstraite et mathématique. On peut exécuter n'importe quel programme que l'on peut exécuter sur un ordinateur, on peut aussi simulé n'importe quel automate fini ou à pile. Une machine de Turing est composée de plusieurs éléments :
- d'une unité de contrôle (registre d'état et table d'action)
- d'un ruban infini divisé en cases
- d'une tête de lecture/ écriture.
L'unité de contrôle permet la mémorisation de l'état courant et dit à la machine dans quel sens se déplacer à la tête de lecture/écriture.
Le ruban joue le rôle de périphérique entrée, sortie. Vierge au début on y inscrit les données que traite le programme.
La tête lecture/écriture lit le contenu de la case sur laquelle elle se trouve elle permet de l'effacer ou écrit un nouveau symbole. Elle peut se déplacer à gauche ou à droite.
A la fin du programme, les mots sur le ruban constituent le résultat final du calcul.
Le fonctionnement dépend de deux paramètres : du symbole lu (c'est la case où se trouve la tête de lecture/écriture) et de l'état de la machine. Ce couple va exécuter ce que demande le programme.
La machine de Turing est un sextuplé (Q, Σ, Γ, δ, q0, F) :
Q est un ensemble fini d’états.
Σ est l’alphabet (fini) d’entrée.
Γ est l’alphabet (fini) du ruban.
δ : Q × Γ → Q × Γ × {G, D, I} est la fonction de transition.
q0 est l’état initial.
F ⊆ Q est l’ensemble des états accepteurs.
Exemple d'utilisation de Turing : [https://interstices.info/jcms/nn_72391/comment-fonctionne-une-machine-de-turing ]
Automate cellulaire
Ci dessus le canon planeur réalisé à l'aide de python.
Un automate cellulaire est un objet mathématique que l'on peut étudier aussi en informatique. Il évolue par étape et selon des règles plus ou moins simples. Il est constitué d'une grille et de plusieurs états, souvent 2 : mort ou en vie.
Cet objet mathématique provient des travaux de John Von Neumann et Stanislaw Ulaw en 1950 qui voulaient comprendre comment se comportait une structure artificielle, c'est à dire comme les êtres vivants. Elles constituent donc aussi un modèle de calcul.
L’automate cellulaire le plus connu est le jeu de la vie. On peut citer également L'automate d'Ullman et l’automate Neige extraterrestre des dérivés du jeu de la vie.
Jeu de la vie
Il est inventé en 1970 par John Conway ce n'est pas réellement un jeu mais plutôt un automate cellulaire qui est représenté sur une grille (un damier) dont les cellules sont blanches pour l'état mort et noires pour l'état vivant.
Le but est de faire reproduire, disparaître ou survivre les cellules. Chaque cellule comporte autour d'elles 8 cellules.
Jeu de la vie en pratique
Explication plus complète
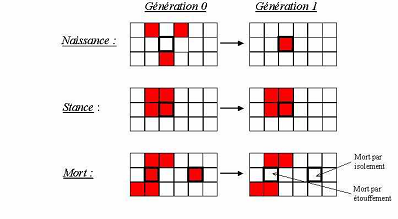
Les règles du jeu de la vie sont plutôt simple.
Si une cellule a l'état vivant comporte autour d'elle 2 ou 3 cellules vivantes elle survit.
Si une cellule à l'état vivant comporte aucune,1 ou plus de 3 cellules elle meurt.
Et si une cellule à l'état mort comporte 3 cellules autour d'elle elle naît.
Exemple de configuration
Forme stable
Ce sont des formes qui restent tel quelle, qui n'évoluent pas de génération en génération.
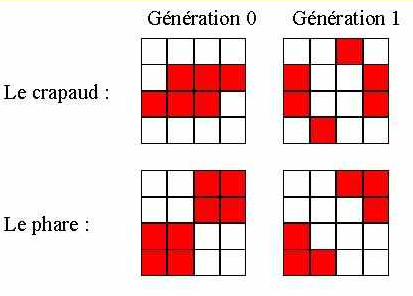
Oscillation
Ce sont des formes qui redeviennent à l'état initial toutes les 2 générations.
Il existe beaucoup d'exemples de configuration dont une partie qui intervienne souvent(stable,vaisseau,oscillation) et d'autres très rarement(puffers,canon,jardin d'eden).
Extension possible
Les extensions du jeu de la vie sont en fait des jeu de la vie avec des règles différentes.
Une extension du jeu de la vie est l'automate d'Ulam. Pour cette automate contrairement au jeu de la vie les cellules vivantes reste en vie à l'infini. Pour que une cellule naisse elle doit être adjacente orthogonalement (nord, sud, est et ouest) à une et une seule cellule vivante de la génération n précédente. On remarque que l'automate reste figé au bout d'une certaine géneration..
Voici un exemple comment l'utiliser et une autre extension possible du jeu de la vie: La neige extraterrestre. [1]
Implémentation
from tkinter import * from random import randrange
def grille(): #fonction dessinant le tableau
ligne_vert()
ligne_hor()
def ligne_vert():
c_x = 0
while c_x != width:
can1.create_line(c_x,0,c_x,height,width=1,fill='black')
c_x+=c
def ligne_hor():
c_y = 0
while c_y != height:
can1.create_line(0,c_y,width,c_y,width=1,fill='black')
c_y+=c
def click_gauche(event): #fonction rendant vivante la cellule cliquée donc met la valeur 1 pour la cellule cliquée au dico_case
x = event.x -(event.x%c) y = event.y -(event.y%c) can1.create_rectangle(x, y, x+c, y+c, fill='blue') dico_case[x,y]=1
def click_droit(event): #fonction tuant la cellule cliquée donc met la valeur 0 pour la cellule cliquée au dico_case
x = event.x -(event.x%c) y = event.y -(event.y%c) can1.create_rectangle(x, y, x+c, y+c, fill='white') dico_case[x,y]=0
def canon():
dico_case[0*c,5*c]=1 dico_case[0*c,6*c]=1 dico_case[1*c,5*c]=1 dico_case[1*c,6*c]=1 dico_case[10*c,5*c]=1 dico_case[10*c,6*c]=1 dico_case[10*c,7*c]=1 dico_case[11*c,4*c]=1 dico_case[11*c,8*c]=1 dico_case[12*c,3*c]=1 dico_case[12*c,9*c]=1 dico_case[13*c,3*c]=1 dico_case[13*c,9*c]=1 dico_case[14*c,6*c]=1 dico_case[15*c,4*c]=1 dico_case[15*c,8*c]=1 dico_case[16*c,5*c]=1 dico_case[16*c,6*c]=1 dico_case[16*c,7*c]=1 dico_case[17*c,6*c]=1 dico_case[20*c,3*c]=1 dico_case[20*c,4*c]=1 dico_case[20*c,5*c]=1 dico_case[21*c,3*c]=1 dico_case[21*c,4*c]=1 dico_case[21*c,5*c]=1 dico_case[22*c,2*c]=1 dico_case[22*c,6*c]=1 dico_case[24*c,1*c]=1 dico_case[24*c,2*c]=1 dico_case[24*c,6*c]=1 dico_case[24*c,7*c]=1 dico_case[34*c,3*c]=1 dico_case[34*c,4*c]=1 dico_case[35*c,3*c]=1 dico_case[35*c,4*c]=1 demarrer()
def demarrer():
"démarrage de l'animation"
global flag
if flag ==0:
flag =1
play()
def stop():
"arrêt de l'animation" global flag flag =0
def play(): #fonction comptant le nombre de cellules vivantes autour de chaque cellule
global flag, vitesse
v=0
while v!= width/c:
w=0
while w!= height/c:
x=v*c
y=w*c
# les coins
if x==0 and y==0: #coin en haut à gauche
compt_viv=0
if dico_case[x, y+c]==1:
compt_viv+=1
if dico_case[x+c, y]==1:
compt_viv+=1
if dico_case[x+c, y+c]==1:
compt_viv+=1
dico_etat[x, y]=compt_viv
elif x==0 and y==int(height-c): #coin en bas à gauche
compt_viv=0
if dico_case[x, y-c]==1:
compt_viv+=1
if dico_case[x+c, y-c]==1:
compt_viv+=1
if dico_case[x+c, y]==1:
compt_viv+=1
dico_etat[x, y]=compt_viv
elif x==int(width-c) and y==0: #coin en haut à droite
compt_viv=0
if dico_case[x-c, y]==1:
compt_viv+=1
if dico_case[x-c, y+c]==1:
compt_viv+=1
if dico_case[x, y+c]==1:
compt_viv+=1
dico_etat[x, y]=compt_viv
elif x==int(width-c) and y==int(height-c): #coin en bas à droite
compt_viv=0
if dico_case[x-c, y-c]==1:
compt_viv+=1
if dico_case[x-c, y]==1:
compt_viv+=1
if dico_case[x, y-c]==1:
compt_viv+=1
dico_etat[x, y]=compt_viv
# les bords du tableau (sans les coins)
elif x==0 and 0<y<int(height-c): # bord de gauche
compt_viv=0
if dico_case[x, y-c]==1:
compt_viv+=1
if dico_case[x, y+c]==1:
compt_viv+=1
if dico_case[x+c, y-c]==1:
compt_viv+=1
if dico_case[x+c, y]==1:
compt_viv+=1
if dico_case[x+c, y+c]==1:
compt_viv+=1
dico_etat[x, y]=compt_viv
elif x==int(width-c) and 0<y<int(height-c): # bord de droite
compt_viv=0
if dico_case[x-c, y-c]==1:
compt_viv+=1
if dico_case[x-c, y]==1:
compt_viv+=1
if dico_case[x-c, y+c]==1:
compt_viv+=1
if dico_case[x, y-c]==1:
compt_viv+=1
if dico_case[x, y+c]==1:
compt_viv+=1
dico_etat[x, y]=compt_viv
elif 0<x<int(width-c) and y==0: # bord du haut
compt_viv=0
if dico_case[x-c, y]==1:
compt_viv+=1
if dico_case[x-c, y+c]==1:
compt_viv+=1
if dico_case[x, y+c]==1:
compt_viv+=1
if dico_case[x+c, y]==1:
compt_viv+=1
if dico_case[x+c, y+c]==1:
compt_viv+=1
dico_etat[x, y]=compt_viv
elif 0<x<int(width-c) and y==int(height-c): # bord du bas
compt_viv=0
if dico_case[x-c, y-c]==1:
compt_viv+=1
if dico_case[x-c, y]==1:
compt_viv+=1
if dico_case[x, y-c]==1:
compt_viv+=1
if dico_case[x+c, y-c]==1:
compt_viv+=1
if dico_case[x+c, y]==1:
compt_viv+=1
dico_etat[x, y]=compt_viv
#les cellules qui ne sont pas dans les bords du tableau
else:
compt_viv=0
if dico_case[x-c, y-c]==1:
compt_viv+=1
if dico_case[x-c, y]==1:
compt_viv+=1
if dico_case[x-c, y+c]==1:
compt_viv+=1
if dico_case[x, y-c]==1:
compt_viv+=1
if dico_case[x, y+c]==1:
compt_viv+=1
if dico_case[x+c, y-c]==1:
compt_viv+=1
if dico_case[x+c, y]==1:
compt_viv+=1
if dico_case[x+c, y+c]==1:
compt_viv+=1
dico_etat[x, y]=compt_viv
w+=1
v+=1
redessiner()
if flag >0:
fen1.after(vitesse,play)
def redessiner(): #fonction redessinant le tableau à partir de dico_etat
can1.delete(ALL)
grille()
t=0
while t!= width/c:
u=0
while u!= height/c:
x=t*c
y=u*c
if dico_etat[x,y]==3:
dico_case[x,y]=1
can1.create_rectangle(x, y, x+c, y+c, fill='Blue')
elif dico_etat[x,y]==2:
if dico_case[x,y]==1:
can1.create_rectangle(x, y, x+c, y+c, fill='Blue')
else:
can1.create_rectangle(x, y, x+c, y+c, fill='white')
elif dico_etat[x,y]<2 or dico_etat[x,y]>3:
dico_case[x,y]=0
can1.create_rectangle(x, y, x+c, y+c, fill='white')
u+=1
t+=1
- les différentes variables:
- taille de la grille
height = 800 width = 800
- taille des cellules
c = 10
- vitesse de l'animation
vitesse=50
flag=0 dico_etat = {} #dictionnaire contenant le nombre de cellules vivantes autour de chaque cellule
dico_case = {} #dictionnaire contenant les coordonnées de chaques cellules et une valeur 0 ou 1 si elles sont respectivement mortes ou vivantes i=0 while i!= width/c: #assigne une valeur 0(morte) a chaque coordonnées(cellules) (valeur par défault en quelque sorte )
j=0
while j!= height/c:
x=i*c
y=j*c
dico_case[x,y]=0
j+=1
i+=1
- programme "principal"
fen1 = Tk()
can1 = Canvas(fen1, width =width, height =height, bg ='white') can1.bind("<Button-1>", click_gauche) can1.bind("<Button-3>", click_droit) can1.pack(side =TOP, padx =5, pady =5)
grille()
b1 = Button(fen1, text ='Demarrer!', command =demarrer)
b2 = Button(fen1, text ='Stop', command =stop)
b1.pack(side =LEFT, padx =3, pady =3) b2.pack(side =LEFT, padx =3, pady =3)
b3 = Button(fen1, text ='Canon planeur', command =canon) b3.pack(side =LEFT, padx =3, pady =3)
b4 = Button(fen1, text ='aléatoire', command =aleatoire) b4.pack(side =LEFT, padx =3, pady =3)
b5= Button(fen1, text ='clear', command =clear) b5.pack(side =LEFT, padx =3, pady =3)
fen1.mainloop()
A l'aide du jeu de la vie il est possible de réaliser beaucoup de choses comme par exemple additionner 2 nombres cependant cela est plus dur que par exemple avec une machine de Turing.
Réalisé par Thibault Chaminade étudiant en CMI Info.