« VISI201 CMI : visite de laboratoire » : différence entre les versions

De Wiki du LAMA (UMR 5127)
Aller à la navigation Aller à la recherche
Ligne 133 : Ligne 133 :


==[[Complexité pratique contre complexité théorique]]==
==[[Complexité pratique contre complexité théorique]]==

* Tuteur : Pierre Hyvernat

* Résumé : la complexité ''théorique'' d'un algorithme est une estimation du nombre d'opérations élémentaires nécessaires pour que l'algorithme termine, en fonction de ses arguments. On ne peut pas donner de réponse exacte, et cette complexité prend typiquement la forme : "le nombre d'opérations élémentaires pour trouver le minimum d'un tableau (avec l'algorithme standard) est proportionnel à la taille du tableau". La complexité ''pratique'' d'un programme est simplement le temps qu'il met sur certains arguments. Par exemple "mon programme du tri bulle prend 4 secondes sur un tableau de taille 10000".<br /> Normalement, une meilleur complexité théorique se traduit par une meilleur complexité pratique, mais ce n'est pas toujours le cas. Nous allons implémenter et comparer plusieurs programmes et étudier la différence entre ces deux notions de complexité. Python sera le langage initial, mais suivant l'étudiant, d'autres langages plus bas niveau pourront être utilisés.

* Objectif :
*# comprendre la définition de complexité théorique
*# implémenter des algorithmes pour le même problème et comparer les complexités pratiques et théoriques, comme par exemple
*#* multiplication naive / méthode de Karatsuba / méthode de Toom-Cook
*#* recherche de la mediane naive / méthode quickselect / méthode linéaire
*#* tri par insertion / tri rapide / tri fusion
*# expliquer d'où peuvent venir les différences constatées, et chercher comment améliorer la complexité "pratique" des programmes correspondants.

* quelques liens :
** multiplication de Karatsuba : http://gersoo.free.fr/Download/docs/kar.pdf
** recherche de la médiane linéaire : https://fr.wikipedia.org/wiki/M%C3%A9diane_des_m%C3%A9dianes
** algorithme quickselect : https://fr.wikipedia.org/wiki/Quickselect


== [[Etude du protocole gRPC]] ==
== [[Etude du protocole gRPC]] ==

Version du 16 octobre 2020 à 07:38

  • Cours du semestre 2 du parcours CMI Informatique (licence INFO).
  • Responsable pour 2020--2021: Jacques-Olivier Lachaud
  • Responsable pour 2019--2020: Jacques-Olivier Lachaud
  • Responsable pour 2018--2019: Jacques-Olivier Lachaud
  • Responsable pour 2017--2018: Jacques-Olivier Lachaud
  • Responsable pour 2016--2017: Jacques-Olivier Lachaud

Descriptif

L'objectif du module est de faire découvrir les laboratoires, le monde de la recherche et les enseignants-chercheurs et chercheurs, ainsi que la réflexion scientifique. Cela se fait de deux manières.

D'abord, une partie de ce module consiste à assister à des séminaires dédiés aux étudiants CMI Informatique et Mathématique (1 fois par mois, les jeudi après-midi). [Planning des séminaires CMI]

Ces séminaires "grand public" portent sur des sujets variées en informatique et mathématiques.

Les étudiants choisissent ensuite d'approfondir un sujet proposé par les enseignants, ou un sujet motivé de leur choix (en accord avec le responsable du module). Ce travail se fait en interaction avec un tuteur académique (5-6 contacts au moins). Ce travail personnel tuteuré donne lieu à la rédaction d'une synthèse sur le sujet sous forme d'une page wiki/web, ainsi que d'un mini-exposé.

Sujets proposés (2020-2021)

(work in progress)

  • Transformée en distance discrète, diagramme de Voronoi discret, axe médian et squelette
  • Clustering par K-means, segmentation d'image
  • Base de données orientées Graphe, similarité et modèles prédictifs
  • Algorithmes d'approximation numérique de la mesure de Mahler
  • Ensemble de Mandelbrot et autres fractales
  • Etude du protocole gRPC

Transformée en distance discrète, diagramme de Voronoi discret, axe médian et squelette

  • Tuteur: Jacques-Olivier Lachaud
  • Résumé: La transformée en distance permet de situer l'éloignement de tout point du plan ou de l'espace à un ensemble donné. C'est un outil de base dans beaucoup d'algorithmes de traitement d'image ou de données 3D. Pour les images, on peut l'utiliser pour filtrer des objets, comparer deux objets, extraire son squelette, mettre en correspondance deux objets. Dans le cas de nuage de points 3D acquis par laser, on peut utiliser cet outil pour reconstruire une surface approchant ces points. Dans ce travail, on se concentrera sur la transformée en distance dans le cas des images 2D (appelé cas discret). Les objets traités seront des ensembles de pixels, par exemple des caractères écrits si on fait de l'analyse de texte scanné. On s'intéressera aux algorithmes spécifiques à ce contexte, ainsi qu'à quelques applications.
  • Objectifs:
    1. Comprendre ce qu'est une distance, une transformée en distance, et un diagramme de Voronoi. Comprendre ce qu'est la stabilité d'une fonction.
    2. Identifier le lien avec l'axe médian et les squelettes
    3. Coder un algorithme de calcul de la transformée en distance et du diagramme de Voronoi dans le cas des images 2D, ainsi que l'extraction de l'axe médian discret.
    4. Si le temps le permet, on s'intéressera aussi à l'extraction d'un squelette "topologique", qui contient l'axe médian discret.
Pixels en entrée Transformée en distance Diagramme de Voronoi Squelette topologique
Dt-input.png Dt-output.png Dt-voronoi.png Skel.png

Base de données orientées Graphe, similarité et modèles prédictifs

  • Tuteur : Gérald Cavallini
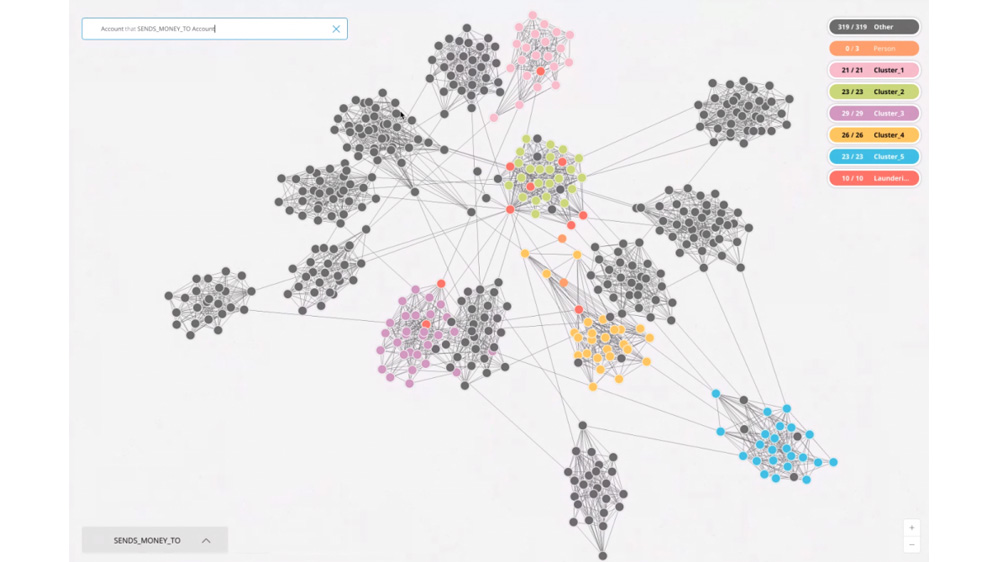
  • Résumé : Avec l’avènement du BigDatas, dans bien des cas le choix d’un produit, d’un média, d’un voyage ... ne peut plus être direct. Il s’appuie sur des systèmes de recommandations. L’importance financière de ces systèmes est énorme Amazon estime à 30% les ventes supplémentaires dues à son système de recommandation. Ces systèmes s’appuient sur des calculs statistiques et des algorithmes de recherche de similarité. Ces algorithmes expriment la distance entre des objets, ce qui permet par exemple d’identifier des utilisateurs(consommateurs, électeur ...) similaire et de recommander leurs choix.
  • Objectifs :
    1. Mettre en œuvre différents algorithmes de recherche de similarité ( similarité de Jaquard, similarité cosinus...) dans une base de donnée orientées Graphe Neo4j.
    2. Proposer un système de recommandation de film à partir de la base MovieLens (Notation de films par des utilisateurs).
    3. Proposer un une validation du modèle prédictif.
  • Liens pour commencer

Neo4j.jpg

Clustering par K-means, segmentation d'image

  • Tuteur: Jacques-Olivier Lachaud
  • Résumé: Le partitionnement de données (ou data clustering) est l'opération visant à découper un ensemble de données en des groupes disjoints, tel que chaque groupe est le plus homogène possible. C'est un procédé à la base de nombreux algorithmes d'analyse de données, et reste encore une tâche difficile, avec de nombreuses définitions possibles. Nous nous intéresserons ici à une méthode standard, relativement simple à mettre en oeuvre, et qui permet de découper un ensemble de données en K groupes, où K est donné. on l'appelle K-means ou algorithme des K-moyennes. Elle opère sur des données où nous pouvons calculer une distance entre toute paire de données. On appliquera cet algorithme aux images couleurs. On verra qu'on peut l'utiliser pour réduire considérablement le nombre de couleurs d'une image tout en la préservant au maximum. On verra aussi, en modifiant la distance, comment utiliser cet algorithme pour faire de la segmentation d'image, c'est-à-dire décomposer une image en ses régions homogènes afin d'identifier les objets d'intérêt.
  • Objectifs:
    1. Comprendre l'algorithme des k-moyennes et comment l'appliquer à l'analyse d'images couleurs
    2. Implémenter cet algorithme avec Python/numpy
    3. Tester les distances entre couleurs, et les distances couleur+géométrie
    4. Montrer son intérêt sur différentes images, ainsi que ses limites
  • Liens pour démarrer
Image en entrée Clustering K=256 Clustering K=10 Spatial clustering K=10, c=0.5
Kowloon-small.png Kowloon-k256.png Kowloon-k10.png Kowloon-k10-s0 5.png

Algorithmes d'approximation numérique de la mesure de Mahler

  • Tuteur : Denys DUTYKH (CR CNRS, Denys.Dutykh@univ-smb.fr)
  • Résumé : Le LAboratoire de MAthématiques (LAMA UMR 5127) de l'USMB se distingue par la grande diversité des recherches menées au sein de cette unité ainsi que par des synergies, parfois surprenantes et inattendues, qui existent entre ses membres. Le présent projet s'inscrit parfaitement dans cette optique. Notamment, nous avons une chance au LAMA d'avoir parmi nous un expert international sur la conjecture de Lehmer et qui se trouve involontairement à l'origine du sujet décrit ci-dessous. Plus précisément, la conjecture de Lehmer porte sur certaines propriétés de l'ensemble de toutes les mesures de Mahler des polynômes univariés à coefficients entiers. La résolution de cette conjecture ne figure pas parmi les objectifs premiers de ce stage même si une telle finalité serait très bien vue par l'encadrant. Dans le premier temps nous allons plutôt étudier et comparer les différentes approches numériques qui existent pour le calcul de la mesure de Mahler d'un polynôme (éventuellement de très grand degré) donné. Si le temps le permet, nous pouvons nous intéresser aussi au calcul de la mesure de Mahler pour des polynômes multivariés bien que cette tâche ait un niveau de difficulté bien supérieur. En cas de difficultés imprévues, nous pourrons ponctuellement consulter l'expert local sur la question qui est toujours très généreux pour partager ses connaissances pointues sur le sujet. Enfin, un certain goût mathématique et une passion (même si elle est dormante) pour la théorie des nombres sont absolument nécessaires pour savourer pleinement le travail sur la mesure de Mahler.
  • Liens pour démarrer
    1. https://mathworld.wolfram.com/LehmersMahlerMeasureProblem.html
    2. https://en.wikipedia.org/wiki/Mahler_measure

Mahler-1.gif Mahler-2.gif


Ensemble de Mandelbrot et autres fractales

  • Tuteur : Pierre Hyvernat
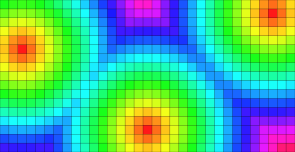
  • Résumé : l'ensemble de Mandelbrot est un sous-ensemble des points du plan avec une structure extrêmement complexe. Comme de nombreuses fractales, cet ensemble donne naissance à des visuels surprenants tels que
    Mandelbrot.jpg
    La couleur d'un point c du plan dépend uniquement de la vitesse à laquelle l'itération de la fonction z -> z*z + c diverge et il est donc facile d'écrire un programme qui dessine (une approximation de) l'ensemble de Mandelbrot. Écrire un programme efficace est un peu plus complexe, et ce encore plus dans des langages comme Python !
  • Objectifs :
    1. écrire une version "naïve" du programme en Python pur,
    2. écrire une seconde version du programme en utilisant des bibliothèques de calcul comme numpy afin de comparer les vitesse d'execution,
    3. appliquer certaines optimisation et étudier lors impact sur le temps de calcul,
    4. à des niveaux de zoom extremes, la précision des nombres flottants n'est plus suffisante. Il peut être intéressant de tester un calcul beaucoup plus lent, mais avec une précision supérieure,
    5. étendre ces programmes pour dessiner les ensembles de julia correspondant à un point du plan.


Complexité pratique contre complexité théorique

  • Tuteur : Pierre Hyvernat
  • Résumé : la complexité théorique d'un algorithme est une estimation du nombre d'opérations élémentaires nécessaires pour que l'algorithme termine, en fonction de ses arguments. On ne peut pas donner de réponse exacte, et cette complexité prend typiquement la forme : "le nombre d'opérations élémentaires pour trouver le minimum d'un tableau (avec l'algorithme standard) est proportionnel à la taille du tableau". La complexité pratique d'un programme est simplement le temps qu'il met sur certains arguments. Par exemple "mon programme du tri bulle prend 4 secondes sur un tableau de taille 10000".
    Normalement, une meilleur complexité théorique se traduit par une meilleur complexité pratique, mais ce n'est pas toujours le cas. Nous allons implémenter et comparer plusieurs programmes et étudier la différence entre ces deux notions de complexité. Python sera le langage initial, mais suivant l'étudiant, d'autres langages plus bas niveau pourront être utilisés.
  • Objectif :
    1. comprendre la définition de complexité théorique
    2. implémenter des algorithmes pour le même problème et comparer les complexités pratiques et théoriques, comme par exemple
      • multiplication naive / méthode de Karatsuba / méthode de Toom-Cook
      • recherche de la mediane naive / méthode quickselect / méthode linéaire
      • tri par insertion / tri rapide / tri fusion
    3. expliquer d'où peuvent venir les différences constatées, et chercher comment améliorer la complexité "pratique" des programmes correspondants.

Etude du protocole gRPC

  • Tuteur : David Télisson
  • Résumé : « gRPC est un framework RPC (Remote procedure call) open source initialement développé par Google. Il utilise le protocole HTTP/2 pour le transport, Protocol Buffers comme langage de description d'interface (IDL : interface description language), et offre des fonctionnalités telles que l'authentification, la transmission bidirectionnelle et le contrôle de flux, par le blocage ou non des communications par annulation ou délais d'attente. Il permet la construction de liaisons client/serveur multiplateforme pour de nombreux langages » [source wikipedia]
  • Objectifs du projet :
    1. Etudier et comprendre ce protocole
    2. Comparer avec les protocoles RPC historiques : XML-RPC ou JSON-RPC
    3. Implémentez un PoC (preuve de concept) simple qui montre le fonctionnement du protocole entre deux applications développées dans des langages différents (Python et JavaScript).
  • Liens pour démarrer :

Sujets réalisés (2019-2020)

Sujets proposés (2019-2020)

  • Compression et transformée de Burrow-Wheeler
  • Backtracking
  • Transfert de couleur (version 2)
  • Génération fractale de terrains
  • Architectures Orientées Micro-Services
  • Apprentissage automatique
  • Algorithmes probabilistes/déterministes pour tester la primalité d'un entier
  • Base de données orientées Graphe, similarité et modèles prédictifs

Compression et transformée de Burrow-Wheeler (lien : Transformée Burrows Wheeler)

  • Tuteur : Pierre Hyvernat
  • Résumé : La transformée de Burrow-Wheeler est l'étape clé de l'algorithme de compression bzip2. C'est une transformation de texte (suite d'octet) qui ne modifie pas la taille, mais ajoute suffisamment de motifs redondants pour améliorer un autre algorithme de compression (algorithme de Huffman dans le cas de bzip2)
  • Objectif : L'objectif est de comprendre le fonctionnement de cette transformation (et de son inverse) et d'implémenter une version naïve de l'algorithme de compression / décompression et de tester sur quelques exemples. Les améliorations de l'algorithme seront ensuite abordées.
  • Liens : Burrows, Michael; Wheeler, David J. (1994), A block sorting lossless data compression algorithm, Technical Report 124, Digital Equipment Corporation [PDF]

Backtracking (lien : VISI201 Backtracking (PICHENOT Simon))

  • Tuteur : Pierre Hyvernat
  • Résumé et objectif : La notion de "backtracking" est fondamentale en algorithmique : il s'agit essentiellement de tester des solutions partielles à un problème, en revenant en arrière dès qu'une incohérence est découverte. Le point de départ sera le fascicule 4.5b de D. Knuth "Introduction to backtracking" et permettra de se familiariser avec les concepts, la terminology et des exemples, qu'il faudra implémenter. Une suite possible sera la notion de réduction de problèmes et l'algorithme-X qui permet de "factoriser" de nombreux problèmes de backtracking en un seul algorithme.
  • Liens : D. Knuth, "the art of computer programming introduction to backtracking" [PS]

Transfert de couleur (version 2)

  • Tuteur: Jacques-Olivier Lachaud
  • Résumé: Le transfert de couleurs de l'image Y vers l'image X consiste à repeindre "au mieux" l'image X avec la palette de couleurs de l'image Y. L'image repeinte X' a alors les mêmes couleurs que l'image Y (mais les pixels ne sont pas répartis pareils). Voir l'exemple de transfert ci-dessous. Il existe plusieurs techniques de transfert de couleurs, mais nous étudierons une technique basée sur le transport optimal. Comme c'est un problème assez difficile dans le cas général, nous étudierons une variante dite par coupe 1D, qui simplifiera considérablement le problème de transport.
Transfert de couleur
Input Output
Horseshoe.jpg Horseshoe-fjord-n40.jpg
Fjord.jpg Fjord-horseshoe-n40.jpg
  • Objectifs:
    1. Comprendre la version 1 fait par [Lucas Chardonnet], comprendre les qualités et limites de l'approche (sur quelle type d'image ça marche assez bien par exemple)
    2. Adapter l'algorithme pour qu'il puisse traiter des images de tailles différentes
    3. Réécrire le code en utilisant la bibliothèque python NUMPY pour accélérer les calculs
    4. Changer les espaces de couleurs utilisés: RGB ne convient pas très bien pour mesurer le coût du transport. Transformer le code pour qu'il puisse utiliser plutôt l'espace [L*a*b*] mieux adapté pour calculer des distances entre couleurs.
  • Liens:

Génération fractale de terrains

  • Tuteur: Jacques-Olivier Lachaud
  • Résumé: La génération procédurale de terrain est très utilisée en modélisation 3D et dans les jeux vidéos, afin de générer rapidement des paysages pseudo-réalistes que l'on étoffera ensuite de façon plus manuelle. On propose d'étudier et d'implémenter un algorithme classique, dit "algorithme Diamant-Carré". Cet algorithme récursif permet de générer une carte d'élévation. Selon les paramètres données, le résultat peut ressembler aux cartes d'altitude de haute montagne ou des collines plus douces.
Génération fractale de terrain par algorithme diamand carré
Elévations générées Colorisation Visualisation 3D
Diamond-Square texture.png Diamond-Square heightmap.png Terragen.jpg
  • Objectifs:
    1. Comprendre et implémenter l'algorithme Diamant-Carré
    2. Comprendre comment paramétrer cet algorithme pour qu'il génère des montagnes bien abrupte à haute altitude ou des collines à basse altitude.
    3. Fabriquer une image de couleur/texture qui va associer des couleurs aux altitudes générées (e.g. forcer du bleu sous l'altitude zero, ajouter de la neige, des lacs, de la forêt)
    4. Générer un fichier 3D (par exemple OBJ) à partir de ces deux images (l'image des hauteurs et l'image des couleurs) pour pouvoir faire de beau rendu 3D (sous blender par exemple)
  • Liens:

Architectures Orientées Micro-Services

  • Tuteur : David Télisson
  • Résumé : Les architectures des applications logicielles distribuées de grandes envergures ont évolué à partir du début des années 2000, d’une application molithique déployée sur un serveur d’application (JEE, TomCat, etc.) vers des solutions fortement répartis déployées sous formes de services. On parle alors d’architectures orientées services qui se traduisent par le développement et le déploiement de services logiciels interrogeables via des protocoles dédiés (par exemple SOAP) et des API (REST). Cette tendance, corrélée aux nouvelles méthodes de management des projets informatiques (méthodes agiles, intégration continue, DevOps1), s’est accentué ces dernières années et a fait émergé un « nouveau » paradigme : le micro-service. Plusieurs aspects caractérisent un micro-service :
    • fonctionnalité unique
    • flexibilité technologie
    • équipe de développement réduite
    • déploiement ciblé
    • support de la montée en charge (scalabilité)
    • tests facilités et intégrés au processus de développement (TDD2)
  • Objectifs du projet :
    1. Etudier et comprendre les concepts liés aux micro-services (API, conteneurisation, framework, etc.)
    2. Implémentez un PoC (proof of concept) qui démontre qu’une application peut se construire dynamiquement par agrégation de micro-services développés avec des langages différents (Python, JS et Java), déployés sur des plateformes différentes (Django, Node et Glassfish) et disponibles sous formes de conteneurs dans le cloud (Azure)
    3. Livrable attendu : un tutoriel « à la OpenClassRooms »
  • Liens pour démarrer :


Apprentissage automatique


Algorithmes probabilistes/déterministes pour tester la primalité d'un entier

  • Tuteur : Sébastien Tavenas
  • Pouvoir tester si un entier est un nombre premier semble être une brique de base si l'on souhaite faire de l'arithmétique sur un ordinateur. Le crible d'Érathostène enseigné dans les petites classes se montre beaucoup trop lent en pratique. L'algorithme probabiliste utilisé le plus rapide est le test de Fermat. Or, si on regarde les algorithmes des librairies "génériques", on peut s'apercevoir que la fonction 'mpz_probab_prime_p' de la librairie 'gmp' sur c++ utilise un test probabiliste de Miller-Rabin, la fonction 'isPrime' de la classe 'Prime' dans java utilise aussi un test de Miller-Rabin mais qui est déterminisé, alors que la fonction 'isprime' de la librairie 'sympy' dans python effectue un test de Miller-Rabin si l'entier est plus petit que 2^64 et un test BPSW fort si l'entier est plus grand. Ainsi, une fonction déjà implémentée de test de primalité peut se tromper ou non, être instantanée ou moins. Que dire alors de l'algorithme polynomial déterministe et toujours correct proposé par AKS?
  • Objectifs :
    1. Comprendre quelques tests de primalité et comment l'aléatoire est utilisé dans ces algorithmes
    2. Comprendre la notion de nombre pseudopremier qui explique, entre autre, quand il vaut mieux utiliser le test de Fermat ou celui de Miller-Rabin
    3. Programmer quelques uns des ces tests et les comparer
    4. Essayer de dérandomiser ces tests à l'aide de hitting-sets précalculés


Base de données orientées Graphe, similarité et modèles prédictifs

  • Tuteur : Gérald Cavallini
  • Résumé : Avec l’avènement du BigDatas, dans bien des cas le choix d’un produit, d’un média, d’un voyage ... ne peut plus être direct. Il s’appuie sur des systèmes de recommandations. L’importance financière de ces systèmes est énorme Amazon estime à 30% les ventes supplémentaires dues à son système de recommandation. Ces systèmes s’appuient sur des calculs statistiques et des algorithmes de recherche de similarité. Ces algorithmes expriment la distance entre des objets, ce qui permet par exemple d’identifier des utilisateurs(consommateurs, électeur ...) similaire et de recommander leurs choix.
  • Objectifs :
    1. Mettre en œuvre différents algorithmes de recherche de similarité ( similarité de Jaquard, similarité cosinus...) dans une base de donnée orientées Graphe Neo4j.
    2. Proposer un système de recommandation de film à partir de la base MovieLens (Notation de films par des utilisateurs).
    3. Proposer un une validation du modèle prédictif.
  • Liens pour commencer

Neo4j.jpg

Sujets réalisés (2018-2019)

Sujets proposés (2018-2019)

  • Transport optimal par coupe 1D et transfert de couleurs entre images
  • Génération et résolution de labyrinthes II
  • REST + Pub/Sub : protocole hybride pour l’IoT
  • La suite de Conway et la classification périodique des "éléments"
  • Initiation à la démonstration sur ordinateur et certification de logiciel
  • Algorithmes probabilistes/déterministes pour tester la primalité d'un entier
  • Dilemme du prisonnier

Transport optimal par coupe 1D et transfert de couleurs entre images

  • Tuteur: Jacques-Olivier Lachaud
  • Résumé: Le transfert de couleurs de l'image Y vers l'image X consiste à repeindre "au mieux" l'image X avec la palette de couleurs de l'image Y. L'image repeinte X' a alors les mêmes couleurs que l'image Y (mais les pixels ne sont pas répartis pareils). Voir l'exemple de transfert ci-dessous. Il existe plusieurs techniques de transfert de couleurs, mais nous étudierons une technique basée sur le transport optimal. Comme c'est un problème assez difficile dans le cas général, nous verrons une variante dite par coupe 1D, qui simplifiera considérablement le problème de transport.

Ex-transfert-couleur-OT.png

  • Objectifs:
    1. comprendre ce qu'est une image niveaux couleur, et ce qu'on appelle le transfert de couleurs.
    2. comprendre le principe du transport optimal (discret).
    3. comprendre et décrire le principe du transport optimal par coupe 1D, et comment se fait le calcul du meilleur transport dans ce cas.
    4. Coder un programme de transfert de couleur, qui prend deux images couleurs et réalise le transfert de couleurs.
    5. On pourra ensuite réfléchir à quelques améliorations simples (espace couleur YUV, grouper les pixels).
  • Liens pour démarrer
    • Le vrai "Transport Optimal" est vite très mathématique (ce sont des mesures qui sont transportées), mais on peut l'aborder beaucoup plus simplement dans le cas discret (un nombre fini de valeurs) comme une simple assignation entre deux ensembles.
    • [Transfert de couleur Wikipedia]
    • [Habilitation de N. Papadakis] (regardez les images plutôt).

Génération et résolution de labyrinthes II

  • Tuteur: François Boussion
  • Résumé: On veut générer des labyrinthes aussi grands et complexes que possible, avec des murs dans une grille carré voire d'autres domaines. Comment faire pour qu'il y ait toujours un chemin de l'entrée à la sortie ? Comment faire pour qu'il n'y ait qu'un chemin ? Ensuite, comment trouver la sortie quand on est perdu dans le labyrinthe.
  • Objectifs:
    1. Comprendre comment représenter un labyrinthe avec une structure de données simple
    2. Voir le lien avec la théorie des graphes et voir que le problème se résout de la même façon pour des grilles carrées, hexagonales ou autres.
    3. Comprendre l'algorithme d'arbre couvrant minimum
    4. Comprendre le principe du parcours en profondeur et de la récursivité
  • Pour aller plus loin
    1. coder la génération d'un labyrinthe et sa visualisation
    2. introduire des poids pour varier le labyrinthe
    3. comment faire un labyrinthe sur grille hexagonale avec des tableaux.
  • Liens pour démarrer

REST + Pub/Sub : protocole hybride pour l’IoT

  • Tuteur: David Télisson
  • Résumé: L’avènement de l’Internet des Objets (IoT) depuis une dizaine d’années a fait apparaitre des problématiques propres aux protocoles de communications liées à ces objets. En effet, l’échange de données dans ce contexte nécessite de tenir compte (au moins) des paramètres suivant :
    1. Autonomie énergétique souvent limitée
    2. Faible puissance des processeurs et taille réduite de la mémoire
    3. Disponibilité « aléatoire » de l’accès aux réseaux de communication

De nombreux protocoles cohabitent et la littérature du domaine foisonne d’exemples autour des réseaux dédiées (LORA, Sigfox, etc.) et des protocoles applicatifs (OPC-UA, MQTT, CoaP, XMPP) mais force est de constater que dans la réalité, ces solutions ne répondent pas toujours aux besoins des concepteurs qui leurs préfèrent encore le protocole HTTP. Celui-ci offre l’avantage d’implémenter un protocole applicatif (REST) en même temps qu’un protocole de transport de haut niveau (TCP/IP) permettant de passer les pare-feu. Cependant, la version actuel d’HTTP ne répond pas vraiment aux critères énoncés précédemment. Depuis quelques années émerge donc l’idée d’enrichir HTTP pour créer un protocole hybride qui mêlerait les avantages de REST avec ceux proposés par les mécanismes de type Publish/Subscribe (MQTT, AMQP, JMS, etc.). En attendant cette éventuelle évolution, peut-on envisager de mettre en place un mécanisme de type Pub/Sub avec le protocole Websocket au-dessus d’HTTP ?

  • Objectifs:
    1. Etudier et faire une synthèse des deux approches : REST et Pub/Sub
    2. Implémentez un PoC (proof of concept) d’une solution hybride qui met en œuvre un mécanisme de Pub/Sub sur Websocket. .
    3. Présenter un protocole de test pour valider ou invalider cette solution


La suite de Conway et la classification périodique des "éléments"

  • Tuteur : Pierre Hyvernat
  • La suite de Conway est la suite suivante : 1 ; 11 ; 21 ; 1211 ; 111221 ; ... Chaque terme est obtenu en "lisant" le terme précédent.
    • "1" : un "1" -> 11
    • "11" : deux "1" -> 21
    • "21" : un "2", un "1" -> 1211
    • "1211" : un "1", un "2", deux "1" -> 111221
    • etc.

Cette suite possède des propriétés étonantes données par le théorème "chimique", le théorème "arithmétique" et le théorème "cosmologique".

  • Objectifs :
    1. comprendre les énoncés de ces théorèmes, et l'idée de la preuve du premier.
    2. programmer la suite de Conway pour retrouver la classification des "atomes"
    3. écrire un programme pour calculer expérimentalement une approximation de la constante "lambda" ainsi que des fréquences respectives des différents atomes.
    4. écrire un programme pour calculer la suite de Robinson, une variante plus simple de la suite de Conway

Initiation à la démonstration sur ordinateur et certification de logiciel

  • Tuteur: Tom Hirschowitz
  • Résumé: [Coq] est un logiciel de mathématiques sur ordinateur, grâce auquel des programmes élaborés ont pu être certifiés ces dernières années.
  • Objectifs:
    1. prendre en main le logiciel [Coq] de démonstration sur ordinateur,
    2. programmer certaines démonstrations basiques en Coq,
    3. suivre le début du cours [Software Foundations],
  • Pour aller plus loin : Software Foundations est un cours assez long et très bien fait, il y aura suffisamment à faire. Eventuellement, selon l'intérêt de l'étudiant, étude des fondements mathématiques de Coq.
  • Liens pour démarrer

Algorithmes probabilistes/déterministes pour tester la primalité d'un entier

  • Tuteur : Sébastien Tavenas
  • Pouvoir tester si un entier est un nombre premier semble être une brique de base si l'on souhaite faire de l'arithmétique sur un ordinateur. Le crible d'Érathostène enseigné dans les petites classes se montre beaucoup trop lent en pratique. L'algorithme probabiliste utilisé le plus rapide est le test de Fermat. Or, si on regarde les algorithmes des librairies "génériques", on peut s'apercevoir que la fonction 'mpz_probab_prime_p' de la librairie 'gmp' sur c++ utilise un test probabiliste de Miller-Rabin, la fonction 'isPrime' de la classe 'Prime' dans java utilise aussi un test de Miller-Rabin mais qui est déterminisé, alors que la fonction 'isprime' de la librairie 'sympy' dans python effectue un test de Miller-Rabin si l'entier est plus petit que 2^64 et un test BPSW fort si l'entier est plus grand. Ainsi, une fonction déjà implémentée de test de primalité peut se tromper ou non, être instantanée ou moins. Que dire alors de l'algorithme polynomial déterministe et toujours correct proposé par AKS?
  • Objectifs :
    1. Comprendre quelques tests de primalité et comment l'aléatoire est utilisé dans ces algorithmes
    2. Comprendre la notion de nombre pseudopremier qui explique, entre autre, quand il vaut mieux utiliser le test de Fermat ou celui de Miller-Rabin
    3. Programmer quelques uns des ces tests et les comparer
    4. Essayer de dérandomiser ces tests à l'aide de hitting-sets précalculés

Dilemme du prisonnier

  • Tuteur: Gerald Cavallini
  • Résumé: Le dilemme du prisonnier caractérise en théorie des jeux une situation où deux joueurs auraient

intérêt à coopérer, mais où, en l’absence de communication entre les deux joueurs, chacun choisira de trahir l'autre si le jeu n'est joué qu'une fois.

On peut informatiquement modéliser ce dilemme à l’aide de matrices de gains et conserver la mémoire des choix de l’adversaire. Ce modèle appliqué à un grand nombre d’individus peut être utilisé pour comprendre l’émergence de stratégies stables dans l’économie, l’écologie, l’évolution des espèces ...

On peut visualiser spatialement les interactions entre individus en les représentants par des pixels et en leurs associant une couleur en fonction de leurs stratégies.

Dilemme.png


  • Objectifs
    1. Comprendre le dilemme du prisonnier
    2. Comprendre la notion de stratégie
    3. Penser un modèle spatiale pour « opposer » des individus qui appliquent des stratégies différentes
    4. Développer une interface pour visualiser dans le temps l’évolution d’une population d’individus adoptants des stratégies différentes.

Sujets réalisés (2017-2018)


Sujets proposés (2017-2018)

  • Segmentation d'image par détection de contours et algorithme "ligne de partage des eaux"
  • Initiation à la démonstration sur ordinateur et certification de logiciel
  • Fouille de données textuelles à partir des "Exercices de style" de R. Queneau
  • Transformées en distance, diagramme de Voronoi et applications en geometry processing
  • Pavages de Penrose


Segmentation d'image par détection de contours et algorithme "ligne de partage des eaux"

  • Tuteur: Jacques-Olivier Lachaud
  • Résumé: La segmentation d'image vise à identifier les régions d'intérêt dans une image. Typiquement, une région d'intérêt est une zone de l'image plutôt homogène (les pixels ont des valeurs proches) et le contour entre deux régions d'intérêt est tracé là où les valeurs subissent de fortes variations. La méthode de segmentation proposée ici suit ce principe en enchaînant deux calculs: (1) un premier traitement calcule une image "gradient" et fabrique une image dont les valeurs élevées correspondent à des zones de fortes variations, (2) le deuxième algorithme voit cette image comme un relief 3D et identifie ses bassins hydrographiques. Cette identification des lignes de partage des eaux permet de découper l'image en ses zones d'intérêt.
  • Objectifs:
    1. comprendre ce qu'est une image niveaux de gris ou couleur, ce qu'est le gradient d'une image et ce qu'on appelle segmentation d'image.
    2. décrire un algorithme de calcul du gradient d'une image, e.g. le filtre de Sobel, voire les convolutions par dérivées de Gaussienne.
    3. décrire le principe de ligne de partage des eaux ("watershed" en anglais), ses différentes définitions équivalentes, et les différents types d'algorithmes pour la calculer.
    4. Coder un programme de segmentation d'image, qui prend une image (niveaux de gris) en entrée, calcule son gradient, et extrait les bassins de sa ligne de partage des eaux.
  • Liens pour démarrer
    • [Watershed Wikipedia]
    • Luc Vincent and Pierre Soille. Watersheds in digital spaces: an efficient algorithm based on immersion simulations. In IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 13, Num. 6 (1991), pages 583–598 [PDF]

Initiation à la démonstration sur ordinateur et certification de logiciel

  • Tuteur: Tom Hirschowitz
  • Résumé: [Coq] est un logiciel de mathématiques sur ordinateur, grâce auquel des programmes élaborés ont pu être certifiés ces dernières années.
  • Objectifs:
    1. prendre en main le logiciel [Coq] de démonstration sur ordinateur,
    2. programmer certaines démonstrations basiques en Coq,
    3. suivre le début du cours [Software Foundations],
  • Pour aller plus loin : Software Foundations est un cours assez long et très bien fait, il y aura suffisamment à faire. Eventuellement, selon l'intérêt de l'étudiant, étude des fondements mathématiques de Coq.
  • Liens pour démarrer

Fouille de données textuelles à partir des "Exercices de style" de R. Queneau


Transformées en distance, diagramme de Voronoi et applications en geometry processing

  • Tuteur: Jacques-Olivier Lachaud
  • Résumé: Les nuages de points constituent une source de données géométriques importantes (cf LIDAR scanner, 3D scanner) et qui permet de construire des modèles géométriques 3D d'objets réels. La difficulté est de transformer ces nuages de points en des surfaces (souvent des surfaces triangulées, c'est-à-dire des triangles collés entre eux). Un outil essentiel dans ce processus est la transformée en distance, le diagramme de Voronoi (et son dual la triangulation de Delaunay). A partir de ces outils, des algorithmes existent pour reconstruire les surfaces, estimer la géométrie du nuage de point (sa normale par exemple), etc.
  • Objectifs:
    1. Comprendre ce qu'est une distance, une transformée en distance, et un diagramme de Voronoi. Comprendre ce qu'est la stabilité d'une fonction.
    2. Identifier les propriétés des diagrammes de Voronoi, de leur dual la triangulation de Delaunay, et comprendre leurs variantes comme les diagrammes de puissance
    3. Identifier le lien avec l'axe médian et les squelettes
    4. Décrire les principaux algorithmes de calcul des transformées en distance et du diagramme de Voronoi, pour des nuages de point quelconques ou pour des nuages de points à coordonnées entières.
    5. Présenter un algorithme de reconstruction de surface utilisant le diagramme de Voronoi
    6. Coder un algorithme de calcul du diagramme de Voronoi et, si le temps le permet, un algorithme de reconstruction de surface.

Pavages de Penrose

  • Tuteur : Pierre Hyvernat
  • Résumé : le "cerf-volant" et la "fléchette" de Penrose sont deux tuiles qui permettent de recouvrir le plan, mais uniquement de manière non-périodique. Autrement dit, les pavages correspondants ne sont pas obtenus en répétant un même motif de manière régulière. A cause de ceci, il n'est pas évident de générer un tel pavage.

P2.png

  • Objectifs
    1. comprendre les notion de pavage périodique, non périodique et apériodique,
    2. comprendre la méthode "inflation / déflation" pour générer des pavages de Penrose des différents types,
    3. comprendre le lien entre les 2 (ou 3) types de pavage de Penrose
    4. écrire un programme permettant de générer de tels pavages : avec la méthode "inflation / déflation" et avec la méthode "grille de de Bruijn"
    5. utiliser ces méthodes pour générer d'autres types de pavages apériodique.


Algorithmes d'analyse syntaxique

  • Tuteur : Pierre Hyvernat
  • Résumé : le code source d'un programme, d'un fichier de configuration d'un serveur de base de données ou le code d'une page web sont des données textuelles et structurées. Il est possible de définir exactement quelles données sont correctes, et quelle est leur signification. (Cela est beaucoup plus difficile pour des textes en langue naturelle par exemple.) En ce sens, il est possible de lire, d'interpréter ces données à l'aide d'un programme. On parle d'analyseur syntaxique ou de parseur. Il existe de nombreux outils pour faire ça automatiquement, mais il est parfois important (et toujours intéressant) de comprendre les mécanismes correspondant. C'est ce que ce stage propose de faire.
  • Objectifs :
    1. étudier la formalisation du problème à travers la notion de langage et les premiers étages de la hiérachie de Chomsky (langages réguliers et grammaires hors contexte).
    2. comprendre le lien entre les langages et les automates (automates finis / automates à pile)
    3. implémenter un parseur "from scratch" et le tester sur des petits exemples simples, "à la main", soit en calculant "à la volée" la sémantique d'un langage, soit en produisant des "arbres de syntaxe abstraits", qui pourront être analysés par la suite,
    4. comprendre les restrictions souvent imposées sur les grammaires afin d'améliorer l'efficacité du parseur (LL*(k), LR, etc.)
    5. à partir de là, de nombreuses pistes sont ouvertes :
      • essayer d'écrire un petit outils qui puisse lire une grammaire, et générer un parseur pour cette grammaire,
      • comparer l'approche "automate" avec l'approche "combinateurs" et "parseur récursifs"
      • améliorer l'efficacité des parseurs produits
      • ajouter des fonctionnalités,
      • ...

Sujets réalisés (2016-2017)


Sujets proposés (2016-2017)

Algorithme de rendu de scène 3D par Z-buffer

  • Tuteur: Jacques-Olivier Lachaud
  • Résumé: Le Z-buffer est un algorithme classique de rendu de scène 3D. C'est celui (avec quelques variantes) qui est implémenté dans nos cartes graphiques 3D et qui permet de visualiser des scènes extrêmement complexes en temps réel (typiquement 24 image/s).
  • Objectifs:
    1. décrire le principe de la projection 3D vers 2D
    2. décrire la rastérisation des triangles sur une image en pixel
    3. expliquer le principe du Z-buffer qui permet de gérer le fait que certains objets sont cachés par d'autres
    4. expliquer comment les couleurs sont calculées par pixel
    5. indiquer les qualités et limitations de l'algorithme
  • Pour aller plus loin
    1. mettre du code démo (WebGL) avec quelques explications sur le pipeline graphique OpenGL
    2. expliquer comment on peut utiliser cet algorithme pour calculer des ombres (shadow map)
  • Liens pour démarrer

Traitement d'image

  • Tuteur: Jacques-Olivier Lachaud
  • Résumé: Le traitement d'image rassemble tous les algorithmes utilisés pour transformer les images, les améliorer, éliminer certaines perturbations, augmenter ou diminuer le contraste, changer les couleurs vers d'autres couleurs, éliminer le flou ou les yeux rouges, faire du cartooning pour un rendu moins photo-réaliste, etc.
  • Objectifs:
    1. identifier les grandes familles de traitement: restauration, égalisation, élimination du flou de déplacement, segmentation, etc
    2. identifier les grandes familles de techniques: filtrage spatial, filtrage fréquentiel, optimisation, etc
    3. comprendre les points communs et différences entre le traitement des images noir et blanc et le traitement des images couleurs.
    4. choisir un ou deux algorithmes de traitement et les expliquer en détails
  • Pour aller plus loin
    1. Coder un algorithme de traitement d'image simple (e.g, un filtrage médian, ou un algo qui transporte les couleurs d'une photo vers une autre photo)


Nim et la théorie des jeux impartiaux

  • Tuteur: Pierre Hyvernat
  • Étudiant : Luca Chapelle
  • Le jeu de Nim (aussi appelé jeu des allumettes) est l'un des premiers jeux ayant été analysé mathématiquement (par Charles Bouton en 1901). Les stratégies gagnantes peuvent être calculées en utilisant le développement en base 2 des nombres, et l'opération d'"addition de Nim" (XOR). La théorie de ce type de jeux (jeux "impartiaux") est assez simple, mais de nombreuses instances de jeux sont encore non résolues.
  • Objectifs:
    1. comprendre la théorie du jeu de Nim (et la programmer)
    2. comprendre le théorème de Sprague Grundy qui montre que tout jeu impartial est équivalent à un jeu de nim
    3. regarder quelques autres exemples de tels jeux : jeu de Nim déguisés, ou jeux véritablement différents
    4. programmer une version naịve de recherche de stratégie basée sur le théorème de Sprague-Grundy pour quelques jeux

La suite de Conway et la classification périodique des "éléments"

  • Tuteur : Pierre Hyvernat
  • La suite de Conway est la suite suivante : 1 ; 11 ; 21 ; 1211 ; 111221 ; ... Chaque terme est obtenu en "lisant" le terme précédent.
    • "1" : un "1" -> 11
    • "11" : deux "1" -> 21
    • "21" : un "2", un "1" -> 1211
    • "1211" : un "1", un "2", deux "1" -> 111221
    • etc.

Cette suite possède des propriétés étonantes données par le théorème "chimique", le théorème "arithmétique" et le théorème "cosmologique".

  • Objectifs :
    1. comprendre les énoncés de ces théorèmes, et l'idée de la preuve du premier.
    2. programmer la suite de Conway pour retrouver la classification des "atomes"
    3. écrire un programme pour calculer expérimentalement une approximation de la constante "lambda" ainsi que des fréquences respectives des différents atomes.
    4. écrire un programme pour calculer la suite de Robinson, une variante plus simple de la suite de Conway

Initiation à la démonstration sur ordinateur et certification de logiciel

  • Tuteur: Tom Hirschowitz
  • Résumé: [Coq] est un logiciel de mathématiques sur ordinateur, grâce auquel des programmes élaborés ont pu être certifiés ces dernières années.
  • Objectifs:
    1. prendre en main le logiciel [Coq] de démonstration sur ordinateur,
    2. programmer certaines démonstrations basiques en Coq,
    3. suivre le début du cours [Software Foundations],
  • Pour aller plus loin : Software Foundations est un cours assez long et très bien fait, il y aura suffisamment à faire. Eventuellement, selon l'intérêt de l'étudiant, étude des fondements mathématiques de Coq.
  • Liens pour démarrer

Calculabilité et modèles de calcul

  • Tuteur: Rodolphe Lepigre
  • Résumé: Une fonction f sur l'ensemble des entiers naturels est dite calculable s'il existe une procedure effective (ou un algorithme) qui permet, étant donné un entier n, de calculer f(n) en temps fini. Il existe divers modèles de calcul qui permettent de représenter toutes les fonctions calculables : machines de Turing, λ-calcul, automates cellulaires, ...
  • Objectifs:
    1. comprendre la notion de fonction calculable,
    2. comparer l'ensemble des fonctions à l'ensemble des fonctions calculables,
    3. regarder et comparer quelque modèles de calcul,
    4. programmer un modèle de calcul et comprendre les limitations pratiques.

Génération et résolution de labyrinthes

  • Tuteur: Jacques-Olivier Lachaud Xavier Provençal
  • Résumé: On veut générer des labyrinthes aussi grands et complexes que possible, avec des murs dans une grille carré voire d'autres domaines. Comment faire pour qu'il y ait toujours un chemin de l'entrée à la sortie ? Comment faire pour qu'il n'y ait qu'un chemin ? Ensuite, comment trouver la sortie quand on est perdu dans le labyrinthe.
  • Objectifs:
    1. Comprendre comment représenter avec une structure de données un labyrinthe
    2. Voir le lien avec la théorie des graphes et voir que le problème se résout de la même façon pour des grilles carrées, hexagonales ou autres.
    3. Comprendre l'algorithme d'arbre couvrant minimum
    4. Comprendre le principe du parcours en profondeur et de la récursivité
  • Pour aller plus loin
    1. coder la génération d'un labyrinthe et sa visualisation
  • Liens pour démarrer

Pavages par polyomino

  • Tuteur: Xavier Provençal
  • Résumé : On s'intéresse aux pavages du plan par des tuiles formées de petits carrés collés les uns aux autres, appelé "polyominos". Étant donné une tuile, peut-on paver le plan ? Si oui, avec quelles opérations (translation et/ou rotations et/ou réflexions) Une fois un pavage réalisé, on observe ses propriétés. Quelles symétries ? Le pavage est-il identique du point de vue de chacune des tuiles ? Si ce n'est pas le cas, en combien de classes peut-on diviser ces tuiles ?

On s'intéressera aussi à des propriétés connexes. Au lieu de paver tout le plan, on peut essayer de paver une région finie donnée. Plus localement, peut-on encercler complètement une tuile avec des copies d'elle-même, sans former de trous ? Si oui, peut-on faire de même avec la proto-tuile formée par la tuile de départ et toutes ses copies ? Si oui, combien de fois peut-on répéter l'opération ?

  • Objectifs :
    1. Comprendre les différentes classes de pavages (isohédral, k-isohédral, anisohédral).
    2. Pour chacun des sept types de pavages "isohédraux", comprendre le lien entre les symétries du pavages et la caractérisation des tuiles qui le réalisent.
    3. Pour un pavage k-isohédral, identifier les "classes d'équivalences" et le "domaine fondamental".
  • Pour aller plus loin :
    1. Coder la génération de tuiles capables de paver le plan en fonction pour une classe de pavages donnée.
    2. Étudier et implémenter certains algorithmes pour le pavages d'un domaine fini.
  • Liens pour démarrer
Récupérée de « http://os-vps418.infomaniak.ch:1250/mediawiki/index.php?title=VISI201_CMI_:_visite_de_laboratoire&oldid=12643 »