Approximation numérique de calculs intégraux

Les calculs intégraux sont de nos jours beaucoup utilisés pour la création et la modification de modélisation d'éléments, ou permettre l'analyse de fonctions. Ces calculs sont parfois compliqués et nécessitent parfois beaucoup de travail. Pour nous aider, il nous est possible d'utiliser des machines qui peuvent réaliser ces calculs à notre place.

Pour cela, il nous faut construire des méthodes de calculs qui nous permettrons de réaliser ces calculs. Nous traiterons ici de 2 types de méthodes: les méthodes de quadratures de Gauss et les méthodes probabilistes.

Les méthodes de quadratures

Explication

Les méthodes de Quadrature de Gauss permet de remplacer le calcul d'une intégrale par la somme pondérée prise en certains points du domaine d'intégration.

Selon les fonctions qui sont entrées en paramètre, ainsi que le degré de précision que nous souhaitons obtenir, il existe différentes méthodes pour permettre les calculs d'intégrations.

Liste de différentes méthodes étudiée

Nous étudierons ici plusieurs méthodes:

- la méthode des rectangles
- la méthode du point du milieu
- la méthode des trapèzes
- la méthode de Simpson

Méthode des rectangles

La méthode des rectangle consiste à créer une suite d'intervalles régulier. Nous utiliserons le point le plus petit de chaque intervalle pour créer un rectangle de longueur f(minimum Intervalle) et de largeur la taille de l'intervalle. Selon les méthodes de quadratures, la somme de l'aire de tous ces carrés permet d'approximer la valeur de l'intégrale de la fonction f.

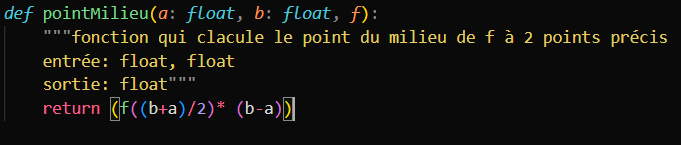
Méthode du point du milieu

La méthode du point du milieu consiste à créer une suite d'intervalles régulier. Nous utiliserons le point le plus petit de chaque intervalle pour créer un rectangle de longueur f((maximum Intervalle + minimum Intervalle)/2) et de largeur la taille de l'intervalle. Selon les méthodes de quadratures, la somme de l'aire de tous ces carrés permet d'approximer la valeur de l'intégrale de la fonction f.

Méthode des trapèzes

La méthode du point du milieu consiste à créer une suite d'intervalles régulier. Nous utiliserons le point le plus petit de chaque intervalle pour créer un trapèze dont l'une des longueur est égale à f((maximum Intervalle), l'autre côté égal à f(minimum Intervalle) et de hauteur la taille de l'intervalle. Selon les méthodes de quadratures, la somme de l'aire de tous ces trapèzes permet d'approximer la valeur de l'intégrale de la fonction f.

Méthode de Simpson

test 252

Différence entre les méthodes

La plus grande différence entre toutes les méthodes est la précision des différentes méthodes atteintes avec un nombre d'intervalles donné.

Chacune de ces méthodes permet une précision différentes pour le calcul des intégrales: le nombre d'intervalle nécessaire pour obtenir un résultat de même précision est donc différent selon les méthodes.

Par exemple, la méthode de Simpson nécessitera un nombre d'intervalle plus petit que la méthode des rectangles pour que le résultat soit suffisamment précis.

Les programmes de calculs

Le programme général

Avant le calcul de notre intégrale, nous devons indiquer à notre fonction la taille des intervalles que nous allons calculer.

Pour cela, nous utilisons la bibliothèque numpy de Python, qui nous permet de créer des liste de nombres espacé d'une certaine valeur, toujours identique, et dépendant du nombre d'éléments dans la liste.

voici les lignes de codes qui permettent cela:

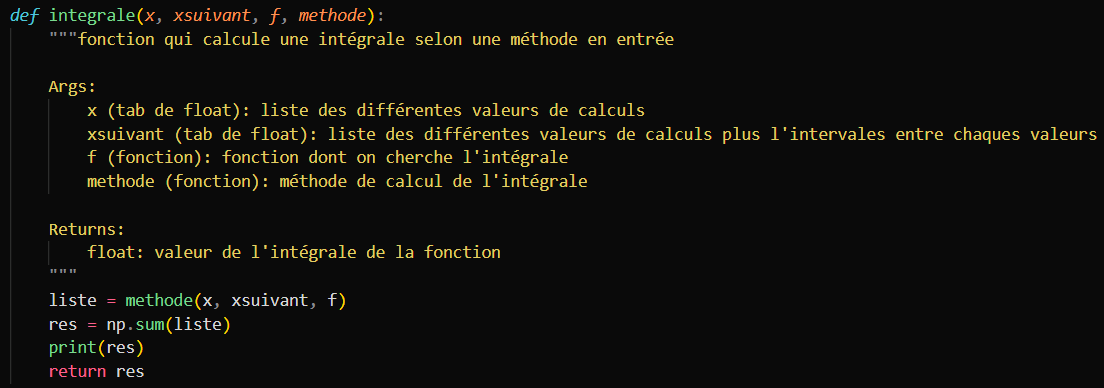
Le programme de calcul des différentes intégrales selon un nombre d'intervalle donné suit une procédure qui est toujours la même, malgré la méthode utilisée qui est différente.

Voici le programme de calcul après optimisation:

Cette procédure fonctionne ainsi:

- on calcule une liste contenant l'aire de tous les intervalles créé par une méthode donnée pour une fonction donnée
- on additionne tous les éléments de cette liste
- on renvoie le résultat de cette fonction

L'écriture des méthodes

Chacune des méthodes que nous souhaitons utiliser sont ensuite implémenté dans le code.

Voici une liste des différentes méthodes que nous avons pu réaliser:

Méthode des rectangles

Méthode du point du milieu

Méthode des trapèzes

Méthode de Simpson

L'écriture des fonctions utilisables

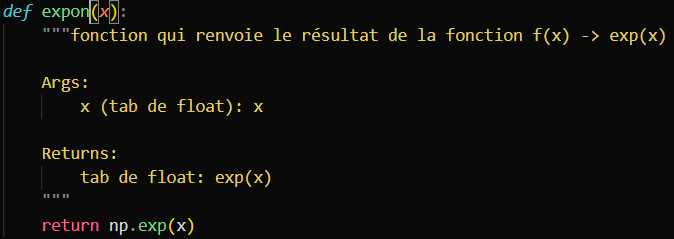
Pour terminer, nous pouvons recréer les différentes fonctions utilisable telles que sinus, cosinus ou exponentielle.

Voici 2 exemples de telles fonction:

Le calcul de l'erreur

Toutes ces méthodes possèdent un taux d'erreur qui varie selon le nombre et la taille des intervalles utilisées ainsi que l'erreur intrinsèque de la méthode. L'erreur d'une fonction se calcule en partie sur la dérivé n ème de la fonction de travail, qui peut, selon certaines, être égal à 0 si on les associes à une certaine méthode.

Le calcul de l'erreur d'une fonction se définie ainsi:

Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle f(xi) + (x - xi)f^(n)(ui) , ui ∈[xi, xi + h]}

Ou n représente le n de la dérivé n ème de la fonction.

Pour la méthode des rectangles, le calcul de l'erreur s'écrit de cette manière:

Échec de l’analyse (erreur de syntaxe): {\displaystyle f(xi) + (x - xi)f^(0)(ui) , ui ∈[xi, xi + h]}

Après analyse du calcul, on peut remarquer qu'il est exact pour toute fonctions dont la formule de base est une constante.

En comparaison, pour la méthode des trapèzes, le calcul de l'erreur s'écrit de cette manière:

Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle f(xi) + (x - xi)f^(2)(ui) , ui ∈[xi, xi + h]}

Après analyse du calcul, on peut remarquer qu'il est exact pour toute fonctions dont la formule de sa dérivée seconde est une constante.

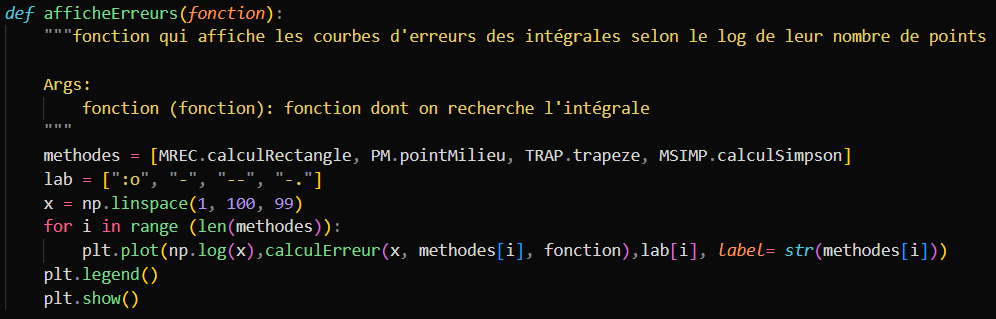
La fonction d'affichage de l'erreur

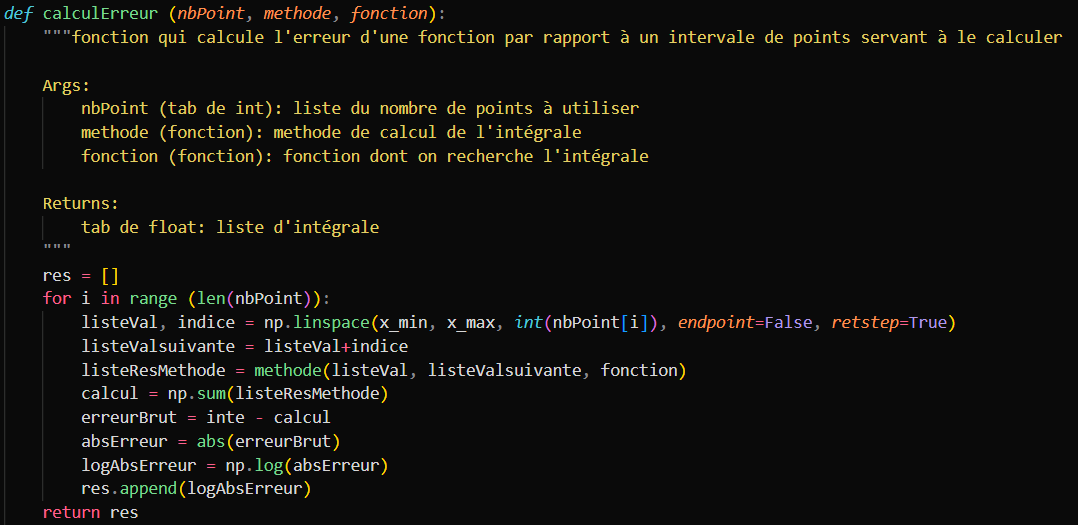
Pour pouvoir réaliser une véritable comparaison entre ces erreurs, nous avons réalisé un programme qui calcul et trace sur un graphique l'évolution des erreurs de chaque fonctions en fonction du nombre de points utilisés pour faire les intervalles.

La fonction de calcul

Nous avons donc commencer par créer une fonction qui calcule le taux d'erreur d'une fonction selon le nombre de point qui à servit à faire le calcul.

voici à quoi ressemble la fonction:

test 252

La fonction d'affichage

Telle quelle, ces listes ne nous donnent pas beaucoup d'informations.

Nous avons donc réaliser une fonction supplémentaire qui nous permet d'afficher un graphe qui compare les différentes fonctions entre elles.

Voici la fonction ainsi créé.

test 252

Les méthodes probabilistes

Explication:

Il existe une autre manière de réaliser le calcul d'une intégrale qui utilise la probabilitée.

Nous étudierons ici la méthode de Monte-Carlo. Elle consiste, en quelques mots, à "jeter" des points sur un espace de définition donné, puis de vérifier, pour chaque point, si il appartient ou pas à l'aire sous la fonction. Nous réalisons ensuite une division du nombre de points qui appartiennent à cette aire par le nombre de point total que nous avons placé dans l'espace de travail.

Cela nous donnera la part de notre espace de travail qui est occupé par l'aire de la courbe de la fonction.

Il suffit ensuite de multiplier se résultat par l'aire de notre espace de travail pour obtenir une approximation de la valeur de l'intégrale d'une fonction pour un intervalle donnée.

Points faibles de la méthode

Cette méthode parait simple et facile d'utilisation en apparence, mais possède plusieurs problèmes:

- l'espace de travail doit être recalculer lors de chaque nouveau calcul pour bien correspondre à l'espace de définition de la fonction utilisée. En effet, si l'espace de calcul est trop petit ou trop grand, il sera impossible de calculer correctement, voir parfois d'espérer obtenir un résultat qui peut fonctionner correctement.
- Cette méthode peut réaliser en théorie n'importe quel calcul d'intégrale, mais nécessite toujours un nombre importants de point pour être vraiment efficace, et ce nombre augmente très vite par rapport à la taille de l'intervalle de travail.

Points forts de la méthode

Mais, malgré ces quelques problèmes, cette fonction possède plusieurs gros avantages:

- Il est très facile de la modifier pour, par exemple, passé  d'une fonction définie de R à R à une fonction définie de R² à R.
- Si l'espace de travail est bien définie, et que le nombre de points que nous utilisons pour réaliser les calculs est assez grand, il est possible de réaliser n'importe quel calcul d'intégrale sur n'importe quelle fonction en entrée.

Les programmes de calculs

Nous avons donc réalisé un programme qui réalise cette méthodes de calcul.

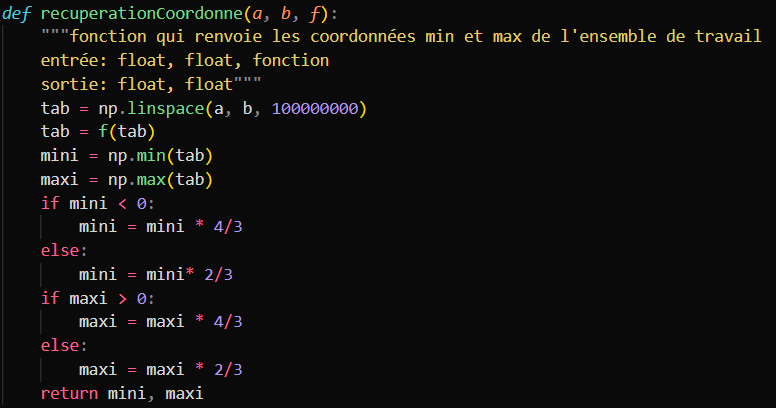
Définition de l'espace de travail

Nous commençons tous d'abord par créer notre espace de travail selon l'intervalle ou nous souhaitons calculer notre intégrale ainsi que la fonction que nous allons utiliser.

Voici le code de cette fonction:

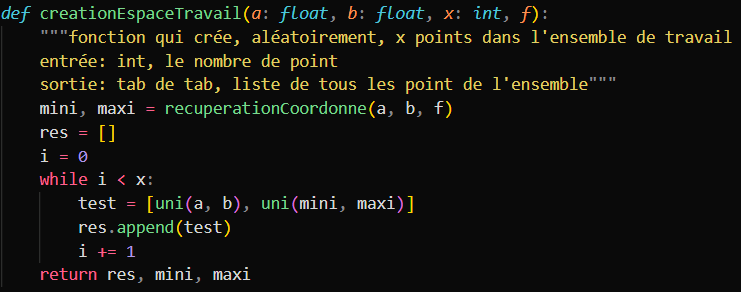
Création des points dans notre espace de travail

Nous avons ensuite créé une fonction qui permet de terminer la création de notre espace de travail, en créant une liste de différend points placer aléatoirement appartenant à notre espace de travail.

Voici le code de cette fonction:

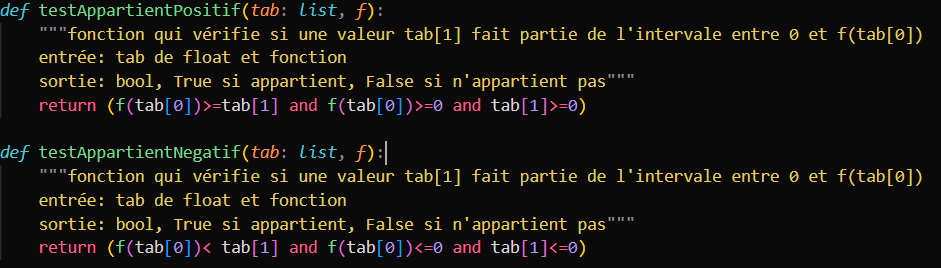
Vérification à l'appartenance du point à l'aire de la courbe

Après cela, nous avons réaliser 2 fonctions de vérification pour connaitre l'emplacement d'un point par rapport à la courbe de notre fonction et à l'abscisse du graphique.

Nous avons donc, grâce à ces vérification, obtenir le nombre de points qui appartiennent à l'aire de la courbe.

Voici le code de ces fonctions:

Division

Nous avons aussi réaliser une dernière fonction, qui permet de réaliser la division du nombre de point dans l'aire de la fonction par le nombre de points qui ont été mis sur l'espace de travail total.

Voici le code de cette fonction:

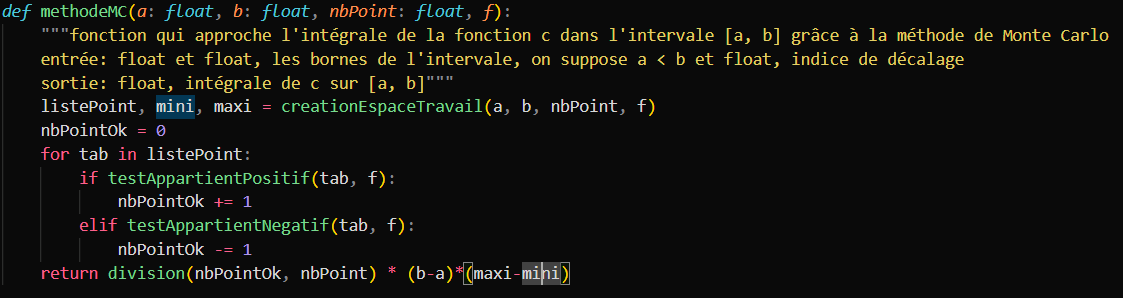
Tronc principale de la fonction

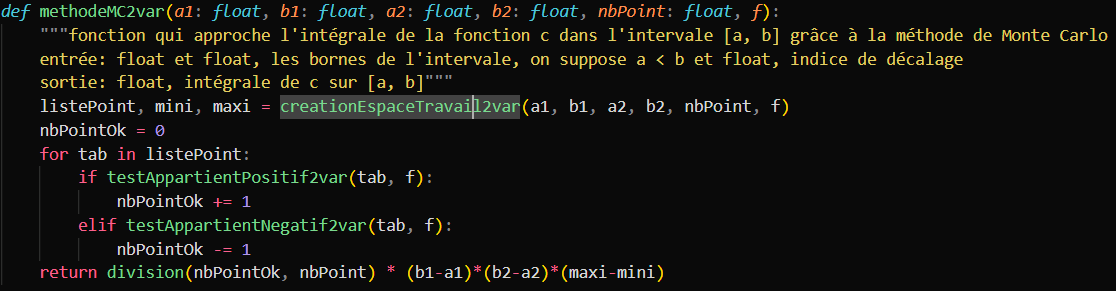
Une fois toutes ces fonctions créé, nous les avons associées toutes ensemble pour créer la fonction finale, qui permet de calculer l'intégrale d'une fonction selon un nombre de points à placer à l'intérieur ainsi que d'une fonction d'étude.

Voici le code de cette fonction.

Annexe: Méthode de Monte-Carlo pour une fonction définie de R² à R

Dans le cadre de notre recherche sur la méthode de Monte-Carlo, nous avons pu réaliser une fonction qui, en exploitant le même fonctionnement que la fonction de Monte-Carlo, mais qui prend cette fois-ci une fonction définie de R² vers R.

Plusieurs fonctions on donc du être modifiées:

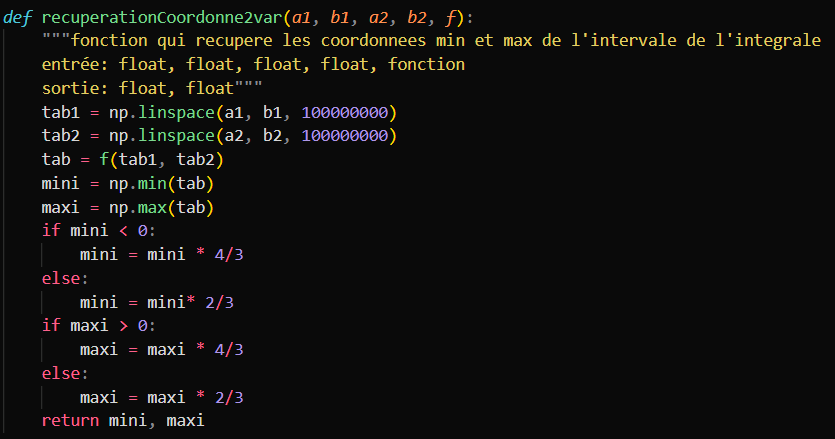
Définition de l'espace de travail

Nous avons du revoir la définition de notre espace de travail pour qu'il puisse créer un espace utilisable pour une fonction à 2 variables.

Voici le code de ce programme:

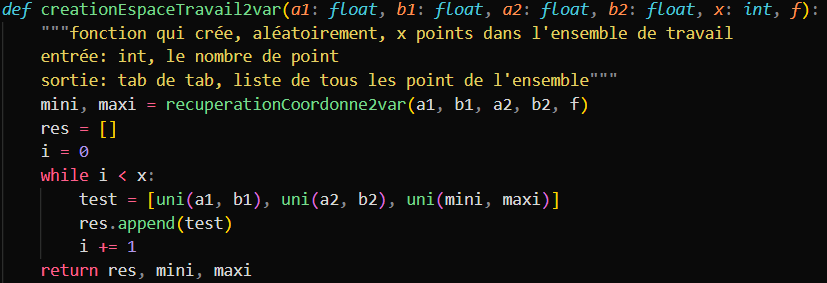
Création des points dans notre espace de travail

Les points possédants désormais 3 coordonnées au lieux de 2, nous avons du revoir leur créations ainsi que leur positionnement dans l'espace de travail.

Voici le code de ce programme:

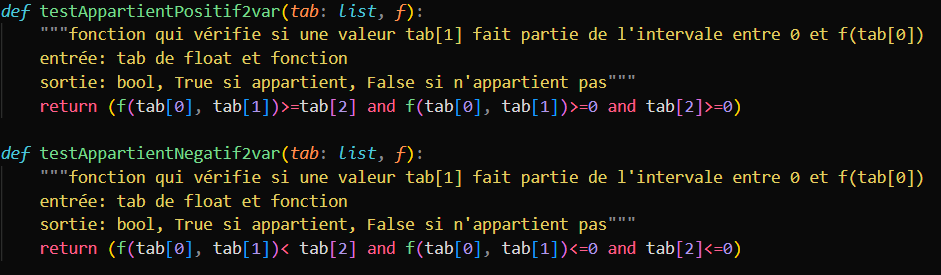
Vérification à l'appartenance du point à l'aire de la courbe

Les fonctions de vérification des points doivent aussi être modifier pour pouvoir obtenir correctement les valeurs rechercher.

Nous avons donc, grâce à ces vérification, obtenir le nombre de points qui appartiennent à l'aire de la courbe.

Voici le code de ces fonctions:

Tronc principale de la fonction

Le tronc principal, quand à lui, doit prendre en compte les nouvelles fonctions réalisées.

Voici le code de cette fonction.