« Transformée-de-Hough » : différence entre les versions
Aucun résumé des modifications |
|||
| (5 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
La transformée de |
La transformée de Hough est une technique utilisée pour détecter des formes géométriques dans une image. Ces formes peuvent aussi bien être des droites que des cercles ou autre. L'idée est de représenter les différents points d'une image dans "l'espace de Hough" dont les paramètre seront ceux de la forme que l'on cherche. Ce qui fait que nos points pourront être tracés dans l'espace de Hough sous la forme de courbes. Les endroits ou ces courbes se croiseront correspondront aux paramètre de la forme détectée dans l'image d'origine. |
||
[[Fichier:image_origine.png|thumb|200px|left|Image d'origine]] [[Fichier:detectee.png|thumb|200px|none|droite détectée (En rouge)]] |
|||
[[Fichier:hough1.png]] |
|||
== Algorithme naïf == |
|||
=== Principe === |
|||
Nous allons commencer par travailler avec des droites. Le principe de la transformée de Hough se base sur l'utilisation de l'équation de la forme recherchée et donc nous allons commencer en utilisant l'équation cartésienne d'une droite.<br><br> |
|||
<math>y = m*x + b</math><br><br>m : coefficient directeur<br>b : intersection entre la droite et l'axe des ordonnées |
|||
<br> |
|||
Nous allons ensuite créer un nouvel espace ou chaque point est en fonction de m et b et non pas de x et y on appellera cet espace l'espace de Hough |
|||
Une droite dans l'espace normal est donc un point dans cet espace car il a ses coordonnées m et b définie par conséquent un point dans l'espace normal sera donc une droite dans l'espace de Hough. |
|||
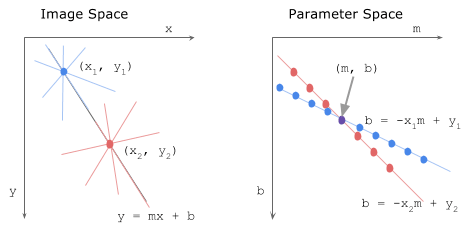
[[Fichier:hough_space.png|thumb|600px|left|Les points rouges et bleus à droite sont tracés dans l'espace de Hough à gauche]] |
|||
Dernière version du 20 mai 2023 à 16:28
La transformée de Hough est une technique utilisée pour détecter des formes géométriques dans une image. Ces formes peuvent aussi bien être des droites que des cercles ou autre. L'idée est de représenter les différents points d'une image dans "l'espace de Hough" dont les paramètre seront ceux de la forme que l'on cherche. Ce qui fait que nos points pourront être tracés dans l'espace de Hough sous la forme de courbes. Les endroits ou ces courbes se croiseront correspondront aux paramètre de la forme détectée dans l'image d'origine.
Algorithme naïf
Principe
Nous allons commencer par travailler avec des droites. Le principe de la transformée de Hough se base sur l'utilisation de l'équation de la forme recherchée et donc nous allons commencer en utilisant l'équation cartésienne d'une droite.
m : coefficient directeur
b : intersection entre la droite et l'axe des ordonnées
Nous allons ensuite créer un nouvel espace ou chaque point est en fonction de m et b et non pas de x et y on appellera cet espace l'espace de Hough
Une droite dans l'espace normal est donc un point dans cet espace car il a ses coordonnées m et b définie par conséquent un point dans l'espace normal sera donc une droite dans l'espace de Hough.