Recherche de chemin en temps réel par A*

Introduction

Le programme A* (A-star) est un algorithme de recherche de chemin utilisé dans les domaines de l'intelligence artificielle, de la robotique et des jeux vidéo. Il est principalement utilisé pour trouver le chemin le plus court entre un point de départ et un point d'arrivée dans un graphe pondéré.

Définition

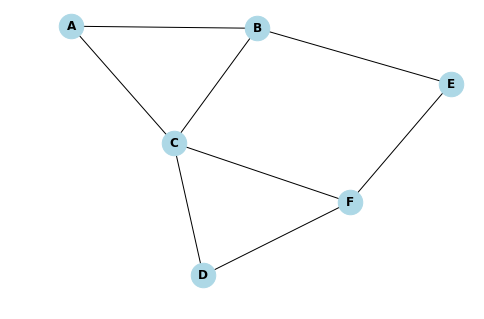Graphe comprenant 6 nœuds allant de A à F

Graphe : Comme vous l’avez vu ci-dessus un graphe contient des nœuds et des arrêtes. Il peut être orienté lorsque le sens est fixe (On pourrait passer du point A à B mais pas du point B à A) mais dans notre cas il sera non orienté.

Nœud : Ils sont en bleu sur l’exemple ci-dessus. Ils sont les intersections entre les différentes arrêtes.

Distance : La distance est celle qu’on a entre deux nœuds.

Cout : Il est composé des distances parcourus plus le nœud futur.

Heuristique : Il nous sert à orienter notre recherche, il est composé du cout et de la distance à vol d’oiseau entre le nœud et l’arrivé

Fonctionnement

Le fonctionnement de l'algorithme A* repose sur une exploration de différent paramètre tel que l'heuristique à venir, les coûts passés et les estimations heuristiques. L'algorithme maintient une liste de nœuds à explorer, en choisissant à chaque étape le nœud avec le coût total le plus faible. Il utilise une fonction d'évaluation qui combine le coût passé (g(n)), qui représente le coût cumulé pour atteindre un nœud donné depuis le point de départ, et une estimation heuristique du coût restant (h(n)), qui estime le coût pour atteindre la destination depuis le nœud donné. La fonction d'évaluation est définie comme f(n) = g(n) + h(n).

Ses avantages

1. Efficacité : L'un des principaux avantages d'A* est son efficacité par rapport à d'autres algorithmes de recherche de chemin. Grâce à l'utilisation d'une heuristique pour guider la recherche, A* est capable d'explorer sélectivement les zones du graphe qui sont plus susceptibles de conduire à la solution optimale. Cela permet d'éviter d'explorer inutilement des chemins plus longs, ce qui réduit le temps de calcul nécessaire pour trouver la solution.

2. Optimalité : A* garantit de trouver le chemin le plus court dans un graphe pondéré, à condition que l'heuristique utilisée soit admissible. Cela signifie que si une solution existe, A* la trouvera. L'utilisation d'une fonction d'évaluation qui combine le coût réel et l'estimation heuristique permet à A* de faire des choix informés tout en garantissant que la solution trouvée est bien la plus courte.

Ses limites

1.Complexité temporelle : La complexité de l'algorithme peut augmenter considérablement avec la taille du graphe et le nombre de nœuds à explorer.

2.Coût heuristique : L'efficacité de l'algorithme dépend de la qualité de l'estimation heuristique. Si l'estimation est trop pessimiste ou inexacte, l'algorithme peut être moins efficace ou ne pas trouver la solution optimale.

3.Problèmes de chemin à coûts variables : L'algorithme A* est mieux adapté aux graphes où les coûts des arêtes sont fixes. Dans les graphes avec des coûts variables, il peut ne pas être approprié ou nécessiter des adaptations supplémentaires.