« Surfaces polygonales et surfaces de subdivision » : différence entre les versions
| Ligne 34 : | Ligne 34 : | ||
w_face : <strong style="color:#ff0000">[ |
w_face : <strong style="color:#ff0000">[<strong style="color:#7ED957">0</strong>]</strong> |
||
w_vertex : <strong style="color:#38B6FF">[<strong style="color:#7ED957">1,3,5</strong>]</strong> |
w_vertex : <strong style="color:#38B6FF">[<strong style="color:#7ED957">1,3,5</strong>]</strong> |
||
Version du 8 mai 2024 à 15:39
Élève : Vetea STOLL
Tuteur : Jacques Olivier Lachaud
Définitions
Surface
Structure de données demie arêtes ailées
Description
Dans cette structure de données les arêtes (ex point A et B) sont décomposée en 2 demie arêtes (A vers B et B vers A) sont définies implicitement par un indice.
Chaque demie arête a une demie arête suivante (next) une demie arête opposée (opp) un point vers lequel la demie arête pointe (to_vertex) et l'indice de la face à laquelle la demie arête est associée (face), si il n'y a pas de face on mettra -1 par convention.
Pour accéder à ces paramètres on définie des listes de longueur n avec n nombre de demie arêtes pour chaque paramètre.
Les faces ont une demie arête associée de façon arbitraire (w_face) également pour les points (w_vertex).
On fera également des listes pour ces paramètres de longueur n avec n nombre de face et nombre de points.
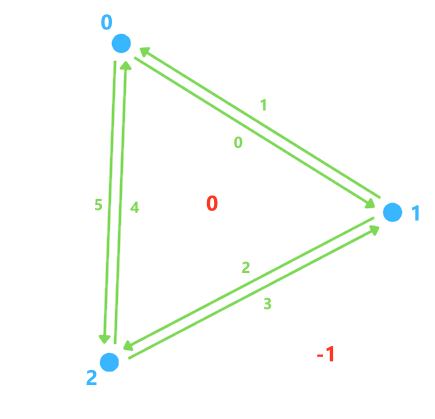
La structure de donnée d'un triangle ressemblera à ça :
next : [2,5,4,1,6,3]
opp : [1,0,3,2,5,4]
to_vertex : [1,0,2,1,0,2]
face : [0,-1,0,-1,0,-1]
w_face : [0]
w_vertex : [1,3,5]