« VISI401 CMI : bibliographie scientifique » : différence entre les versions
| (9 versions intermédiaires par un autre utilisateur non affichées) | |||
| Ligne 20 : | Ligne 20 : | ||
== sujets 2024-2025 == |
== sujets 2024-2025 == |
||
=== [[Algorithmes de colorations de graphes]] === |
|||
''' Tuteur :''' Valentin Gledel |
|||
''' Résumé :''' Un [https://fr.wikipedia.org/wiki/Th%C3%A9orie_des_graphes graphe] est un ensemble de sommets et un ensemble d’arêtes sur ces sommets. Une [https://fr.wikipedia.org/wiki/Coloration_de_graphe coloration propre] d'un graphe est une assignation de couleurs à chaque sommet du graphe telle que chaque paire de sommets reliée par une arête a des couleurs différentes. |
|||
<table> |
|||
<tr> |
|||
<td>[[File:Graph.jpg|400px]]</td> |
|||
<td>[[File:Coloration.jpg|400px]]</td> |
|||
<td>[[File:Impropre.jpg|400px]]</td> |
|||
</tr> |
|||
<tr> |
|||
<td>Un graphe</td> |
|||
<td>Une coloration propre de ce graphe</td> |
|||
<td>Une coloration impropre du graphe</td> |
|||
</tr> |
|||
</table> |
|||
Connaître le nombre minimum de couleurs permettant de colorer proprement un graphe est un problème NP-difficile. Cependant, il existe des algorithmes de coloration de graphe permettant de trouver une coloration propre en fonction du nombre de voisins maximums d'un sommet. L'objectif de ce sujet est d'implémenter certains de ces algorithmes. |
|||
'''Objectifs :''' |
|||
# implémenter l'algorithme de coloration glouton d'un graphe |
|||
# implémenter l'amélioration de cet algorithme en utilisant la dégénérescence du graphe |
|||
# implémenter l'algorithme issus du théorème de Brooks |
|||
# éventuellement, implémenter un algorithme de coloration d'arêtes |
|||
# éventuellement, implémenter un algorithme de transformation du problème SAT en problème de coloration |
|||
=== [[Algorithme de Ukkonen / algorithme SA-IS]] === |
|||
'''Tuteur :''' Pierre Hyvernat |
|||
'''Résumé :''' L'arbre des suffixes est une structure de données qui permet de répondre très rapidement à de nombreuses requêtes du style "est-ce que la chaine ''p'' apparait dans la chaine ''S'' ?" La chaine ''p'' pourrait être une "petite" chaine de quelques milliers de caractères, alors que la chaine ''S'' pourrait être une "grosse" chaine de plusieurs milliard de caractères. Lorsque la chaine ''S'' est fixe, cette recherche se fait en un temps proportionnel à la taille de ''p'', indépendamment de la taille de ''S'' ! Ce qui rend ceci possible est le précalcul de l'arbre des suffixes de ''S'', une fois pour toute. Si on fait ce précalcul de manière naïve, il prend un temps proportionnel à la taille de ''S'' '''au carré'''. Lorsque ''S'' contient des milliards de caractéres, ceci n'est pas raisonnable. |
|||
L'algorithme de Ukkonen permet de calculer l'arbre des suffixes en un temps proportionnel à la taille de ''S''. |
|||
'''Objectifs :''' |
|||
# comprendre la structure d'arbre des suffixes |
|||
# coder une version naïve du calcul de l'arbre des suffixes |
|||
# comprendre et coder une version de l'algorithme de Ukkonen, et comparer les temps de calcul |
|||
# si le temps le permet, comprendre l'algorithme SA-IS qui permet de construite le tableau des suffixes en un temps proportionnel à la taille de ''S''. |
|||
'''Référence :''' |
|||
# les [https://www.youtube.com/playlist?list=PL2mpR0RYFQsDFNyRsTNcWkFTHTkxWREeb vidéos de Ben Langmead] sur les arbres de suffixes (vidéos 1 -- 9) |
|||
# description de l'algoritme de Ukkonen dans Dan Gusfield, ''Algorithms on Strings, Trees and Sequences''. |
|||
=== [[Polyominos, pavages et solveurs SAT]] === |
|||
'''Tuteur :''' Pierre Hyvernat |
|||
'''Résumé :''' les polyominos sont, comme les pièces de Tetris, des assemblages de petits carrés collés par leurs bords. Un ensemble de polyomino ''pavent'' une forment lorsqu'on peut la remplir avec des ces polyominos, sans chevauchement et sans trou. Il existe des algorithmes spécifiques pour vérifier si on peut paver une forme, mais il est également possible de transformer la question en une grosse formule booléenne qui exprime que chaque case se retrouve bien recouverte, que chaque polyomino a bien la bonne forme, etc. On peut alors utiliser un ''solveur SAT'' qui cherche les solutions pour une telle formule. |
|||
En écrivant des formules un peu plus complexes, on peut essayer de calculer le nombre de [https://en.wikipedia.org/wiki/Heesch%27s_problem Heesch's problem] d'un polyomino. Il s'agit du nombre d'anneaux que l'on peut mettre autour d'un polyomino donné. Par exemple, la figure suivante montre un polyomino avec nombre de Heesh égal à 1 : le polyomino est entouré d'un anneau (composé de copies de lui même), et on ne peut pas ajouter de second anneau supplémentaire (sans chevauchement et sans trou). |
|||
[[File:heesch.png|200px]] |
|||
Le plus grand nombre de Heesh fini connu est ... 6 ! (Mais il n'est pas atteint par un polyomino.) |
|||
'''Objectifs :''' |
|||
# Comprendre l'utilisation d'un solveur SAT, par exemple en codant la résolution de sudoku. |
|||
# Coder (en Python ?) la génération de la formule associée à un problème de pavage, et la transformation d'une solution booléenne en image finale. |
|||
# Coder (en Python ?) la génération de la formule associée à la question "le nombre de Heesh de ce polyomino est au moins égal à H", et la transformation d'une solution en image finale. |
|||
'''Référence :''' |
|||
# <tt>TODO: ref sur les solveur SAT</tt> |
|||
# G. Kaplan, Heesch Numbers of Unmarked Polyforms : [https://isohedral.ca/heesch-numbers-of-unmarked-polyforms/ blog], [https://arxiv.org/pdf/2105.09438 article] |
|||
===Approximations d'Euler et Runge-Kutta pour la modélisation du problème à 3 corps=== |
|||
'''Tuteur :''' Mouloud Kessar |
|||
'''Résumé :''' |
|||
en astronomie, la modélisation du problème à N corp est un enjeu majeur. Il est indispensable pour l'exploration spatiale, notamment pour l'envoie de sonde sur Mars, ou |
|||
Titan (Lune de Jupiter). |
|||
Les équations décrivant le problème à N corps existent depuis de nombreuses années, mais les mathématiciens et les physiciens ne savent pas les résoudre analytiquement. |
|||
Des codes de calcul existent pour réaliser des simulations du système solaire. |
|||
D'un point de vue algorithmique, le point clef se situe dans l'approximation choisie pour les dérivées en temps. |
|||
Une approximation à l'aide d'une méthode type Euler ou Runge-Kutta va avoir un ordre de précision prédéfini. |
|||
Toutes ces approximations ne se valent pas, et une analyse rigoureuse de la fiabilité de ces méthodes est nécessaire. |
|||
'''Note :''' il n'est pas nécessaire de connaître les méthodes numériques au préalables car elles seront introduites et développées dans un cadre simple au fur et à mesure. |
|||
'''Objectifs :''' |
|||
* Comprendre le fonctionnement de l'approximation d'une dérivée par une méthode numérique (type Euler et Runge-Kutta d'ordre 2) |
|||
* Développer un programme permettant de prédire les mouvements des corps suivants: Jupiter, La Terre, et Le Soleil |
|||
* Mesurer l'ordre de précision des deux méthodes numériques implémentées, et comparer à l'ordre théorique. |
|||
* Si le temps le permet: |
|||
** Ajouter les schémas Runge-Kutta 4 et 6 |
|||
** modifier le code pour inclure Mars, Venus et Mercure |
|||
'''Références :''' |
|||
# La formulation générale du problème à N-corp est donnée ici: https://en.wikipedia.org/wiki/N-body_problem |
|||
# Ce type d'étude peut devenir autrement plus complexe que la version présentée ici. Dans le film "The Martian" , un astronaute est piégé sur Mars, et son équipe qui était en route pour la terre doit venir le récupérer. Le centre de calcul "Pléiades" de la NASA est présenté, et utilisé pour déterminer s'il est possible de renvoyer le vaisseau spatial récupérer l'astronaute, notamment à l'aide d'une fronde gravitationnelle. |
|||
=== [[Jeu de la vie]] === |
|||
'''Tuteur :''' Romain Negro |
|||
'''Résumé :''' Le [https://fr.wikipedia.org/wiki/Jeu_de_la_vie jeu de la vie] est un [https://fr.wikipedia.org/wiki/Automate_cellulaire automate cellulaire] inventé dans les années 70 par John Conway dont les |
|||
règles sont simples, mais dont des comportements macroscopiques complexes peuvent apparaître. Des simples structures immobiles aux structures semblant dotées d'intelligence, le jeu de la vie est |
|||
[https://fr.wikipedia.org/wiki/Turing-complet Turing-complet]. |
|||
Le jeu de la vie se présente ainsi : sur une grille infinie, il y a des cellules vivantes ou mortes. A chaque étape, chaque cellule naît, reste en vie ou meurt en fonction de son 8-voisinage. Une cellule naît si |
|||
exactement 3 de ses voisins sont vivants. Une cellule reste en vie son état si celle-ci a entre 2 et 3 voisins vivants. Dans les autres cas, la cellule meurt. |
|||
Afin de faire fonctionner cet automate, l'approche naïve consiste à chaque étape à calculer pour chaque cellule son état suivant. Cependant, celle-ci ne fonctionne que sur une grille finie et n'est pas très |
|||
efficace pour de plus grandes grilles. |
|||
Certaines approches permettent de travailler sur des grilles de taille infinie (en théorie), voire de pouvoir rapidement se déplacer de plusieurs étapes dans le temps. D'autres approches permettent même de |
|||
s'affranchir de la notion de grille et d'étapes. |
|||
'''Objectifs :''' |
|||
# implémenter (en Python ou Javascript) une version naïve du jeu de la vie sur une grille finie, |
|||
# proposer une implémentation permettant d'effectuer la simulation sur une grille infinie, |
|||
# comprendre et si le temps le permet implémenter la simulation en utilisant une approche en arbre. |
|||
# s'il reste encore du temps, comprendre comment fonctionne l'approche continue du jeu de la vie |
|||
'''Référence :''' |
|||
# Liens wikipédia cités dans le résumé |
|||
# [https://johnhw.github.io/hashlife/index.md.html Implémentation utilisant des arbres] |
|||
# [https://arxiv.org/pdf/2005.03742 Lenia : jeu de la vie "continu"] |
|||
===[[Programmation graphique sur GPU]]=== |
|||
'''Tuteur :''' Jacques Olivier Lachaud |
|||
'''Résumé et objectifs :''' les cartes graphiques modernes permettent l'affichage de millions de polygones avec des rendus presque réalistes en temps réel. |
|||
L'objectif de ce sujet est de découvrir la modélisation 3D, puis les programmations spécifiques des vertex et fragment shaders pour réaliser certains types d'effet (camera, |
|||
transformations géométriques, illumination, textures, halos, stylisations, incrustations). |
|||
Le pipeline OpenGL sera étudié, et accédé via WebGL/javascript/three.js. Dans une 2eme partie, certains shaders de shadertoy.com seront étudiés plus en détails, afin de |
|||
comprendre les nombreuses astuces utilisées par les experts du domaine pour faire des effets impressionnants en temps réel. |
|||
'''Remarque :''' sujet discuté avec Vetea Stoll |
|||
== sujets 2023-2024 == |
== sujets 2023-2024 == |
||
Dernière version du 18 décembre 2024 à 13:22
Responsable:
- 2017--2021 : Jacques-Olivier Lachaud
- 2022-- : Pierre Hyvernat
Ce module amène l'étudiant à effectuer des recherches bibliographiques sur un sujet donné, et à synthétiser ses résultats sous la forme d'un exposé construit.
L'étudiant, à partir d'un sujet et d'un ou plusieurs articles initiaux, doit approfondir le sujet, appréhender son historique, ses évolutions, et son état actuel.
A côté des ressources fournies par les bibliothèques, quelques pointeurs très utiles pour faire des recherches bibliographiques:
- Scholar Google (libre)
- ResearchGate (libre)
- MashSciNet (plus math)
- Springer (accès via USMB)
- Elsevier Sciencedirect (accès via USMB)
- SciHub lorsqu'on ne trouve pas
La synthèse bibliographique se fait en interaction avec le tuteur par des visites régulières et/ou des compte-rendus d'avancement par email. La synthèse finale fait l'objet d'un exposé final (15-20 minutes + questions) et d'un document de présentation.
sujets 2024-2025
Algorithmes de colorations de graphes
Tuteur : Valentin Gledel
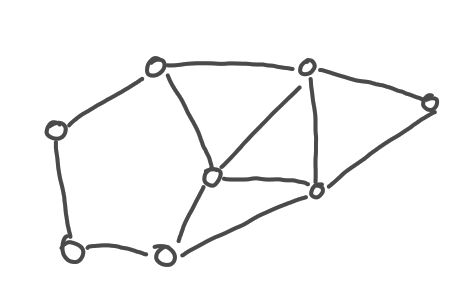
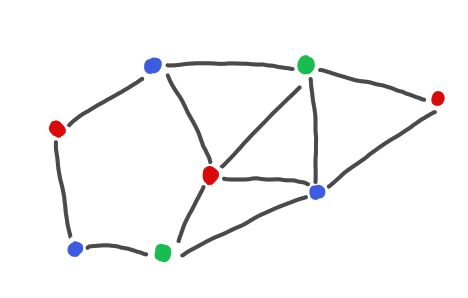
Résumé : Un graphe est un ensemble de sommets et un ensemble d’arêtes sur ces sommets. Une coloration propre d'un graphe est une assignation de couleurs à chaque sommet du graphe telle que chaque paire de sommets reliée par une arête a des couleurs différentes.
 |
 |
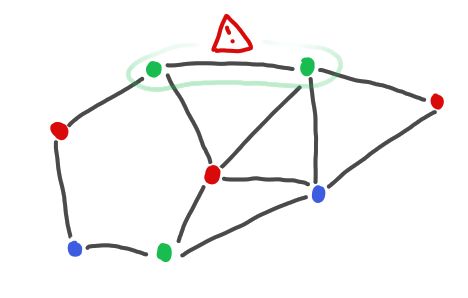 |
| Un graphe | Une coloration propre de ce graphe | Une coloration impropre du graphe |
Connaître le nombre minimum de couleurs permettant de colorer proprement un graphe est un problème NP-difficile. Cependant, il existe des algorithmes de coloration de graphe permettant de trouver une coloration propre en fonction du nombre de voisins maximums d'un sommet. L'objectif de ce sujet est d'implémenter certains de ces algorithmes.
Objectifs :
- implémenter l'algorithme de coloration glouton d'un graphe
- implémenter l'amélioration de cet algorithme en utilisant la dégénérescence du graphe
- implémenter l'algorithme issus du théorème de Brooks
- éventuellement, implémenter un algorithme de coloration d'arêtes
- éventuellement, implémenter un algorithme de transformation du problème SAT en problème de coloration
Algorithme de Ukkonen / algorithme SA-IS
Tuteur : Pierre Hyvernat
Résumé : L'arbre des suffixes est une structure de données qui permet de répondre très rapidement à de nombreuses requêtes du style "est-ce que la chaine p apparait dans la chaine S ?" La chaine p pourrait être une "petite" chaine de quelques milliers de caractères, alors que la chaine S pourrait être une "grosse" chaine de plusieurs milliard de caractères. Lorsque la chaine S est fixe, cette recherche se fait en un temps proportionnel à la taille de p, indépendamment de la taille de S ! Ce qui rend ceci possible est le précalcul de l'arbre des suffixes de S, une fois pour toute. Si on fait ce précalcul de manière naïve, il prend un temps proportionnel à la taille de S au carré. Lorsque S contient des milliards de caractéres, ceci n'est pas raisonnable.
L'algorithme de Ukkonen permet de calculer l'arbre des suffixes en un temps proportionnel à la taille de S.
Objectifs :
- comprendre la structure d'arbre des suffixes
- coder une version naïve du calcul de l'arbre des suffixes
- comprendre et coder une version de l'algorithme de Ukkonen, et comparer les temps de calcul
- si le temps le permet, comprendre l'algorithme SA-IS qui permet de construite le tableau des suffixes en un temps proportionnel à la taille de S.
Référence :
- les vidéos de Ben Langmead sur les arbres de suffixes (vidéos 1 -- 9)
- description de l'algoritme de Ukkonen dans Dan Gusfield, Algorithms on Strings, Trees and Sequences.
Polyominos, pavages et solveurs SAT
Tuteur : Pierre Hyvernat
Résumé : les polyominos sont, comme les pièces de Tetris, des assemblages de petits carrés collés par leurs bords. Un ensemble de polyomino pavent une forment lorsqu'on peut la remplir avec des ces polyominos, sans chevauchement et sans trou. Il existe des algorithmes spécifiques pour vérifier si on peut paver une forme, mais il est également possible de transformer la question en une grosse formule booléenne qui exprime que chaque case se retrouve bien recouverte, que chaque polyomino a bien la bonne forme, etc. On peut alors utiliser un solveur SAT qui cherche les solutions pour une telle formule.
En écrivant des formules un peu plus complexes, on peut essayer de calculer le nombre de Heesch's problem d'un polyomino. Il s'agit du nombre d'anneaux que l'on peut mettre autour d'un polyomino donné. Par exemple, la figure suivante montre un polyomino avec nombre de Heesh égal à 1 : le polyomino est entouré d'un anneau (composé de copies de lui même), et on ne peut pas ajouter de second anneau supplémentaire (sans chevauchement et sans trou).
Le plus grand nombre de Heesh fini connu est ... 6 ! (Mais il n'est pas atteint par un polyomino.)
Objectifs :
- Comprendre l'utilisation d'un solveur SAT, par exemple en codant la résolution de sudoku.
- Coder (en Python ?) la génération de la formule associée à un problème de pavage, et la transformation d'une solution booléenne en image finale.
- Coder (en Python ?) la génération de la formule associée à la question "le nombre de Heesh de ce polyomino est au moins égal à H", et la transformation d'une solution en image finale.
Référence :
Approximations d'Euler et Runge-Kutta pour la modélisation du problème à 3 corps
Tuteur : Mouloud Kessar
Résumé : en astronomie, la modélisation du problème à N corp est un enjeu majeur. Il est indispensable pour l'exploration spatiale, notamment pour l'envoie de sonde sur Mars, ou Titan (Lune de Jupiter).
Les équations décrivant le problème à N corps existent depuis de nombreuses années, mais les mathématiciens et les physiciens ne savent pas les résoudre analytiquement.
Des codes de calcul existent pour réaliser des simulations du système solaire.
D'un point de vue algorithmique, le point clef se situe dans l'approximation choisie pour les dérivées en temps.
Une approximation à l'aide d'une méthode type Euler ou Runge-Kutta va avoir un ordre de précision prédéfini.
Toutes ces approximations ne se valent pas, et une analyse rigoureuse de la fiabilité de ces méthodes est nécessaire.
Note : il n'est pas nécessaire de connaître les méthodes numériques au préalables car elles seront introduites et développées dans un cadre simple au fur et à mesure.
Objectifs :
- Comprendre le fonctionnement de l'approximation d'une dérivée par une méthode numérique (type Euler et Runge-Kutta d'ordre 2)
- Développer un programme permettant de prédire les mouvements des corps suivants: Jupiter, La Terre, et Le Soleil
- Mesurer l'ordre de précision des deux méthodes numériques implémentées, et comparer à l'ordre théorique.
- Si le temps le permet:
- Ajouter les schémas Runge-Kutta 4 et 6
- modifier le code pour inclure Mars, Venus et Mercure
Références :
- La formulation générale du problème à N-corp est donnée ici: https://en.wikipedia.org/wiki/N-body_problem
- Ce type d'étude peut devenir autrement plus complexe que la version présentée ici. Dans le film "The Martian" , un astronaute est piégé sur Mars, et son équipe qui était en route pour la terre doit venir le récupérer. Le centre de calcul "Pléiades" de la NASA est présenté, et utilisé pour déterminer s'il est possible de renvoyer le vaisseau spatial récupérer l'astronaute, notamment à l'aide d'une fronde gravitationnelle.
Jeu de la vie
Tuteur : Romain Negro
Résumé : Le jeu de la vie est un automate cellulaire inventé dans les années 70 par John Conway dont les règles sont simples, mais dont des comportements macroscopiques complexes peuvent apparaître. Des simples structures immobiles aux structures semblant dotées d'intelligence, le jeu de la vie est Turing-complet.
Le jeu de la vie se présente ainsi : sur une grille infinie, il y a des cellules vivantes ou mortes. A chaque étape, chaque cellule naît, reste en vie ou meurt en fonction de son 8-voisinage. Une cellule naît si exactement 3 de ses voisins sont vivants. Une cellule reste en vie son état si celle-ci a entre 2 et 3 voisins vivants. Dans les autres cas, la cellule meurt.
Afin de faire fonctionner cet automate, l'approche naïve consiste à chaque étape à calculer pour chaque cellule son état suivant. Cependant, celle-ci ne fonctionne que sur une grille finie et n'est pas très efficace pour de plus grandes grilles.
Certaines approches permettent de travailler sur des grilles de taille infinie (en théorie), voire de pouvoir rapidement se déplacer de plusieurs étapes dans le temps. D'autres approches permettent même de s'affranchir de la notion de grille et d'étapes.
Objectifs :
- implémenter (en Python ou Javascript) une version naïve du jeu de la vie sur une grille finie,
- proposer une implémentation permettant d'effectuer la simulation sur une grille infinie,
- comprendre et si le temps le permet implémenter la simulation en utilisant une approche en arbre.
- s'il reste encore du temps, comprendre comment fonctionne l'approche continue du jeu de la vie
Référence :
- Liens wikipédia cités dans le résumé
- Implémentation utilisant des arbres
- Lenia : jeu de la vie "continu"
Programmation graphique sur GPU
Tuteur : Jacques Olivier Lachaud
Résumé et objectifs : les cartes graphiques modernes permettent l'affichage de millions de polygones avec des rendus presque réalistes en temps réel. L'objectif de ce sujet est de découvrir la modélisation 3D, puis les programmations spécifiques des vertex et fragment shaders pour réaliser certains types d'effet (camera, transformations géométriques, illumination, textures, halos, stylisations, incrustations). Le pipeline OpenGL sera étudié, et accédé via WebGL/javascript/three.js. Dans une 2eme partie, certains shaders de shadertoy.com seront étudiés plus en détails, afin de comprendre les nombreuses astuces utilisées par les experts du domaine pour faire des effets impressionnants en temps réel.
Remarque : sujet discuté avec Vetea Stoll
sujets 2023-2024
Génération de labyrinthes "organiques"
Tuteur : Pierre Hyvernat
Résumé : la génération de labyrinthes est un problème classique, notamment abordé dans les cours d'algorithmes de graphes. Ces méthodes permettent de générer des labyrinthes sur des grilles, typiquement carrées :
 |
La création de labyrinthe "organiques", du style
 |
utilise une méthode très différente. Les détails sont décrits dans un article publié en 2006: http://www.dgp.toronto.edu/~karan/artexhibit/mazes.pdf. La description peut sembler très abstraite, mais l'idée initiale est assez simple : une courbe initiale est, petit à petit, déformée aléatoirement.
Objectif : comprendre la méthode de base, et l'implémenter pour générer des labyrinthes organiques. La première version pourra être codée en Python, mais comme la méthode nécessite une grosse quantité de calculs, il pourra être intéressant de coder une seconde version en utilisant un langage compilé si l'on souhaite obtenir de "gros" labyrinthes. De nombreuses améliorations sont décrites dans l'article de H. Pedersen et K. Singh, et il serait intéressant de d'en implémenter certaines, soient en Python (en les testant sur de petits labyrinthes) soit dans un autre langage.
Référence : Hans Pedersen et Karan Singh, Organic Labyrinths and Mazes, http://www.dgp.toronto.edu/~karan/artexhibit/mazes.pdf
Tramage artistique d'images
Tuteur : Jacques-Olivier Lachaud
Résumé : Le tramage d'une image (en anglais *dithering* ou *half-toning*) consiste à esquisser une image en niveaux de gris ou en couleur à l'aide de très peu d'encres ou couleurs différentes. Historiquement, l'utilisation la plus courante est en impression: un fax ne dispose que d'une encre noire (donc 2 couleurs noir et blanc pour transférer une image), les imprimantes n'ont que 4 encres (et donc cinq couleurs jaune, cyan, magenta, noir et le blanc du papier). Les premiers ordinateurs avaient des écrans avec très peu de couleurs, donc les photos étaient approchées avec 8 ou 16 couleurs.
En informatique, les algorithmes de tramage par diffusion d'erreur Floyd-Steinberg sont faciles à implémenter et rapide, donc très utilisés.
Néanmoins, il existe des algorithmes qui donnent des résultats beaucoup plus jolis, notamment celui proposé par Ostromoukhov et Hersch (1999). Nous proposons de l'étudier et de l'implémenter.
 |
 |
| Floyd-Steinberg | Ostromoukhov-Hersch |
Objectif : Comprendre les principes du tramage, éventuellement coder en python/opencv l'algorithme basique. Comprendre ensuite l'algorithme d'Ostromoukhov et Hersch (1999), et l'implémenter en python, d'abord en noir et blanc, et si le temps le permet, en couleur.
Références :
- Ostromoukhov et Hersch, Multi-Color and Artistic Dithering, ACM SIGGRAPH 1999
- OpenCV, pratique pour lire une image, l'afficher, faire des traitements.
Rendu réaliste de scènes 3D par lancer de rayons
Tuteur : Jacques-Olivier Lachaud
Note : Sujet demandé par Lukas Rey.
Résumé : Le rendu réaliste de scène 3D a été (et reste) un des objectifs majeurs de l'informatique graphique, notamment grâce à ses nombreuses applications dans différents domaines : le cinéma (effets spéciaux), mais aussi le marketing, la publicité, l'architecture, ou l'art. L'algorithme le plus utilisé est appelé "lancer de rayons", avec un objectif de simuler le trajet des rayons lumineux dans une scène 3D afin de déterminer les couleurs perçues par un observateur. Plutôt que de calculer tous les rayons lumineux d'une scène, cet algorithme calcule seulement le trajet inverse des rayons lumineux qui arrivent dans l'oeil de l'observateur, ce qui est beaucoup plus économique. On verra que cet algorithme permet de simuler des matériaux réfléchissants ou (semi-)transparents, de calculer des ombres portées, de simuler du brouillard...
Objectif : Il s'agit de comprendre d'où vient la couleur perçue d'un objet, d'implémenter l'algorithme récursif classique du lancé de rayons, au moins avec des objets simples (sphères, tétraèdres), et de voir comment optimiser les calculs (car ça devient vite coûteux). On pourra s'appuyer sur ce TP pour l'implémentation.
Références :
- https://en.wikipedia.org/wiki/Ray_tracing_(graphics)
- https://jacquesolivierlachaud.github.io/lectures/info804/Tests/html/ig_tp2.html
Rendu temps réel avec OpenGL
Tuteur : Colin Weill-Duflos
Résumé : On cherche à utiliser une API graphique (OpenGL) afin de faire du rendu de scène 3d en utilisant la carte graphique. Cela permet d'utiliser les techniques de rendu 3d en temps réel (rastérisation) et de les faire effectivement fonctionner en temps réel, permettant d'afficher une scène avec laquelle on peut intéragir : en déplaçant la caméré, en bougeant des éléments... Ces techniques ont déjà été utilisée dans des années précédentes, sans utiliser la carte graphique (le résultat était assez lent). Grâce à OpenGL, la plupart de ces opérations peuvent s'effectuer sur la carte graphique, ce qui permet de ne pas avoir à en recoder une partie (grâce à des composants capables de faire uniquement ces opérations) et d'être plus rapide.
Objectifs :
- comprendre les techniques de raterisation
- comprendre la pipeline OpenGL
- implémenter une scène avec un objet et une caméra controlable
- rajouter des shaders pour simuler la lumière (Phong shading), variantes stylisées (Toon shading)
- rajouter des textures sur la scène
- faire des shadow maps pour les ombres
Références :
- [Travaux précédents](http://os-vps418.infomaniak.ch:1250/mediawiki/images/0/0d/Gossin-2023.pdf)
- [Pipeline OpenGL](https://www.khronos.org/opengl/wiki/Rendering_Pipeline_Overview)
- [Modèle d'illumination](https://fr.wikipedia.org/wiki/Ombrage_de_Phong)
- [Toon shading](https://fr.wikipedia.org/wiki/Ombrage_de_cellulo%C3%AFd)
- [Shadow maps](https://learnopengl.com/Advanced-Lighting/Shadows/Shadow-Mapping)
Problèmes indécidables
Tuteur : Sébastien Tavenas
Résumé : Quand on a un calcul à faire, on peut se demander de la meilleure implémentation pour faire faire ce calcul par un ordinateur. On pense généralement moins à la question - pourtant primordiale - de savoir si ce calcul peut être effectué par l’ordinateur. Pourtant, on sait depuis l’origine de l’informatique qu’il existe des fonctions que l’on ne peut pas calculer à l’aide d’un ordinateur. On cherchera à comprendre ce que serait un programme qui résoudrait le problème de l’arrêt et pourquoi, il ne marchera pas. On pourra se demander alors s’il y a un lien entre les différents problèmes non-calculables : avec une librairie qui résout le problème de l’arrêt, peut-on écrire un problème qui résout le problème de correspondance de Post ? Peut-on imaginer un problème qu’on ne pourrait pas résoudre même si on avait une fonction qui résolvait le problème de l’arrêt ?
Objectif : Comprendre la notion de fonction calculable (et donc de fonction non-calculable). Donner des exemples. "Coder" l’argument diagonal de la non-calculabilité de l’arrêt. Coder une réduction entre deux problèmes non-calculables.
Références :
- Wikipédia - Théorie de la calculabilité
- Wikipédia - Problème de l'arrêt
- Livre récent en français sur la théorie de la calculabilité
Réseaux de neurones et apprentissage
Tuteur : François Boussion
Note : sujet demandé par Elliot Moiroud
Résumé :
Objectif :
- se familiariser avec les concepts utilisés en apprentissage,
- essayer d'implémenter une version ultra simple de la procédure d'apprentissage,
- utiliser une bibliothèque existante sur quelques exemples.
Références :
Synchronisation dans les Systèmes Distribués
Tuteur : François Boussion
Résumé : l'algorithme de Lamport joue un rôle crucial dans la synchronisation des horloges dans un réseau de machines qui ne sont pas nécessairement précises ou synchronisées entre elles. Il permet de créer un consensus sur l'ordre des événements dans un système distribué, où la communication peut être retardée ou désordonnée. Cette capacité est fondamentale pour assurer la cohérence et la fiabilité des opérations dans des environnements distribués, tels que les bases de données distribuées, les systèmes de fichiers en réseau et les applications de blockchain. Après avoir maîtrisé l'algorithme de Lamport, l'étudiant pourra les fautes byzantines pour comprendre comment les systèmes distribués gèrent les informations contradictoires ou erronées transmises par différents nœuds du réseau.
Objectif :
- Analyser et comprendre l'algorithme de Lamport pour la synchronisation des horloges.
- (Examiner les fautes byzantines et leur influence sur la stabilité des systèmes distribués.)
Référence :
Time, Clocks, and the Ordering of Events in a Distributed System. https://lamport.azurewebsites.net/pubs/time-clocks.pdf
Programmation dynamique et complexité
Tuteur : Tom Hirschowitz
Résumé : La programmation dynamique est sans doute une des techniques de programmation qui porte le plus mal son nom. Elle s'applique lorsqu'un problème peut se décomposer en sous-problèmes, dont les solutions peuvent être combinées. Dans le cas relativement simples où les sous-problèmes sont toujours disjoint, on utilise une approche de type "diviser pour rêgner". Lorsque ce n'est pas le cas, il faut faire attention à ne pas dupliquer les calculs. Les deux approches habituelles sont :
- la "mémoization", qui consiste à sauvegarder toutes les solutions trouvées pour éviter de les recalculer,
- la "programmation dynamique" qui consiste à faire les solutions dans le "bon ordre" afin de ne jamais avoir besoin d'une solution qui n'aurait pas été calculée.
Ces techniques permettent en général d'obtenir un algorithme beaucoup plus rapide que la version naïve.
Objectif :
- étudier les méthodes de "mémoization" et "programmation dynamique" sur plusieurs exemples et les comparer
- mettre en évidence les complexités "pratiques" de ces algorithmes au moyen de benchmarks pertinents
- comprendre les calculs "théoriques" de la complexité de ces algorithmes pour vérifier que les prédictions correspondent à la pratique.
Référence :
- "Introduction à l'algorithmique", T. Cormen, C. Leiserson, R. Rivest, C. Stein
- la page wikipedia française : https://fr.wikipedia.org/wiki/Programmation_dynamique
sujets 2022-2023
algorithmes de recherche de chaines
- Tuteur : Pierre Hyvernat
- Résumé : rechercher si une chaine s1 apparait à l'intérieur d'une chaine s2 est assez simple, mais l'algorithme naïf n'est pas très rapide. L'objectif de ce sujet est de s'intéresser à certains algorithmes de recherche de sous-chaines plus efficaces. Le plus simple est probablement l'algorithme KMP (du noms de ses inventeurs : Knuth, Morris et Pratt) qui évite des comparaisons inutiles de l'algorithme naïf. L'algorithme de Boyer-Moore utilise des idées similaires mais considère la sous-chaine (s1) à l'envers, ce qui lui permet d'aller en général plus vite. Ces algorithmes restent assez lents lorsque la chaine s2 est très grande. C'est par exemple le cas en bio-informatique lorsque l'on doit rechercher des chaines dans le génome. Dans ce cas, la chaine s2 est fixe et on rercherche de nombreuses sous-chaines s1. Il est alors possible de faire un pré-traitement pour faire une recherche beaucoup plus rapide qui ne dépend pas de la taille de s2 !
- Objectif :
- comprendre le fonctionnement de quelques uns de ces algorithmes
- les implémenter (par exemple en Python)
- essayer de les comparer
- Liens utiles :
- https://en.wikipedia.org/wiki/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm
- https://en.wikipedia.org/wiki/Boyer%E2%80%93Moore_string-search_algorithm
- https://en.wikipedia.org/wiki/Aho%E2%80%93Corasick_algorithm
- transformé de Burrows-Wheeler et recherche de sous-chaines https://www.youtube.com/watch?v=P3ORBMon8aw
génération de labyrinthes
- Tuteur : Pierre Hyvernat
- Résumé : il existe de nombreuses méthodes algorithmiques pour générer des labyrinthes aléatoires. La plupart de ces méthodes sont expliquées sur des grilles carrées mais il est possible de les implémenter sur d'autres types de grilles. Il est possible des les adapter par exemple pour générer des labyrinthes circulaires, cylindriques, ou sphériques ; ou bien des labyrinthes en plusieurs parties (de grandes pièces contenant des labyrinthes, reliées par des couloirs formant un autre labyrinthe).
- Objectif :
- comprendre le fonctionnement de plusieurs algorithmes de génération de labyrinthes
- les étendres à des grilles plus intéressantes
- expérimenter et chercher des manières simples de générer un labyrinthe "continu" (La solution décrite dans "How to Generate Perfect Mazes?" est probablement un peu trop complexe.)
- Liens utiles
- le livre "Mazes for programmers", https://pragprog.com/titles/jbmaze/mazes-for-programmers/
- l'article "How to Generate Perfect Mazes?", https://hal.uca.fr/hal-03174952/file/article-journal-2020.pdf
- l'article "Organic Labyrinths and Mazes", http://www.dgp.toronto.edu/~karan/artexhibit/mazes.pdf
L’infâme GOTO
- Tuteur : François Boussion
- Résumé : L’instruction goto n’a aujourd’hui plus la côte parmi les informaticiens, et est souvent considérée comme une instruction à bannir. L'idée est d'explorer ce que permet cette instruction, et comment a évolué son utilisation.
- Objectifs :
- remplacer des structures de contrôles simples simples par des goto
- faire un programme plus complexe utilisant un maximum de goto
- expliquer l'évolution de l'utilisation du goto
- avantages/inconvénients de son utilisation
- comparaison des langages prenant en charge ou non cette instruction et pourquoi
- utilisation actuelle
Blockchains
- Tuteur : François Boussion
- Résumé : les blockchains sont de plus en plus populaires, utilisées initialement pour les cryptomonnaies, elles peuvent être utilisées pour stocker des données, gérer les contrats intelligents, etc.
- Objectifs :
- comprendre le fonctionnement des blockchains (par exemple avec l'article de Satoshi Nakamoto)
- implémenter une blockchaine
- ...
- Liens utiles :
Algorithmes de reconstruction de surfaces à partir d'images 3D
- Tuteur : Jacques-Olivier Lachaud
- Résumé : Les images 3D sont devenues courantes avec les outils d'acquisition comme les scanners X ou les scanners IRM. On peut aussi modéliser des objets 3D sous forme de volumes, pour ensuite en extraire des surfaces (e.g. modélisation de fluides, de feu ou de fumées). Un enjeu est de pouvoir construire des surfaces qui représentent le bord d'objets d'intérêt dans ces données volumiques. Les algorithmes les plus classiques reconstruisent une surface composée de triangles qui approchent un niveau de gris donné dans le volume 3D : c'est une iso-surface, comparable à une courbe d'iso-altitude dans une carte topographique, mais en 3D ! On s'intéreressera à deux algorithmes particulièrement : le marching-tetrahedra et le marching-cubes.
- Objectifs:
- Comprendre ce qu'est une iso-surface dans une image 3D ou dans une fonction implicite.
- Comprendre les points communs et différences des algorithmes Marching Tetrahedra et Marching Cubes
- Implémenter un des deux algorithmes. On utilisera Polyscope pour visualiser les surfaces en 3D avec python.
- On lira des fichiers .vol pour les images 3D, qui vous seront fournies.
- Liens utiles
 |
 |
| Coupes dans une image 3D | Isosurface dans cette image |
Invitation à la complexité algorithmique
- Tuteur : Tom Hirschowitz
- Résumé : on abordera le thème de la complexité algorithmique : étant donné un programme implémentant une fonction, peut-on borner son temps de calcul en fonction de la taille de ses entrées. On procédera par l'exemple, en tentant de confirmer la théorie par des expériences concrets de petits programmes (par exemple en Python). Comme point d'entrée, on pourra par exemple examiner les différences de complexité entre quelques algorithmes de tri.
- Objectifs :
- comprendre l'intérêt de la complexités "à un facteur de proportionalité près",
- se familiariser avec les notions et notations utilisées pour décrire la complexité en temps de calcul (ou en mémoire) des algorithmes,
- apprendre à vers de "benchmarks" pour évaluer l'efficacité réelle d'une fonction dans un langage de programmation,
- comprendre les limites de la complexités "à un facteur de proportionalité près".
sujets 2021-2022
Rust et la notion d'appartenance ("ownership")
- Présentation : Théo Connetable : Fichier:VISI401-2022-Connetable.pdf
- Tuteur : Pierre Hyvernat
- Résumé : dans la plupart des langages "haut niveau" (Python, Java, Javascript, ...), la mémoire est gérée automatiquement. Par exemple, Python détecte qu'une liste ne sert plus à rien pour libérer la mémoire qu'elle occupait. Dans les langages "bas niveau" (C), c'est au programmeur de libérer explicitement la mémoire qu'il utilise. (S'il ne le fait pas, son programme risque d'avoir des "fuites de mémoire".) Rust est un nouveau (première version en 2010) langage de programmation. Un des objectifs de Rust est d'offrir des garanties de sécurité sur la mémoire avec la notion d'appartenance. Ces garanties sont testées à la compilation et ne dégradent donc pas l'efficacité du programme final.
- Objectifs : l'objectif, après s'être familiarisé avec le langage Rust, est de comprendre à quoi correspond la notion de "ownership" ("appartenance") et de l'illustrer sur quelques exemples. Si l'étudiant ne les connait pas, les notions de pointeurs (en C), d'allocation sur la pile, sur le tas, et le concept de "ramasse miettes" (garbage collector" en anglais) seront des étapes préliminaires importantes.
- Références : pour commencer
- The Rust Programming Language https://doc.rust-lang.org/book/title-page.html, avec en particulier la section 4, "Understanding Ownership"
- Safe Systems Programming in Rust https://cacm.acm.org/magazines/2021/4/251364-safe-systems-programming-in-rust/fulltext
- Rust Ownership by Example https://depth-first.com/articles/2020/01/27/rust-ownership-by-example/
Bitcoin & blockchain
- Présentation : Baptiste Griva Fichier:VISI401-2022-Griva.pdf
- Tuteur : François Boussion
- Résumé : Les blockchain sont de plus en plus populaires. Avec l'article de Satoshi Nakamoto, l'étudiant devra comprendre son fonctionnement. On pourra dans un second temps s'intéresser aux attaques habituelles face à une blockchain.
- Objectifs:
- Comprendre le fonctionnement de la blockchain bitcoin
- S'intéresser à ses vulnérabilités (51% attack,...)
- Références: pour commencer https://bitcoin.org/bitcoin.pdf
Débruitage d'image
- Présentation : Lucas Policastro Fichier:VISI401-2022-Policastro.pdf
- Tuteur : Jacques-Olivier Lachaud
- Résumé : La plupart des procédés d'acquisition d'image (typiquement capteurs CCD ou CMOS des caméras ou téléphones) ne sont pas parfaits et introduisent du bruit (des perturbations) dans les images résultantes. Ce bruit ressemble en général à une perturbation aléatoire locale par capteur, indépendante de ce qui se passe sur un capteur proche. Peut-on alors améliorer la qualité visuelle d'une photo dégradée par un tel bruit (typiquement gaussien) ? On regardera notamment les algorithmes basées sur la variation totale et sur les moyennes non locales.
- Objectifs:
- Comprendre les algorithmes basées sur la variation totale et sur les moyennes non locales.
- On pourra s'appuyer sur les démos IPOL en ligne de ces algorithmes et leur description. http://www.ipol.im/pub/art/2011/bcm_nlm/
- L'algorithme des moyennes non locales est implémentable relativement facilement (même en numpy).
- Références:
- http://www.ipol.im/pub/art/2011/bcm_nlm/
- Le site https://www.ipol.im contient plein d'algos de restauration d'image (suivre Enhancement & Restoration, puis Denoising).
Sécurité des cartes RFID : le cas Mifare
- Présentation : Paul Aubry Fichier:VISI401-2022-Aubry.pdf
- Tuteur : Pierre Hyvernat
- Résumé : les cartes RFID (Radio Frequency IDentification) sont des cartes à puce qui peuvent communiquer avec un lecteur distant (mais proche). De nombreuses cartes de transport en commun ou d'ouverture de portes utilisent cette technologie. La carte Mifare classic, très répandue, utilise un protocole cryptographique pour éviter les "replay attacks" (enregistrer un échange pour le réutiliser) et le clonage de la carte. Le détails du protocole est longtemps resté un secret industriel, mais ceci n'a pas empéché la découverte de *grosses* failles. Il est maintenant possible de cloner une carte Mifare en quelques secondes avec du matériel grand public.
- Objectifs :
- comprendre fonctionne la protection contre les "replay attacks" à partir de challenges cryptographiques
- comprendre le protocole Mifare classic
- comprendre les attaques sur le protocole
- expérimenter avec des puces RFID existante *(facultatif)*
- regarder les évolutions du protocole pour se protéger de ces attaques
- Référence : F. D. Garcia, P. van Rossum, R. Verdult, R. Wichers Schreur : "Wirelessly Pickpocketing a Mifare Classic Card" https://www.cs.ru.nl/~flaviog/publications/Pickpocketing.Mifare.pdf
Ingénierie Dirigée par les Modèles (IDM)
- Présentation : Alexandre Desbos Fichier:VISI-401-2022-Desbos.pdf
- Tuteur : Philippe Pernelle
- Résumé : l'ingénierie dirigée par les modèles (ou MDE Model Driven Engineering) est une approche de conception basée sur la transformation de modèle sur des niveaux d'abstraction différents (modèle, méta-modèle, méta-méta-modèle ...). l'OMG propose une approche MDE basée sur 3 niveaux d'abstraction (CIM,PIM, PSM) permettant de bâtir une application en partant du niveaux d'abstraction le plus haut (CIM) et en procédant par transformation / raffinement pour arriver au PSM puis à la génération de code. Il existe par ailleurs différents langages (ATL, OCL) qui vont faciliter la transformation de modèle. A noter que la fondation Eclipse propose un environnement spécifique pour manipuler des modèles avec des implémentations d'ATL et d'OCL
- Objectifs : L'objectif est d'étudier ces mécanismes de transformation / raffinement par l'implémentation d'un cas d'étude dans eclipse en utilisant les langages ATL et OCL. Après une étude bibliographique des principes de MDA, l'idée est de mettre en oeuvre dans Eclipse des extrait des modèles CIM, PIM et PSM proposés par les articles ci-dessous puis d'essayer de construire des OCL et des scripts ATL afin de faciliter la transformation (sans aller jusqu'à la génération de code)
- Références : pour commencer
- These : https://hal.archives-ouvertes.fr/tel-01247610 (uniquement les pages 35 à 47)
- Models and Mechanisms for implementing playful scenarios https://hal.archives-ouvertes.fr/hal-01372311
- Digital Twin and Ecological Transition Integration in Training Process https://hal.archives-ouvertes.fr/hal-03375508
- Eclipse Modeling Tools https://www.eclipse.org/downloads/packages/release/2021-12/r/eclipse-modeling-tools
Couvrir un polygone rectilinéaire avec des rectangles
- Présentation : Maxent Bernier Fichier:VISI401-2022-Bernier.pdf
- Tuteur : Sébastien Tavenas
- Résumé : Un polygone est dit rectilinéaire si les seuls angles qui apparaissent sont des angles droits. On considérera des polygones simples (i.e., sans trous et qui ne s'auto-intersectent pas). Un tel polygone peut donc être recouvert par des carrés ou par des rectangles. On cherchera à écrire un algorithme qui trouve une couverture minimale (i.e., avec le moins de carrés/rectangles possibles). Dans le cas des carrés, on va pouvoir trouver un algorithme efficace pour ce problème. Malheureusement, le cas de la couverture minimale par les rectangles est NP-complète.
- Objectifs :
- Implémenter un algorithme de recouvrement par des carrés
- Comprendre ce qu'est un problème NP-complet et le lien avec la couverture par les rectangles
- Contourner la difficulté de la NP-complétude (heuristique ou cas des polygones orthogonalement convexes)
- Liens pour démarrer
Automates cellulaires
- Présentation : Emilien Boitouzet Fichier:VISI401-2022-Boitouzet.pdf
- Tuteur : Gérald Cavallini
- Sujet : La théorie des automates cellulaires est relativement simple, une série de règles permet de modifier l’état spatial et temporel d’une cellule en fonction de son voisinage. Cette théorie se décline en de nombreux cas d’étude, automate circulaire cyclique, 2D, 3D … En théorie, les automates cellulaires permettent aussi de réaliser des calculs. Cependant les réalisations pratiques manquent, ce sujet se propose d’étudier l’utilisation des automates cellulaires dans les domaines suivant par exemple :
- Modélisation des systèmes complexes (propagation des feux de forêt, processus de percolation, écoulement du sable ...)
- Modélisation du comportement d'un gaz
- Système dynamique discret alternatif au modèle physique des équations aux dérivées partielles
- Modélisation de la croissance de tissus cellulaires en biologie
- Simulation de la croissance des cristaux
- Correction automatique d’erreurs en imagerie
- Référence: https://mathworld.wolfram.com/CellularAutomaton.html
Programmation bare-metal
- Présentation : Andrien Montmayeur Fichier:VISI401-2022-Montmayeur.pdf
- Tuteur : Colin Weill-Duflos
- Sujet : l'execution d'un programme compilé peut parfois paraître un peu magique: on ne comprend pas forcément tout ce que fait le compilateur, et le système d'exploitation fournit des abstractions bien pratiques. Comment se débrouille-t-on dans un contexte où il n'y a pas de système d'exploitation, comme certaines applications embarquées ou bien le système d'exploitation lui-même?
- Objectifs : comprendre en détails la chaîne de compilation du C, l'architecture d'un executable et comment ce dernier est executé par une machine pour parvenir à faire executer un programme directement par un microprocesseur arm et interagir avec des périphériques simples.
- Référence:
- Architecture d'un executable
- les étapes de compilation du C (regarder notamment le linkage)
- débuter avec l'assembleur arm
GeoGebra et algèbre géométrique
- Présentation : Nolann Sanmarti Fichier:VISI401-2022-Sanmarti.pdf
- Tuteur : Stéphane Breuils
- Sujet : l'algèbre géométrique émerge récemment comme un outil prometteur pour la synthèse d'images : avec des points de contrôle, un produit, il est possible de représenter et de manipuler de manière efficace un ensemble d'objets géométriques. Récemment, des bibliothèques c++ ont été développées. Ces bibliothèques autorisent une utilisation générique de l'algèbre géométrique mais sont encore limitées par le manque d'outils intéractifs adaptés. Par ailleurs, le logiciel de visualisation GeoGebra est un outil particulièrement utile pour la visualisation et la résolution de problèmes géométriques. Le but de ce projet serait de travailler un binding entre l'algèbre géométrique et GeoGebra.
- Objectifs :
- se familiariser avec l'algèbre géométrique, et l'applet Javascript de GeoGebra,
- identifier les objets et les opérations géométriques intéressantes à visualiser avec l'algèbre géométrique,
- implantations d'une méthode générique permettant de générer des scripts dans l'applet Javascript de GeoGebra.
- Références :
- Projective geometric algebra: A new framework for doing euclidean geometry, Charles G. Gunn, 2019
- geogebra
sujets 2020-2021
Comment Facebook gère ses données ?
- Tuteur : François Boussion
- Résumé : Pour une base de données, il est impossible d'être cohérent, disponible tout le temps et partitionné. C'est le fameux théorème CAP. Pour autant, les données de Facebook sont cohérentes, disponibles tout le temps, et réparties à travers le monde !? Impossible. Pour l'étudiant, il faudra comprendre pourquoi c'est impossible, et comment Facebook fait en pratique pour gérer ce problème.
- Objectifs :
- Comprendre le CAP théorème, et sa démonstration
- Comprendre comment Facebook gère ce problème, et ses données d'une manière générale
- À définir, selon les questions que se pose l'étudiant.
- Références :
- Théorème CAP :
- https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_CAP
- Brewer's Conjeture and the Feasibility of Consistent, Available, Partition-Tolerant Web Services (https://awoc.wolski.fi/dlib/big-data/GiLy02-CAP.pdf)
- Facebook Social Graph :
- TAO : The power of the graph (https://engineering.fb.com/2013/06/25/core-data/tao-the-power-of-the-graph/)
- TAO: Facebook’s Distributed Data Store for the Social Graph (https://www.usenix.org/system/files/conference/atc13/atc13-bronson.pdf)
- Théorème CAP :
Algorithmes de calcul de l'enveloppe convexe
- Tuteur : Jacques-Olivier Lachaud
- Résumé : Les ensembles convexes ont beaucoup de propriétés géométriques intéressantes, par exemple détecter la collision de deux ensembles convexes est "facile" algorithmiquement. Une étape fréquente dans beaucoup d'algorithmes de traitements de données 2D/3D/nD est donc de calculer l'enveloppe convexe d'un nuage de points, c'est-à-dire le plus petit ensemble convexe contenant ces points. Il existe de nombreux algorithmes de calcul d'enveloppe convexe en 2D (Graham scan, Melkman, balayage de ligne (sweep-line), division-fusion, Chan's algorithm, Quickhull) et 3D (Chan's algorithm, Quickhull) et même nD (Quickhull notamment).

| Enveloppe convexe des points à coordonnées entières inclus dans une boule de diamètre 25 |
- Objectifs: il s'agira de regarder quelques uns de ces algorithmes, d'identifier leurs principales différences ainsi que leurs complexités théoriques et pratiques. On pourra aussi regarder plus précisément l'algorithme Quickhull, dont l'implémentation 2D est facile, et 3D accessible.
- Bibliographie initiale :
- Barber, C. B., Dobkin, D. P., & Huhdanpaa, H. (1996). The quickhull algorithm for convex hulls. ACM Transactions on Mathematical Software (TOMS), 22(4), 469-483 [(PDF)]
- [Algorithme de Graham (Wikipedia)]
- [Convex hull algorithms (Wikipedia)]
Algorithmes autour des polyominos
- Tuteur : Pierre Hyvernat
- Résumé : Un polyomino est une forme (sans trou) obtenue en collant des petits carrés de taille 1 par leurs bords. Des exemples connus sont par exemples les pièces du jeu tetris : il s'agit de "tétramino", c'est à dire de polyomino formés de 4 carrés. Voici également les pentaminos, composés de 5 carrés :
Une question récurrente est celle de la pavabilité : peut-on (en utilisant certains types de polyominos) paver un domaine donné. Lorsque le domaine est fini, on peut utiliser une recherche exhaustive, mais lorsqu'on veut paver tout le plan, le problème devient indécidable en général. Nous nous intéresserons au cas le plus simple : est-il possible de paver le plan tout entier en utilisant des polyominos tous identiques, et en utilisant uniquement des translations.
- Objectifs
- comprendre les définitions et notions de bases des polyominos, et en particulier leur représentation comme mot de contour
- implémenter différents algorithmes de reconnaissance de polyominos en Python
- comprendre la caractérisation des polyominos "exacts", càd ceux qui pavent le plan
- implémenter différents algorithmes de reconnaissance des polyominos exacts en Python
- Bibliographie initiale
- "Combinatoire des mots, géométrie discrète et pavages", Xavier Provencal (chapitres 1 et 2)
- "An algorithm for deciding if a polyomino tiles the plane by translation", Ian Gambini et Laurent Vuillon
Version algorithmique du lemme local de Lovász
- Tuteur : Sébastien Tavenas
- Résumé : Considérons un problème standard sur le routage de paquets dans des réseaux. Donnés un réseau et une collection de paquets, chacun venant avec un chemin dans le réseau (de la source vers la destination), le but est d’établir un planning qui minimise le temps pour que tous les paquets atteignent leur destination. Il est naturel de mesurer la qualité d’un tel planning en fonction de deux paramètres : la congestion c qui est le nombre maximum de paquets qui doivent emprunter une même arête du réseau et la dilatation d qui est le nombre maximum d’arêtes d’un chemin. En effet, il est facile de trouver un planning en temps c*d, et tout planning doit prendre comme temps au moins max(c,d).
En 1994, Leighton, Maggsand et Rao ont montré qu’il existait toujours un planning en temps O(c+d). Malheureusement, ce résultat est basé sur le lemme local de Lovász. Il s’agit d’un résultat classique de combinatoire dont la preuve était à l’époque non constructive. Le problème précédent du routage de paquets n’est qu’une application de ce lemme parmi tant d’autres. En 2010, Moser et Tardos donnèrent un algorithme (en plus assez simple et efficace) pour le lemme local de Lovász.
- Objectifs :
- Comprendre le lemme local de Lovász et certaines de ses applications
- Coder la version algorithmique de Moser et Tardos
- Coder des applications du lemme (comme par exemple le routage de paquets)
- Bibliographie initiale :
travaux réalisés 2019-2020
- Crypto-système de Merkle-Hellman et algorithme de Shamir, Ewan Rakotoanosy (Tuteur : Pierre Hyvernat)
- Reconstruction de surfaces à partir de nuages de points et de normales, Yohan Thépaut (Tuteur : Jacques-Olivier Lachaud)
- Algorithmes de super-résolution par apprentissage, Romain Théodet (Tuteur : Jacques-Olivier Lachaud)
- Autour de la question de la sensibilité des fonctions Booléennes, Christophe Carmagnac (Tuteur : Sébastien Tavenas)
- Structures de données purement fonctionnelles, Loïc Dornel (Tuteur : Tom Hirschowitz)
- Automates cellulaires et décidabilité, Lucas Chardonnet (Tuteur : François Boussion)
sujets 2019-2020
Crypto-système de Merkle-Hellman et algorithme de Shamir
- Tuteur : Pierre Hyvernat
- Résumé : Le système de Merkle-Hellman est un système cryptographique de type "clé publique / clé privée". Il a été inventé juste en 1978, après le système RSA (encore utilisé). Ce système a l'avantage d'être un peu plus simple, mais le **gros** désavantage d'avoir été craqué par A. Shamir en 1984. L'objectif est de comprendre le système, et la faille qu'il contenait. Cela permettra de comprendre l'algorithme de Shamir...
- Bibliographie initiale :
- Shamir, Adi (1984). "A polynomial-time algorithm for breaking the basic Merkle - Hellman cryptosystem". IEEE Transactions on Information Theory. 30 (5): 699–704. doi:10.1109/SFCS.1982.5 [PDF]
Reconstruction de surfaces à partir de nuages de points et de normales
- Tuteur : Jacques-Olivier Lachaud
- Résumé : Les lasers d'acquisition de données 3d permettent de fabriquer des données qui approchent le bord d'un objet 3D. Ces données sont souvent sous la forme d'un nuage de points, doublé d'un vecteur associé à chaque point et qui indique la direction normale à la surface de l'objet. On parle de données de Hermite. Il existe des algorithmes dédiés, très efficaces et robustes, pour reconstruire une surface qui passe par ces points. L'objectif est de comprendre les deux principales méthodes, l'une appelée reconstruction de Poisson, l'autre relié à la notion d'indice (ou winding number), leurs qualités et leur défaut.
- Bibliographie initiale:
- KAZHDAN, Michael, BOLITHO, Matthew, et HOPPE, Hugues. Poisson surface reconstruction. In : Proceedings of the fourth Eurographics symposium on Geometry processing. 2006 [PDF]
- BARILL, Gavin, DICKSON, Neil G., SCHMIDT, Ryan, et al. Fast winding numbers for soups and clouds. ACM Transactions on Graphics (TOG), 2018, vol. 37, no 4, p. 43. [[1]]
Algorithmes de super-résolution par apprentissage
- Tuteur : Jacques-Olivier Lachaud
- Résumé : La super-résolution consiste à, étant donné une image M x N, de fabriquer une image "zoomée" de taille kM x kN, où l'information inventée est "crédible". Le problème est évidemment mal posé mathématiquement, et du coup on rajoute de l'information a priori : continuité des couleurs, continuité des structures géométriques, modèles probabilistes, moyennes non-locales (auto-similarités), etc. Avec l'avènement du deep learning, des méthodes à base d'apprentissage ont vu le jour. En gros, un réseau de neurones (CNN) apprend sur plein d'images en "dézoomant" les images en entrées (facile, on sous-échantillonne), puis on utilise la fonction construite pour faire la super-résolution.
- L'objectif est de regarder les méthodes de super-résolution, notamment celles par apprentissage et de voir leurs qualités et défauts. On pourra aussi les comparer avec des méthodes purement géométriques de super-résolution, ou des méthodes de moyennes non-locales.
- Ce sujet a été discuté avec Romain Théodet et conduit à un stage au LAMA pour combiner méthode géométrique et méthode par deep learning pour la super-résolution.
- Bibliographie initiale :
- SHI, Wenzhe, CABALLERO, Jose, HUSZÁR, Ferenc, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In : Proceedings of the IEEE conference on computer vision and pattern recognition. 2016. p. 1874-1883 [PDF]?
- Lachaud, J.-O. and Kerautret, B., Geometric Total Variation for image vectorization, zooming and pixel art depixelizing, In : Proceedings of 5th Asian Conference on Pattern Recognition, 2019 Fichier:Paper-GTV.pdf
- [Démos en ligne d'algorithmes de super-résolution]
Autour de la question de la sensibilité des fonctions Booléennes
- Tuteur : Sébastien Tavenas
- Résumé : On souhaite s’intéresser aux problèmes résolus par des algorithmes qui répondent par Vrai/Faux. Ces problèmes ont des entrées dans {0,1}^n (entrées codées en binaire) et une sortie dans {0,1) (Vrai ou Faux). Il est donc naturel de s’intéresser aux propriétés de ces fonctions Booléennes. Un certain nombre de paramètres intéressants ont été identifiés, comme la complexité du certificat (nombre minimal de bits nécessaires pour connaître la valeur de sortie), le degré (degré d’un polynôme qui correspond à la fonction sur les entrées Booléennes), la sensibilité (lnombre de bits qui, s’ils sont modifiés, impliquent une modification de la sortie), et bien d’autres (taille d’un arbre de décision, complexité en requêtes classiques ou quantiques, taille des coefficients de Fourier,…). En 1992, Nisan et Szegedy ont montré que tous ces paramètres sont reliés entre eux : si on connait l’un d’eux, par exemple le degré, on sait alors que n’importe quel autre de ces paramètres, par exemple la taille de l’arbre de décision, est limité à un certain intervalle de valeurs. Tous, sauf un : la sensibilité. Aucune méthode de preuve semblait impliquer que ce paramètre ne pouvait pas être beaucoup plus petit que les autres. Nisan et Szegedy posèrent alors la question de savoir si la sensibilité d’une fonction Bolléenne était reliée ou non aux autres paramètres classiques.
- Cet été, en 2019, un chercheur, Hao Huang, a montré dans une preuve de deux pages que la sensibilité ne pouvait pas être significativement plus petite que les autres paramètres, résolvant le problème posé 27 ans auparavant. Cette "sensitivity" conjecture a été attaquée en vain par de nombreux chercheurs renommés. Or, la nouvelle preuve est si simple qu’un chercheur l’a résumé en un [tweet].
- L'objectif est de comprendre quels sont les paramètres classiques des fonctions Booléennes et des liens entre eux avant de s'intéresser à la preuve de la conjecture. On pourra essayer de construire des fonctions extrémales (ie, avec des paramètres extrémaux dans leur plage de valeurs).
- Bibliographie initiale :
- Le papier original où la question a été posée : N. Nisan, M. Szegedy. [On the degree of Boolean functions as real polynomials.] Comput. Complexity, 4 (1992), 462–467.
- Une référence sur l'analyse des fonctions Booléennes : Ryan O’Donnell. [Analysis of Boolean Functions], Cambridge University Press, 2014
- La preuve de la conjecture : Hao Huang. [Induced subgraphs of hypercubes and a proof of the Sensitivity Conjecture]. Annals of Mathematics, 190 (2019), 949-955
Structures de données purement fonctionnelles
- Tuteur : Tom Hirschowitz
- Résumé : L'algorithmique est souvent enseignée sur des langages principalement impératifs tels que C. Les structures de données utilisées ne sont pas toujours évidentes à traduire vers les langages fonctionnels tels que OCaml. L'étudiant s'initiera aux structures de données fonctionnelles et aux concepts liés tels que la persistence, en suivant le livre « Purely functional data structures » d'Okasaki.
- Liens
Automates cellulaires et décidabilité
- Tuteur : François Boussion
- Résumé : Un automate cellulaire est un modèle de calcul discret, utilisé en dans différentes sciences (informatique, mathématiques, physique, biologie, etc;). Le jeu de la vie est l'exemple emblématique d'automate cellulaire. Les règles de calcul d'un automate cellulaire, et de son évolution au cours du temps sont assez simples, mais mènent cependant à des problèmes complexes dont certains indécidables. Par exemple, déterminer si, étant donné des règles, on arrivera forcément, en un nombre fini d'étapes, dans une configuration donné, quelque soit la configuration initiale (problème de nilopotence).
- L'objectif est de s'intéresser à ces problèmes indécidables dans les automates cellulaires et de produire un mini-cours sur le sujet.
- Références
- K. JARKKO, The nilpotency problem of one-dimensional cellular automata, SIAM J. Comput., Vol. 21, No. 3, pp. 571-586, June 1992.
- K. CULIK II, J. PACHL, S. Yu, On the limit sets ofcellular automata, SIAM J. Comput., 18 (1989), pp.831-842.
travaux réalisés 2018-2019
Les exposés auront lieu le lundi 27 mai de 9h à 11h en salle 115 du chablais. Prévoyez 15-20min suivi de questions.
- Tristan Porteries (PDF): problèmes avec mémoire restreinte, tuteur S. Tavenas
- R. Wagner: Reconstruction de surfaces à partir de nuages de points, tuteur J.-O. Lachaud
- Nils Ruet (PDF): LISP, tuteur P. Hyvernat
- Rémy Bouvier (PDF): dancing links, tuteur P. Hyvernat
sujets 2018-2019
Les sujets 1-3 sont encadrés par J.-O. Lachaud, les sujets 4-5 par P. Hyvernat, le sujet 6 par S. Tavenas. Un encadrant encadre au max 2 étudiants.
- Débruitage de surfaces maillées (mesh denoising): Etant donné une surface triangulées, dont la position des sommets est "bruité" (en général par les moyens d'acquisitions utilisés pour la fabriquer), ces algorithmes tentent de retrouver la surface initiale, en supposant par exemple qu'elle était lisse ou lisse par morceaux.
- Bilateral mesh denoising, S Fleishman, I Drori, D Cohen-Or - ACM transactions on graphics (TOG), 2003 - dl.acm.org
- Mesh denoising via L0 minimization, L He, S Schaefer - ACM Transactions on Graphics (TOG), 2013 - dl.acm.org
- Variational mesh denoising using total variation and piecewise constant function space, H Zhang, C Wu, J Zhang, J Deng - IEEE transactions on …, 2015 - ieeexplore.ieee.org
- Approximation de formes: il s'agit de fabriquer, à partir d'une surface maillée précise, une nouvelle surface composée de beaucoup moins de sommets qui l'approche et qui conserve ses caractéristiques principales. Cela sert aussi en compression de formes.
- Progressive meshes, H Hoppe - Proceedings of the 23rd annual conference on SIGGRAPH, 1996 - dl.acm.org
- Variational shape approximation, D Cohen-Steiner, P Alliez, M Desbrun - ACM Transactions on Graphics …, 2004 - dl.acm.org
- Reconstruction de surfaces à partir de nuages de points: il s'agit de trouver comment fabriquer une surface qui approche un ensemble de points dans l'espace.
- Delaunay triangulation based surface reconstruction.F Cazals, J Giesen - Effective computational geometry for curves and …, 2006 - Springer
- State of the art in surface reconstruction from point clouds, M Berger, A Tagliasacchi, L Seversky, P Alliez… - EUROGRAPHICS star …, 2014 - hal.inria.fr
- Bayesian point cloud reconstruction, P Jenke, M Wand, M Bokeloh… - Computer Graphics …, 2006 - Wiley Online Library
- "dancing links" : l'algorithme X de Knuth est un algorithme élégant et "efficace" pour chercher une solution au problème combinatoire de la couverture exacte. Cet algorithme peut s'appliquer à des problèmes aussi divers que la résolution de sudoku ou le pavage par polyominos. Ce problème fait partie de la classe des problèmes NP-complets qui sont intrinsequement difficiles
- "Dancing links" : description de l'algorithme X de Knuth et de quelques applications Millennial Perspectives in Computer Science : Proceedings of the 1999 Oxford-Microsoft Symposium in Honour of Sir Tony Hoare, Palgrave, coll. « Cornerstones of Computing », 2000
- Le langage LISP est un des plus vieux langages de programmation encore (un peu) utilisé. (LISP: 1958, C: 1972, Python: 1989). Il s'agit d'un langage fonctionnel avec une syntaxe très simple. La programmation fonctionnelle s'est ensuite developpé dans plusieurs directions, notamment avec la notion de typage fort (Hindley-Milner) utilisé par les langages de la famille ML (SML, Caml)
- John McCarthy Recursive Functions of Symbolic Expressions and Their Computation by Machine, Part I description du langage LISP
- Robin Milner, A Theory of Type Polymorphism in Programming : description de l'algorithme de typage d'un langage fonctionnel
- Une question naturelle est de savoir quels sont les problèmes qui peuvent être résolus avec un espace mémoire restreint. Plus formellement, on notera L l'ensemble des problèmes que l'on peut résoudre en utilisant seulement un espace mémoire logarithmique. On s'intéresse à cette classe de problèmes, et plus particulièrement aux problèmes de connectivité dans un graphe.
- Sylvain Périfel Complexité algorithmique : Un livre récent qui survole une grosse partie de la complexité algorithmique. Le chapitre 4 concerne la complexité en espace.
- Omer Reingold Undirected Connectivity in Log-Space
travaux réalisés 2017-2018
Les exposés auront lieu le vendredi 25 mai 2018, à 9h. Prévoyez 15-20min suivi de questions.
- ray-tracing au path-tracing, Raphael Tournafond (PDF)
- "dancing links" et NP complétude, Ambroise Decouttere (PDF)
sujets 2017-2018
- Du ray-tracing au path-tracing: il s'agit de comprendre l'évolution des algorithmes de rendu (dits "réalistes") et de mettre en avant les principales évolutions.
- An introduction to ray tracing AS Glassner - 1989 - books.google.com
- Energy redistribution path tracing, D Cline, J Talbot, P Egbert - ACM Transactions on Graphics (TOG), 2005 - dl.acm.org
- et pour une introduction douce au ray-tracing: TP2 de http://www.lama.univ-savoie.fr/~lachaud/Cours/INFO805/Tests/html/index.html
- Débruitage de surfaces maillées (mesh denoising): Etant donné une surface triangulées, dont la position des sommets est "bruité" (en général par les moyens d'acquisitions utilisés pour la fabriquer), ces algorithmes tentent de retrouver la surface initiale, en supposant par exemple qu'elle était lisse ou lisse par morceaux.
- Bilateral mesh denoising, S Fleishman, I Drori, D Cohen-Or - ACM transactions on graphics (TOG), 2003 - dl.acm.org
- Mesh denoising via L0 minimization, L He, S Schaefer - ACM Transactions on Graphics (TOG), 2013 - dl.acm.org
- Variational mesh denoising using total variation and piecewise constant function space, H Zhang, C Wu, J Zhang, J Deng - IEEE transactions on …, 2015 - ieeexplore.ieee.org
- Approximation de formes: il s'agit de fabriquer, à partir d'une surface maillée précise, une nouvelle surface composée de beaucoup moins de sommets qui l'approche et qui conserve ses caractéristiques principales. Cela sert aussi en compression de formes.
- Progressive meshes, H Hoppe - Proceedings of the 23rd annual conference on SIGGRAPH, 1996 - dl.acm.org
- Variational shape approximation, D Cohen-Steiner, P Alliez, M Desbrun - ACM Transactions on Graphics …, 2004 - dl.acm.org
- Reconstruction de surfaces à partir de nuages de points: il s'agit de trouver comment fabriquer une surface qui approche un ensemble de points dans l'espace.
- Delaunay triangulation based surface reconstruction.F Cazals, J Giesen - Effective computational geometry for curves and …, 2006 - Springer
- State of the art in surface reconstruction from point clouds, M Berger, A Tagliasacchi, L Seversky, P Alliez… - EUROGRAPHICS star …, 2014 - hal.inria.fr
- Bayesian point cloud reconstruction, P Jenke, M Wand, M Bokeloh… - Computer Graphics …, 2006 - Wiley Online Library
- "dancing links" et NP complétude : l'algorithme X de Knuth est un algorithme élégant et "efficace" pour chercher une solution au problème combinatoire de la couverture exacte. Cet algorithme peut s'appliquer à des problèmes aussi divers que la résolution de sudoku ou le pavage par polyominos. Ce problème fait partie de la classe des problèmes NP-complets qui sont intrinsequement difficiles
- "Dancing links" : description de l'algorithme X de Knuth et de quelques applications Millennial Perspectives in Computer Science : Proceedings of the 1999 Oxford-Microsoft Symposium in Honour of Sir Tony Hoare, Palgrave, coll. « Cornerstones of Computing », 2000
- Classic Nintendo Games are (Computationally) Hard : preuve que Super Mario et d'autres jeux video classiques sont NP-complets Theoretical Computer Science, volume 586, 2015, pages 135–160.
- Le langage LISP est un des plus vieux langages de programmation encore (un peu) utilisé. (LISP: 1958, C: 1972, Python: 1989). Il s'agit d'un langage fonctionnel avec une syntaxe très simple. La programmation fonctionnelle s'est ensuite developpé dans plusieurs directions, notamment avec la notion de typage fort (Hindley-Milner) utilisé par les langages de la famille ML (SML, Caml)
- John McCarthy Recursive Functions of Symbolic Expressions and Their Computation by Machine, Part I description du langage LISP
- Robin Milner, A Theory of Type Polymorphism in Programming : description de l'algorithme de typage d'un langage fonctionnel