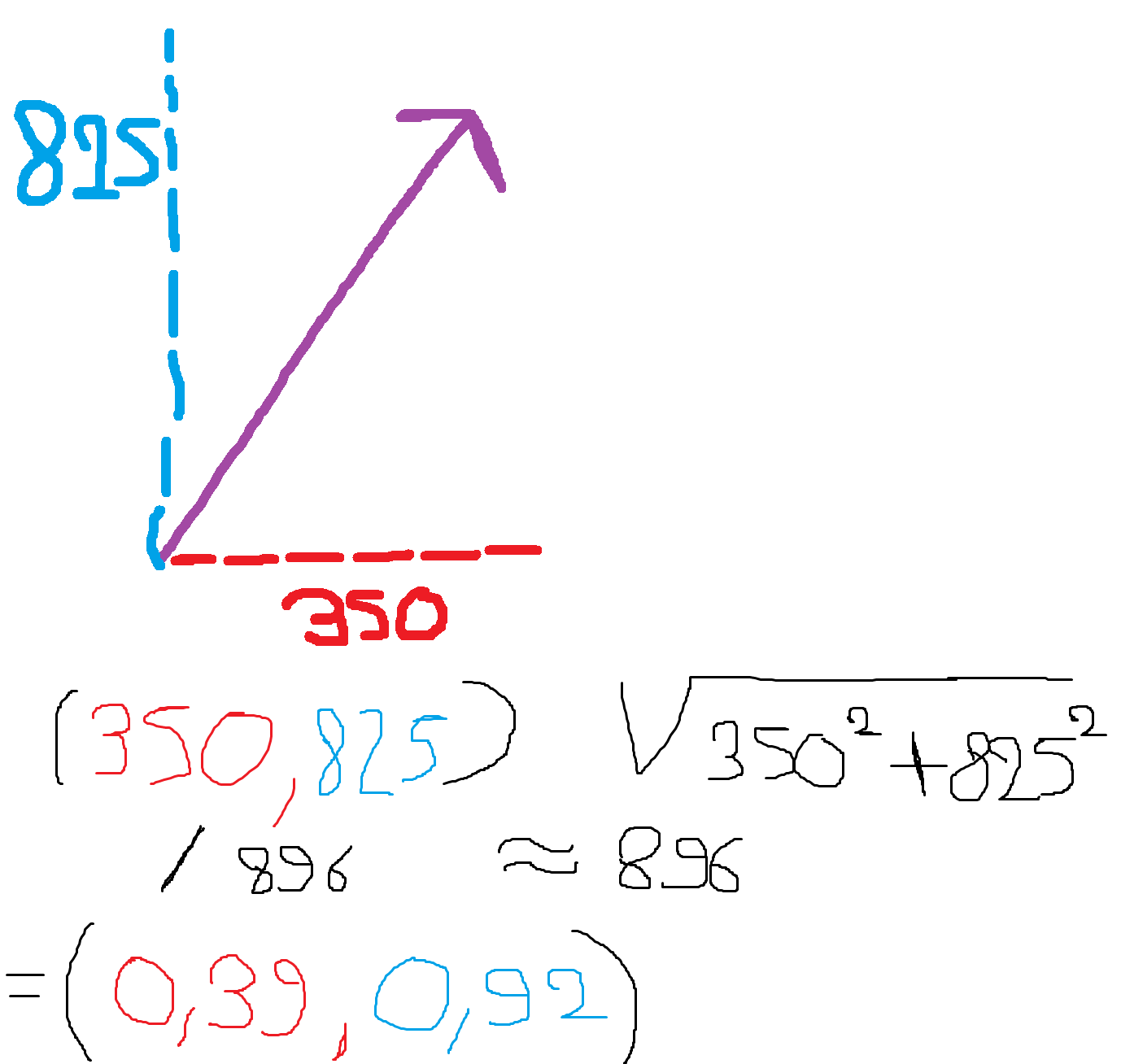« Magic Numbers et Jeux Vidéo » : différence entre les versions
Aucun résumé des modifications |
Aucun résumé des modifications |
||
| Ligne 56 : | Ligne 56 : | ||
<h1 style="font-family:Impact, Haettenschweiler, 'Arial Narrow', sans-serif">Méthode pour calculer des racines carrés</h1> |
<h1 style="font-family:Impact, Haettenschweiler, 'Arial Narrow', sans-serif">Méthode pour calculer des racines carrés</h1> |
||
Dans cette partie, nous allons donc nous intéresser à deux algorithmes : |
|||
- Celui de Newton-Raphson |
|||
- Celui de la racine carré inverse rapide |
|||
<h2 style="font-family:Impact, Haettenschweiler, 'Arial Narrow Bold', sans-serif">Méthode Newton-Raphson</h2> |
<h2 style="font-family:Impact, Haettenschweiler, 'Arial Narrow Bold', sans-serif">Méthode Newton-Raphson</h2> |
||
Version du 25 février 2025 à 00:11
Noah CUNEO
Tuteur : François BOUSSION
Introduction
Les Magic Numbers, c'est mal !
Mais nous allons voir que dans certains cas de figure... C'est plutôt ok.
Dans un premier temps, rappelons nous ce qu'est un magic number.
Nous sommes tenté de dire qu'un magic number est une constante. Et bien c'est partiellement vrai...
En réalité, une constante et une valeur nommée et explicite. Comme par exemple PI (3.1415...) ou la constante gravitationelle G (9.81).
Alors qu'un magic number est une valeur qui semble sortir de nulle part, par exemple 0x5f3759df.
Vous devez vous dire que cette valeur que j'ai donné, je la sort de nulle part. Et bien non ! Cette valeur est extrêmement utile dans bien des domaine.
D'abord faisons quelques rappels.
Normaliser un vecteur
La normalisation de vecteur est une notion importante des mathématiques et de l'informatique.
Par exemple, pour le jeu que nous avons réalisé en VISI301, nous avons dû normaliser le vecteur existante entre le centre de l'écran et la souris.
Ce dernier permettant de gérer la trajectoire d'un projectile.
Pourquoi le normaliser ? Et bien parce que si nous utilisons le vecteur dont je viens de vous parler, la balle irai plus ou moins vite en fonction de la distance entre la souris et le centre de l'écran.
Voici un rappel de comment nous pouvons normaliser un vecteur :
Nous avons maintenant un vecteur normalisé. Ainsi, notre balle aura une vitesse constante peut importe la distance de la souris.
Et nous pouvons par ailleurs multiplier notre vecteur par un scalaire pour avoir un contrôle total sur la vitesse du projectile.
On a normalisé un vecteur, c'est bien... Mais n'est ce pas un peu lent comme méthode de calcul ?
Si je vous demande de calculer la racine carré de 2531 de tête vous n'y arriverai certainement pas. Pour notre pc c'est pareil, il ne sort pas ce résultat par magie.
Pour sortir ce résultat, il utilise l'algorithme de Newton-Raphson qui permet de calculer la racine carré d'un nombre.
Intéressons nous à cet algorithme.
Méthode pour calculer des racines carrés
Dans cette partie, nous allons donc nous intéresser à deux algorithmes :
- Celui de Newton-Raphson
- Celui de la racine carré inverse rapide