« "tableau des suffixes" et transformée de Burrows-Wheeler » : différence entre les versions
(Réécriture introduction, recherche naïve, trie) |
|||
| Ligne 103 : | Ligne 103 : | ||
=== Arbre de suffixes === |
=== Arbre de suffixes === |
||
[[Fichier:Visi_201_suffix_tree_abracadabradad_imp.png|400px|thumb|right|Arbre de suffixes de "abracadabradad" avec longueurs]] |
|||
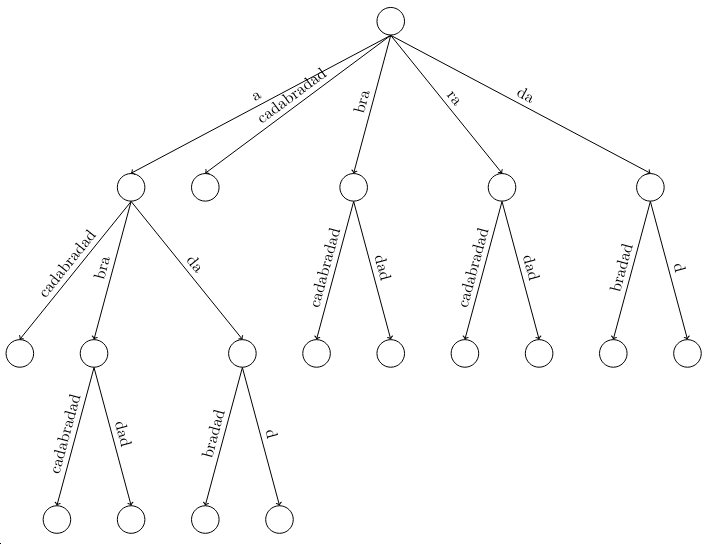
[[Fichier:Visi_201_suffix_tree_abracadabradad.png|400px|thumb|right|Arbre de suffixes de "abracadabradad" pour lecture]] |
|||
L'arbre de suffixes est un structure proche du Trie mais qui règle le problème de la taille de la structure. |
L'arbre de suffixes est un structure proche du Trie mais qui règle le problème de la taille de la structure. |
||
Pour réduire la taille du Trie, il faut réduire les chemins uniques (ceux pour lesquels les noeuds successifs n'ont qu'un unique enfant) en les rassemblant en un unique noeud (dans "panpan", on regrouperait, entre autres, "pan", "an" et "npan"). Cependant, la même quantité d'information est toujours stockée mais d'une façon différente. Pour résoudre ce problème, il faut faut considérer chaque noeud comme une information de 2 nombres sur la chaîne d'origine : l'indice de début de la sous-chaîne et la longueur ou l'indice de fin de celle-ci. L'indice de début doit toujours être supérieur à l'indice auquel se fini la sous-chaîne représenté sur la branche parente (à la racine, c'est l'indice 0) et il doit être le plus petit possible en même temps. |
|||
Pour réduire la taille du Tries, il faut considérer chaque lettre par son plus petit indice dans la chaîne de caractère en avançant à chaque fois l'indice. |
|||
Il est aussi possible de générer cette arbre d'autre manière telle que la suivante en Python qui utilise en clef l'indice du début du suffixe et sa taille : |
|||
<pre> |
|||
def convertion_tree(mot: str) -> tuple: |
|||
"""Transforme une chaîne de caractères en arbre de suffixe""" |
|||
arbre = {} |
|||
for i in range(len(mot)): |
|||
ajouter_tree(arbre, mot, i) |
|||
return (mot, arbre) |
|||
def ajouter_tree(branche: dict, mot: str, offset: int): |
|||
"""Ajouter une chaîne de caractères dans un arbre""" |
|||
keys = list(branche.keys()) |
|||
nb_total_keys = len(keys) |
|||
nb_key = 0 |
|||
est_dedans = mot[offset:] == "" |
|||
longueur_mot_a_placer = len(mot) - offset |
|||
while nb_key < nb_total_keys and not est_dedans: |
|||
key = keys[nb_key] |
|||
if mot[key[0]] == mot[offset]: |
|||
nb_egaux = 1 |
|||
stop = False |
|||
while nb_egaux < min(key[1], longueur_mot_a_placer) and not stop: |
|||
if mot[key[0] + nb_egaux] != mot[offset + nb_egaux]: |
|||
stop = True |
|||
else: |
|||
nb_egaux += 1 |
|||
if nb_egaux != longueur_mot_a_placer: |
|||
if nb_egaux == key[1]: |
|||
ajouter_tree(branche[key], mot, offset + nb_egaux) |
|||
else: |
|||
branche[(key[0], nb_egaux)] = { |
|||
(key[0] + nb_egaux, key[1] - nb_egaux): branche[key], |
|||
(offset + nb_egaux, longueur_mot_a_placer - nb_egaux): {} |
|||
} |
|||
branche.pop(key) |
|||
est_dedans = True |
|||
nb_key += 1 |
|||
if not est_dedans: |
|||
branche[(offset, len(mot) - offset)] = {} |
|||
</pre> |
|||
L'arbre de suffixes, tout comme le Trie, créé des chemins uniques pour chaque suffixe de la chaîne d'origine. En utilisant ce principe, il est possible d'effectuer une recherche dans la structure en suivant les règles suivantes : |
|||
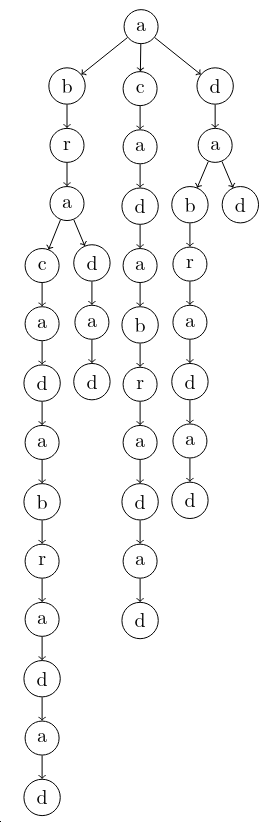
Donc en reprenant le Trie de "abracadabradad" et en transformant chaque lettre par son plus petit indice dans la chaîne ainsi que le nombre de lettre parcourue à cet endroit (soit toujours 1 actuellement), on obtient l'arbre suivant : |
|||
* S'il existe une branche dont la lettre à l'indice du début du suffixe dans la chaîne d'origine correspond à la première lettre du patern : |
|||
TRIE MAIS AVEC INDICES ET LONGUEURS |
|||
** Si le patern est inclus dans la sous-chaîne, le patern est dans la chaîne d'origine |
|||
** Si la sous chaîne est incluse dans le patern, cherche la suite du patern dans le sous-arbre correspondant à la branche |
|||
** Sinon, le patern n'est pas dans la chaîne d'origine |
|||
* Sinon, le patern n'est pas dans la chaîne d'origine |
|||
Ce qui nous donne le code Python suivant : |
|||
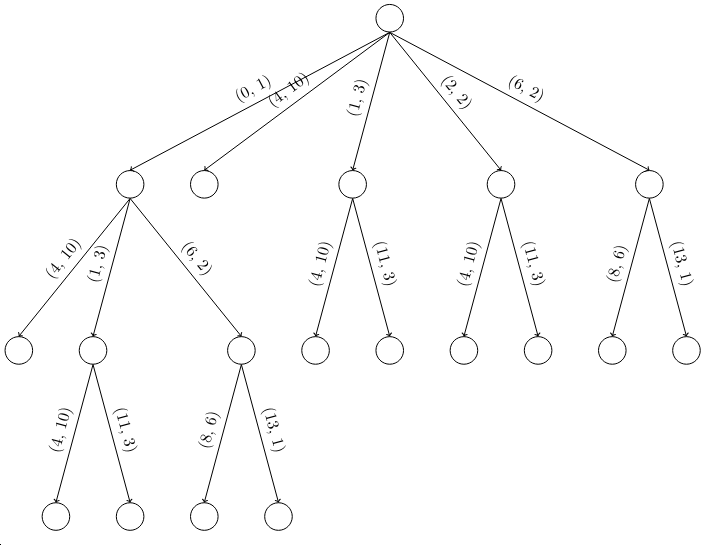
Ensuite, on vérifie pour chaque branche le nombre de sous-branches. S'il n'y a pas de sous-branche, on ne fait rien car c'est une feuille. Si une branche n'a qu'une sous branche, on les combine en précisant d'où l'on part (indice de la branche) et le nombre de lettres contenues dans cette nouvelle branche ou l'indice de fin de cette nouvelle branche. L'utilisation de l'indice de fin de la branche ou du nombre de lettres dans la branche est un choix qui doit être le même dans toutes les branches de l'arbre. |
|||
<pre> |
|||
def est_dans_tree(arbre: tuple, mot: str) -> bool: |
|||
"""Renvoie si la chaîne de caractères est contenue dans l'arbre""" |
|||
return est_dans_branche(arbre[1], arbre[0], mot) |
|||
def est_dans_branche(branche: dict, mot_origine: str, mot: str) -> bool: |
|||
En suivant de principe, on obtient l'arbre suivant pour la chaîne "abracadabradad" : |
|||
"""Renvoie si la chaîne de caractères est contenue dans la branche""" |
|||
TREE |
|||
est_dedans = mot == "" |
|||
fin = False |
|||
keys = list(branche.keys()) |
|||
nb_key = 0 |
|||
longueur_mot = len(mot) |
|||
while nb_key < len(keys) and not fin and not est_dedans: |
|||
key = keys[nb_key] |
|||
if mot_origine[key[0]] == mot[0]: |
|||
if key[1] == longueur_mot: |
|||
est_dedans = mot_origine[key[0] : key[0] + key[1]] == mot |
|||
elif longueur_mot < key[1]: |
|||
est_dedans = mot_origine[key[0] : key[0] + longueur_mot] == mot |
|||
else: |
|||
est_dedans = est_dans_branche(branche[key], mot_origine, mot[key[1]:]) |
|||
fin = True |
|||
nb_key += 1 |
|||
return est_dedans |
|||
</pre> |
|||
L'arbre de suffixes présente plusieurs avantages : |
|||
On peut constater que l'arbre est plus petit que le Trie, mais que cependant il est plus compliqué à comprendre. De plus, pour le construire, on utilise le Trie ce qui implique que la construction de la structure est d'une complexité au moins quadratique, ce qui ne règle pas le problème de la construction longue lorsque les chaînes de caractère sont grandes. Il est cependant possible de régler ce problème en construisant l'arbre grâce à l'[https://fr.wikipedia.org/wiki/Algorithme_d%27Ukkonen algorithme de Ukkonen], qui permet de construire l'arbre de suffixes avec une complexité linéaire. |
|||
* Il a une taille réduite (<math>O(n)</math> avec <math>n</math> la taille de la chaîne d'origine |
|||
* Simple à comprendre |
|||
* Recherche rapide (<math>O(m)</math> avec <math>m</math> la taille du patern) |
|||
* Peut être construit grâce au Trie |
|||
Mais celui-ci présente aussi des désavantages : |
|||
* Plus complexe à implémenter |
|||
* Sa taille reste grande : la structure est lourde, surtout pour de grandes chaînes de caractères |
|||
Il est aussi possible de construire l'arbre de suffixes de manière plus efficace (construction en <math>O(n)</math> au lieu de <math>O(n^2)</math> avec <math>n</math> la taille de la chaîne de caractères d'origine) en utilisant par exemple l'[https://fr.wikipedia.org/wiki/Algorithme_d%27Ukkonen algorithme de Ukkonen]. |
|||
Afin de rechercher dans l'arbre de suffixes la présence d'un paterne, il suffit de suivre le même algorithme que celui du Trie en remplaçant chaque indice par sa lettre à la position de l'indice dans le mot ainsi que de prendre en compte que la branche n'est pas forcément de longueur 1, mais peut être plus longue. |
|||
=== Tableau de suffixes === |
=== Tableau de suffixes === |
||
Version du 15 mai 2025 à 12:29
Étudiant : BOGDAN Benjamin
Tuteur : TAVENAS Sébastien
Introduction
La recherche de patern dans une chaîne de caractères est un problème récurrent qui peut rapidement poser problème lorsque l'on cherche plusieurs fois dans une chaîne de caractères de grande taille.
Un patern est aussi une chaîne de caractères.
Recherche dans une chaîne de caractères
Recherche naïve
L'algorithme naïf pour rechercher une chaîne de caractères dans une autre consiste à regarder dans l'ordre la chaîne de caractères dans laquelle on cherche la sous-chaîne et de vérifier si les caractères correspondent ou non.
Nous pouvons l'implémenter comme suivant en Python :
def est_dans(sous_chaine: str, chaine: str) -> bool:
"""Renvoie si la sous chaîne est dans la chaîne"""
dedans = False
i = 0
while i < len(chaine) and not dedans:
offset = 0
stop = False
while i + offset < len(chaine) and offset < len(sous_chaine) and not stop:
if sous_chaine[offset] != chaine[i+offset]:
stop = True
offset += 1
if not stop:
dedans = True
i += 1
return dedans
L'avantage de cet algorithme est qu'il est facile à comprendre et à implémenter. Cependant, bien qu'il puisse être optimisé et évitant certaines comparaisons, il est très lent à l'exécution car il est de complexité quadratique, impliquant donc qu'il n'est pas efficace sur de très grandes chaînes.
Afin de palier à ce problème, il est possible de créer des structures de données différentes qui ont pour but de représenter tous les suffixes existant d'une chaîne de caractère et qui permet de les identifier de manière unique. Ces conditions impliquent que toutes les sous-chaînes de la chaîne décomposée seront représenté à l'intérieur de la structure et seront plus facilement extrayables.
Pour effectuer la recherche du patern dans notre chaîne de caractère grâce aux différentes structures, il faut partir du principe que chaque sous-chaîne dans la chaîne d'origine est toujours préfixe d'un suffixe.
Trie (Arbre de préfixes)
Le Trie est un structure permettant de représenter tous les suffixes d'une chaîne de caractères sous la forme d'un arbre. Chaque chemin allant de la racine de l'arbre à une de ses feuilles représente un suffixe différent. Chaque branche de l'arbre est une lettre et mène soit à une feuille soit à un sous Trie qui permet la représentation de la suite du suffixe.
Il est possible de créer le Trie en ajoutant successivement chaque suffixe de la chaîne de caractère à la racine de l'arbre en respectant les règles suivantes :
- Si une branche de l'arbre correspond à la première lettre du suffixe à ajouter, il faut ajouter la suite du suffixe dans le sous-arbre de cette branche
- Sinon créer une branche correspondant à la première lettre du suffixe à ajouter et ajouter la suite du suffixe dans le sous-arbre de cette nouvelle branche
Cela nous donne le code python suivant :
def tries(mot: str) -> dict:
"""Transforme une chaîne de caractère en tries"""
res = {}
for i in range(len(mot)):
actuel = res
for n in range(i, len(mot)):
actuel[mot[n]] = actuel.get(mot[n], {})
actuel = actuel[mot[n]]
return res
La recherche dans le Trie consiste à regarder s'il existe un chemin pour lequel chaque valeur des branches dans l'ordre correspond à chaque lettre du patern recherché.
On suit donc les règles suivantes:
- Si une branche du Trie correspond à la première lettre du patern, chercher le patern dans le sous-Trie correspondant de la branche
- Sinon, le patern n'est pas dans la chaîne
Cet algorithme donne le code Python suivant :
def est_dans_tries(tries: dict, mot: str) -> bool:
"""Renvoie si une chaîne de caractère est décomposée dans le tries"""
res = True
i = 0
actuel = tries
while i < len(mot) and res:
prochain = actuel.get(mot[i], None)
if prochain != None:
actuel = prochain
else:
res = False
i += 1
return res
Cette structure présente plusieurs avantages :
- Facile à comprendre (construction et recherche)
- Facile à implémenter
- Recherche en (: la longueur de la chaîne recherchée)
Cependant elle présente aussi plusieurs désavantages :
- Construction en O(n^2) (n: la longueur de la chaîne qui génère l'arbre)
- Complexité spatiale en O(n^2) (n: la longueur de la chaîne qui génère l'arbre)
Arbre de suffixes
L'arbre de suffixes est un structure proche du Trie mais qui règle le problème de la taille de la structure.
Pour réduire la taille du Trie, il faut réduire les chemins uniques (ceux pour lesquels les noeuds successifs n'ont qu'un unique enfant) en les rassemblant en un unique noeud (dans "panpan", on regrouperait, entre autres, "pan", "an" et "npan"). Cependant, la même quantité d'information est toujours stockée mais d'une façon différente. Pour résoudre ce problème, il faut faut considérer chaque noeud comme une information de 2 nombres sur la chaîne d'origine : l'indice de début de la sous-chaîne et la longueur ou l'indice de fin de celle-ci. L'indice de début doit toujours être supérieur à l'indice auquel se fini la sous-chaîne représenté sur la branche parente (à la racine, c'est l'indice 0) et il doit être le plus petit possible en même temps.
Il est aussi possible de générer cette arbre d'autre manière telle que la suivante en Python qui utilise en clef l'indice du début du suffixe et sa taille :
def convertion_tree(mot: str) -> tuple:
"""Transforme une chaîne de caractères en arbre de suffixe"""
arbre = {}
for i in range(len(mot)):
ajouter_tree(arbre, mot, i)
return (mot, arbre)
def ajouter_tree(branche: dict, mot: str, offset: int):
"""Ajouter une chaîne de caractères dans un arbre"""
keys = list(branche.keys())
nb_total_keys = len(keys)
nb_key = 0
est_dedans = mot[offset:] == ""
longueur_mot_a_placer = len(mot) - offset
while nb_key < nb_total_keys and not est_dedans:
key = keys[nb_key]
if mot[key[0]] == mot[offset]:
nb_egaux = 1
stop = False
while nb_egaux < min(key[1], longueur_mot_a_placer) and not stop:
if mot[key[0] + nb_egaux] != mot[offset + nb_egaux]:
stop = True
else:
nb_egaux += 1
if nb_egaux != longueur_mot_a_placer:
if nb_egaux == key[1]:
ajouter_tree(branche[key], mot, offset + nb_egaux)
else:
branche[(key[0], nb_egaux)] = {
(key[0] + nb_egaux, key[1] - nb_egaux): branche[key],
(offset + nb_egaux, longueur_mot_a_placer - nb_egaux): {}
}
branche.pop(key)
est_dedans = True
nb_key += 1
if not est_dedans:
branche[(offset, len(mot) - offset)] = {}
L'arbre de suffixes, tout comme le Trie, créé des chemins uniques pour chaque suffixe de la chaîne d'origine. En utilisant ce principe, il est possible d'effectuer une recherche dans la structure en suivant les règles suivantes :
- S'il existe une branche dont la lettre à l'indice du début du suffixe dans la chaîne d'origine correspond à la première lettre du patern :
- Si le patern est inclus dans la sous-chaîne, le patern est dans la chaîne d'origine
- Si la sous chaîne est incluse dans le patern, cherche la suite du patern dans le sous-arbre correspondant à la branche
- Sinon, le patern n'est pas dans la chaîne d'origine
- Sinon, le patern n'est pas dans la chaîne d'origine
Ce qui nous donne le code Python suivant :
def est_dans_tree(arbre: tuple, mot: str) -> bool:
"""Renvoie si la chaîne de caractères est contenue dans l'arbre"""
return est_dans_branche(arbre[1], arbre[0], mot)
def est_dans_branche(branche: dict, mot_origine: str, mot: str) -> bool:
"""Renvoie si la chaîne de caractères est contenue dans la branche"""
est_dedans = mot == ""
fin = False
keys = list(branche.keys())
nb_key = 0
longueur_mot = len(mot)
while nb_key < len(keys) and not fin and not est_dedans:
key = keys[nb_key]
if mot_origine[key[0]] == mot[0]:
if key[1] == longueur_mot:
est_dedans = mot_origine[key[0] : key[0] + key[1]] == mot
elif longueur_mot < key[1]:
est_dedans = mot_origine[key[0] : key[0] + longueur_mot] == mot
else:
est_dedans = est_dans_branche(branche[key], mot_origine, mot[key[1]:])
fin = True
nb_key += 1
return est_dedans
L'arbre de suffixes présente plusieurs avantages :
- Il a une taille réduite ( avec la taille de la chaîne d'origine
- Simple à comprendre
- Recherche rapide ( avec la taille du patern)
- Peut être construit grâce au Trie
Mais celui-ci présente aussi des désavantages :
- Plus complexe à implémenter
- Sa taille reste grande : la structure est lourde, surtout pour de grandes chaînes de caractères
Il est aussi possible de construire l'arbre de suffixes de manière plus efficace (construction en au lieu de avec la taille de la chaîne de caractères d'origine) en utilisant par exemple l'algorithme de Ukkonen.
Tableau de suffixes
La tableau de suffixes est une structure prenant encore moins de place que l'arbre de suffixes et qui permet aussi une recherche plus rapide que celui-ci.
Le principe du tableau de suffixes est de stocker chaque suffixe d'une chaîne de caractère par l'indice de début du suffixe dans l'ordre alphabétique du suffixe (donc "abra" viendra avant "ada" car "b" vient avant "d"). Ainsi, une chaîne de n caractères produira un tableau de suffixes à n éléments.
Ainsi, pour un chaîne de caractère c de taille n, on génère le tableau T=[0, 1, 2, ..., n-1] et on trie chaque élément de T en mettant T[a] avant T[b] si et seulement si c[T[a]:] < c[T[b]:], sinon T[b] viendra avant T[a].
L'algorithme de trie choisit définira la complexité temporel de construction de la structure.
La recherche dans le tableau de suffixes est plus efficace que dans une autre des structures présentées car nous avons un tableau totalement trié, ce qui nous permet d'utiliser la dichotomie afin de rechercher un paterne dans la chaîne de caractère (complexité de O(nlog(n))).
Voici, ci-dessous, l'algorithme de la recherche dans le tableau de suffixes
def est_dans_suffix_array(suffix_array: tuple, mot: str) -> bool:
res = False
mot_origine = suffix_array[0]
array = suffix_array[1]
longueur_mot_origine = len(mot_origine)
longueur_mot = len(mot)
debut = 0
fin = len(array) - 1
while debut <= fin and not res:
mil = (debut + fin) // 2
val_mil = array[mil]
sous_mot = mot_origine[val_mil: min(val_mil + longueur_mot, longueur_mot_origine)]
if mot == sous_mot:
res = True
elif mot < sous_mot:
fin = mil - 1
else:
debut = mil + 1
return res