« Modèle proie-prédateur sans équations » : différence entre les versions
| Ligne 619 : | Ligne 619 : | ||
== Conclusion == |
== Conclusion == |
||
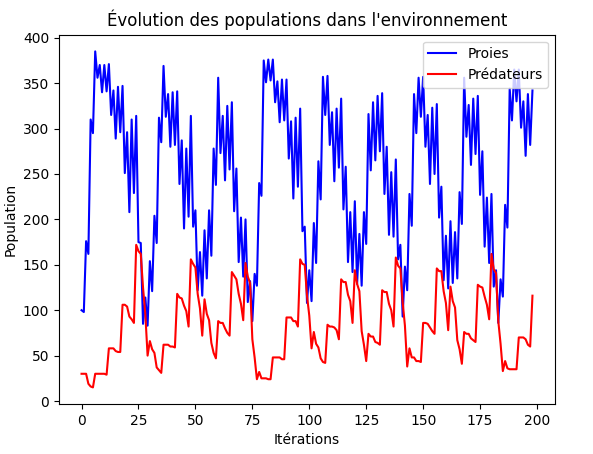
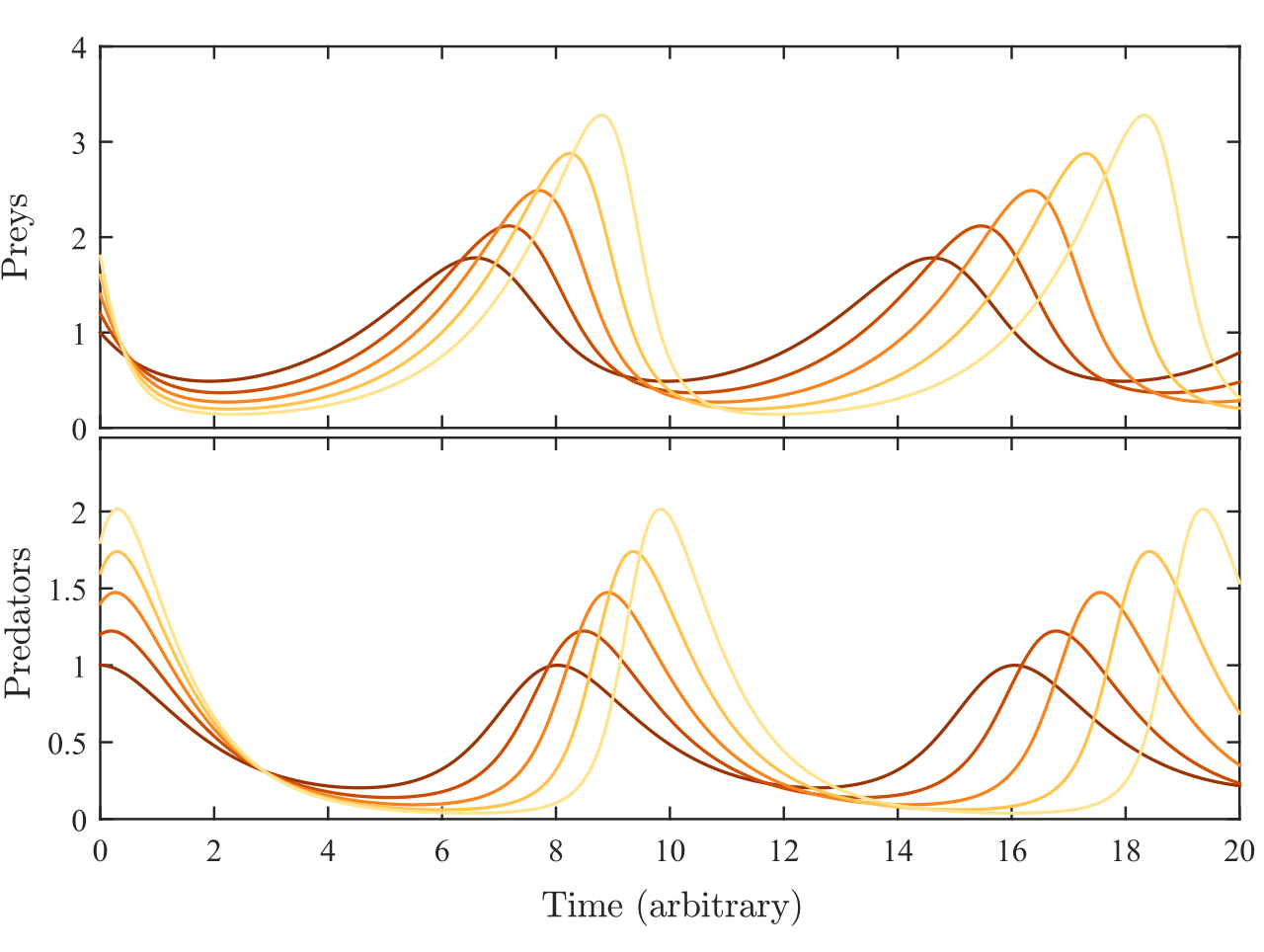
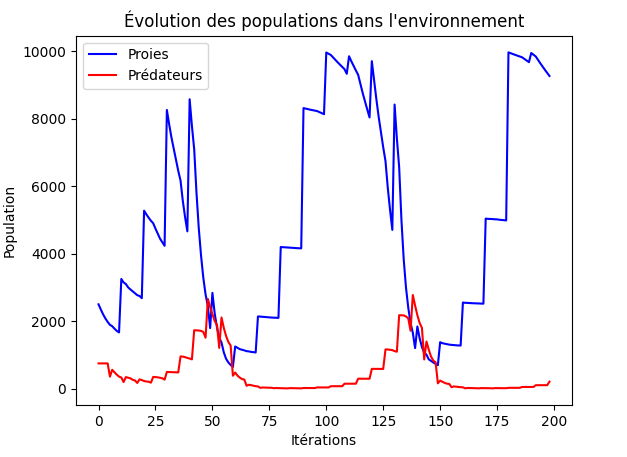
On remarque donc que nous avons bien réussit à obtenir les mêmes résultats qu'avec les équations de Lotka-Volterra |
On remarque donc que nous avons bien réussit à obtenir les mêmes résultats qu'avec les équations de Lotka-Volterra |
||
[[Fichier:Stat 1.png]] |
|||
[[Fichier:Equation.png]] |
|||
Version du 18 mai 2025 à 12:42
Etudiant : Delamézière Lucas
Tuteur : Mouloud Kessar
Introduction au problème
Les équations de Lotka-Volterra permettent d’étudier et de prédire mathématiquement l’évolution des populations de proies et de prédateurs au sein d’un même environnement.
Mais est-il possible d’obtenir les mêmes résultats avec des déplacements aléatoires sur une grille ? C’est ce que nous allons examiner aujourd'hui.
règles
Afin de créer une simulation correctement, il va falloir dans un premier temps mettre en place des "règles" qui régirons notre environnement.
règles de base
Les règles les plus importantes (celles qui sont imposées) sont les suivantes :
- nr_pred, nr_proie deux variables traduisant le nombre d'itération que prennent chaque espèces à se reproduire
- n_faim traduisant le nombre d'itération que prend un prédateur à mourir sans manger de prédateur
- La marche aléatoire, un concept très simple et portant très important pour notre simulation : chaque entité se déplacera aléatoirement (si possible) dans une de ces quatre directions (haut, bas, gauche, droite)
- Une proie est mangée lorsqu'elle se trouve au même endroit qu'un prédateur
autres règles
Il existe également d'autres règles moins évidentes, qu'il est important de définir avant l'implémentation afin de gagner du temps sur ces problématiques qui peuvent se poser lors de l'implémentation :
- Que faire si une entité essaie de sortir de l'environnement ?
- Que faire si deux entités de la même espèce vont au même endroit ?
- Priorité de reproduction, de déplacement ?
Réponses :
- rebond sur les bords.
- pas de superposition.
- les prédateurs auront la priorité.
(Ces règles sont établies temporairement et peuvent être modifiées si besoin lors de l'implémentation, à la différence des règles de base)
Pseudo code
Avant de se lancer directement dans l'implémentation, il est intelligent d'utiliser les règles que nous avons définit ci-dessus afin de réaliser un pseudo code, qui nous permettra de gagner du temps lors de l'implémentation.
##### Phase d'initialisation #####
Créer une liste `tab_proie` vide
Créer une liste `tab_predateur` vide
POUR i allant de 1 à `nb_proies_initiale` FAIRE :
Trouver une coordonnée vide dans `environnement`
SI une coordonnée est trouvée :
Ajouter une nouvelle Proie à `tab_proie`
FIN POUR
POUR j allant de 1 à `nb_predateurs_initiale` FAIRE :
Trouver une coordonnée vide dans `environnement`
SI une coordonnée est trouvée :
Ajouter un nouveau Prédateur à `tab_predateur`
FIN POUR
##### début de la simulation #####
POUR chaque tour de simulation de 1 à `nb_itérations` FAIRE :
Réinitialiser la grille `environnement` (remplir de 0)
##### Phase d'action #####
POUR chaque prédateur DANS `tab_predateur` (copie pour sécurité) :
Déplacer le prédateur en fonction de l’environnement et des proies
Vérifier s’il mange une proie, sinon décrémenter sa faim
SI faim == 0 :
Supprimer le prédateur de `tab_predateur`
SI le prédateur est toujours vivant :
Afficher ses informations
Afficher le prédateur sur la grille
FIN POUR
POUR chaque proie DANS `tab_proie` :
Déplacer la proie en fonction de l’environnement et des prédateurs
Afficher la proie sur la grille
FIN POUR
##### Phase de reproduction #####
SI c’est un tour de reproduction des prédateurs :
POUR chaque prédateur existant :
Trouver une coordonnée vide dans `environnement`
SI une coordonnée est trouvée :
Ajouter un nouveau Prédateur à `tab_predateur`
Afficher tous les prédateurs mis à jour
Afficher un message "Reproduction des prédateurs !"
SI c’est un tour de reproduction des proies :
POUR chaque proie existante :
Trouver une coordonnée vide dans `environnement`
SI une coordonnée est trouvée :
Ajouter une nouvelle Proie à `tab_proie`
Afficher toutes les proies mises à jour
Afficher un message "Reproduction des proies !"
##### Fin de la phase de reproduction #####
Afficher l’environnement mis à jour
FIN POUR
Implémentation
Le code en lui-même
Pour ce projet, l'implémentation sera réalisé en python à l'aide de programmation orienté objet
Le programme sera divisé en quatre parties qui sont les suivantes :
Le programme principal
C'est ici qu'est réalisé la simulation en elle même en utilisant les autres éléments réalisés ci-dessous.
def execution_environnement(largeur:int,longueur:int,nb_itérations:int,nb_predateurs_initiale:int,faim_predateur_initale:int,nb_proies_initiale:int,nrpred:int,nrproie:int):
environnement = [[0 for j in range(largeur)] for i in range(longueur)]
csv_columns=["population_predateurs","population_proies"]
######################################################################################
#Programme principal
#Creation des entités
tab_proie = []
tab_predateur = []
for i in range(nb_proies_initiale):
coord = trouve_coordonnees_vide(environnement, tab_proie, tab_predateur)
if coord != None:
tab_proie.append(Proie(coord[0], coord[1], nrproie))
for j in range(nb_predateurs_initiale):
coord = trouve_coordonnees_vide(environnement, tab_proie, tab_predateur)
if coord != None:
tab_predateur.append(Predateur(coord[0], coord[1], faim_predateur_initale, nrpred))
############################
with open(csv_file, mode="w", newline="") as file:
writer = csv.writer(file, delimiter=";")
writer.writerow(csv_columns)
for i in range(1,nb_itérations):
writer.writerow([len(tab_predateur), len(tab_proie)])
environnement = [[0 for _ in range(largeur)] for _ in range(longueur)]
for proie in tab_proie:
proie.se_deplacer(environnement,tab_proie,tab_predateur)
proie.afficher(environnement)
nouveau_tab_predateurs = []
for predateur in tab_predateur:
predateur.se_deplacer(environnement, tab_proie, tab_predateur)
if predateur.décompte_faim > 0:
nouveau_tab_predateurs.append(predateur) # Garde le prédateur en vie
predateur.afficher(environnement)
tab_predateur = nouveau_tab_predateurs
###### reproduction ########
if est_iteration_apparition(i,nrproie):
for _ in range(len(tab_proie)):
coord = trouve_coordonnees_vide(environnement, tab_proie, tab_predateur)
if coord != None:
tab_proie.append(Proie(coord[0], coord[1], nrproie))
for proie in tab_proie:
proie.afficher(environnement) # On affiche les nouvelles proies sur la grille
print("reproduction proies !",i)
if est_iteration_apparition(i,nrpred):
for i in range(len(tab_predateur)):
coord=(randint(0,largeur-1),randint(0,longueur-1))
tab_predateur.append(Predateur(coord[0], coord[1], faim_predateur_initale, nrpred))
for proie in tab_proie:
if proie.x == tab_predateur[i].x and proie.y == tab_predateur[i].y:
tab_proie.remove(proie)
for predateur in tab_predateur:
predateur.afficher(environnement) # On affiche les nouveaux prédateurs sur la grille
print("reproduction predateurs !",i)
###### fin reproduction ########
afficher_environnement(environnement)
print("les proies sont au nombre de:",len(tab_proie),"à la fin de la simulation")
print("les predateurs sont au nombre de:",len(tab_predateur),"à la fin de la simulation")
Vous remarquerez que certaine ligne ne sont pas les mêmes que dans le pseudo code ou même que certaines règles n'ont pas été respectées, tout cela est normal car vous verrez par la suite que nous avons été forcés de faire des changement pour le bon fonctionnement de la simulation et pour son optimisation.
La class Prédateur
Cette classe comme son nom l'indique sert à créer une entité de type prédateur, elle contient les attributs (définis dans le init) et méthodes (fonctions de la class) nécessaires à son bon fonctionnement
class Predateur:
def __init__(self, x: int, y: int, n_faim: int, nrpred:int):
self.x = x
self.y = y
self.nrpred=nrpred
self.reproduction = 0
self.n_faim = n_faim
self.décompte_faim = n_faim
def afficher(self,environnement):
'''Affiche le prédateur sur la grille'''
environnement[self.y][self.x] = 2
def se_deplacer(self, environnement: list, tab_proie: list, tab_predateur:list):
'''Déplacement du prédateur'''
tab_direction=[(0,1),(1,0),(0,-1),(-1,0)]
shuffle(tab_direction)
direction = tab_direction[0]
i=1
while (not verification_direction_possible_bordures(self, direction, environnement) or not self.verification_direction_possible_autre_predateur(direction,tab_predateur)) and i<=3:
direction=tab_direction[i]
i+=1
if i==4:
direction=(0,0)#Pas de déplacement si aucune direction trouvée
self.verification_mange_proie(environnement,direction, tab_proie)
#Déplacement du prédateur
self.x += direction[0]
self.y += direction[1]
def verification_direction_possible_autre_predateur(self, direction:tuple, tab_predateur: list):
'''Vérifie si le prédateur ne se dirige pas vers un autre predateur'''
for predateur in tab_predateur:
if predateur.x == self.x+direction[0] and predateur.y == self.y+direction[1]:
return False
return True
def verification_mange_proie(self,environnement,direction:tuple, tab_proie: list):
'''vérifie si le prédateur mange une proie'''
new_x=self.x+direction[0]
new_y=self.y+direction[1]
for proie in tab_proie[:]: # Copie pour éviter modification en boucle
if proie.x == new_x and proie.y == new_y:
tab_proie.remove(proie) # La proie est mangée
self.décompte_faim = self.n_faim
environnement[proie.y][proie.x]=0
# Réduction de la faim si rien n'a été mangé
self.décompte_faim -= 1
La class Proie
class Proie:
def __init__(self, x: int, y: int, nrproie: int):
self.x = x
self.y = y
self.nrproie = nrproie
self.reproduction = 0
def afficher(self,environnement):
'''Affiche la proie sur la grille'''
environnement[self.y][self.x] = 1
def se_deplacer(self,environnement: list,tab_proie,tab_predateur):
'''Fonction qui permet de déplacer une proie aléatoirement'''
tab_direction=[(0,1),(1,0),(0,-1),(-1,0)]
shuffle(tab_direction)
direction = tab_direction[0]
i=1
while (not verification_direction_possible_bordures(self, direction, environnement) or not self.verification_direction_possible_autre_proie(direction, tab_proie) or not self.verification_direction_possible_predateur(direction,tab_predateur)) and i<=3 :
direction=tab_direction[i]
i+=1
if i==4:
direction=(0,0)#Pas de déplacement si aucune direction trouvée
#Déplacement de la proie
self.x += direction[0]
self.y += direction[1]
def verification_direction_possible_autre_proie(self, direction:tuple, tab_proie: list):
'''Vérifie si la proie ne se dirige pas vers une autre proie'''
for proie in tab_proie:
if proie.x == self.x+direction[0] and proie.y == self.y+direction[1]:
return False
return True
def verification_direction_possible_predateur(self, direction:tuple, tab_pred: list):
'''Vérifie si la proie ne se dirige pas vers un predateur'''
for pred in tab_pred:
if pred.x == self.x+direction[0] and pred.y == self.y+direction[1]:
return False
return True
Les fonctions utilitaires
Les fonctions que j'ai appelées "utilitaires" sont des fonctions soit utilisées dans le programme principale, soit des fonctions communes aux deux classes que je n'ai pas voulu dupliquer ou soit des fonctions utiles pour le débogage.
def verification_direction_possible_bordures(self, direction: int, environnement: list):
'''Vérifie si le déplacement est faisable par rapport aux bordures'''
new_x=self.x+direction[0]
new_y=self.y+direction[1]
if new_y >= len(environnement) or new_y < 0 or new_x >= len(environnement[0]) or new_x < 0:
return False
return True
def afficher_environnement(environnement: list):
'''Affichage de la grille'''
print()
for ligne in environnement:
print(ligne)
print()
def trouve_coordonnees_vide(environnement: list, tab_proie: list, tab_predateur: list):
'''Trouve une case qui est vide (elle n'est occupée ni par une proie ni par un prédateur)'''
cases_vides = []
for y in range(len(environnement)):
for x in range(len(environnement[0])):
est_occupe = False
for proie in tab_proie:
if proie.x == x and proie.y == y:
est_occupe = True
for predateur in tab_predateur:
if predateur.x == x and predateur.y == y:
est_occupe = True
if not est_occupe:
cases_vides.append((x, y))
if len(cases_vides) > 0:
index = randint(0, len(cases_vides) - 1)
return cases_vides[index]
return None # Retourne None si aucune case vide n'est trouvée
def info_predateur(predateur: Predateur):
'''Affiche les informations d'un predateur'''
print(f'Prédateur: x={predateur.x}, y={predateur.y}, décompte_faim={predateur.décompte_faim}')
def info_proie(proie: Proie):
'''Affiche les informations d'une proie'''
print(f'Proie: x={proie.x}, y={proie.y}')
def est_iteration_apparition(i,nr_entite):
"""Verifie si l'iteration actuelle i est une itération ou une entite se reproduit """
return i % nr_entite == 0
Vérification de l'implémentation
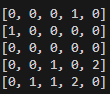
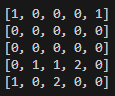
Voici 3 itérations d'une simulation sur une grille 5x5 avec 5 proies et 2 prédateurs (proie = 1, prédateur = 2, case vide = 0)
On remarque bien que tout fonctionne comme prévu, sachant que n_faim était ici égal à 2, les prédateurs qui n'ont pas eu le temps de manger une proie en 2 itérations (ici tous) disparaissent
Extractions de données
Maintenant que notre simulation fonctionne à première vue, nous allons extraire nos données sous la forme de deux colonnes : | population prédateurs | population proies | stockées dans un fichier .csv (dont vous pouvez voir l'implémentation dans le programme principale).
Nous n'avons plus qu'à extraire ces données du .csv les afficher à l'aide de matplotlib de la manière suivante :
import numpy as np
import matplotlib.pyplot as plt
import csv
def extraction_donnees_csv(fichier):
population_predateurs = []
population_proies = []
with open(fichier, mode="r", encoding="utf-8") as f:
reader = csv.reader(f, delimiter=";")
next(reader)
for ligne in reader:
if len(ligne) >= 2:
population_predateurs.append(int(ligne[0]))
population_proies.append(int(ligne[1]))
return population_predateurs, population_proies
fichier_csv = "pred_30_proies_50_faim_4_nrpred_5_nrproie_3.csv"
preds, proies = extraction_donnees_csv(fichier_csv)
preds = np.array(preds)
proies = np.array(proies)
iterations = np.arange(len(proies))
print("Population prédateurs :", preds)
print()
print("Population proies :", proies)
plt.plot(iterations, proies, label="Proies", color="green")
plt.plot(iterations, preds, label="Prédateurs", color="red")
plt.xlabel("Itérations")
plt.ylabel("Population")
plt.title("Évolution des populations dans l'environnement")
plt.legend()
plt.show()
Premiers résultats
Quelques résultats avec les mêmes paramètres
Ici, les paramètres utilisés sont les suivants:
| Paramètre | Valeur |
|---|---|
| Taille | 10 x 10 |
| Itérations | 100 |
| Prédateurs initiaux | 30 |
| Proies initiales | 50 |
| n_faim | 4 |
| nr_pred | 5 |
| nr_proie | 3 |
Lorsqu'on a cité les règles de bases, l'une d'entre elles était la marche aléatoire, et bien cette règle impacte aussi les résultats. Comme vous pouvez le voir, avec les mêmes paramètres initiaux, on arrive à générer de nouveaux résultats tous différents à chaque simulation.
Erreurs rencontrées
On a également remarqué que certaines configurations posaient problème :
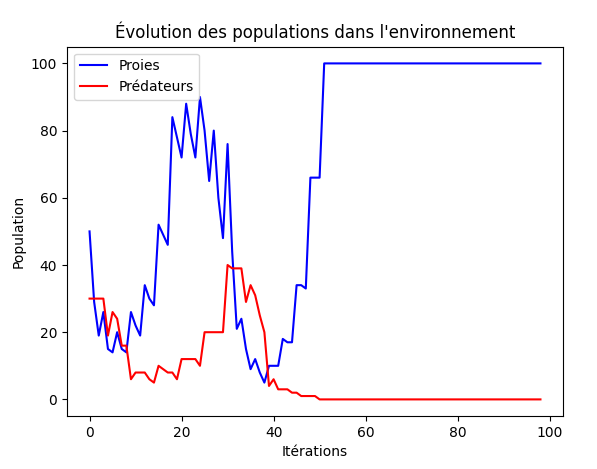
un exemple serait ce graphique qui ne fait aucun sens car les prédateurs continuent de subsister alors que les proies ont disparus.
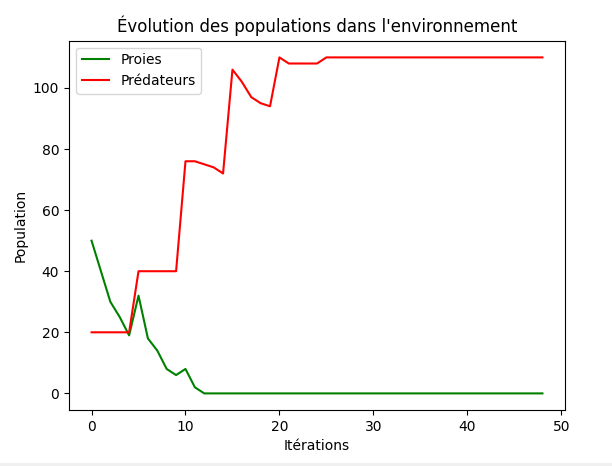
Cette erreur ce produit lorsque n faim > nr pred ce qui provoque le fait que les prédateurs se reproduisent avant de mourir de faim, ils ne disparaissent donc pas.
On peux citer également une autre erreur qui nous a forcer cette fois ci à donner la priorité d'apparition et de déplacement aux proies.
Exploration paramétrique
Dans cette partie, nous allons voir comment générer une grande quantité de simulations afin de pouvoir tester un grands nombre de paramètres.
Utilisation de bash
Pour pouvoir effectuer toutes ces simulations automatiquement, nous allons utiliser le script bash ci-dessous qui va nous permettre de stocker nos résultats sous la forme d'une arborescence de dossiers dont chaque dossiers contiendra plusieurs sous-dossiers, ces sous dossiers seront différentes valeurs testés pour un paramètre.
largeur=100;
longueur=100;
iterations=200;
job="/home/kessar/projet_VISI_LUCAS/large_simus/job.sh"
simu="/home/kessar/projet_VISI_LUCAS/large_simus/simu.py"
for i in 750
do
mkdir predateurs_$i
cd predateurs_$i
for j in 2500
do
mkdir proies_$j
cd proies_$j
for t in 3 5 10 20
do
mkdir faim_$t
cd faim_$t
for x in 4 6 10 20 30 40 50
do
mkdir nrpred_$x
cd nrpred_$x
for y in 6 10 20 30 40 50
do
mkdir nrproie_$y
cd nrproie_$y
echo "$largeur" > input.txt;
echo "$longueur" >> input.txt;
echo "$iterations" >> input.txt;
echo "$i" >> input.txt;
echo "$j" >> input.txt;
echo "$t" >> input.txt;
echo "$x" >> input.txt;
echo "$y" >> input.txt;
ln -s $simu script.py
cp $job job.sh
sbatch job.sh
cd ../
done
cd ../
done
cd ..
done
cd ../
done
cd ..
done
cd ..
Ce script va donc nous permettre de générer cette arborescence et d'exécuter également le job qui suit pour executer la simulation en elle même
#!/bin/bash #SBATCH --job-name=ProjetLuca #SBATCH --partition=weekend #SBATCH --ntasks=1 #SBATCH --cpus-per-task=1 #SBATCH --mem=4GB #SBATCH --time=24:00:00 python3 script.py
Ces job vont donc être tous êtres tous exécutés par une machine possédant 2 Intel Xeon Gold 6430 avec 32 cœurs chacun (hyperthread x2) et c'est comme ça que nous allons générer tout ces résultats.
Résultats obtenus
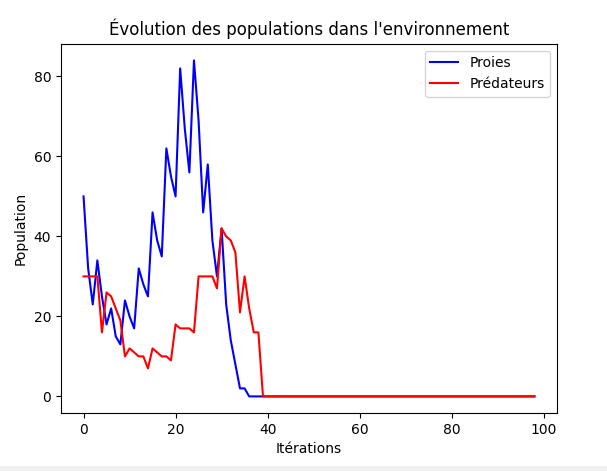
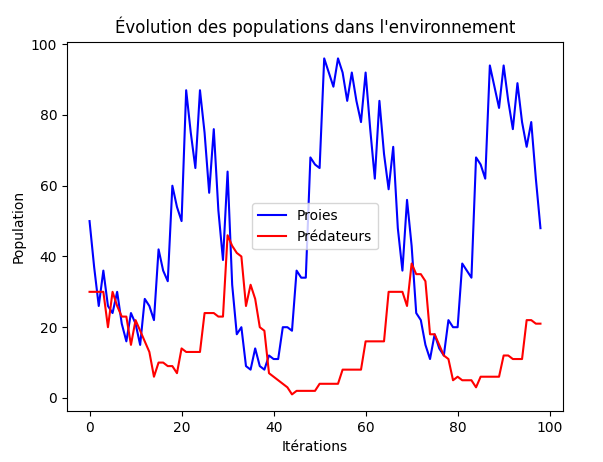
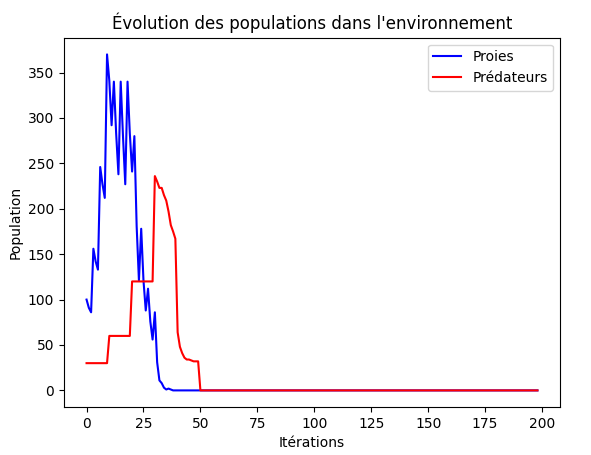
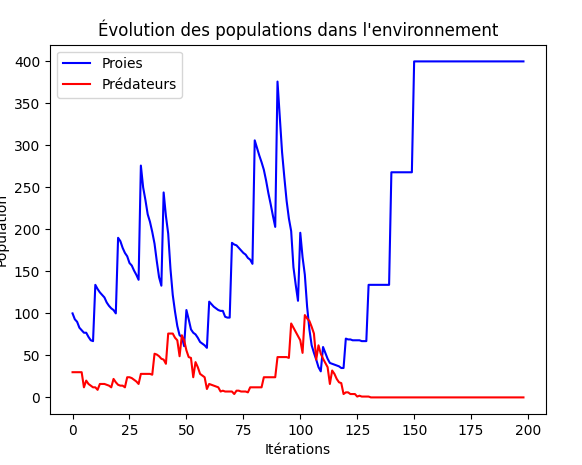
On observe quatre principaux types de résultats différents parmi les milliers de résultat obtenus
Bien qu'assez différents, ces résultats confirment une chose, l'équilibre qui se met en place pour qu'aucune des 2 espèce ne disparaissent est très fragile.
Possibilité d'agrandit la grille
Si l'on souhaite tester nos paramètres avec une grille plus grande tout en gardant une certaine cohérence entre les paramètres initiaux et la nouvelle taille de la grille, on effectue la formule suivante :
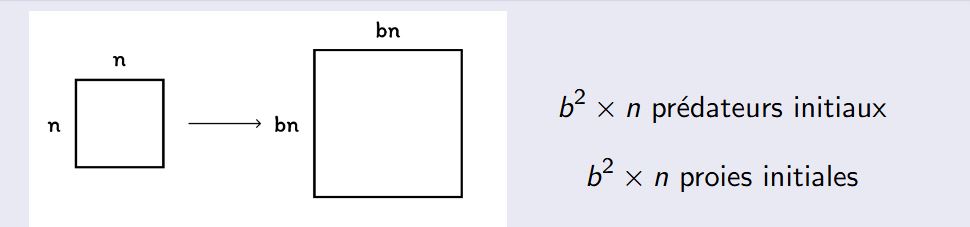
Si l'on fait ça par exemple avec les paramètres du troisième résultat qui était :
| Paramètre | Valeur |
|---|---|
| Taille | 20 x 20 |
| Itérations | 200 |
| Prédateurs initiaux | 30 |
| Proies initiales | 100 |
| n_faim | 5 |
| nr_pred | 6 |
| nr_proie | 10 |
On a maintenant une grille 100 × 100
donc b = 5
5 × 5 × 30 = 750 prédateurs initiaux
5 × 5 × 100 = 2500 proies initiales
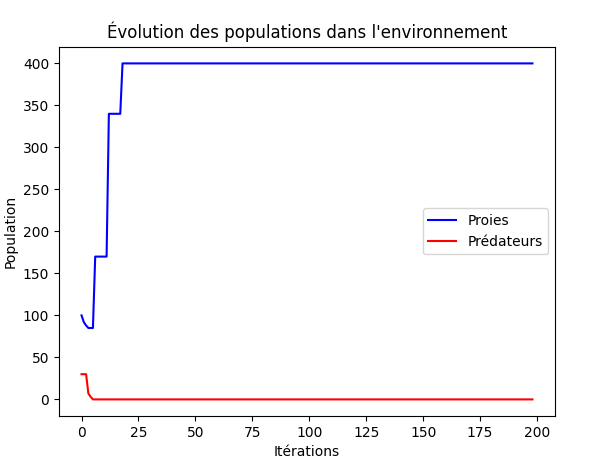
on obtient la grille suivante après simulation :
On obtient donc une courbe qui ressemble pratiquement à la même que pour une taille moins élevée avec les mêmes paramètres
Conclusion
On remarque donc que nous avons bien réussit à obtenir les mêmes résultats qu'avec les équations de Lotka-Volterra