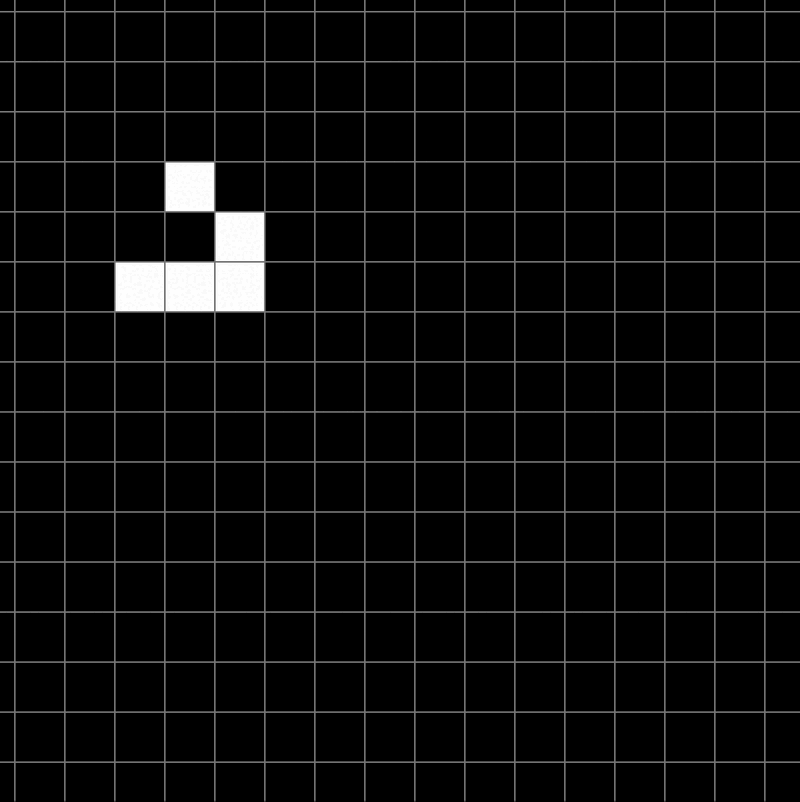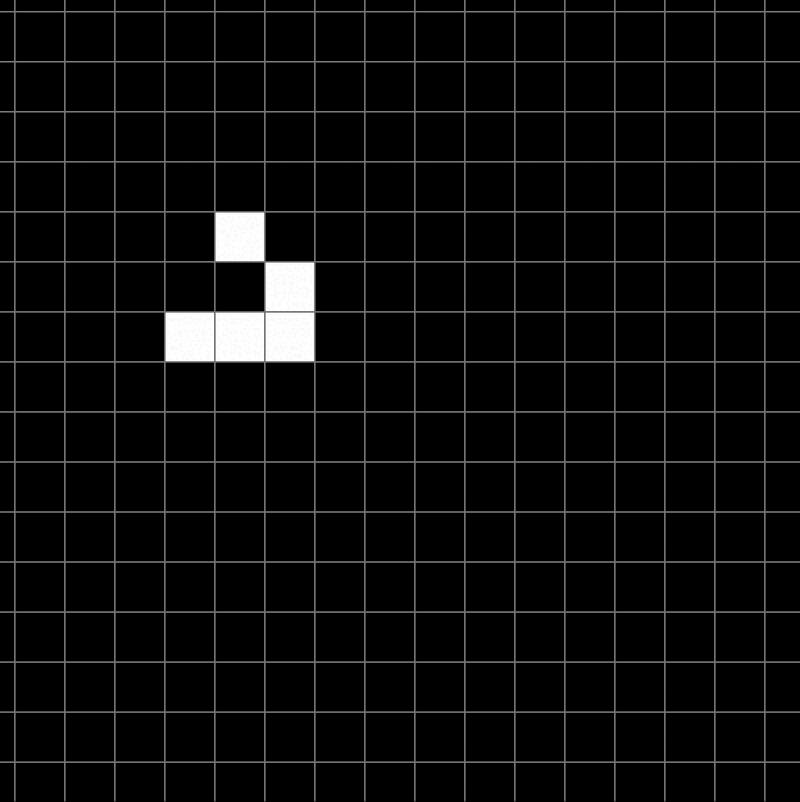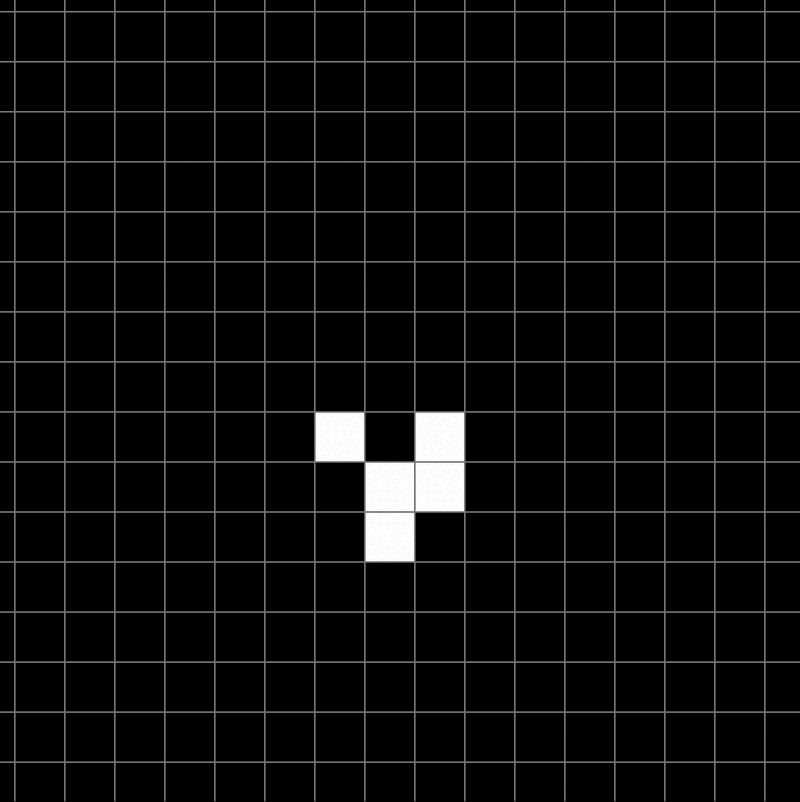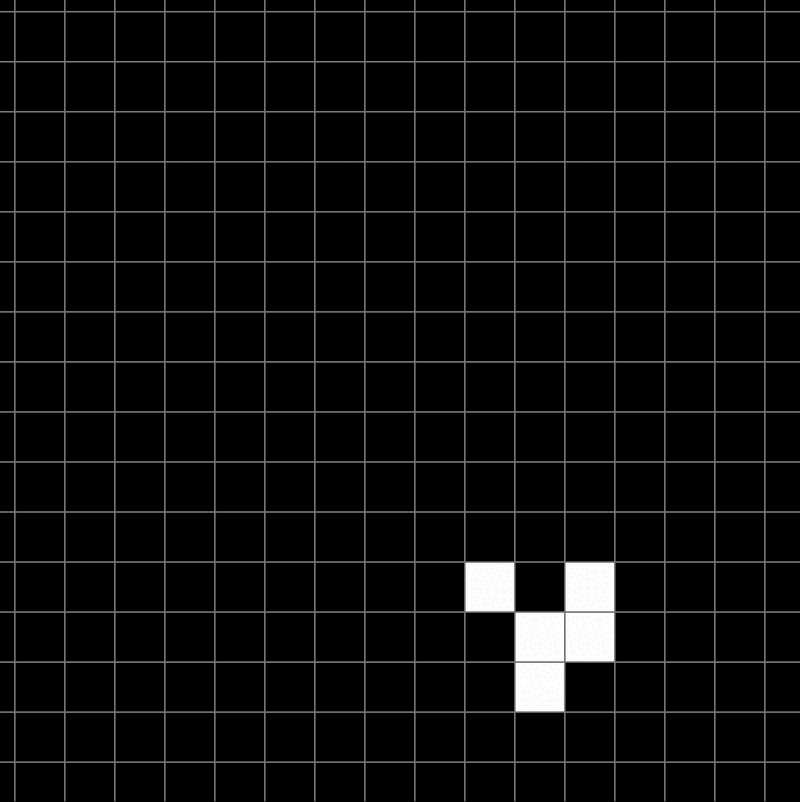Jeu de la vie

Introduction

Le jeu de la vie est un automate cellulaire inventé par le mathématicien John Conway en 1970. Il s'agit d'un système fondé sur des règles très simples qui déterminent l'évolution d'un ensemble de cellules sur une grille. Chaque cellule peut être dans l'un des deux états : vivante ou morte, et son état à la génération suivante dépend de celui de ses voisines.

Le contexte de sa création était celui de la recherche sur les systèmes dynamiques et l'émergence de la complexité à partir de règles élémentaires. Le jeu de la vie a ainsi ouvert la voie à l'étude des automates cellulaires et a inspiré de nombreux travaux en mathématiques, en informatique théorique, mais aussi en art numérique.

Malgré cette simplicité, le jeu de la vie donne naissance à des comportements étonnamment complexes et variés comme nous le verrons. Dans ce projet, nous allons explorer différentes manières d'implémenter le jeu de la vie, en commençant par une version simple sur une grille finie, puis en passant à une grille infinie optimisée, avant d'aborder l'approche en arbre.

Théorie et règles

Règles de base du jeu de la vie

A chaque génération, l'état de chaque cellule dépend de ses 8 voisins immédiats (représenté en vert):

Voisinage de Moore

• Une cellule morte naît si elle a exactement 3 voisins vivants

• Une cellules vivante meurt si elle a moins de 2 ou plus de 3 voisins vivants (sous-population ou surpopulation)

• Une cellule vivante survit si elle a exactement 2 ou 3 voisins.

Ces règles basiques s'appliquent sur toute la grille, toutes les cellules évoluent simultanément à chaque génération. La simplicité de ces règles est ce qui permet l'émergence de structures extrêmement complexes.

Exemples de comportements

• Les structures stationnaires : Ce sont des configurations qui restent figées dans le temps, sans changer d'état à travers les générations. Un exemple classique est le Block, un carré de 2x2 cellules vivantes qui reste stable tant qu’aucune cellule vivante ne vient interagir avec lui.

Block

Ruche

Miche

• Les vaisseaux : Ce sont des structures capables de se déplacer à travers la grille tout en conservant leur forme. Le plus connu est le Spaceship, un petit vaisseau qui se déplace horizontalement. Ces motifs montrent comment un mouvement global peut émerger de règles strictement locales.

Glider

Vaisseau

• Les oscillateurs : Il s’agit de structures qui reviennent périodiquement à leur configuration initiale après un certain nombre de générations. Le Pulsar est un oscillateur de période 3 : il alterne entre trois états différents avant de retrouver sa forme de départ.

Clignotant
Période : 2

Pulsar
Période : 3

• Gosper Glider Gun : C'est l'une des structures les plus importantes du jeu de la vie, elle est la base pour la logique. En effet, comme nous le verrons après, le Gosper Glider Gun va pouvoir devenir une source d'information dans une simulation logique prouvant ainsi que le jeu de la vie est Turing Complet.

Gosper Glider Gun

Turing-complet

Le concept de **Turing complétude** désigne la capacité d’un système à simuler **tout algorithme calculable**. Autrement dit, un dispositif Turing-complet peut, en principe, exécuter n’importe quel programme qu’un ordinateur classique permettrait de lancer.

Critères de Turing complétude dans le Jeu de la Vie

Pour démontrer que le Jeu de la Vie est Turing-complet, il faut montrer qu’il est possible d’y construire :

• Des portes logiques (AND, OR, NOT)

 Les gliders, canaux et collisions peuvent être arrangés de façon à reproduire le fonctionnement des portes de base d’un circuit logique.

• De la mémoire

 Des structures stables ou oscillantes (ex : des bascules ou « flip-flops ») permettent de stocker des bits d’information sous la forme de motifs rémanents.

• Un générateur d’impulsions

 Le **Gosper Glider Gun** produit en continu des gliders, servant à la fois d’« horloge » et de source de données.

• Des circuits complets

 En combinant portes logiques, mémoire et générateur d’impulsions, on peut construire un **processeur élémentaire** capable d’exécuter une suite d’instructions arbitraires.

Assemblage des composants

1. Propagation des gliders

  Des miroirs et réflecteurs sont capable de rediriger les gliders précisément pour acheminer les signaux.

2. Collisions contrôlées

  L’interaction de plusieurs gliders à un point donné réalise les opérations logiques

3. Stockage et bascules

  Des agencements stationnaires ou oscillants maintiennent un état « vivant » ou « mort » jusqu’à ce qu’une nouvelle impulsion vienne le modifier.

4. **Boucle de rétroaction**

  Les sorties peuvent être renvoyées en entrée pour créer des architectures séquentielles et des compteurs.

Vers un « CPU » dans le Jeu de la Vie

En empilant ces briques élémentaires, plusieurs projets ont déjà démontré la construction d’une **machine de Turing** complète au sein du Jeu de la Vie :

• Une **mémoire linéaire** où les gliders codent des bits le long d’une barre de cellules.
• Un **unité arithmétique et logique** (ALU) capable d’ajouter ou de comparer deux registres codés en impulsions de gliders.
• Un **contrôleur de instruction** séquencé par un réseau de Gosper Glider Guns, synchronisant lecture, calcul et écriture.

Ces réalisations confirment que, malgré ses règles locales et extrêmement simples, le Jeu de la Vie possède tous les ingrédients nécessaires pour être un modèle de calcul universel – en d’autres termes, **Turing complet**.

Implémentation sur une grille finie

Cette première version permet d'expérimenter les règles du jeu de la vie sur une grille simple. Elle est idéale pour bien comprendre le fonctionnement de base, même si elle montre vite ses limites sur des grandes tailles.

Structure de données utilisée

On utilise un tableau à deux dimensions pour stocker l’état de chaque cellule. Chaque élément vaut 0 (cellule morte) ou 1 (cellule vivante).

Initialisation et affichage de la grille

L'affichage se fait via Tkinter, en dessinant des rectangles pour chaque cellule selon son état.

# Initialisation d'une grille de dimensions définies par l'utilisateur
largeur = int(input("Largeur de la grille : "))
    hauteur = int(input("Hauteur de la grille : "))
    cases = []
    for i in range(largeur):
        cases_in = []
        for j in range(hauteur):
            cases_in += [0]
        cases += [cases_in]

Calcul des voisins et évolution des cellules

L'évolution d'une cellule s'effectue en comptant le nombre de voisins vivants autour d'elle et en appliquant les règles du jeu de la vie.

 def voisins_vivants(x, y):
    voisins = [(-1, -1), (-1, 0), (-1, 1), 
               (0, -1),           (0, 1),
               (1, -1),  (1, 0),  (1, 1)]
    nb_vivants = 0
    for dx, dy in voisins:
        nx, ny = x + dx, y + dy
        if 0 <= nx < hauteur and 0 <= ny < largeur:
            nb_vivants += cases[nx][ny]
    return nb_vivants

Cette fonction parcourt les 8 positions autour d'une cellule et compte les cellules vivantes en s'assurant de rester dans les limites de la grille.

Avantages et limites de l'approche naïve

• Simple à comprendre et à implémenter.

• Utiles pour des grilles de petite taille.

• Gaspillage de mémoire pour de grandes tailles.

• Inadapté lorsque la majorité des cellules restent mortes.

Implémentation sur une grille infinie

Pour simuler une grille infinie, on stocke uniquement les cellules vivantes, ce qui permet d'économiser de la mémoire et d'accélérer les calculs.

Principe de stockage par dictionnaire

Plutôt que d'utiliser un tableau complet, on utilise un dictionnaire où chaque clé représente les coordonnées d'une cellule vivante.

cases = {(x, y): 1, ...}

Gestion des cellules

Lors du calcul de la génération suivante, seules les cellules vivantes et leurs voisines potentielles sont considérées, ce qui permet d'ignorer rapidement les zones inactives.

for (x, y) in cases:
    candidats.add((x, y))
    for dx, dy in voisins:
        candidats.add((x + dx, y + dy))

Comparaison avec la grille finie

L'utilisation d'une dictionnaire pour stocker uniquement les cellules vivante est bien plus efficace en mémoire lorsque la densité de vie est faible. Elle est plus adapté aux grilles de grande taille, voire infinies, car elle évite de gérer un tableau complet.

Approche en arbre (quadtrees)

Un quadtree est une structure d’arbre qui divise récursivement la grille en 4 sous-régions. Cette approche est particulièrement adaptée pour simuler le jeu de la vie sur de très grandes grilles, voire infinies, lorsqu'une grande partie des cellules reste inactive.

Principe

• Subdivision de la grille : La grille est divisée en 4 quadrants, chacun pouvant être à son tour subdivisé en 4 sous-quadrants. Cette récursivité permet de représenter efficacement les zones homogènes, par exemple les régions totalement mortes.
• Compression  : Les régions ayant un état homogène (par exemple, totalement mortes) n'ont pas besoin d'être représentées en détail. Le quadtree regroupe ces zones en un seul noeud, réduisant ainsi la mémoire utilisée.
• Optimisation de l’évolution : Seules les zones actives, donc celles avec des cellules vivantes ou susceptibles de changer, sont simulées en détail. Ceci permet de gagner en performances en ignorant rapidement les grandes portions inactives.

Avantages de l'approche par quadtree

Les avantages sont nombreux, en voici certains :

• Mémoire : En ne stockant que les régions qu'il faut, l'approche par quadtree évite le gaspillage de mémoire associé aux grilles de grande taille.
• Performances améliorées : Le calcul se concentre uniquement sur les zones modifiées, ce qui accélère la simulation, notamment pour des configurations où la densité de cellules vivantes est faible.
• Extension à l’infini : Grâce à la représentation récursive et à la compression des zones inactives, cette méthode permet de simuler pratiquement une grille infinie.

Cette approche est souvent combinée avec l'algorithme Hashlife, qui exploite la redondance des configurations en mémorisant et réutilisant les sous-structures déjà calculées, permettant ainsi d'accélérer les simulations sur des périodes très longues.