« Carre de Polybe » : différence entre les versions
| Ligne 4 : | Ligne 4 : | ||
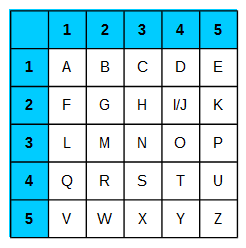
Le principe du carre de Polybe est relativement simple. Tous d’abord , nous allons créer une matrice carré d’ordre 5 dont chaque ligne et chaque colonne seront numérotées. Comme notre alphabets est constitué de 26 lettres et que notre matrice compte 25 cases, nous allons fusionné les lettres I/J. Il faut savoir qu’il est possible de fusionner d’autres lettres. |
Le principe du carre de Polybe est relativement simple. Tous d’abord , nous allons créer une matrice carré d’ordre 5 dont chaque ligne et chaque colonne seront numérotées. Comme notre alphabets est constitué de 26 lettres et que notre matrice compte 25 cases, nous allons fusionné les lettres I/J. Il faut savoir qu’il est possible de fusionner d’autres lettres. |
||
[[Fichier:Polybe.png]] |
[[Fichier:Polybe.png]] |
||
Pour chiffrer, il suffit d’associer une paire de (ligne, colonne) à chaque lettre d’un message. Pour dechiffrer, il suffit de faire le traitement inverse. |
Pour chiffrer, il suffit d’associer une paire de (ligne, colonne) à chaque lettre d’un message. Pour dechiffrer, il suffit de faire le traitement inverse. |
||
(Exemple :GIF) |
(Exemple :GIF) |
||
Version du 20 novembre 2016 à 15:54
Le carre de Polybe est une méthode ancienne de chiffrement par substitution. Actuellement, nous ne connaissons ni son inventeur, ni sa date de création. Le premier ouvrage connu qui traite de ce sujet s’appelle Histoire et a été rédigé vers -150 av-JC par l’historien grec Polybe (vers -200 à Mégalopolis – vers -120).
Principe général
Le principe du carre de Polybe est relativement simple. Tous d’abord , nous allons créer une matrice carré d’ordre 5 dont chaque ligne et chaque colonne seront numérotées. Comme notre alphabets est constitué de 26 lettres et que notre matrice compte 25 cases, nous allons fusionné les lettres I/J. Il faut savoir qu’il est possible de fusionner d’autres lettres.
Pour chiffrer, il suffit d’associer une paire de (ligne, colonne) à chaque lettre d’un message. Pour dechiffrer, il suffit de faire le traitement inverse. (Exemple :GIF)