« CSPRNG » : différence entre les versions
| (13 versions intermédiaires par 2 utilisateurs non affichées) | |||
| Ligne 10 : | Ligne 10 : | ||
'''L'attaque cryptanalytique directe''' correspond au fait de se baser sur une partie du flux de valeurs aléatoires fourni par un générateur afin de cerner en quoi il diffère d'un flux de valeurs parfaitement aléatoires. |
'''L'attaque cryptanalytique directe''' correspond au fait de se baser sur une partie du flux de valeurs aléatoires fourni par un générateur afin de cerner en quoi il diffère d'un flux de valeurs parfaitement aléatoires. |
||
'''L'attaque basée sur les inputs''' signifie que les inputs du générateur sont manipulées afin de l'attaquer. Par exemple, il est possible d'empêcher un générateur d'accumuler assez d'entropie pour ne pas dévoiler d'informations sur son état actuel. |
'''L'attaque basée sur les inputs''' signifie que les inputs du générateur sont manipulées afin de l'attaquer. Par exemple, il est possible d'empêcher un générateur d'accumuler assez d'entropie pour qu'il puisse ne pas dévoiler d'informations sur son état actuel. |
||
'''Les attaques partant d'un générateur compromis''' correspondent aux attaques qui utilisent la connaissance de l'état interne d'une générateur pour prédire ses prochaines valeurs ou les anciennes. |
'''Les attaques partant d'un générateur compromis''' correspondent aux attaques qui utilisent la connaissance de l'état interne d'une générateur pour prédire ses prochaines valeurs ou les anciennes. |
||
| Ligne 34 : | Ligne 34 : | ||
= Fortuna = |
= Fortuna = |
||
Fortuna est une évolution du générateur pseudo-aléatoire Yarrow. Il a été crée par Bruce SCHNEIER et Niels FERGUSON, et a été publié en 2003. Il a notamment été utilisé dans Windows 8. |
|||
Il reprend plusieurs idées de Yarrow, notamment ses 3 trois composants principaux, qui sont: l'accumulateur d'entropie, la seed et un générateur de nombre. |
|||
== L'accumulateur d'entropie == |
|||
La principale différence entre Fortuna et Yarrow réside dans ses accumulateurs d'entropie. |
|||
Dans Yarrow, nous avions deux pools qui stockaient les bits d'entropies que générait le système. Dans Fortuna, nous avons 32 pools (numéroté de P0 à P31). Un pool étant une chaîne de bits de taille non borné. |
|||
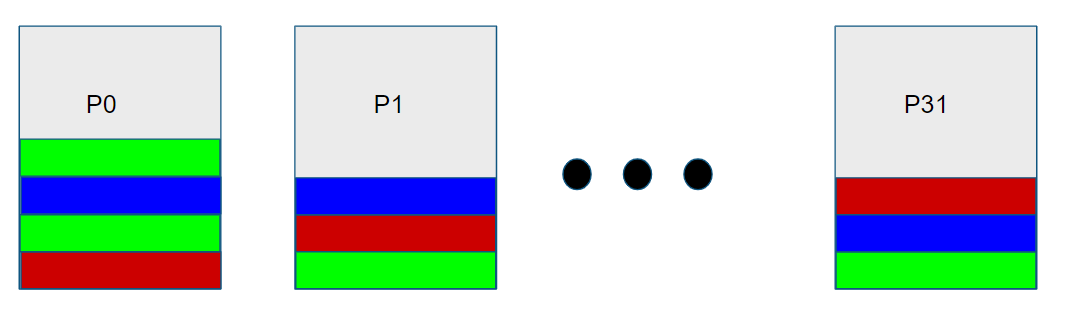
L'idée dans Fortuna est que les différentes sources d'entropies vont distribuer leurs bits d'entropie de façon circulaire entre les différentes pools. C'est-à-dire que prenons comme source d'entropie une saisie clavier, chaque touche va créer des bits d'entropie, les bits de la première touche iront dans la pool P0, puis ceux de la deuxième entrée iront dans P1, etc. De sorte que la 33ème entrée clavier créera des bits d'entropie stocké dans P0. |
|||
Comme illustré ci-dessous : Les différentes couleurs représentent les bits générés par les différentes sources d'entropies. |
|||
[[Fichier:EntropieCirculaire.PNG]] |
|||
Cela permet de répartir les bits générés par les sources d'entropie afin d'avoir des suites de bits plus aléatoires. |
|||
== Le mécansime de reseed == |
|||
Dans Fortuna, nous avons deux conditions pour déclencher le mécanisme du reseed: il faut que la pool P0 fasse au moins 128 bits et qu'il se soit passé un temps t depuis le dernier reseed. |
|||
La première condition a pour but d'assurer un certain nombre de bit d'entropie à chaque reseed, la seconde est là pour défendre le générateur des attaques par génération d’événement, ainsi même si l'attaquant génère beaucoup d’événement (et donc beaucoup de bit d'entropie, la pool contiendra quand même des bits qu'il ne connait pas). |
|||
Le mécanisme de reseed de Fortuna est très différent de celui de Yarrow, car il ne va pas utiliser une mais des pools. En effet, Fortuna va utiliser un compteur de reseed, qui va s’incrémente à chaque fois que l'on fait une opération de reseed. |
|||
Pour chaque reseed, nous allons vérifier les pools que nous allons utilisé. Pour qu'une pool soit utilisé, il faut que <math>2^i</math> (i étant le numéro de la pool) soit un diviseur du compteur de reseed. |
|||
P0 est donc utilisé à chaque reseed, P1 tous les deux reseeds, P2 tous les 4 reseeds, etc. |
|||
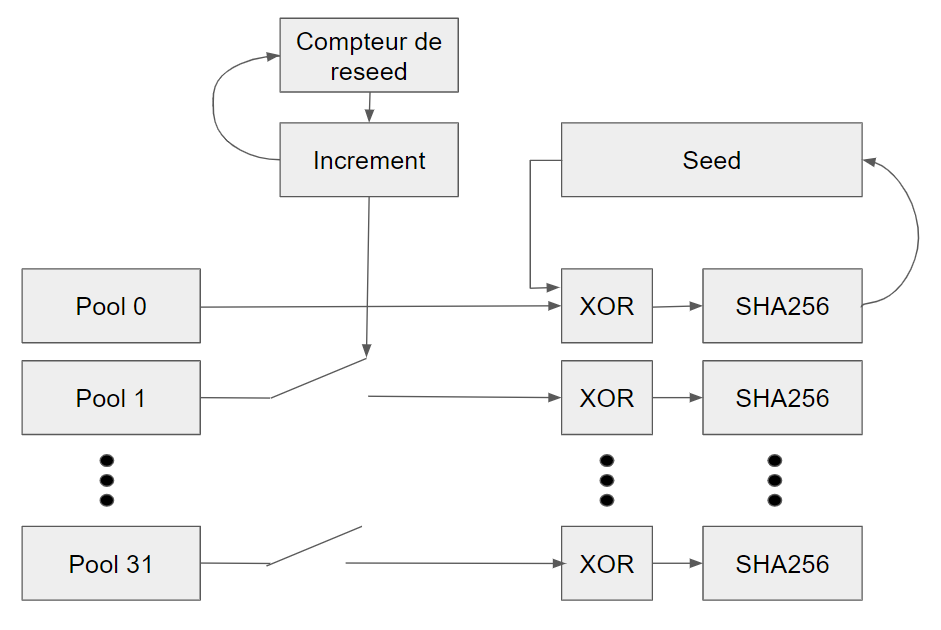
Une fois que toutes les pools sont sélectionnées pour le reseed, nous allons pour toutes effectuer un XOR avec la seed, puis le résultat du XOR sera passé dans une fonction de hachage (pour Fortuna nous utilisons SHA-256). |
|||
Le résultat de la fonction de hachage est utilisée comme nouvelle graine. |
|||
[[Fichier:Reseed.PNG]] |
|||
Une fois qu'une pool est utilisé, elle est vidée de ses bits d'entropies. |
|||
== Sécurité == |
|||
Si l’attaquant ne connait pas les sources d'entropies, même s'il génère lui-même beaucoup d'inputs, grâce au système circulaire, il ne serait pas en mesure de deviner P0 au prochain reseed. |
|||
Mais s'il en connait suffisamment, alors il pourra déterminer P0 pour le prochain reseed. Mais comme P1 est utilisé 2 fois moins que P0, P2 quatre fois moins, etc. ils sont tous d'autant plus gros que P0, donc si le reseed nécessite plus que P0, il y aura trop de données imprévisibles pour l'attaquant. |
|||
Indépendamment du nombre de faux événements généré par l’attaquant, ou combien d'événement il connaît, tant qu’il y a au moins une source d'événement aléatoire que l’attaquant ne peut pas prédire, il y aura toujours un accumulateur qui accueillera assez d’entropie pour le vaincre. |
|||
== Divers == |
|||
Il a été nommé Fortuna en hommage à la déesse romaine du hasard. |
|||
= Evolutions = |
= Evolutions = |
||
Même si Fortuna a été publié en 2003, le sujet est toujours ouvert car la problèmatique d'avoir des générateurs pseudo-aléatoires est omniprésente. |
|||
En 2014, un article est paru sur une manière d'améliorer Fortuna, pour le rendre robuste a plus de type d'attaques. |
|||
= Sources et Liens utiles = |
= Sources et Liens utiles = |
||
Dernière version du 24 novembre 2018 à 23:26
Les générateurs pseudo-aléatoires (PRNG) sont énormément utilisés en cryptographie, que ce soit pour générer des clés utilisées par des algorithmes de chiffrement symétriques, des salts pour perturber les logiciels de prédiction, des vecteurs d'initialisation utiles lors de l'utilisation de chiffrements par bloc en chaine, etc ...
Les cryptographes développent des algorithmes en se basant sur l'idée qu'on peut effectivement générer des nombres de manière imprévisible. Mais peut-on vraiment soutenir la robustesse d'un algorithme de chiffrement qui se base sur des nombres qu'un attaquant saurait deviner à l'avance ? Autrement dit, à quel point un algorithme peut être sécurisé, s'il est possible pour un attaquant de compromettre le générateur qu'il utilise ? Il apparait alors évidemment qu'un générateur se doit d'être lui aussi robuste et sécurisé.
Nous nous intéressons donc ici à certains modèles de générateurs pseudo-aléatoires crypto-sécurisés (CSPRNG).
Attaques de PRNG
On peut distinguer plusieurs types d'attaques de PRNGs:
L'attaque cryptanalytique directe correspond au fait de se baser sur une partie du flux de valeurs aléatoires fourni par un générateur afin de cerner en quoi il diffère d'un flux de valeurs parfaitement aléatoires.
L'attaque basée sur les inputs signifie que les inputs du générateur sont manipulées afin de l'attaquer. Par exemple, il est possible d'empêcher un générateur d'accumuler assez d'entropie pour qu'il puisse ne pas dévoiler d'informations sur son état actuel.
Les attaques partant d'un générateur compromis correspondent aux attaques qui utilisent la connaissance de l'état interne d'une générateur pour prédire ses prochaines valeurs ou les anciennes.
Yarrow
Yarrow désigne une famille de PRNG conçue par Bruce Schneier, John Kelsey et Niels Ferguson en 1999, dont le nom fait référence à d'anciens rites de divination.
Le modèle Yarrow se divise en 3 composants principaux : un accumulateur d'entropie, un mécanisme de reseed et un générateur à proprement parler (+ problème des anniversaires).
Accumulateur d'entropie
Yarrow comporte 2 boîtes (pool) dédiées à stocker les bits aléatoires issus de sources d'entropie. Typiquement, ces bits proviennent du système d'exploitation de la machine et du materiel en lui même (exemples : timing exacts de pression des touches, trajectoire du pointeur, ...). Pour les remplir, il va donc être question d'estimer la quantité d'entropie présente dans un apport. Cela dit, elles possèdent chacune une fonction d'estimation d'entropie qui lui est propre. L'une est qualifiée de rapide car la fonction d'estimation qui l'accompagne est plutôt optimiste quant à la quantité d'entropie qu'elle récupère dans un apport. L'autre est plus lente car plus conservatrice en entropie. Ces pool contiennent des données hashées, ce qui leur permet de perturber un attaquant qui voudrait obtenir de l'information dessus en contrôlant certaines sources d'entropie.
Reseed
Le reseed est l'action d'utiliser l'entropie stockée par les pool afin de modifier la clé privée du générateur. Ce mécanisme doit faire un compromis entre 2 approches. D'une part, il est préférable de reseed souvent afin d'empêcher un générateur compromis à un moment donné de divulguer trop d'informations. Mais d'autre part, on n'a pas toujours une quantité d'entropie suffisante pour être sûr qu'un attaquant ne puisse pas deviner quelles pourraient être les prochaines valeurs générées. C'est pourquoi utiliser trop souvent ce qu'on a accumulé peut mener à une faiblesse du système. C'est ici que l'idée d'avoir 2 pool rentre en jeu : la pool rapide permet d'effectuer des reseed assez régulièrement, et la pool lente permet de garder un taux "d'imprévisibilité" assez élevé.
Générateur
Pour générer des nombres pseudo aléatoires, Yarrow utilise un compteur qui sera incrémenté à chaque fois que l'on aura besoin d'une nouvelle valeur, puis encrypte ce compteur à l'aide d'un mécanisme de chiffrement par bloc qui utilise la clé du générateur. Le problème ici est que selon le problème des anniversaires, un générateur parfaitement aléatoire finira par produire des valeurs qu'il a déjà produite. L'utilisation d'un compteur comme mécanisme de génération empêche de reproduire ce phénomène, ce qui va à l'encontre du principe de génération d'une suite de valeur que l'on ne pourrait dissocier d'une suite de valeurs parfaitement aléatoires. C'est pourquoi il existe un mécanisme de "porte"/"gate" qui va régulièrement rechanger la clé (d'une autre manière que par un reseed) afin de permettre au générateur de renvoyer à l'occasion, des valeurs déjà produites.
Bilan
Bons points : Yarrow est un CSPRNG relativement performant et donc concrètement utilisable. Il peut être utilisé par des programmeurs non-expert en cryptographie en restant relativement sécurisé. Son niveau de sécurité dépend fondamentalement des mécanismes cryptographiques utilisés, et ces mécanismes peuvent être simplement remplacés par des choix contextuellement pertinents ou au file de l'évolution des outils cryptographiques.
Limites : Le niveau de sécurité de Yarrow est borné par le niveau de sécurité des mécanismes cryptographiques qu'il utilise : un attaquant capable de craquer son chiffrement pourra craquer le système qui utilise Yarrow. Ce modèle utilise un système d'estimation d'entropie, ce qui se révèle être un challenge au niveau de l'implémentation. A l'origine, il utilisait SHA-1 comme fonction de hachage qui est maintenant considérée comme obsolète.
Fortuna
Fortuna est une évolution du générateur pseudo-aléatoire Yarrow. Il a été crée par Bruce SCHNEIER et Niels FERGUSON, et a été publié en 2003. Il a notamment été utilisé dans Windows 8. Il reprend plusieurs idées de Yarrow, notamment ses 3 trois composants principaux, qui sont: l'accumulateur d'entropie, la seed et un générateur de nombre.
L'accumulateur d'entropie
La principale différence entre Fortuna et Yarrow réside dans ses accumulateurs d'entropie.
Dans Yarrow, nous avions deux pools qui stockaient les bits d'entropies que générait le système. Dans Fortuna, nous avons 32 pools (numéroté de P0 à P31). Un pool étant une chaîne de bits de taille non borné. L'idée dans Fortuna est que les différentes sources d'entropies vont distribuer leurs bits d'entropie de façon circulaire entre les différentes pools. C'est-à-dire que prenons comme source d'entropie une saisie clavier, chaque touche va créer des bits d'entropie, les bits de la première touche iront dans la pool P0, puis ceux de la deuxième entrée iront dans P1, etc. De sorte que la 33ème entrée clavier créera des bits d'entropie stocké dans P0.
Comme illustré ci-dessous : Les différentes couleurs représentent les bits générés par les différentes sources d'entropies.
Cela permet de répartir les bits générés par les sources d'entropie afin d'avoir des suites de bits plus aléatoires.
Le mécansime de reseed
Dans Fortuna, nous avons deux conditions pour déclencher le mécanisme du reseed: il faut que la pool P0 fasse au moins 128 bits et qu'il se soit passé un temps t depuis le dernier reseed. La première condition a pour but d'assurer un certain nombre de bit d'entropie à chaque reseed, la seconde est là pour défendre le générateur des attaques par génération d’événement, ainsi même si l'attaquant génère beaucoup d’événement (et donc beaucoup de bit d'entropie, la pool contiendra quand même des bits qu'il ne connait pas).
Le mécanisme de reseed de Fortuna est très différent de celui de Yarrow, car il ne va pas utiliser une mais des pools. En effet, Fortuna va utiliser un compteur de reseed, qui va s’incrémente à chaque fois que l'on fait une opération de reseed. Pour chaque reseed, nous allons vérifier les pools que nous allons utilisé. Pour qu'une pool soit utilisé, il faut que (i étant le numéro de la pool) soit un diviseur du compteur de reseed. P0 est donc utilisé à chaque reseed, P1 tous les deux reseeds, P2 tous les 4 reseeds, etc.
Une fois que toutes les pools sont sélectionnées pour le reseed, nous allons pour toutes effectuer un XOR avec la seed, puis le résultat du XOR sera passé dans une fonction de hachage (pour Fortuna nous utilisons SHA-256). Le résultat de la fonction de hachage est utilisée comme nouvelle graine.
Une fois qu'une pool est utilisé, elle est vidée de ses bits d'entropies.
Sécurité
Si l’attaquant ne connait pas les sources d'entropies, même s'il génère lui-même beaucoup d'inputs, grâce au système circulaire, il ne serait pas en mesure de deviner P0 au prochain reseed. Mais s'il en connait suffisamment, alors il pourra déterminer P0 pour le prochain reseed. Mais comme P1 est utilisé 2 fois moins que P0, P2 quatre fois moins, etc. ils sont tous d'autant plus gros que P0, donc si le reseed nécessite plus que P0, il y aura trop de données imprévisibles pour l'attaquant.
Indépendamment du nombre de faux événements généré par l’attaquant, ou combien d'événement il connaît, tant qu’il y a au moins une source d'événement aléatoire que l’attaquant ne peut pas prédire, il y aura toujours un accumulateur qui accueillera assez d’entropie pour le vaincre.
Divers
Il a été nommé Fortuna en hommage à la déesse romaine du hasard.
Evolutions
Même si Fortuna a été publié en 2003, le sujet est toujours ouvert car la problèmatique d'avoir des générateurs pseudo-aléatoires est omniprésente. En 2014, un article est paru sur une manière d'améliorer Fortuna, pour le rendre robuste a plus de type d'attaques.
Sources et Liens utiles
Article Yarrow (1999)
Article Fortuna (2003)
Généralisation de Fortuna (2014)