« Cryptanalyse d'Enigma » : différence entre les versions
| (14 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 14 : | Ligne 14 : | ||
[[Fichier:Fonctionnement.png|center]] |
[[Fichier:Fonctionnement.png|center]] |
||
| ⚫ | |||
'''Histoire''': Les premières versions commerciales d'Enigma remontent au début des années 1920. |
'''Histoire''': Les premières versions commerciales d'Enigma remontent au début des années 1920. |
||
Le cryptage de la machine apparaît alors comme très sûr, '''impossible à casser'''. |
Le cryptage de la machine apparaît alors comme très sûr, '''impossible à casser'''. |
||
| Ligne 31 : | Ligne 31 : | ||
'''Été 1939''' : Les Polonais font part de leur découvertes aux alliés. |
'''Été 1939''' : Les Polonais font part de leur découvertes aux alliés. |
||
| ⚫ | |||
== La cryptanalyse == |
== La cryptanalyse == |
||
| Ligne 64 : | Ligne 63 : | ||
Au risque de causer un court circuit, une lettre ne peut être encodée en elle même. C’est une grosse faiblesse introduit par le réflecteur, essentiel à la décryption du message. |
Au risque de causer un court circuit, une lettre ne peut être encodée en elle même. C’est une grosse faiblesse introduit par le réflecteur, essentiel à la décryption du message. |
||
[[Fichier: |
[[Fichier:Circuit.gif|center]] |
||
Voici un message encodé avec Enygma, où l’on peut observer ce phénomène: |
Voici un message encodé avec Enygma, où l’on peut observer ce phénomène: |
||
[[Fichier: |
[[Fichier:msgCode.png|center]] |
||
==== 3. Pas régulier des roues ==== |
==== 3. Pas régulier des roues ==== |
||
| Ligne 80 : | Ligne 78 : | ||
1 sur 17 (5.9%) pour un message en Allemand |
1 sur 17 (5.9%) pour un message en Allemand |
||
[[Fichier: |
[[Fichier:decode.png|center]] |
||
Par la suite, on peut établir une “chaîne” des positions de rotors en prenant la position initiale de chaque message et la distance entre les chaînes : [[Fichier: |
Par la suite, on peut établir une “chaîne” des positions de rotors en prenant la position initiale de chaque message et la distance entre les chaînes : [[Fichier:distanse.png]] |
||
Enfin, on tente de faire correspondre cette chaîne avec les lettres des trois rotors. Ainsi, on déterminera quel est le rotor rapide du jour et sa position initiale, divisant ainsi le nombre de possibilités par 26. |
Enfin, on tente de faire correspondre cette chaîne avec les lettres des trois rotors. Ainsi, on déterminera quel est le rotor rapide du jour et sa position initiale, divisant ainsi le nombre de possibilités par 26. |
||
[[Fichier: |
[[Fichier:demo.png|center]] |
||
==== 4. Double pas d’un rotor ==== |
==== 4. Double pas d’un rotor ==== |
||
| Ligne 94 : | Ligne 91 : | ||
==== 5. Double entraîneur ==== |
==== 5. Double entraîneur ==== |
||
[[Fichier: |
[[Fichier:bague2.png|center]] |
||
Le fait d’apporter un deuxième entraîneur aux rotors était censé augmenter la complexité de codage, pourtant étant donné que 2 divise 26, ces deux entraîneurs engendrent des saut de la moitié des combinaisons possibles. Comme l’erreur est répétée deux fois, les combinaisons sont divisées par 4. |
Le fait d’apporter un deuxième entraîneur aux rotors était censé augmenter la complexité de codage, pourtant étant donné que 2 divise 26, ces deux entraîneurs engendrent des saut de la moitié des combinaisons possibles. Comme l’erreur est répétée deux fois, les combinaisons sont divisées par 4. |
||
| Ligne 104 : | Ligne 101 : | ||
La complexité d’un tableau d’échange sans paires est de <math>26^{26}</math>... |
La complexité d’un tableau d’échange sans paires est de <math>26^{26}</math>... |
||
[[Fichier: |
[[Fichier:tableau.jpg|center]] |
||
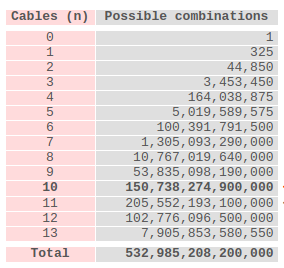
Le tableau des complexités en fonction du nombre de câbles ci-dessous nous indique qu’utiliser 11 câbles est optimal si un nombre fixe de câbles devait être utilisé. Il a pourtant été fixé à 10 par les allemands. Si ce nombre n’avait pas été fixé, il aurait atteint le nombre '''Total''' en bas de ce tableau. |
Le tableau des complexités en fonction du nombre de câbles ci-dessous nous indique qu’utiliser 11 câbles est optimal si un nombre fixe de câbles devait être utilisé. Il a pourtant été fixé à 10 par les allemands. Si ce nombre n’avait pas été fixé, il aurait atteint le nombre '''Total''' en bas de ce tableau. |
||
[[Fichier: |
[[Fichier:total.png|center]] |
||
==== 7. Les messages de tests ==== |
==== 7. Les messages de tests ==== |
||
| Ligne 114 : | Ligne 111 : | ||
Il arrivait que les allemands envoient un message de test à leur points de communication. Ce message de tests contenait une suite de lettres identiques. Voici un crypté dont le message clair ne contient que des “T”: |
Il arrivait que les allemands envoient un message de test à leur points de communication. Ce message de tests contenait une suite de lettres identiques. Voici un crypté dont le message clair ne contient que des “T”: |
||
[[Fichier: |
[[Fichier:fullT.png|center]] |
||
Comme on peut le constater, ce message ne contient aucun “T” (voir la vulnérabilité n°1), ce qui indique qu’il est constitué essentiellement de cette lettre. Il devient ainsi aisé de déterminer la position initiale des rotors du jour. |
Comme on peut le constater, ce message ne contient aucun “T” (voir la vulnérabilité n°1), ce qui indique qu’il est constitué essentiellement de cette lettre. Il devient ainsi aisé de déterminer la position initiale des rotors du jour. |
||
Dernière version du 25 novembre 2018 à 15:55
Introduction
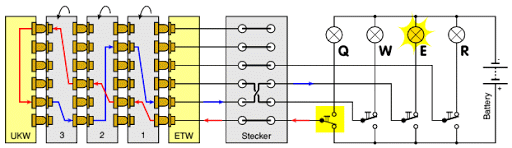
Le principe de fonctionnement de l'Enigma est à la fois simple et astucieux. A chaque fois que l'on presse une lettre, un circuit électrique est fermé, et s'éclaire une ampoule qui correspond à la lettre codée. Le circuit qui est fermé dépend de la position des rotors. A chaque lettre frappée, un ou plusieurs des rotors mobiles tourne, changeant la substitution qui sera opérée à la prochaine touche pressée. De plus, le chiffrage est réversible : si en tapant A vous codez D, si vous aviez tapé D, vous auriez codé A. Ainsi, si le commandement allemand et le sous-marin ont le même réglage de départ, il suffit à l'opérateur du sous-marin de taper directement le message codé pour obtenir le message clair. Les Allemands avaient donc diffusé dans leurs services des carnets de code permettant de réactualiser chaque jour à minuit les machines, par la position initiale des rotors. Ces carnets de code étaient valables un mois.
La machine était constituée :
- d'un clavier alphabétique
- d'un tableau de connexion
- d’un rotor d’entrée
- de 3 rotors mobiles à 26 positions
- d'un rotor de retour à 26 positions (le réflecteur)
- d'un tableau de 26 ampoules correspondant aux 26 lettres de l'alphabet.
Histoire: Les premières versions commerciales d'Enigma remontent au début des années 1920. Le cryptage de la machine apparaît alors comme très sûr, impossible à casser. Six ans après, plusieurs pays tentent de percer les mystères d'Enigma. Mais les mathématiciens américains, britanniques et français échouent. Les dates importantes:
1920 : Première version commerciale d'Enigma.
1926 : Enigma considérée comme inviolable. La marine allemande chiffre ses transmissions avec une nouvelle version d’Enigma.
1929 : Les Polonais interceptent une version militaire d’Enigma.
1938 : Bombe cryptologique Polonaise (2h pour décrypter un message).
Début 1939 : Les Allemands complexifient leur système d’encryption, la bombe devient inutile.
Été 1939 : Les Polonais font part de leur découvertes aux alliés.
La cryptanalyse
En 1928, les Polonais interceptent une version commerciale de la machine Enigma. S’en suit alors le début de sa cryptanalyse. La cryptanalyse d'Enigma, c'est le décryptage de messages chiffrés par la machine à coder allemande Enigma.
Chaque mois, les points de communication allemands recevaient un carnet journalier de paramètres pour leur machine Enigma. Voici la démarche effectuée chaque jour par l’armée allemande pour paramétrer Enigma:
- Changement des positions des rotors (exemple: ABC)
- Changement de la bague des rotors (qui entraîne les autres rotors)
- Permutations des fiches du tableau de connexions (10 permutations)
- Le chiffreur tape deux fois une clé de trois chiffres choisie arbitrairement, et note le resultat (exemple: RTERTE = AZDCFR) qu’il mettra en en-tête de chaque message
- Il positionne ensuite les rotors sur la position de sa clé (RTE)
- Il peut maintenant commencer à taper ses messages
Les vulnérabilités d’Enigma:
1. L’encodage de la clé en préambule
Entre deux machines enigma de même marque, les circuits d’encryption des rotors ne diffèrent. Il était donc important pour les polonais de se procurer le “chemin d’encryption” des rotors afin de déterminer la clé et les connexions du tableau.
C’est le mathématicien Marian Rejewski qui découvre un moyen mathématique de retrouver ces paramètres essentiels.
Il découvre la répétition de la clé dans le préambule du message, ce qui lui permit de réduire son espace de recherche sur le câblage des rotors. Comme la clé était chiffrée deux fois et faisait toujours trois caractères, il devenait possible de déterminer comment les rotors étaient configurés: Sur la clé cryptée “AKZSED”, les rotors ont produit pour la même lettre A et S, K et E, Z et D.
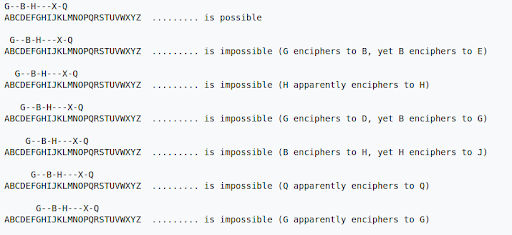
2. Une lettre ne s’encode jamais en elle même
Au risque de causer un court circuit, une lettre ne peut être encodée en elle même. C’est une grosse faiblesse introduit par le réflecteur, essentiel à la décryption du message.
Voici un message encodé avec Enygma, où l’on peut observer ce phénomène:
3. Pas régulier des roues
Les roues avancent régulièrement. Aucune lettre n’est sautée. Cette régularité permet d’introduire une faille appelée “Banburismes”.
Objectif: Trouver la position initiale du rotor “rapide” du jour en maximisant l’indice de coïncidence entre des paires de messages cryptés par différentes machines:
1 sur 17 (5.9%) pour un message en Allemand
Par la suite, on peut établir une “chaîne” des positions de rotors en prenant la position initiale de chaque message et la distance entre les chaînes : ![]() Enfin, on tente de faire correspondre cette chaîne avec les lettres des trois rotors. Ainsi, on déterminera quel est le rotor rapide du jour et sa position initiale, divisant ainsi le nombre de possibilités par 26.
Enfin, on tente de faire correspondre cette chaîne avec les lettres des trois rotors. Ainsi, on déterminera quel est le rotor rapide du jour et sa position initiale, divisant ainsi le nombre de possibilités par 26.
4. Double pas d’un rotor
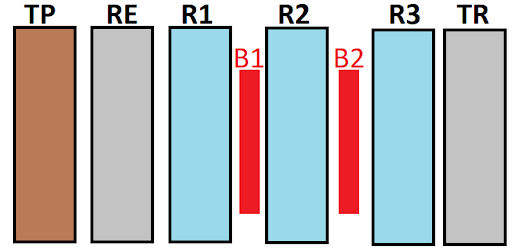
Sur certaines machines, un défaut de conception a engendré un double pas du rotor R2 à chaque fois que le rotor R1 effectue un tour. Cela a eu pour effet de diviser par deux les possibilités d’encryption d’enigma car 2 est un multiple de 26, donc une lettre sur deux était sautée.
5. Double entraîneur
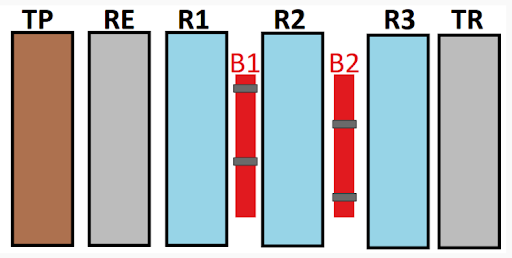
Le fait d’apporter un deuxième entraîneur aux rotors était censé augmenter la complexité de codage, pourtant étant donné que 2 divise 26, ces deux entraîneurs engendrent des saut de la moitié des combinaisons possibles. Comme l’erreur est répétée deux fois, les combinaisons sont divisées par 4.
6. Tableau de permutations
Une permutation par paire est obligatoire pour rendre l’encodage symétrique (décryptable). Cependant, il réduit grandement le nombre de possibilités. Voici la formule qui permet de calculer la complexité d’un tableau par paires, où n est le nombre de câbles utilisé:
La complexité d’un tableau d’échange sans paires est de ...
Le tableau des complexités en fonction du nombre de câbles ci-dessous nous indique qu’utiliser 11 câbles est optimal si un nombre fixe de câbles devait être utilisé. Il a pourtant été fixé à 10 par les allemands. Si ce nombre n’avait pas été fixé, il aurait atteint le nombre Total en bas de ce tableau.
7. Les messages de tests
Il arrivait que les allemands envoient un message de test à leur points de communication. Ce message de tests contenait une suite de lettres identiques. Voici un crypté dont le message clair ne contient que des “T”:
Comme on peut le constater, ce message ne contient aucun “T” (voir la vulnérabilité n°1), ce qui indique qu’il est constitué essentiellement de cette lettre. Il devient ainsi aisé de déterminer la position initiale des rotors du jour.
8. Cillies
Encrypter un même message avec deux machines différentes, une au cryptage faible et l’autre au cryptage fort, comme la météo du jour par exemple. Les alliés cassaient d’abord la clé simple pour obtenir le message clair. La décryption de la clé difficile devenait plus simple car le clair était disponible. Une position initiale cassée = une journée complète de décodée comme vu en introduction.
9. Erreurs humaines
Ne jamais changer la clé d’encryption, encoder un même message avec des méthodes différentes, ne pas mettre à jour le tableau de permutations ou ne pas échanger les rotors de place. Toutes ces petites erreurs ont engendré de lourdes vulnérabilités dans le système d’encryption d’Enygma.
Conclusion
Beaucoup de fonctionnalités semblaient ajouter de la complexité à l’encryption alors qu’en définitive elles ont rendu la tâche plus facile aux cryptologues. Le réflecteur, la symétrie du tableau de permutations et les erreurs humaines ont rendu la cryptanalyse possible alors qu’elle était considérée comme impossible en 1926.