« Les réseaux euclidiens » : différence entre les versions
| (8 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 129 : | Ligne 129 : | ||
[[Fichier:Réseau_euclidien_chiffrage.png|left|700px|Chiffrage]] |
[[Fichier:Réseau_euclidien_chiffrage.png|left|700px|Chiffrage]] |
||
=== Le déchiffrement=== |
=== Le déchiffrement=== |
||
Pour le déchiffrement, il suffit de retrouver le point représenté par le vecteur d grâce à notre clé privée. Pour cela on utilise l'algorithme de Babai qui va paver l'espace avec au centre de chaque pavé un point du réseau. Et ensuite permettre de retrouver le point du pavé (le point du réseau représenté par le vecteur d) où se trouve notre vecteur message chiffré. |
Pour le déchiffrement, il suffit de retrouver le point représenté par le vecteur d grâce à notre clé privée. Pour cela on utilise l'algorithme de Babai qui va paver l'espace avec au centre de chaque pavé un point du réseau. Et ensuite permettre de retrouver le point du pavé (le point du réseau représenté par le vecteur d) où se trouve notre vecteur message chiffré. |
||
Un fois le vecteur d retrouvé on le soustrait au vecteur message |
Un fois le vecteur d retrouvé on le soustrait au vecteur message chiffré. |
||
def dechiffre(Secret, m_chiffré): |
def dechiffre(Secret, m_chiffré): |
||
| Ligne 138 : | Ligne 168 : | ||
m = m_chiffré - d |
m = m_chiffré - d |
||
return m |
return m |
||
=== Algorithme de Babai=== |
=== Algorithme de Babai=== |
||
| Ligne 205 : | Ligne 234 : | ||
== Robustesse == |
== Robustesse == |
||
| ⚫ | |||
Bien entendu un réseau euclidien en dimension 2, n'est pas assez robuste, cependant le temps pour réduire un réseau euclidien, c'est à dire trouver une bonne base d'un réseau, croît de manière exponentielle, plus le nombre de dimension augmente. A partir de 80 dimensions, il faut déjà mettre un certain effort pour arriver à ses fins. Les records sur clusters atteignent non sans mal, 130 dimensions actuellement. On considère qu'avec 200 ou 250 dimensions les réseaux euclidiens sont assez robuste puisque l'on estime le temps de calculs en milliards d'années pour déchiffrer le message chiffré. |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
Il y a plusieurs problèmes algorithmiques dans les réseaux : |
Il y a plusieurs problèmes algorithmiques dans les réseaux : |
||
| Ligne 218 : | Ligne 245 : | ||
Pour réduire un réseau euclidien de dimension 2, il existe une méthode simple et efficace très similaire à l'algorithme d'Euclide pour calculer le PGCD de deux entiers. Comme avec l'algorithme euclidien, la méthode est itérative, à chaque étape, le plus grand des deux vecteurs est réduit en ajoutant ou en soustrayant un multiple entier du plus petit vecteur. |
Pour réduire un réseau euclidien de dimension 2, il existe une méthode simple et efficace très similaire à l'algorithme d'Euclide pour calculer le PGCD de deux entiers. Comme avec l'algorithme euclidien, la méthode est itérative, à chaque étape, le plus grand des deux vecteurs est réduit en ajoutant ou en soustrayant un multiple entier du plus petit vecteur. |
||
Cependant le temps croît de manière exponentielle quand le nombre de |
Cependant le temps croît de manière exponentielle quand le nombre de dimensions augmente. A partir de 80 dimensions, un effort considérable est déjà requis. Les records sur clusters atteignent avec difficultés, 130 dimensions. On considère qu'avec 200 ou 250 dimensions les réseaux euclidiens sont assez robustes puisque l'on estime le temps de calculs en milliards d'années. |
||
== Un jeu sur les reseaux euclidiens : Cryptris== |
== Un jeu sur les reseaux euclidiens : Cryptris== |
||
| Ligne 227 : | Ligne 254 : | ||
== Chiffrement homomorphe== |
== Chiffrement homomorphe== |
||
Le chiffrement homomorphe permet d'effectuer une ou plusieurs opérations sans |
Le chiffrement homomorphe permet d'effectuer une ou plusieurs opérations sans la nécessité d'accéder aux données sensibles en les déchiffrant. |
||
Pour |
Pour toutes opérations Op et pour tous messages m1 et m2, effectuer l'opération sur les messages cryptés par la méthode C et ensuite déchiffés par D est équivalent au résultat de l'opération sur les deux messages clairs : |
||
<br/> |
<br/> |
||
<br/> |
<br/> |
||
| Ligne 234 : | Ligne 261 : | ||
<br/> |
<br/> |
||
<br/> |
<br/> |
||
Prenons l'exemple d'Alice. Alice souhaite pouvoir effectuer des opérations sur deux données sensibles mais elle ne possède pas la puissance de calcul nécessaire pour l'effectuer. Elle souhaite donc demander à un organisme tiers de procéder aux calculs sur ses données. Cependant, les données à traiter sont sensibles et Alice ne fait pas confiance en cet organisme. Elle va donc |
Prenons l'exemple d'Alice. Alice souhaite pouvoir effectuer des opérations sur deux données sensibles mais elle ne possède pas la puissance de calcul nécessaire pour l'effectuer. Elle souhaite donc demander à un organisme tiers de procéder aux calculs sur ses données. Cependant, les données à traiter sont sensibles et Alice ne fait pas confiance en cet organisme. Elle va donc utiliser un chiffrement homomorphe et envoyer des données chiffrées à l'organisme qui pourra ainsi calculer et renvoyer le résultat, encore chiffré, à Alice. Alice pourra alors déchiffrer le message pour obtenir le résultat de l'opération sur ses données sensibles grâce aux propriétés du chiffrement homomorphe. |
||
[[File:alice.png|center|800px|Exemple Alice]] |
[[File:alice.png|center|800px|Exemple Alice]] |
||
| Ligne 263 : | Ligne 290 : | ||
En effet, alors que la taille des clés de chiffrement de la méthode RSA se situe entre 128 à 512 octets, celle des clés du cryptage par réseaux euclidiens représente plusieurs méga-octets et reste donc beaucoup trop lourde aujourd'hui pour être viable. |
En effet, alors que la taille des clés de chiffrement de la méthode RSA se situe entre 128 à 512 octets, celle des clés du cryptage par réseaux euclidiens représente plusieurs méga-octets et reste donc beaucoup trop lourde aujourd'hui pour être viable. |
||
De plus, il faut savoir que l'addition et la multiplication homomorphe sont 1000 fois plus |
De plus, il faut savoir que l'addition et la multiplication homomorphe sont 1000 fois plus longues que les opérations classiques. |
||
Ces deux inconvénients, bien qu'ils paraissent insignifiant, constituent aujourd'hui le problème majeur du chiffrement. De nombreux chercheurs dont Craig Gentry, le premier à avoir écrit une thèse sur cette méthode de chiffrement en 2009, travaille sur la réduction de la taille des clés ainsi que sur la performance pour effectuer les opérations homomorphes. |
Ces deux inconvénients, bien qu'ils paraissent insignifiant, constituent aujourd'hui le problème majeur du chiffrement. De nombreux chercheurs dont Craig Gentry, le premier à avoir écrit une thèse sur cette méthode de chiffrement en 2009, travaille sur la réduction de la taille des clés ainsi que sur la performance pour effectuer les opérations homomorphes. |
||
Dernière version du 26 novembre 2018 à 00:25
Un réseau euclidien est un objet mathématique qui a été utilisé premièrement pour la cryptanalyse. C'est Miklos Ajtai qui a démontré que les réseaux euclidiens peuvent servir de base solide pour la cryptologie. Une des caractéristiques remarquables des problèmes de réseaux est qu'il n'existe pas d'instances faibles, différemment du cas RSA où l'utilisation de certains nombres premiers entraînerait une factorisation simple pour les calculateurs actuels. De plus, ces problèmes sont reconnus comme étant difficile. Il n'est donc pas possible de les résoudre efficacement en un temps convenable même avec un ordinateur quantique. Les crypto-systèmes se basant sur cet objet mathématique sont donc actuellement source de nombreuses études, en particulier pour la caractéristique homomorphe de ce chiffrement qui permet d'effectuer des calculs directement sur les données chiffrées. Cela peut garantir la sécurité dans de nombreuses applications comme par exemple lors de calculs effectués sur les services cloud.
Introduction
Un ordinateur quantique, ou calculateur quantique, utilise les propriétés de la physique quantique comme l'intrication quantique et la superposition quantique. Cet ordinateur n'est pas basé sur des bits ayant soit un état 0 soit un état 1, mais est basé sur des qubits, l'unité de stockage d'information quantique, qui est composé d'une superposition de deux états de base : 0 et 1. Ainsi ce type d'ordinateur peut calculer 16 fois plus rapidement qu'un ordinateur à 4 bits, seulement avec 4 qubits et la puissance est doublée a chaque fois que l'on rajoute un qubit.
Ce type d'ordinateur peut aujourd'hui représenter une menace envers les chiffrements actuellement utilisés En effet, le chiffrement RSA se base sur des nombres premiers très grands pour sécuriser les données. Pour décoder RSA, il faut utiliser la décomposition en facteurs premiers. Aujourd'hui, aucun algorithme "classique" permet de déchiffrer RSA dans un temps raisonnable (Polynomiale).
Mais l'algorithme de Shor, algorithme basé sur la physique quantique pourrait effectuer cette décomposition beaucoup plus rapidement et rendrait inefficace les cryptographies actuelles si ce dernier était implémenté sur un calculateur quantique.
L'intérêt aujourd'hui est donc de trouver une solution à cette futur menace pas si lointaine. De nombreuses entreprises travaillent sur le sujet dont IBM qui est actuellement sur un nouveau type de chiffrement basé sur les réseaux euclidiens afin de remplacer les méthodes de chiffrement utilisées de nos jours .
Les principes de base du réseau euclidien
Pour faciliter la compréhension ainsi que la représentation géométrique d'un réseau, nous partirons du principe que le message est constitué de 2 digits résultant ainsi d'une dimension égale à 2, plus facile à représenter dans ce wiki
Un réseau euclidien est "ensemble de points régulièrement répartis sur une dimension n" ou avec des termes plus mathématique, il s'agit d'un sous-groupe discret d'un espace vectoriel euclidien.
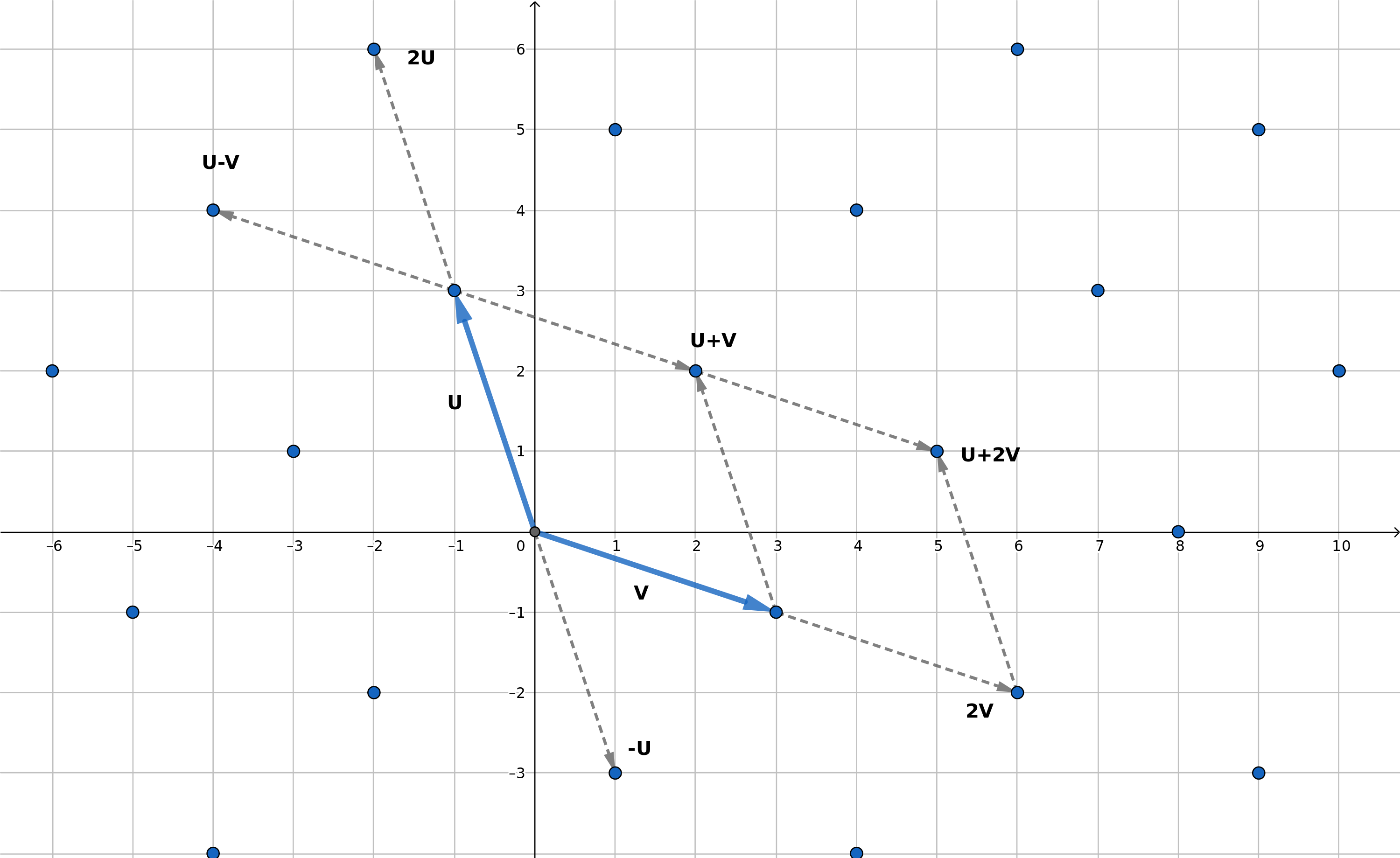
Voici la représentation d'un réseau euclidien de dimension 2. Comme le nombre de points est infini, il serait difficile de faire la liste de ces points. Ils sont donc représentés par une base, ici (O, u, v). Les points ont donc des coordonnées correspondant à la base de notre réseau euclidien.
Vecteur u :
Vecteur v :
Base :
Bases différentes
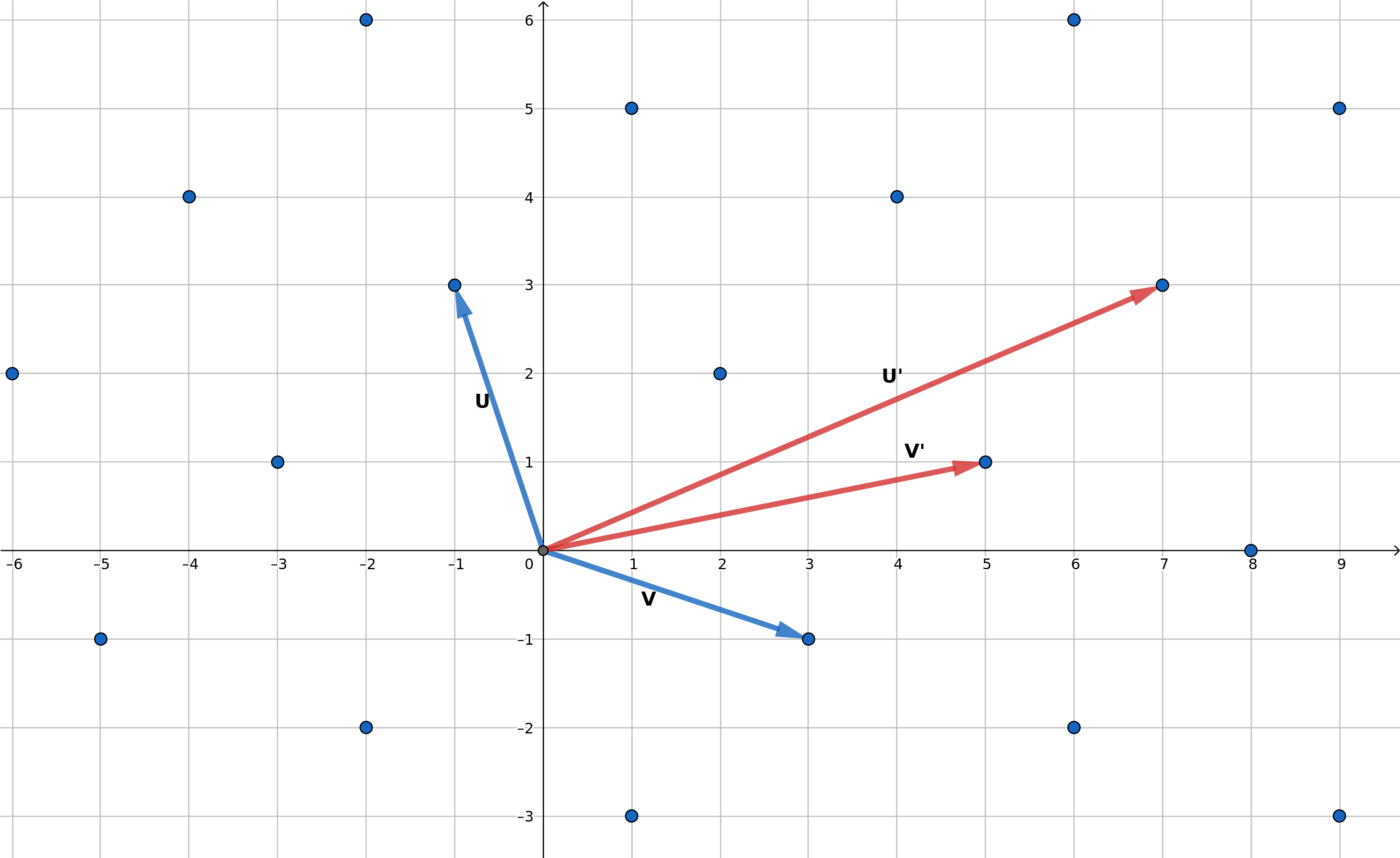
Un réseau euclidien peut être représenté par plusieurs bases (image ci-contre).Dans un réseau euclidien, différemment du système de coordonnées du plan (0,x,y), les coordonnées sont toujours des entiers et la base n'est pas nécessairement rectangulaire.
Bonne ou mauvaise base ?
Certaines bases vont être plus qualitatives que d'autres. Une bonne base (base bleue) est presque rectangulaire alors qu'une mauvaise base (base rouge) est de forme quelconque.
Dans notre exemple, nous avons donc deux bases. Une bonne base représentée par les vecteurs u et v, et une mauvaise base représentée par les vecteurs u' et v'.
Bonne base :
Mauvaise base :
Qu'est ce que ces typologies changent ? Pour expliquer cela, on peut évoquer l'utilisation des réseaux euclidiens dans les modems : on souhaite transmettre des messages numériques entre deux machines. Cependant la transmission est analogique donc du bruit peut altérer le message. Si un point du réseau représente le message à l'envoi, on a un vecteur d'erreur ou vecteur bruit appliqué sur ce point à la réception. Comme représenté sur les images ci-dessous, plus la base est bonne, plus la zone autour de chaque point couvrira au mieux l'espace, et plus simple sera la correction du message. Cela est à condition que l'erreur ne soit pas trop grande. Si la base est mauvaise l'erreur sera alors vite trop grande.
En cryptologie, nous allons nous baser sur ces typologies pour les mêmes raisons (voir Algorithme de Babai).
Application en cryptologie
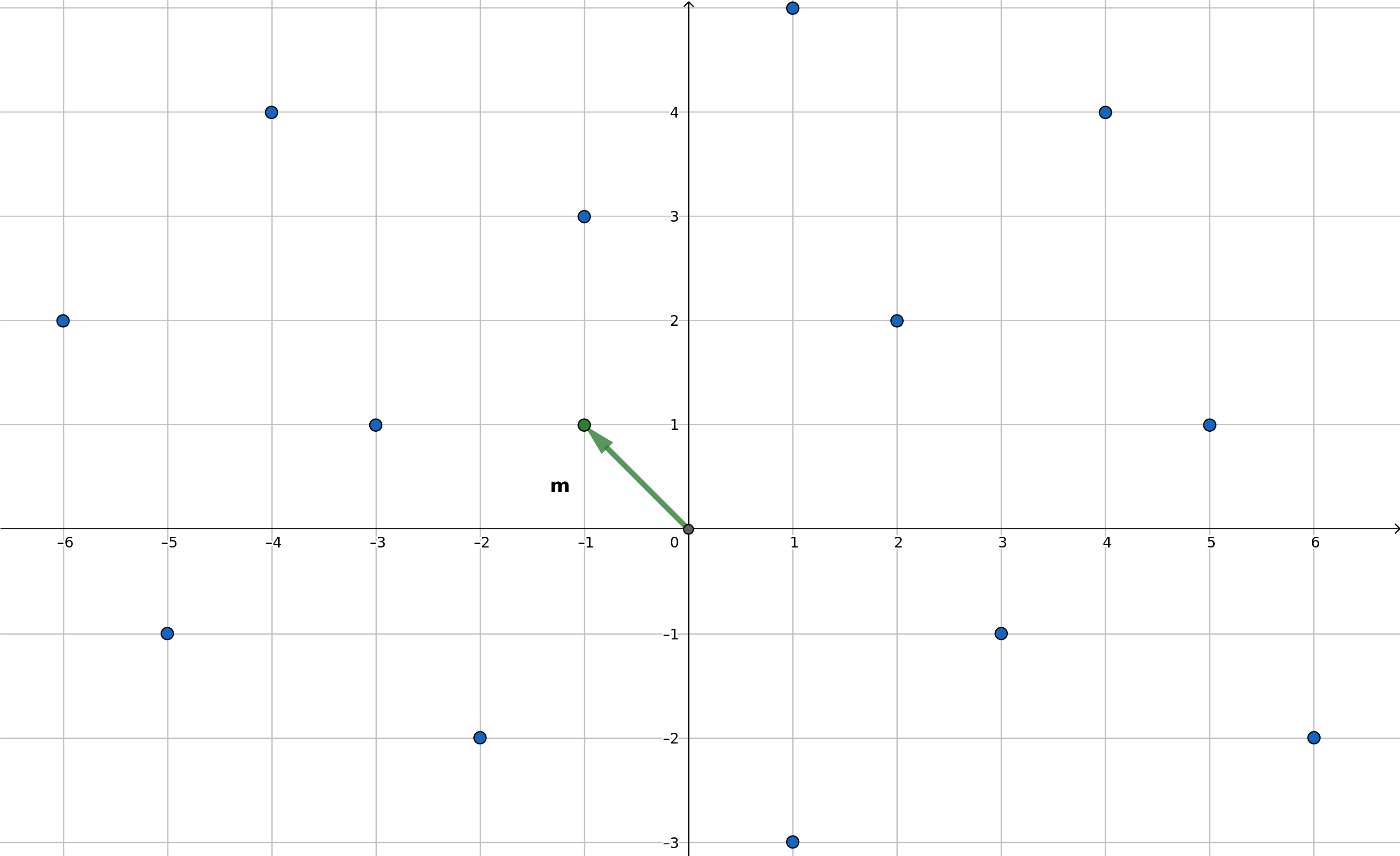
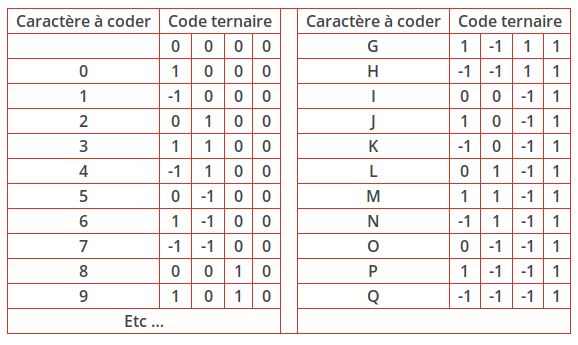
Nous allons utiliser une bonne base comme clé privée et une mauvaise base comme clé publique. Pour représenter un message sur le réseau euclidien, il suffit de coder notre message en ternaire, les valeurs possibles sont 0,1,-1. Il est important de savoir que le nombre de digits d'un message représentera le nombre de dimensions du réseau euclidien. Plus le message est long, plus la difficulté sera élevée. Dans une dimension 8, le message OK correspondra donc à m = 0 -1 -1 1 -1 0 -1 1. Si on revient en dimension 2, le message ternaire m = -1 1 est représenté par un vecteur m = .
Le chiffrement
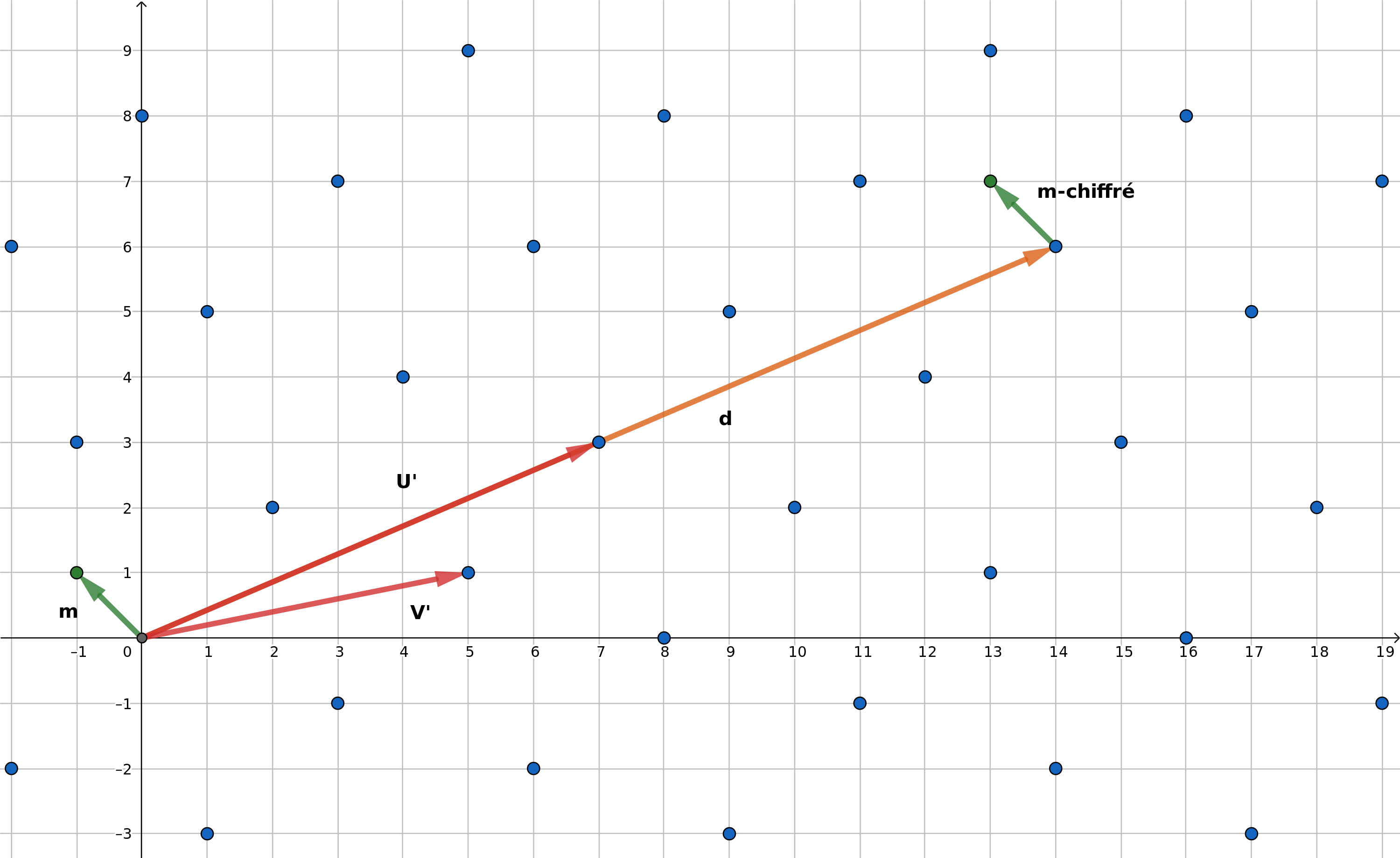
Pour le chiffrement nous utilisons notre clé publique (mauvaise base) pour tirer un point aléatoire sur le réseau. Ensuite on addition notre vecteur message m avec le vecteur d, qui correspond à notre point tiré au hasard.
def chiffre(Pub, m): d = tirage_reseau(Pub) m_chiffré = d + m return m_chiffré
Dans notre exemple, on obtient alors un nouveau vecteur correspondant au message chiffré :
Message chiffré :
.
Le déchiffrement
Pour le déchiffrement, il suffit de retrouver le point représenté par le vecteur d grâce à notre clé privée. Pour cela on utilise l'algorithme de Babai qui va paver l'espace avec au centre de chaque pavé un point du réseau. Et ensuite permettre de retrouver le point du pavé (le point du réseau représenté par le vecteur d) où se trouve notre vecteur message chiffré. Un fois le vecteur d retrouvé on le soustrait au vecteur message chiffré.
def dechiffre(Secret, m_chiffré): d = Algorithme_de_Babai(Secret, m_chiffré) m = m_chiffré - d return m
Algorithme de Babai
C'est un mathématicien du nom de László Babai qui a inventé la meilleure solution pour retrouver le centre du pavé associé au message chiffré :
Algorithme_de_Babai(B, m_chiffré){
B_inv = inverse(B)
v = m_chiffré * B_inv
w = vector([round(x) for x in v])
d = B * w
return d
}
L'algorithme marche ainsi :
On renseigne la base sous forme de matrice où chaque colonne représente un vecteur de dimension. Cette base sera plus ou moins bonne en fonction de la clé (privée ou publique).
On renseigne le message chiffré également sous forme de matrice à une colonne.
Bonne base (clé privée) :
Message chiffré :
Ensuite il s'agit de calculer l'inverse de la matrice B en appliquant la formule classique :
Formule :
Résultat :
Il faut alors effectuer une multiplication matricielle avec B_inv et le message chiffré m_chiffre que l'on va arrondir ensuite:
Opération :
*
Résultat arrondi :
Enfin, on ré-effectue une multiplication matricielle avec B et notre résultat w:
Opération :
*
Vecteur d:
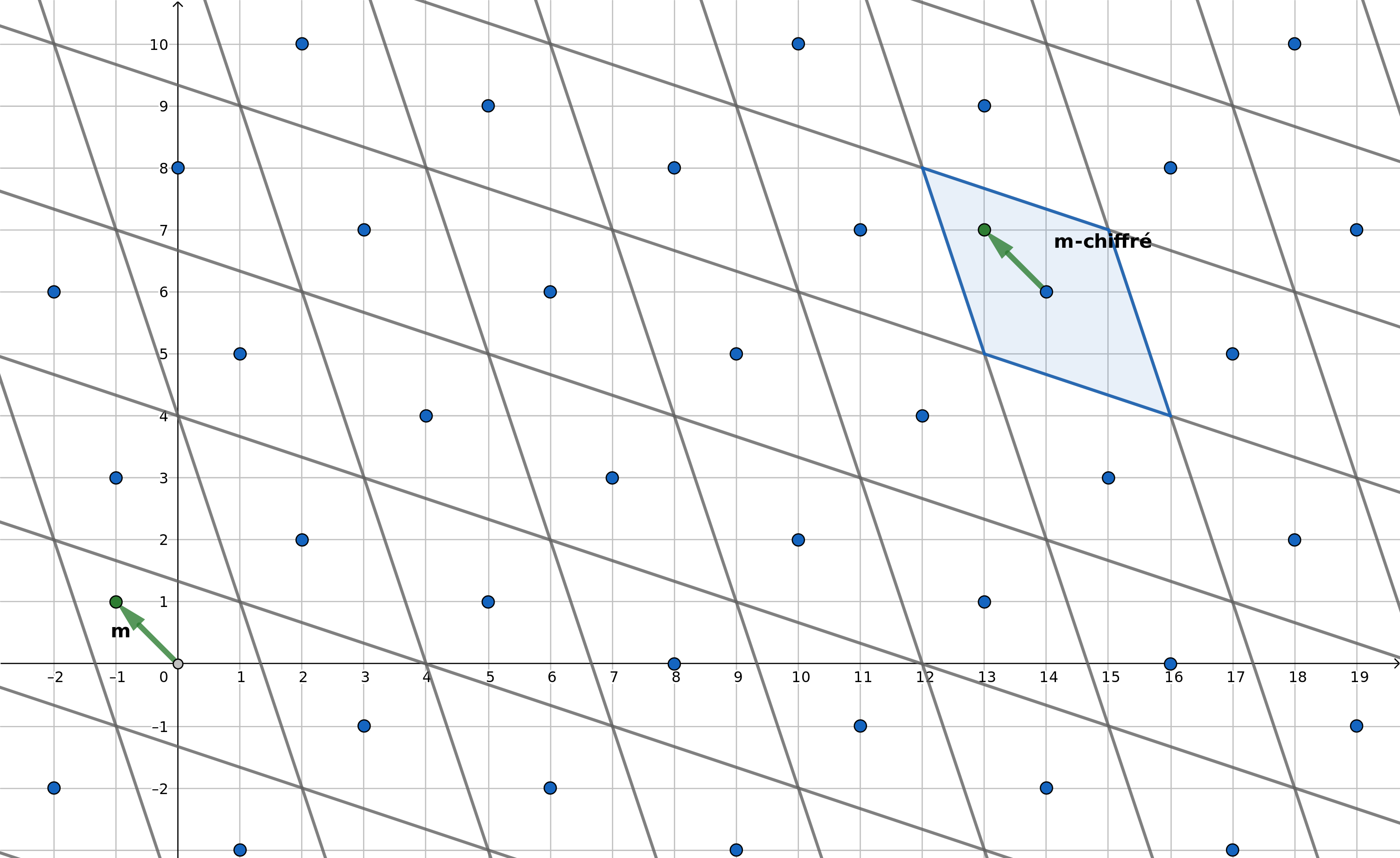
On obtient donc le vecteur d que l'on avait ajouté au message clair lors du chiffrement. (Voir première image ci-contre)
Si on utilise la clé publique comme paramètre de cette algorithme, On ne trouvera pas le bon pavé et donc on ne trouvera pas le bon vecteur d. (Voir la deuxième photo ci-contre)
On retrouve donc la même problématique que dans l'exemple sur les modems plus haut.
Robustesse
La cryptologie sur les réseaux euclidiens est basé sur des problèmes NP-complets. Ce sont des problèmes impossible à résoudre pour les calculateurs classiques ou quantiques de manière efficace. De plus, se baser sur des problèmes NP-Complets est d'autant plus intéressant puisqu'il est sûr et certain qu'aucun algorithme quantique ne pourra en venir à bout de manière efficace. En effet, on sait que les algorithmes quantiques sont limités à la classe BQP et résoudre ce type de problème ne permet pas de résoudre les problèmes NP-complets.
Il y a plusieurs problèmes algorithmiques dans les réseaux :
- SVP (Shortest Vector Problem) qui permet de trouver le plus court vecteur non nul, c’est un algorithme NP-difficile.
- CVP (Closest Vector Problem) qui permet de trouver le vecteur le plus proche d’un vecteur donné dans un réseau. Il est également NP-difficile.
- La réduction de réseau, il s’agit de trouver une bonne base d’un réseau euclidien.
Pour réduire un réseau euclidien de dimension 2, il existe une méthode simple et efficace très similaire à l'algorithme d'Euclide pour calculer le PGCD de deux entiers. Comme avec l'algorithme euclidien, la méthode est itérative, à chaque étape, le plus grand des deux vecteurs est réduit en ajoutant ou en soustrayant un multiple entier du plus petit vecteur.
Cependant le temps croît de manière exponentielle quand le nombre de dimensions augmente. A partir de 80 dimensions, un effort considérable est déjà requis. Les records sur clusters atteignent avec difficultés, 130 dimensions. On considère qu'avec 200 ou 250 dimensions les réseaux euclidiens sont assez robustes puisque l'on estime le temps de calculs en milliards d'années.
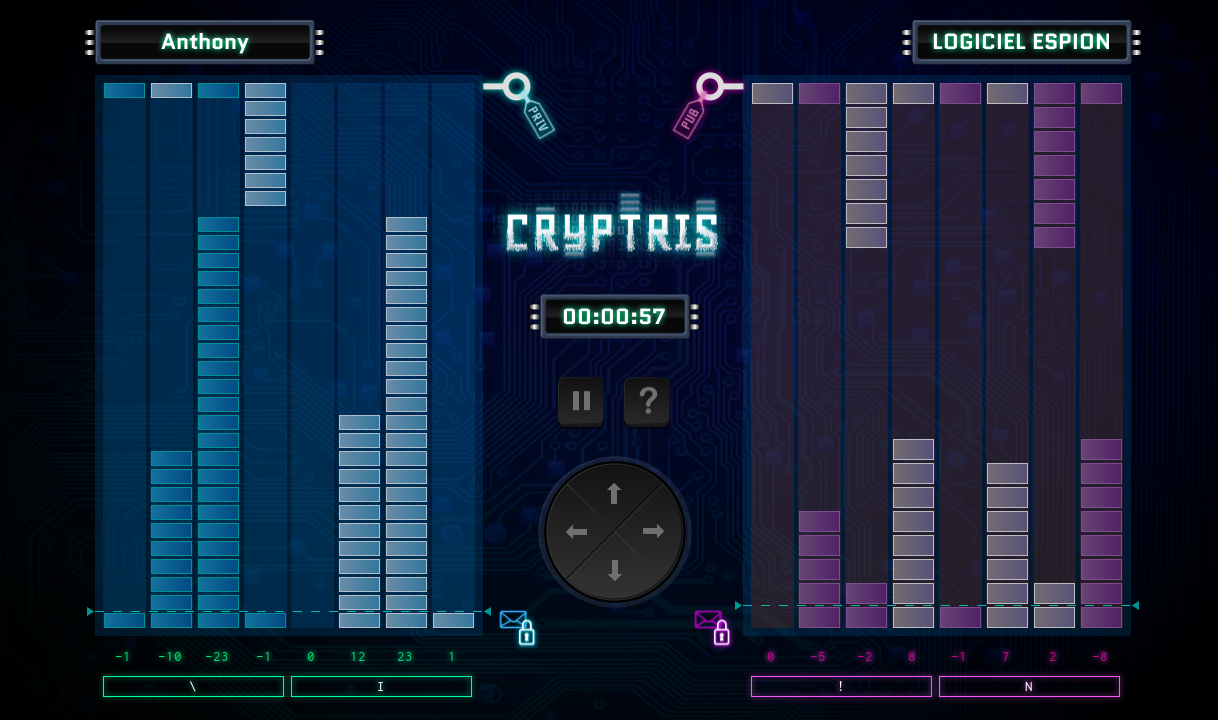
Un jeu sur les reseaux euclidiens : Cryptris
Cryptris est un jeu basé sur les réseaux euclidiens, il a été conçu en collaboration avec l'INRIA, et réalisé par Digitalcuisine. Le jeu est open source, et fonctionne entièrement en HTML5. Ce jeu permet d'illustrer les notions que nous avons pu voir plus haut de manière plus ludique. Deux articles de vulgarisations scientifiques sont disponibles et expliquent les notions misent en oeuvre dans le jeu pour ainsi mieux comprendre cette méthode cryptographique.
Chiffrement homomorphe
Le chiffrement homomorphe permet d'effectuer une ou plusieurs opérations sans la nécessité d'accéder aux données sensibles en les déchiffrant.
Pour toutes opérations Op et pour tous messages m1 et m2, effectuer l'opération sur les messages cryptés par la méthode C et ensuite déchiffés par D est équivalent au résultat de l'opération sur les deux messages clairs :
Prenons l'exemple d'Alice. Alice souhaite pouvoir effectuer des opérations sur deux données sensibles mais elle ne possède pas la puissance de calcul nécessaire pour l'effectuer. Elle souhaite donc demander à un organisme tiers de procéder aux calculs sur ses données. Cependant, les données à traiter sont sensibles et Alice ne fait pas confiance en cet organisme. Elle va donc utiliser un chiffrement homomorphe et envoyer des données chiffrées à l'organisme qui pourra ainsi calculer et renvoyer le résultat, encore chiffré, à Alice. Alice pourra alors déchiffrer le message pour obtenir le résultat de l'opération sur ses données sensibles grâce aux propriétés du chiffrement homomorphe.
Chiffrement homomorphe et Cryptographie
Le chiffrement RSA, actuellement très utilisé, est considéré comme partiellement homomorphe. En effet, le chiffrement permet d'effectuer certaines opérations de manière homomorphe mais n'offre pas la possibilité d'effectuer l'ensemble des opérations existantes. Plus particulièrement, ce genre de chiffrement autorise soit la multiplication homomorphe soit l'addition homomorphe :
Multiplication homomorphe :
En revanche, le chiffrement par réseaux euclidiens est dit complètement homomorphe et permet donc d'effectuer l'ensemble des opérations de manière homomorphe. Pour qu'un chiffrement soit complètement homomorphe, il faut pouvoir appliquer les opérations d'addition et de multiplication sur les données chiffrées :
Multiplication homomorphe :
Addition homomorphe :
On peut voir le XOR comme une addition modulo 2 et la propriété logique AND comme la multiplication modulo 2. Grace à ces deux portes logiques, il est possible d'exprimer tous les programmes et calculs existant. L'ensemble de ces deux opérations permettrait alors de pouvoir effectuer l'ensemble des opérations existantes et d’accéder à un homomorphisme complet.
C'est pourquoi le chiffrement par réseaux euclidiens est d'autant plus intéressant pour l'avenir de la cyber-sécurité.
Conclusion
Bien que ce type de chiffrement soit prometteur pour l'avenir, certains points noirs peuvent être cités.
En effet, alors que la taille des clés de chiffrement de la méthode RSA se situe entre 128 à 512 octets, celle des clés du cryptage par réseaux euclidiens représente plusieurs méga-octets et reste donc beaucoup trop lourde aujourd'hui pour être viable.
De plus, il faut savoir que l'addition et la multiplication homomorphe sont 1000 fois plus longues que les opérations classiques.
Ces deux inconvénients, bien qu'ils paraissent insignifiant, constituent aujourd'hui le problème majeur du chiffrement. De nombreux chercheurs dont Craig Gentry, le premier à avoir écrit une thèse sur cette méthode de chiffrement en 2009, travaille sur la réduction de la taille des clés ainsi que sur la performance pour effectuer les opérations homomorphes.
Bibliographie
Réseaux euclidiens
Article de vulgarisation Cryptris 1
Article de vulgarisation Cryptris 2
La menace des ordinateurs quantiques
Les 5 innovations qui changeront nos vies mes 5 prochaines années
5 innovations à venir
linuxfr - Le chiffrement homomorphe
Mathématique - Chiffrement homomorphe
Réduction des réseaux euclidiens
Problèmes algorithmiques sur les réseaux euclidiens