« Apprentissage automatique » : différence entre les versions
Aucun résumé des modifications |
|||
| (53 versions intermédiaires par 2 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
L'objectif de ce projet était de se familiariser et de comprendre l'apprentissage automatique, plus communément appelé Deep Learning. Pour ceci, il faut premièrement définir ce qu'est un neurone (en informatique) et |
L'objectif de ce projet était de se familiariser et de comprendre l'apprentissage automatique, plus communément appelé Deep Learning. Pour ceci, il faut premièrement définir ce qu'est un neurone (en informatique) et par la suite un réseau de neurones. On parlera ensuite de la façon dont ces systèmes s'adaptent d'eux même, et comment optimiser leur vitesse pour obtenir un réseau performant. |
||
== Deep Learning == |
== Deep Learning == |
||
Le Deep Learning est le procédé par lequel un programme va apprendre lui même tout au long de son fonctionnement, mais plus particulièrement durant une période |
Le Deep Learning est le procédé par lequel un programme va apprendre lui même tout au long de son fonctionnement, mais plus particulièrement durant une période appelée le "training", l'entraînement en français. Durant cette période, on donne au programme des échantillons d'entraînement, qui contiennent la réponse que devrait donner le programme pour que celui-ci s'adapte en fonction de ses erreurs. À la fin, le programme possède un pourcentage de réussite qui définit sa fiabilité par la suite. |
||
== Neurones == |
== Neurones == |
||
Pour |
Pour qu'un apprentissage ait lieu il faut un support qui peut supporter des changements. Ces supports sont des neurones: |
||
=== Perceptrons === |
=== Perceptrons === |
||
[[Fichier:Perceptron.png]]<br/> |
[[Fichier:Perceptron.png]]<br/> |
||
Ce type de neurone créé dans les années 50 a un fonctionnement simple. En effet, le neurone prend plusieurs entrées |
Ce type de neurone créé dans les années 50 a un fonctionnement simple. En effet, le neurone prend plusieurs entrées binaires (0 ou 1) pour donner une sortie binaire. |
||
<br/>[[Fichier:Percerptron_eq.png]]<br/> |
<br/>[[Fichier:Percerptron_eq.png]]<br/> |
||
Comme le |
Comme le montrent les inéquations ci dessus, chaque entrée possède un poids qui donne son importance. Si la somme du produit de chaque entrée et de son poids est supérieur à une valeur seuil alors le neurone donne un 1 sinon il donne un 0. |
||
Nous pouvons aussi interpréter ces inéquations, en faisant entrer en jeu le biais noté b qui va être en quelque sorte la difficulté pour que le perceptron retourne un 1. |
Nous pouvons aussi interpréter ces inéquations, en faisant entrer en jeu le biais noté b qui va être en quelque sorte la difficulté pour que le perceptron retourne un 1. |
||
<br/> |
<br/> |
||
[[Fichier:Perceptron_eq_biais.png]] |
[[Fichier:Perceptron_eq_biais.png]] |
||
<br/> |
<br/> |
||
Pour améliorer le jugement d'un perceptron, il faut donc faire varier le poids et le biais de chaque entrée afin de retourner le bit qu'il doit donner. |
Pour améliorer le jugement d'un perceptron, il faut donc faire varier le poids et le biais de chaque entrée afin de retourner le bit qu'il doit donner. |
||
=== Les neurones sigmoïdes === |
=== Les neurones sigmoïdes === |
||
Un majeur problème du perceptron est qu'un faible changement des poids et des biais |
Un majeur problème du perceptron est qu'un faible changement des poids et des biais peut entraîner un changement total du résultat, nous éloignant fortement du résultat attendu. Nous voulons qu'un petit changement nous rapproche encore plus du résultat parfait, quoi qu'il arrive pour éviter les erreurs, et ne nous mène pas vers un résultat complètement différent.<br/> |
||
Le neurone sigmoïde est fait pour éviter |
Le neurone sigmoïde est fait pour éviter ces problèmes, en effet, comme le perceptron, il possède un poids et un biais par entrée; cependant sa sortie n'est pas 0 ou 1 mais σ(w⋅x+b) où |
||
<br/> |
<br/> |
||
[[Fichier:Sigmoid_function.png]] |
[[Fichier:Sigmoid_function.png]] |
||
<br/> |
<br/> |
||
Si z est positif et très grand alors σ(z) est environ égal à 1, si z est négatif et très petit alors σ(z) est environ |
Si z est positif et très grand alors σ(z) est environ égal à 1, si z est négatif et très petit alors σ(z) est environ égal à 0. Dans les extrêmes le neurone sigmoïde se comporte tout comme un perceptron. La différence est visible quand w⋅x+b est un nombre de taille raisonnable, la sortie n'étant plus 0 ou 1 mais un flottant compris entre 0 et 1. On peut voir cela sur la courbe de la fonction : |
||
<br/> |
<br/> |
||
[[Fichier:Coubre_sigmoid.png]] |
[[Fichier:Coubre_sigmoid.png]] |
||
<br/> |
<br/> |
||
Le neurone sigmoïde est donc bien plus précis que le perceptron évitant les dérivations du résultat. |
Le neurone sigmoïde est donc bien plus précis que le perceptron évitant les dérivations du résultat. <br/><br/> |
||
=== Réseaux de neurones === |
=== Réseaux de neurones === |
||
L'objectif |
L'objectif d'un neurone n'est pas de rester seul mais de former un réseau, les sorties de plusieurs neurones devenant les entrées d'un neurone. |
||
<br/> |
<br/> |
||
[[Fichier:Reseau.png]] |
[[Fichier:Reseau.png]] |
||
| Ligne 39 : | Ligne 39 : | ||
-les couches cachées <br/> |
-les couches cachées <br/> |
||
-la couche de sorties <br/> <br/> |
-la couche de sorties <br/> <br/> |
||
Comme |
Comme son nom l'indique, la couche d'entrées contient les entrées données au programme qui vont ensuite être envoyées aux différents neurones de la couche suivante. Cette entrée peut être les bits de l'objet à traiter, un par neurone. La couche de sorties contient tous les neurones qui vont donner le résultat du réseau, il peut très bien y en avoir un ou plusieurs. <br/> |
||
Par exemple: <br/> |
Par exemple: <br/> |
||
[[Fichier:Reseau_sortie.png]] <br/> |
[[Fichier:Reseau_sortie.png]] <br/> |
||
Ou encore: <br/> |
Ou encore: <br/> |
||
[[Fichier:Reseau_sorties.png]] <br/> <br/> |
[[Fichier:Reseau_sorties.png]] <br/> <br/> |
||
== Descente de gradient == |
|||
Afin de trouver les bons poids et biais pour qu'un neurone fonctionne sans problème, il faut savoir de combien les modifier. On appelle ce procédé la descente de gradient. On prend une fonction que l'on appelle fonction de coût dont les variables sont le poids et le biais, cette fonction représente la distance entre le résultat obtenu et le résultat que nous aurions dû obtenir. L'objectif est de minimiser la fonction en trouvant les poids et biais correspondants. |
|||
<br/> |
|||
[[Fichier:graph_cost.png]] |
|||
<br/> |
|||
On comprend grâce à cet exemple de graphique de fonction de coût qu'en trouvant les valeurs de poids et biais adéquats (ici matérialisés par v1,v2,etc en fonction du nombre de dimension), on obtient le minimum de la fonction et donc on en conclut que les poids et biais sont les bons. <br/> |
|||
D'où le terme de descente de gradient, on cherche à descendre la pente de la fonction pour trouver les bonnes valeurs. |
|||
<br/> |
|||
[[Fichier:Grad_form.png]] |
|||
<br/> |
|||
Cela nous donne cette équation, cela nous montre bien, qu'un changement dans les poids et les biais mène à un changement de la valeur de la fonction de coût. |
|||
Cette forme donne donc naissance à une autre forme généralisée à toutes les dimensions: |
|||
<br/> |
|||
[[Fichier:form_gen_grad1.png]] |
|||
où |
|||
[[Fichier:form_gen_grad2.png]] |
|||
et |
|||
[[Fichier:form_gen_grad3.png]] |
|||
<br/> |
|||
Dans l'équation Δv, on note la présence de η qui est le taux d'apprentissage, il permet de choisir à quel point on veut évoluer vite, cependant si la valeur de η est trop grande ou trop petite cela peut nuire à la rapidité d'apprentissage. |
|||
=== Backpropagation === |
|||
Cependant pour que la fonction de coût ait un impact sur tout le réseau, il faut pouvoir le parcourir à nouveau pour modifier les valeurs comme il se doit en fonction de l'erreur. La fonction de coût fonctionne avec les résultats. <br/> <br/> |
|||
Pour cela on utilise la backpropagation, qui comme son nom l'indique, consiste, en partant du résultat, à trouver les erreurs sur chaque poids ou biais grâce aux couches précédentes. <br/> <br/> |
|||
En propageant l'erreur vers l'arrière, on peut bien voir quels poids ont causé la plus grande divergence sur le neurone suivant permettant de les mettre à jour. Par la méthode de la descente de gradient on obtient alors des poids plus près de ceux voulus. On répète ensuite cet algorithme pour chaque échantillon d'entraînement pour obtenir un réseau correct. |
|||
== Application == |
|||
Nous allons maintenant créer un réseau que l'on va entraîner à reconnaître des chiffres manuscrits. <br/> |
|||
Pour cela nous allons utiliser plusieurs librairies dont la plus importante : PyTorch, faite pour le deep learning et qui possède un tutoriel très pratique pour se familiariser, elle facilitera l'implémentation des réseaux, fonction de coût et la backpropagation.<br/> |
|||
On utilise ici la base de données MNIST contenant 60000 échantillons d'entraînement et 10000 de test. <br/> |
|||
Le code final se trouve dans la partie source. <br/><br/> |
|||
=== Préliminaires === |
|||
Il faut premièrement importer tout ce dont nous aurons besoin: |
|||
<br/> |
|||
<br/> |
|||
[[Fichier:import.png]] |
|||
<br/> |
|||
<br/> |
|||
Ensuite, on importe les données pour l'entraînement et les tests. <br/> |
|||
On définit aussi le nombre de canaux pour les couleurs en transformant les images en tensor (type de matrice utilisée ici) et en les normalisant. |
|||
<br/> |
|||
On définit les classes possibles, nos résultats. |
|||
<br/> |
|||
<br/> |
|||
[[Fichier:Data_import.png]] |
|||
<br/> |
|||
=== Réseau === |
|||
Nous allons maintenant créer le réseau: <br/><br/> |
|||
[[Fichier:class.png]] |
|||
<br/><br/> |
|||
Pour ceci on définit de multiples fonctions, qui vont définir le réseau. <br/> |
|||
On définit le nombre de canal de couleurs, ici 1, la définition de l'image et le réseau et ses dimensions avec <code> nn.Linear </code> avec lequel on définit le nombre de valeurs d'entrée et de sortie. Cette fonction va appliquer la transformation linéaire y = x*W^T + b avec x l'entrée ,y la sortie et w et b respectivement les poids et biais. <br/> |
|||
On définit ensuite la fonction forward qui va permettre d'évoluer dans le réseau. |
|||
<br/> |
|||
=== Entraînement === |
|||
On doit maintenant définir la phase d'entraînement:<br/> <br/> |
|||
[[Fichier:training.png]] |
|||
<br/><br/> |
|||
Nous avons premièrement besoin de définir la fonction de coût (ici loss) et la méthode de descente de gradient (ici SGD = Stochastic Gradient Descent).<br/> |
|||
Nous allons faire 2 époques d'entraînement, ce qui est largement suffisant dans notre cas. <br/> |
|||
Par la suite on prend des échantillons et leur classe et on les fait passer dans le réseau. Ensuite on calcule l'erreur, on la renvoie dans le réseau à l'aide de <code>.backward()</code> et on actualise les poids et biais à l'aide de <code>optimizer.step()</code> <br/> |
|||
Pour voir l'avancement du processus on ajoute un affichage nous montrant l'époque, le nombre d'échantillons déjà utilisés et l'erreur moyenne des 2000 derniers échantillons. <br/> |
|||
Pour finir cette phase d'entraînement, on sauvegarde l'état actuel du réseau.<br/> |
|||
=== Test === |
|||
Nous devons maintenant tester la fiabilité du réseau, pour cela on charge des images aléatoires, on les passe dans le réseau et on compare les résultats. <br/><br/> |
|||
[[Fichier:Test_res.png]] |
|||
<br/> |
|||
=== Additionnel === |
|||
Comme vu dans le paragraphe précédent, on affiche l'image à l'aide de la fonction <code> imshow </code>. Celle-ci transforme les images pour être affichées grâce à matplotlib:<br/><br/> |
|||
[[Fichier:Imshow.png]] <br/><br/> |
|||
Nous avons aussi deux fonctions qui affichent les pourcentages de réussite globale sur les 10000 échantillons de test et de chaque chiffre. <br/><br/> |
|||
[[Fichier:accuracy.png]]<br/><br/> |
|||
Ces deux fonctions testent sur 10000 échantillons, cependant avec l'attribut <code> .no_grad() </code> le réseau s'exécute sans calculer les gradients, les erreurs ou encore la backprop, rendant le processus plus rapide car nous voulons juste les résultats. <br/> |
|||
=== Résultats === |
|||
J'ai dit précédemment que seulement 2 époques de test allaient nous suffire, en effet si on regarde les résultats obtenus on peut voir que l'on a une précision de 98% ce qui est déjà très correct pour une utilisation comme la nôtre.<br/> |
|||
Dans le milieu professionnel comme la lecture de chèque de banque 2% d'erreur ne seraient pas acceptables.<br/><br/> |
|||
[[Fichier:Precision.png]] |
|||
== Sources == |
|||
[https://github.com/Kroklethon/VISI201/blob/master/reconnaissance_chiffre.py CODE ENTIER]<br/> |
|||
[http://www.http://neuralnetworksanddeeplearning.com/ Neural Networks and Deep Learning] <br/> |
|||
[https://pytorch.org/ PyTorch]<br/> |
|||
[https://www.miximum.fr/blog/introduction-au-deep-learning-2/ Backpropagation]<br/> |
|||
Dernière version du 19 mai 2020 à 08:22
L'objectif de ce projet était de se familiariser et de comprendre l'apprentissage automatique, plus communément appelé Deep Learning. Pour ceci, il faut premièrement définir ce qu'est un neurone (en informatique) et par la suite un réseau de neurones. On parlera ensuite de la façon dont ces systèmes s'adaptent d'eux même, et comment optimiser leur vitesse pour obtenir un réseau performant.
Deep Learning
Le Deep Learning est le procédé par lequel un programme va apprendre lui même tout au long de son fonctionnement, mais plus particulièrement durant une période appelée le "training", l'entraînement en français. Durant cette période, on donne au programme des échantillons d'entraînement, qui contiennent la réponse que devrait donner le programme pour que celui-ci s'adapte en fonction de ses erreurs. À la fin, le programme possède un pourcentage de réussite qui définit sa fiabilité par la suite.
Neurones
Pour qu'un apprentissage ait lieu il faut un support qui peut supporter des changements. Ces supports sont des neurones:
Perceptrons
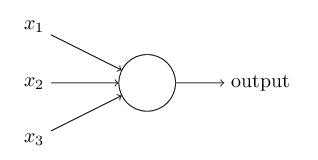
Ce type de neurone créé dans les années 50 a un fonctionnement simple. En effet, le neurone prend plusieurs entrées binaires (0 ou 1) pour donner une sortie binaire.
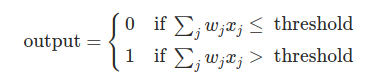
Comme le montrent les inéquations ci dessus, chaque entrée possède un poids qui donne son importance. Si la somme du produit de chaque entrée et de son poids est supérieur à une valeur seuil alors le neurone donne un 1 sinon il donne un 0.
Nous pouvons aussi interpréter ces inéquations, en faisant entrer en jeu le biais noté b qui va être en quelque sorte la difficulté pour que le perceptron retourne un 1.
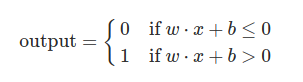
Pour améliorer le jugement d'un perceptron, il faut donc faire varier le poids et le biais de chaque entrée afin de retourner le bit qu'il doit donner.
Les neurones sigmoïdes
Un majeur problème du perceptron est qu'un faible changement des poids et des biais peut entraîner un changement total du résultat, nous éloignant fortement du résultat attendu. Nous voulons qu'un petit changement nous rapproche encore plus du résultat parfait, quoi qu'il arrive pour éviter les erreurs, et ne nous mène pas vers un résultat complètement différent.
Le neurone sigmoïde est fait pour éviter ces problèmes, en effet, comme le perceptron, il possède un poids et un biais par entrée; cependant sa sortie n'est pas 0 ou 1 mais σ(w⋅x+b) où
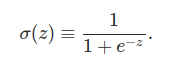
Si z est positif et très grand alors σ(z) est environ égal à 1, si z est négatif et très petit alors σ(z) est environ égal à 0. Dans les extrêmes le neurone sigmoïde se comporte tout comme un perceptron. La différence est visible quand w⋅x+b est un nombre de taille raisonnable, la sortie n'étant plus 0 ou 1 mais un flottant compris entre 0 et 1. On peut voir cela sur la courbe de la fonction :
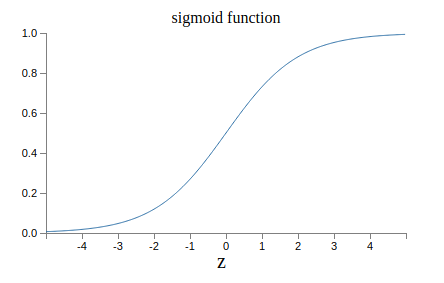
Le neurone sigmoïde est donc bien plus précis que le perceptron évitant les dérivations du résultat.
Réseaux de neurones
L'objectif d'un neurone n'est pas de rester seul mais de former un réseau, les sorties de plusieurs neurones devenant les entrées d'un neurone.
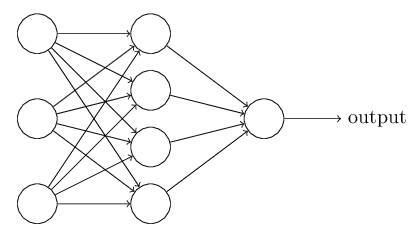
Ces réseaux sont constitués de différentes couches:
-la couche d'entrées
-les couches cachées
-la couche de sorties
Comme son nom l'indique, la couche d'entrées contient les entrées données au programme qui vont ensuite être envoyées aux différents neurones de la couche suivante. Cette entrée peut être les bits de l'objet à traiter, un par neurone. La couche de sorties contient tous les neurones qui vont donner le résultat du réseau, il peut très bien y en avoir un ou plusieurs.
Par exemple:
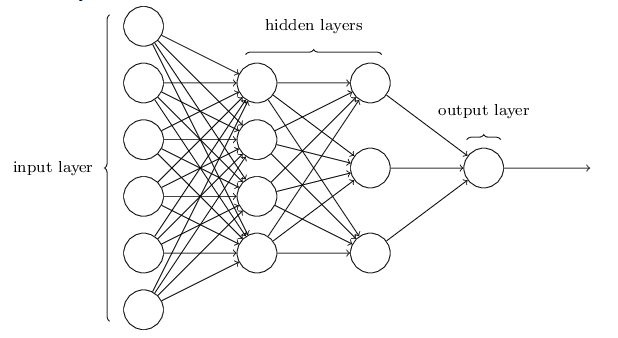
Ou encore:
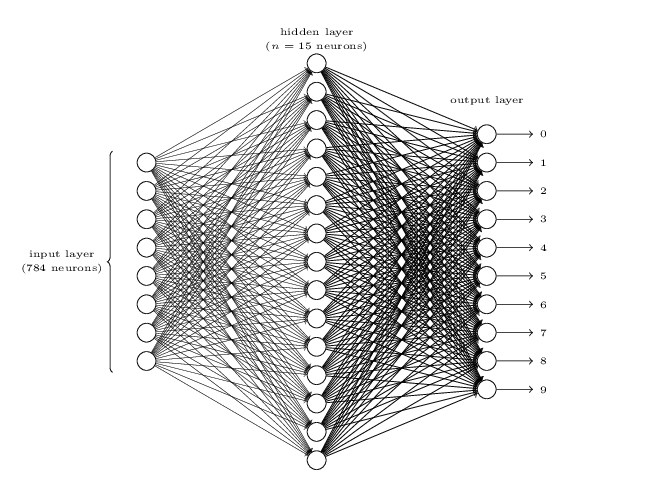
Descente de gradient
Afin de trouver les bons poids et biais pour qu'un neurone fonctionne sans problème, il faut savoir de combien les modifier. On appelle ce procédé la descente de gradient. On prend une fonction que l'on appelle fonction de coût dont les variables sont le poids et le biais, cette fonction représente la distance entre le résultat obtenu et le résultat que nous aurions dû obtenir. L'objectif est de minimiser la fonction en trouvant les poids et biais correspondants.
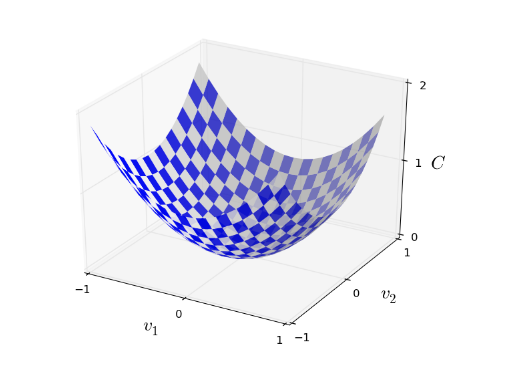
On comprend grâce à cet exemple de graphique de fonction de coût qu'en trouvant les valeurs de poids et biais adéquats (ici matérialisés par v1,v2,etc en fonction du nombre de dimension), on obtient le minimum de la fonction et donc on en conclut que les poids et biais sont les bons.
D'où le terme de descente de gradient, on cherche à descendre la pente de la fonction pour trouver les bonnes valeurs.
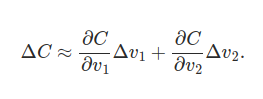
Cela nous donne cette équation, cela nous montre bien, qu'un changement dans les poids et les biais mène à un changement de la valeur de la fonction de coût.
Cette forme donne donc naissance à une autre forme généralisée à toutes les dimensions:
![]() où
où
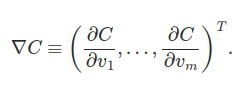 et
et
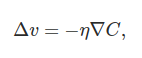
Dans l'équation Δv, on note la présence de η qui est le taux d'apprentissage, il permet de choisir à quel point on veut évoluer vite, cependant si la valeur de η est trop grande ou trop petite cela peut nuire à la rapidité d'apprentissage.
Backpropagation
Cependant pour que la fonction de coût ait un impact sur tout le réseau, il faut pouvoir le parcourir à nouveau pour modifier les valeurs comme il se doit en fonction de l'erreur. La fonction de coût fonctionne avec les résultats.
Pour cela on utilise la backpropagation, qui comme son nom l'indique, consiste, en partant du résultat, à trouver les erreurs sur chaque poids ou biais grâce aux couches précédentes.
En propageant l'erreur vers l'arrière, on peut bien voir quels poids ont causé la plus grande divergence sur le neurone suivant permettant de les mettre à jour. Par la méthode de la descente de gradient on obtient alors des poids plus près de ceux voulus. On répète ensuite cet algorithme pour chaque échantillon d'entraînement pour obtenir un réseau correct.
Application
Nous allons maintenant créer un réseau que l'on va entraîner à reconnaître des chiffres manuscrits.
Pour cela nous allons utiliser plusieurs librairies dont la plus importante : PyTorch, faite pour le deep learning et qui possède un tutoriel très pratique pour se familiariser, elle facilitera l'implémentation des réseaux, fonction de coût et la backpropagation.
On utilise ici la base de données MNIST contenant 60000 échantillons d'entraînement et 10000 de test.
Le code final se trouve dans la partie source.
Préliminaires
Il faut premièrement importer tout ce dont nous aurons besoin:
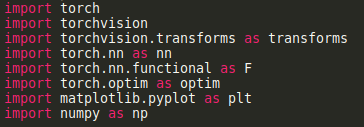
Ensuite, on importe les données pour l'entraînement et les tests.
On définit aussi le nombre de canaux pour les couleurs en transformant les images en tensor (type de matrice utilisée ici) et en les normalisant.
On définit les classes possibles, nos résultats.
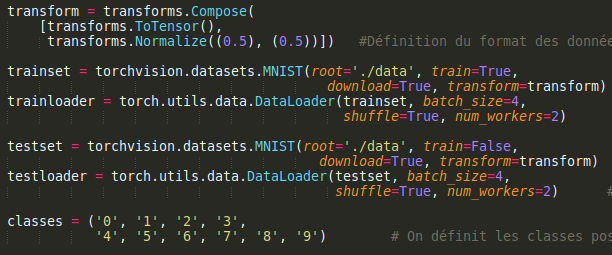
Réseau
Nous allons maintenant créer le réseau:
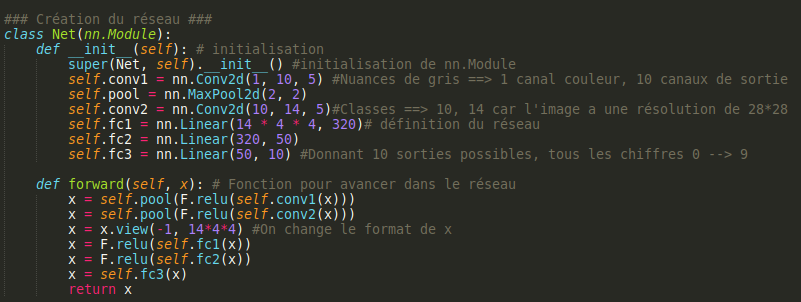
Pour ceci on définit de multiples fonctions, qui vont définir le réseau.
On définit le nombre de canal de couleurs, ici 1, la définition de l'image et le réseau et ses dimensions avec nn.Linear avec lequel on définit le nombre de valeurs d'entrée et de sortie. Cette fonction va appliquer la transformation linéaire y = x*W^T + b avec x l'entrée ,y la sortie et w et b respectivement les poids et biais.
On définit ensuite la fonction forward qui va permettre d'évoluer dans le réseau.
Entraînement
On doit maintenant définir la phase d'entraînement:
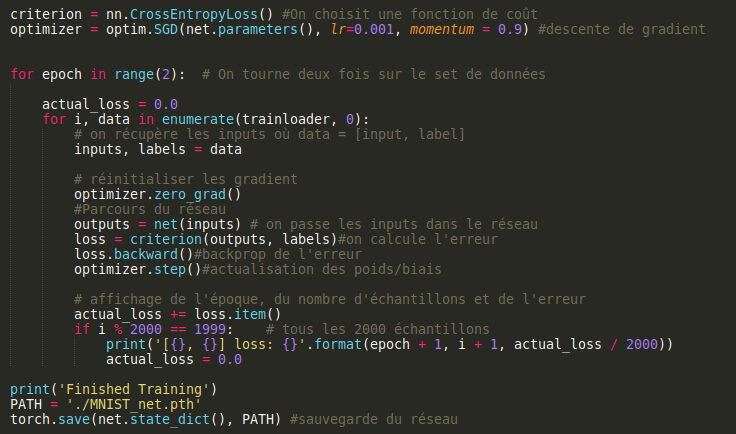
Nous avons premièrement besoin de définir la fonction de coût (ici loss) et la méthode de descente de gradient (ici SGD = Stochastic Gradient Descent).
Nous allons faire 2 époques d'entraînement, ce qui est largement suffisant dans notre cas.
Par la suite on prend des échantillons et leur classe et on les fait passer dans le réseau. Ensuite on calcule l'erreur, on la renvoie dans le réseau à l'aide de .backward() et on actualise les poids et biais à l'aide de optimizer.step()
Pour voir l'avancement du processus on ajoute un affichage nous montrant l'époque, le nombre d'échantillons déjà utilisés et l'erreur moyenne des 2000 derniers échantillons.
Pour finir cette phase d'entraînement, on sauvegarde l'état actuel du réseau.
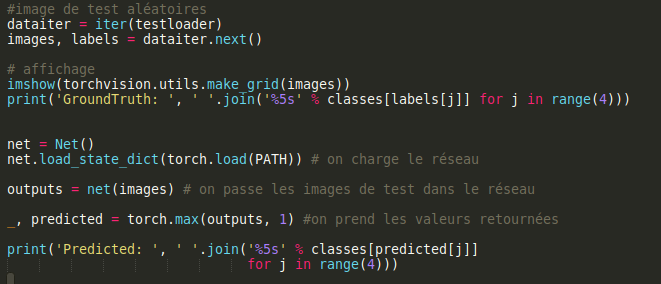
Test
Nous devons maintenant tester la fiabilité du réseau, pour cela on charge des images aléatoires, on les passe dans le réseau et on compare les résultats.
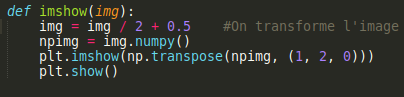
Additionnel
Comme vu dans le paragraphe précédent, on affiche l'image à l'aide de la fonction imshow . Celle-ci transforme les images pour être affichées grâce à matplotlib:
Nous avons aussi deux fonctions qui affichent les pourcentages de réussite globale sur les 10000 échantillons de test et de chaque chiffre.
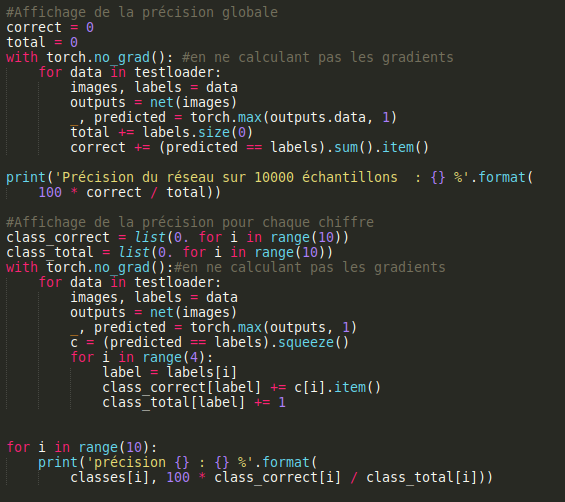
Ces deux fonctions testent sur 10000 échantillons, cependant avec l'attribut .no_grad() le réseau s'exécute sans calculer les gradients, les erreurs ou encore la backprop, rendant le processus plus rapide car nous voulons juste les résultats.
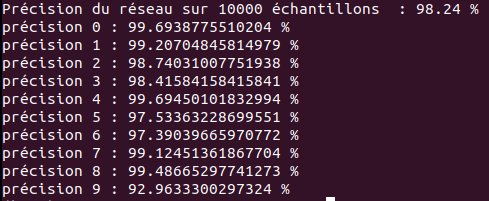
Résultats
J'ai dit précédemment que seulement 2 époques de test allaient nous suffire, en effet si on regarde les résultats obtenus on peut voir que l'on a une précision de 98% ce qui est déjà très correct pour une utilisation comme la nôtre.
Dans le milieu professionnel comme la lecture de chèque de banque 2% d'erreur ne seraient pas acceptables.
Sources
CODE ENTIER
Neural Networks and Deep Learning
PyTorch
Backpropagation