« Structures de données purement fonctionnelles » : différence entre les versions
Aucun résumé des modifications |
Aucun résumé des modifications |
||
| (13 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 249 : | Ligne 249 : | ||
=== Tas gaucher === |
=== Tas gaucher === |
||
[[Fichier:Schema_2.png|150px|thumb|right|Exemple de tas gaucher et illustration de la notion de rang.]] |
|||
Un tas est une version d'arbre particulière. En effet, elle se caractérise par le fait que la valeur de chaque nœud ne peut être plus grand que n'importe laquelle de ses enfants. Cette caractéristique fait que l'élément le plus petit se trouve toujours à la racine. |
|||
Un tas est dit gaucher si le rang de n'importe quel enfant de gauche est supérieur ou égal à celui de l'enfant de droit qui lui est associé. On appelle rang d'un nœud la longueur de sa ''colonne vertébrale droite'', c'est-à-dire le chemin le plus à droite qui va de ce nœud à une feuille. Une conséquence simple de cette propriété est que la colonne vertébrale droite d'un nœud constitue le chemin le plus court de ce nœud à une feuille. |
|||
Soit r le rang de la racine d'un tas gaucher de taille n. On peut en déduire que chaque nœud de profondeur inférieure ou égale à r-1 a exactement deux enfants, car sinon r aurait une valeur plus faible ou la propriété gauchère ne serait pas respectée. Ainsi, on peut affirmer que la taille d'un tas est donc d'au moins 2<sup>r</sup> - 1. De ce fait, on peut en déduire que le rang de la racine vaut au plus log(n + 1). Par conséquent, la colonne vertébrale droite d'un tas gaucher de taille n comporte au plus ⌊log(n + 1)⌋ éléments. |
|||
''Code de la structure tas gaucher'' |
|||
<pre lang="OCaml">module LeftistHeap (O: ORDERED) = struct |
|||
type elem = O.t |
|||
type heap = Nil | Cons of (int * heap * elem * heap) |
|||
let rank = fun h -> |
|||
match h with |
|||
| Nil -> 0 |
|||
| Cons(r, _, _, _) -> r |
|||
let makeH... |
|||
let merge... |
|||
let insert... |
|||
exception EmptyHeap |
|||
let findMin... |
|||
let deleteMin... |
|||
end;;</pre> |
|||
Ici, nous allons étudier les fonctions merge, insert, findMin et deleteMin. |
|||
* '''merge - Fusionne deux tas''' |
|||
Afin de simplifier l'opération, on remarque que la colonne vertébrale droite d'un tas gaucher est ordonnée. On en déduit que le concept clé est de fusionner les colonnes vertébrales des deux tas comme on fusionnerait deux listes triées avant d'échanger les enfants le long de la branche afin de restaurer la propriété gauchère. |
|||
Comme il a été démontré précédemment que la longueur de la colonne vertébrale est au plus logarithmique, on peut en déduire que merge a un temps d'exécution d'ordre O(log n). |
|||
<pre lang="OCaml">let makeH = fun v a b -> |
|||
if rank a >= rank b |
|||
then Cons(rank b + 1, a, v, b) |
|||
else Cons(rank a + 1, b, v, a) |
|||
let rec merge = fun x y -> |
|||
match x, y with |
|||
| Nil, _ -> y |
|||
| _, Nil -> x |
|||
| Cons(_, e11, v1, e12), Cons(_, e21, v2, e22) -> if (O.leq v1 v2) |
|||
then makeH v1 e11 (merge e12 y) |
|||
else makeH v2 e21 (merge x e22)</pre> |
|||
Ici, on fait appel à une fonction intermédiaire : makeH. |
|||
Cette fonction compare le rang des deux tas et échange les enfants si besoin afin de respecter la propriété gauchère. |
|||
Ensuite, concernant merge en elle-même, on compare les valeurs des deux racines et on fait appel à makeH pour combiner et potentiellement échanger les enfants. |
|||
* '''insert - Insère une valeur dans l'arbre''' |
|||
Une fois merge défini, il suffit d'établir que l'on veut fusionner le tas avec un tas d'une seule valeur. Et puisque le temps d'exécution de merge est d'ordre O(log n), il en va de même pour insert. |
|||
<pre lang="OCaml">let insert = fun v h -> (merge (Cons(1, Nil, v, Nil)) h)</pre> |
|||
* '''findMin - Récupère le minimum''' |
|||
Comme le minimum est par définition à la racine, le temps d'exécution de findMin est d'ordre O(1), donc constant. |
|||
<pre lang="OCaml">let findMin = fun h -> |
|||
match h with |
|||
| Nil -> raise EmptyHeap |
|||
| Cons(_, _, v, _) -> v</pre> |
|||
* '''deleteMin - Supprime le minimum''' |
|||
Similairement, le minimum étant à la racine, on peut établir que le supprimer revient à fusionner ses enfants. De plus, merge ayant un temps d'exécution d'ordre O(log n), celui de deleteMin est le même. |
|||
<pre lang="OCaml">let deleteMin = fun h -> |
|||
match h with |
|||
| Nil -> raise EmptyHeap |
|||
| Cons(_, a, _, b) -> merge a b</pre> |
|||
=== Tas binomial === |
=== Tas binomial === |
||
[[File:Schema_3.png|300px|thumb|right|Représentation des arbres binaires de rangs 0 à 3]] |
|||
Les tas binomiaux sont des tas composés d'un type plus primitif appelé arbre binomial. Les arbres binomiaux sont défini inductivement comme suit : |
|||
* Un arbre binomial de rang 0 est un singleton de nœud ; |
|||
* Un arbre binomial de rang r est formé en liant deux arbres binomiaux de rang r-1 tel qu'un des arbres devient l'enfant le plus à gauche de l'autre. |
|||
De cette définition, on comprend qu'un arbre binomial de rang r contient exactement 2<sup>r</sup> nœuds. |
|||
Il existe une deuxième définition équivalente des arbres binomiaux : |
|||
* Un arbre binomial de rang r est un nœud ayant r enfants t<sub>1</sub> à t<sub>r</sub> où chaque enfant t<sub>i</sub> est un arbre binomial de rang r - i. |
|||
Dans le code ci-dessous, on représente un nœud dans un arbre binomial comme un élément avec une liste de ses enfants. Par commodité, on note aussi le rang de chaque nœud. |
|||
De plus, un tas binomial étant une liste d'arbres binomiaux ne pouvant comporter qu'un seul arbre d'un rang donné et un arbre binomial de rang r comportant 2<sup>r</sup> éléments, on constate alors que les arbres d'un tas binomial de taille n correspondent à la représentation binaire de n. |
|||
Par exemple, la représentation binaire de 13 est 1101, donc un tas binomial de taille 13 contient un arbre de rang 0, un de rang 2 et un de rang 3 (de taille respective 1, 4 et 8). |
|||
De plus, comme la représentation binaire de n contient au plus ⌊log(n + 1)⌋ bits à 1, un tas binomial de taille n contient au plus ⌊log(n + 1)⌋ arbres. |
|||
<pre lang="OCaml">module BinomialHeap (O: ORDERED) = struct |
|||
type elem = O.t |
|||
type tree = Node of (int * elem * tree list) |
|||
type heap = tree list |
|||
exception EmptyHeap |
|||
let rank (Node(r, _, _)) = r |
|||
let root (Node(_, x, _)) = x |
|||
let link = ... |
|||
let rec insTree... |
|||
let insert = ... |
|||
let rec merge... |
|||
let rec removeMinTree... |
|||
let findMin = ... |
|||
let deleteMin = ... |
|||
end;;</pre> |
|||
Les fonctions que nous allons étudier ici sont link, insert, merge, findMin et deleteMin. |
|||
* '''link - Lie deux arbres de même rang pour en construire un de rang supérieur''' |
|||
Les arbres étant triés en respectant la propriété du tas, il suffit de comparer les racines pour voir lequel reste au sommet en les liant, l'autre étant ajouté à la liste des enfants. |
|||
<pre lang="OCaml">let link = fun (Node(r, x1, c1) as t1) (Node(_, x2, c2) as t2) -> |
|||
if (O.leq x1 x2) |
|||
then Node(r + 1, x1, t2 :: c1) |
|||
else Node(r + 1, x2, t1 :: c2)</pre> |
|||
* '''insert - Insertion d'un élément''' |
|||
Les fonctions insert et merge sont toutes deux vaguement comparables à l'addition de deux nombres binaires. Pour insérer un nouvel élément, on crée un singleton d'arbre (donc de rang 0) puis on parcourt tous les arbres du tas par ordre croissant de rang jusqu'à trouver un rang manquant en liant les arbres de rang égal en chemin. On peut comparer le lien à une retenue arithmétique. |
|||
<pre lang="OCaml">let rec insTree = fun t ls -> |
|||
match ls with |
|||
| [] -> [t] |
|||
| t' :: ts' as ts -> if rank t < rank t' |
|||
then t :: ts |
|||
else insTree (link t t') ts' |
|||
let insert = fun x ts -> insTree (Node(0, x, [])) ts</pre> |
|||
Le pire scénario étant dans un tas de taille n = 2<sup>k</sup> - 1 qui nécessiterait k liens, donnant un temps d'exécution d'ordre O(log n). |
|||
* '''merge - Fusion de deux tas''' |
|||
Comme précédemment, merge parcourt la liste d'arbres de chaque tas par ordre croissant de rang en liant les arbres de rang égal. |
|||
<pre lang="OCaml">let rec merge = fun ts1 ts2 -> |
|||
match ts1, ts2 with |
|||
| _, [] -> ts1 |
|||
| [], _ -> ts2 |
|||
| t1 :: ts1', t2 :: ts2' -> if rank t1 < rank t2 |
|||
then t1 :: (merge ts1' ts2) |
|||
else if rank t2 < rank t1 |
|||
then t2 :: (merge ts1 ts2') |
|||
else insTree (link t1 t2) (merge ts1' ts2')</pre> |
|||
* '''findMin et deleteMin - Trouve et supprime le minimum respectivement''' |
|||
Ces deux fonctions ont besoin de la même fonction auxiliaire, à savoir removeMinTree, qui trouve l'arbre avec la plus petite valeur et l'extrait de la liste, retournant à la fois l'arbre et le reste de la liste. |
|||
<pre lang="OCaml">let rec removeMinTree = fun ls -> |
|||
match ls with |
|||
| [] -> raise EmptyHeap |
|||
| [t] -> (t, []) |
|||
| t :: ts -> let (t', ts') = removeMinTree ts in |
|||
if (O.leq (root t) (root t')) |
|||
then (t, ts) |
|||
else (t', t :: ts') |
|||
let findMin = fun ts -> let (t, _) = removeMinTree ts in root t |
|||
let deleteMin = fun ts -> let (Node(_, x, ts1), ts2) = removeMinTree ts in merge (rev ts1) ts2</pre> |
|||
À partir de là, findMin retourne juste la racine de l'arbre. Cependant, deleteMin est plus complexe. En effet, après avoir retiré la racine de l'arbre, il faut remettre la liste d'enfants de l'arbre avec le reste de la liste des arbres. Cela dit, bien que chaque liste d'enfants est une collection d'arbres binomiaux de rang unique, ceux-ci sont triés ''par ordre décroissant de rang et non par ordre croissant''. Afin de convertir cette liste en tas binomial valide, on l'inverse à l'aide de la fonction rev avant de la fusionner avec les arbres restants. |
|||
=== Arbre rouge / noir === |
=== Arbre rouge / noir === |
||
[[File:Schema_4.png|300px|thumb|right|Illustration des invariants]] |
|||
Précédemment, nous avons vu les arbres de recherche binaires. Bien que cette structure fonctionne bien avec des données aléatoires ou désordonnées, leur performance est grandement réduite avec des données ordonnées car toutes les opérations ont un temps d'exécution d'ordre allant jusqu'à O(n). Une solution à ce problème est de garder chaque arbre relativement équilibré. Ainsi, aucune opération n'a de temps d'exécution d'ordre excédant O(log n). Une famille d'arbres de recherche binaires équilibrés populaire est celle des '''arbres bicolores, ou arbres rouge-noir'''. |
|||
Un arbre bicolore est un arbre binaire dont chaque nœud a une couleur, rouge ou noir. On considère qu'un nœud vide est noir. |
|||
De plus, un arbre bicolore doit respecter deux invariants : |
|||
# '''Aucun nœud rouge ne peut avoir d'enfant rouge.''' |
|||
# '''Toutes les branches allant de la racine à une feuille doivent avoir le même nombre de nœuds noirs.''' |
|||
De ces deux invariants, on peut extraire que le chemin le plus long - alternant nœuds noirs et rouge - est au plus deux fois plus long que le chemin le plus court - composé uniquement de nœuds noirs. |
|||
En reprenant la démonstration faite sur la longueur de la colonne vertébrale d'un tas gaucher, on sait que le chemin le plus court d'un arbre de profondeur n contient au plus ⌊log(n + 1)⌋ éléments. Par conséquent, on peut en déduire que le chemin le plus long contient au plus 2⌊log(n + 1)⌋ éléments. |
|||
<pre lang="OCaml">module RedBlackTree(O: ORDERED)= struct |
|||
type elem = O.t |
|||
type color = R | B |
|||
type tree = E | T of (color * tree * elem * tree) |
|||
let balance... |
|||
let rec member = fun x t -> |
|||
match t with |
|||
| E -> false |
|||
| T(_, e1, y, e2) -> if (O.lt x y) |
|||
then member x a |
|||
else if (O.lt y x) |
|||
then member x b |
|||
else true |
|||
let rec insert... |
|||
end;;</pre> |
|||
Ici, nous allons étudier les fonctions insert et balance. Mis à part le caractère générique pour la couleur, member fonctionne comme pour les arbres binaires non équilibrés. |
|||
* '''insert - Insertion d'une nouvelle valeur dans l'arbre''' |
|||
La différence majeure entre cette fonction et sa variante pour les arbres non équilibrés relève du respect des invariants. |
|||
<pre lang="OCaml">let insert = fun x t -> |
|||
let fun ins = function E -> T(R, E, x, E) |
|||
| T(color, e1, y, e2) as t' -> if (O.lt x y) |
|||
then balance (color, ins a, y, b) |
|||
else if (O.lt y x) |
|||
then balance (color, a, y, ins b) |
|||
else t' |
|||
in let T(_, e1, y, e2) = ins t |
|||
in T(B, e1, y, e2)</pre> |
|||
Cette fonction étend la variante non équilibrée sur trois axes majeurs : |
|||
Premièrement, quand on crée un nouveau nœud, on le colore initialement en rouge. Deuxièmement, on force le nœud final à être noir, indépendamment de la couleur retournée par la fonction ins. Enfin, on replace les appels au constructeur T par des appels à la fonction balance, chargée de construire un nœud tout en modifiant l'arbre pour respecter les invariants d'équilibre. |
|||
* '''balance - Équilibrage de l'arbre selon les invariants''' |
|||
En donnant la couleur rouge à un nouveau nœud, on maintient l'invariant 2 mais viole l'invariant 1 à chaque fois que le parent est rouge. Pour ce faire, on autorise une violation rouge-rouge à la fois que l'on fait remonter le long de la branche de recherche vers la racine en équilibrant. |
|||
La fonction balance détecte une violation rouge-rouge quand il voit une suite noir-rouge-rouge et la corrige (voir figure ci-dessous). |
|||
[[File:Schema_5.png|none|500px|thumb|left|Fonctionnement de la fonction balance]] |
|||
Ici, le code essaie de trouver l'un des quatre cas noir-rouge-rouge ne respectant pas l'invariant 1, puis de le corriger. Si aucun cas n'est trouvé, alors on construit le sous-arbre tel quel. |
|||
<pre lang="OCaml">let balance = function |
|||
(B,T (R,T (R,a,x,b),y,c),z,d) -> T (R,T (B,a,x,b),y,T (B,c,z,d)) |
|||
| (B,T (R,a,x,T (R,b,y,c)),z,d) -> T (R,T (B,a,x,b),y,T (B,c,z,d)) |
|||
| (B,a,x,T (R,T (R,b,y,c),z,d)) -> T (R,T (B,a,x,b),y,T (B,c,z,d)) |
|||
| (B,a,x,T (R,b,y,T(R,c,z,d))) -> T (R,T (B,a,x,b),y,T (B,c,z,d)) |
|||
| (c,a,x,b) -> T (c,a,x,b)</pre> |
|||
== Évolution du domaine de recherche == |
== Évolution du domaine de recherche == |
||
Après s'être penché en détail sur la thèse d'Okasaki, voici quelques articles plus récents en rapport avec le sujet permettant d'élargir la question. |
|||
* '''Manufacturing Datatypes''' par Ralf Hinze, publié en 1999 et édité par Okasaki traitant d'une structure générale pour construire des structures de données purement fonctionnelles permettant de satisfaire des contraintes de taille ou de forme, notamment pour l'implémentation de matrices et de certains types d'arbres. |
|||
* '''Scrap your boilerplate: a practical design pattern for generic programming''' de Ralf Lämmel et Simon Peyton-Jones proposant un modèle de métastructure, c'est-à-dire (une structure permettant de générer du code ?), afin de remédier à l'usage de code passe-partout, autrement dit du code répété à plusieurs reprises avec très peu de modifications. |
|||
* '''Finger trees: a simple general-purpose data structure''' de Ralf Hinze et Ross Paterson introduisant une nouvelle structure : les arbres pointés 2-3 permettant d'accéder aux feuilles dans un laps de temps amorti constant. Cette structure peut servir de base pour plusieurs autres structures de données. |
|||
* '''Parallel Concurrent ML''' de John Reppy, Claudio V. Russo et Yingqi Xiao présentant le langage fonctionnel concurrent CML (pour Concurrent ML), c'est-à-dire que le programme peut utiliser plusieurs processus simultanément, réduisant le temps d'exécution. |
|||
== Sources et annexes == |
== Sources et annexes == |
||
| Ligne 265 : | Ligne 528 : | ||
* [https://doc.lagout.org/programmation/Functional%20Programming/Chris_Okasaki-Purely_Functional_Data_Structures-Cambridge_University_Press%281998%29.pdf Purely functional data structures, Chris Okasaki] |
* [https://doc.lagout.org/programmation/Functional%20Programming/Chris_Okasaki-Purely_Functional_Data_Structures-Cambridge_University_Press%281998%29.pdf Purely functional data structures, Chris Okasaki] |
||
* [https://fr.wikipedia.org/wiki/Programmation_fonctionnelle Programmation fonctionnelle (Wikipédia)] |
* [https://fr.wikipedia.org/wiki/Programmation_fonctionnelle Programmation fonctionnelle (Wikipédia FR)] |
||
* [https://en.wikipedia.org/wiki/Leftist_tree Tas gaucher (Wikipédia EN)] |
|||
'''Annexes''' |
'''Annexes''' |
||
* [http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.39.5334&rep=rep1&type=pdf#page=7 Manufacturing Datatypes] |
|||
* [https://www.researchgate.net/publication/221282345_Scrap_Your_Boilerplate_A_Practical_Design_Pattern_for_Generic_Programming Scrap your boilerplate: a practical design pattern for generic programming] |
|||
* [https://archive.alvb.in/msc/03_infoafp/papers/2012-12-18_WerkCollege_FingerTreesRalfHinze.pdf Finger trees: a simple general-purpose data structure] |
|||
* [https://www.microsoft.com/en-us/research/wp-content/uploads/2009/09/Parallel-Concurrent-ML.pdf Parallel Concurrent ML] |
|||
Dernière version du 29 mai 2020 à 09:02
Présentation du problème
Lorsque l'on souhaite coder une structure de données dans un langage impératif comme C, Ada, Pascal ou Perl, il est très facile de trouver des livres sur le sujet. En revanche, si l'on souhaite utiliser le paradigme fonctionnel, que ce soit Lisp, Haskell ou OCaml, le choix est nettement plus restreint.
Un programmeur peut choisir le paradigme de son langage, pourvu que ce soit impératif.
- Chris Okasaki, pastiche d'une citation de Ford, Purely functional data structures, 1996
Ainsi, Chris Okasaki a voulu explorer à travers sa thèse (et son livre la développant) diverses structures de données adaptées au paradigme fonctionnel.
Mais avant d'étudier les solutions proposées, il est nécessaire de définir quelques contraintes et termes.
Problèmes liés au paradigme fonctionnel
Le paradigme fonctionnel est principalement basé sur l'évaluation de fonctions et d'expressions mathématiques, et tout ce qui ne peut être représenté ainsi n'est pas admis.
De ce fait naît le premier obstacle à la création de structures de données purement fonctionnelles : Le changement d'état étant banni, on ne peut pas réaliser d'assignation de variable.
Là où les langages impératifs font fréquemment usage de l'assignation de variable et de la modification de valeurs, il faut trouver d'autres solutions en fonctionnel pour contourner ce problème. Okasaki compare le lien entre l'assignation et le programmeur à celui entre les couteaux et un chef cuisinier. Dans les deux cas, un mauvais usage peut être dangereux et destructeur, mais extrêmement efficace avec un usage intelligent.
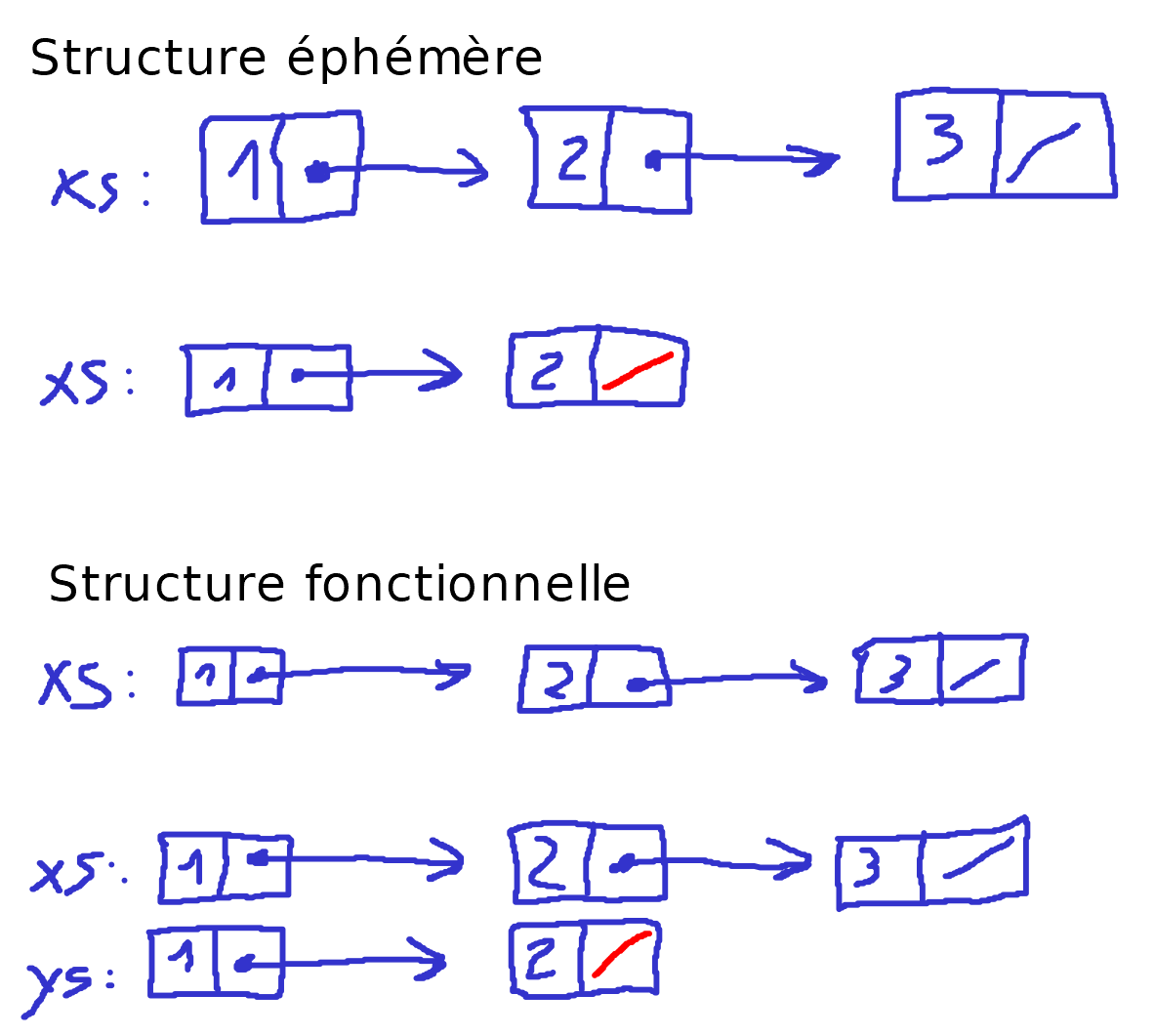
Une deuxième difficulté liée à l'absence d'assignation provient du fait que l'on attende davantage une persistance d'une structure de données fonctionnelle. En effet, là où il est admis que l'actualisation d'une structure impérative détruit l'ancienne version pour ne garder que la nouvelle (ce genre de structure de données est dit "éphémère"), on s'attend que l'actualisation d'une structure fonctionnelle donne l'accès aux deux versions (d'où la notion de structure "persistante"). Il est possible d'avoir des structures persistantes en impératif, mais on associera ici la notion d'éphémérité au paradigme impératif tandis que la persistance sera liée au paradigme fonctionnel.
Enfin, un troisième problème lié au paradigme fonctionnel relève du temps d'exécution, le fonctionnel étant généralement considéré comme étant moins efficace que l'impératif. Ainsi, il est nécessaire de trouver des structures de données qui soient aussi efficaces que celles utilisées en impératif.
Évaluation stricte et évaluation paresseuse
On appelle évaluation stricte une technique d'implémentation d'un programme récursif où les arguments sont évalués avant le corps de la fonction. L'évaluation est dite paresseuse quand les arguments sont évalués lors du premier appel par la fonction avant d'être mis en cache pour un autre usage ultérieur.
Chaque type d'évaluation a ses avantages et inconvénients. Une évaluation stricte permettra de gérer le cas "Pire scénario" tandis qu'une évaluation paresseuse sera plus à l'aise avec les structures dites amorties.
Un avantage indéniable qu'a cependant l'évaluation stricte sur l'évaluation paresseuse est que l'on peut calculer le temps d'évaluation plus facilement (notion de comparaison asymptotique, notamment du grand O de Landau).
Vocabulaire
Avant de commencer à étudier les solutions proposées par Okasaki, il est nécessaire de poser quelques termes de vocabulaire.
- Abstraction
- Un type de données abstrait, autrement dit un type et un ensemble de fonctions agissant sur ce type.
Exemple : Le premier bloc de code de liste chaînée (voir ci-dessous) est une abstraction de cette structure, avec le type élément et les divers constructeurs, destructeurs et méthodes sur cette structure.
- Implémentation
- Une réalisation concrète d'une abstraction. Il est important de noter qu'une implémentation ne correspond pas nécessairement à du code, un modèle concret suffit.
Exemple : Posons qu'un élément est soit null, soit le couplet liant un entier et un pointeur vers l'élément suivant. Ceci correspond à l'implémentation de l'abstraction de la structure liste chaînée.
- Objet / Version
- Une instance d'un type de données, telle une variante spécifique de liste ou d'arbre.
Exemple : Soit une liste chaînée d'entiers. Il s'agit d'une version d'une liste chaînée.
- Identité persistante
- Une identité unique et invariante malgré les changements. Par exemple, "la pile" en parlant de toutes ses différentes versions correspond à son identité persistante.
Maintenant que nous avons posé des bases solides, nous pouvons commencer à étudier les diverses structures de données proposées par Okasaki. Le langage utilisé est OCaml.
Solutions proposées
En se basant sur la présentation, on peut faire remarquer deux points :
- Afin d'avoir des structures persistantes, il est nécessaire de travailler sur une copie de l'argument plutôt que l'argument lui-même
- À l'exception de la liste chaînée, toutes les structures évoquées ci-après ne fonctionnent qu'avec des types ordonnés.
module type ORDERED = sig
type t
val eq: t -> t -> bool
val lt: t -> t -> bool
val leq: t -> t -> bool
end;;
Code permettant d'implémenter un type polymorphe ordonné. On admet que ce type est défini pour toutes les structures ci-dessous.
Liste chaînée
Cette structure basique sert d'introduction à la persistance, ce qui nous permet de présenter les différences d'implémentation de cette structure dans un paradigme impératif comparé à un paradigme fonctionnel.
Abstraction de la structure liste chaînée
module type LIST = sig
type 'a t
(* Constructeurs *)
val nil: 'a t
val cons: 'a -> 'a t -> 'a t
val is_empty: 'a t -> bool
(* Destructeurs *)
val head: 'a t -> 'a
val tail: 'a t -> 'a t
(* Méthodes *)
val append: 'a t -> 'a t -> 'a t
val update: 'a t -> int -> 'a -> 'a t
val suffixes: 'a t -> 'a t t
end;;
Ici, nous allons observer les méthodes, à savoir append, update et suffixes.
- append - Concaténation de deux listes
Soient xs et ys deux listes et zs la concaténation de xs et ys.
En impératif, une structure de données efficace basée sur la liste chaînée peut comporter deux pointeurs globaux, un sur le premier élément et un sur le dernier. Ainsi, pour concaténer xs et ys, il suffit de modifier le dernier élément de xs pour qu'il pointe vers le premier de ys. L'avantage, c'est que le temps d'exécution est d'ordre O(1), donc constant. Cependant, en obtenant zs, on garde ys mais on perd xs.
En fonctionnel, zs est une reconstruction de xs à laquelle on accole ys. Si on note n la longueur de xs, la fonction a un temps d'exécution d'ordre O(n), mais on garde toujours xs et ys.
let rec append = fun xs ys ->
if is_empty xs
then ys
else cons (head xs) (append (tail xs) ys)
L'idée est de "déconstruire" xs afin de se retrouver avec une liste vide. Au fur et à mesure, on reconstruit xs élément par élément avant d'y accoler ys lorsque cet objectif est atteint.
- update - Mise à jour d'un nœud
On cherche à changer la valeur x au rang i dans xs par la valeur y.
En impératif, on cherche le nœud concerné et on change la valeur. Le temps d'exécution est d'ordre O(n) dans le pire des cas, mais le xs original est perdu.
En fonctionnel, la méthode de recherche est la même. Le temps d'exécution est toujours d'ordre O(n) dans le pire des cas, mais on récupère ys, reconstruction altérée de xs tout en conservant l'original.
let rec update = fun xs i y ->
if is_empty xs
then raise Index_out_of_bounds (* Si la liste est vide, il n'y a rien à remplacer ! *)
else if i = 0
then cons y (tail xs)
else cons (head xs) (update (tail xs) (i - 1) y)
Comme pour append, on déconstruit puis reconstruit xs, sauf que l'on a un compteur qui est décrémenté de 1 par élément reconstruit. S'il atteint 0, la valeur de l'élément actuel est replacé par y. Si on reconstruit xs dans son intégralité (donc qu'il ne reste que la liste vide) avant que le compteur ait atteint 0, on lève une exception.
- suffixes - Afficher tous les suffixes d'une liste par ordre décroissant de taille
Par exemple, la liste [1, 2, 3, 4] doit retourner [[1, 2, 3, 4], [2, 3, 4], [3, 4], [4], []].
Le temps d'exécution de cette fonction est d'ordre O(n).
let rec suffixes = fun xs ->
if is_empty xs
then nil
else cons xs (suffixes (tail xs))
Ici, on utilise le fait que la fonction tail renvoie toute la liste sauf la tête. Ainsi, on peut accoler tous les suffixes un par un, jusqu'à s'arrêter avec la liste vide.
Arbre de recherche binaire
Il est possible d'utiliser des méthodes de recherche plus complexes lorsque l'on utilise une structure où un élément pointe vers plus qu'un seul autre élément. Prenons par exemple les arbres de recherche binaires.
Un arbre de recherche binaire est un arbre dont les valeurs stockées dans chaque élément sont rangées par ordre symétrique, c'est-à-dire que pour un nœud donné, sa valeur est supérieure à toutes les valeurs stockées dans le sous-arbre de gauche et inférieure à celles dans le sous-arbre de droite.
Dans le code ci-dessous, BalancedTree est un foncteur, autrement dit une fonction qui prendre comme paramètre un module O de type ORDERED.
module BalancedTree(O: ORDERED)= struct
type elem = O.t
type tree = E | T of (tree * elem * tree)
let rec member...
let rec insert...
end;;
Penchons-nous sur les méthodes member et insert.
- member - Vérifie si une valeur est présente dans l'arbre
En reprenant notre type ordonné, on remarque que l'on ne dispose que de 3 fonctions de test, à savoir l'égalité (O.eq), l'infériorité stricte (O.lt) et l'infériorité (O.leq).
Pour construire cette fonction, on serait tenté d'écrire :
let rec member = fun xs x ->
match xs with
| E -> false
| T(e1, y, e2) -> if (O.lt x y)
then member e1 x
else if (O.lt y x)
then member e2 x
else true
On regarde si la valeur du nœud est strictement plus grande que celle recherchée. Si oui, on continue à chercher à gauche. Sinon, on regarde si la valeur du nœud est strictement inférieure à celle recherchée. Si c'est le cas, on poursuit la recherche à gauche. Sinon, il y a égalité et la valeur est bien membre de l'arbre. Si on atteint une feuille sans avoir eu d'égalité, alors la valeur n'appartient pas à l'arbre.
En effet, le pire scénario, ici la branche qui tourne toujours à droite jusqu'au bout de l'arbre, exigerait 2n comparaisons (avec n la profondeur de l'arbre) pour retourner un résultat, étant donné qu'il effectue deux comparaisons par nœud.
let rec member =
let rec member_aux = fun xs aux x ->
match xs with
| E -> O.eq aux x
| T(e1, y, e2) -> if (O.lt x y)
then member_aux e1 aux x
else member_aux e2 y x
in fun xs x ->
match xs with
| E -> false
| T(e1, y, e2) -> if(O.lt x y)
then member e1 x
else member_aux e2 y x
Ici, on fait appel à une fonction auxiliaire itérative stockant une valeur intermédiaire. Cette fonction fait appel au fait que si x n'est pas strictement inférieur à y, alors x est supérieur ou égal à y. Ainsi, on parcourt la branche correspondante comme précédemment, mais on garde ce candidat potentiel jusqu'à ce que l'on atteigne une feuille. Ainsi, on ne réalise dans le pire des cas que n + 1 comparaisons, une par niveau de profondeur et une supplémentaire pour vérifier l'égalité une fois arrivé aux feuilles.
- insert - Insère une valeur dans l'arbre
Pour l'insertion, on procède similairement pour atteindre la feuille correspondante.
let rec insert = fun xs x ->
match xs with
| E -> T(E, x, E)
| T(e1, y, e2) as s -> if (O.lt x y)
then T((insert e1 x), y, e2)
else if (O.lt y x)
then T(e1, y, (insert e2 x))
else s
Comme précédemment, on regarde s'il faut continuer à gauche ou à droite en reconstruisant une copie de l'arbre au fur et à mesure. Cependant, si la valeur à ajouter est déjà présente dans l'arbre, on recopie également ce nœud, ce qui fait que la branche de recherche est testée de la racine à la feuille sans aucun changement à appliquer. En levant une exception si l'on trouve la valeur à ajouter dans l'arbre, on optimise le temps d'exécution en ne faisant pas de copie inutile.
exception Already_there
let rec insert = fun xs x ->
try begin
match xs with
| E -> T(E, x, E)
| T(e1, y, e2) -> if(O.lt x y)
then T((insert e1 x), y, e2)
else if (O.lt y x)
then T(e1, y, (insert e2 x))
else raise Already_there
end with Already_there -> xs
Ainsi, on s'arrête si l'on trouve la valeur à ajouter et l'on retourne une copie de l'arbre tel quel. Et comme pour member, il est possible d'optimiser le nombre de comparaisons, ce qui donne au final une fonction qui ressemble à ceci :
let rec insert =
let rec insert_aux = fun xs aux x ->
match xs with
| E -> if (O.eq aux x)
then raise Already_there
else T(E, x, E)
| T(e1, y, e2) -> if (O.lt x y)
then T((insert_aux e1 aux x), y, e2)
else T(e1, y, (insert_aux e2 y x))
in fun xs x ->
try begin
match xs with
| E -> T(E, x, E)
| T(e1, y, e2) -> if (O.lt x y)
then T((insert e1 x), y, e2)
else T(e1, y, (insert_aux e2 y x))
end with Already_there -> xs
On se retrouve donc avec une fonction d'insertion qui ne copie pas inutilement et qui ne réalise pas plus que n + 1 comparaisons.
Tas gaucher
Un tas est une version d'arbre particulière. En effet, elle se caractérise par le fait que la valeur de chaque nœud ne peut être plus grand que n'importe laquelle de ses enfants. Cette caractéristique fait que l'élément le plus petit se trouve toujours à la racine.
Un tas est dit gaucher si le rang de n'importe quel enfant de gauche est supérieur ou égal à celui de l'enfant de droit qui lui est associé. On appelle rang d'un nœud la longueur de sa colonne vertébrale droite, c'est-à-dire le chemin le plus à droite qui va de ce nœud à une feuille. Une conséquence simple de cette propriété est que la colonne vertébrale droite d'un nœud constitue le chemin le plus court de ce nœud à une feuille.
Soit r le rang de la racine d'un tas gaucher de taille n. On peut en déduire que chaque nœud de profondeur inférieure ou égale à r-1 a exactement deux enfants, car sinon r aurait une valeur plus faible ou la propriété gauchère ne serait pas respectée. Ainsi, on peut affirmer que la taille d'un tas est donc d'au moins 2r - 1. De ce fait, on peut en déduire que le rang de la racine vaut au plus log(n + 1). Par conséquent, la colonne vertébrale droite d'un tas gaucher de taille n comporte au plus ⌊log(n + 1)⌋ éléments.
Code de la structure tas gaucher
module LeftistHeap (O: ORDERED) = struct
type elem = O.t
type heap = Nil | Cons of (int * heap * elem * heap)
let rank = fun h ->
match h with
| Nil -> 0
| Cons(r, _, _, _) -> r
let makeH...
let merge...
let insert...
exception EmptyHeap
let findMin...
let deleteMin...
end;;
Ici, nous allons étudier les fonctions merge, insert, findMin et deleteMin.
- merge - Fusionne deux tas
Afin de simplifier l'opération, on remarque que la colonne vertébrale droite d'un tas gaucher est ordonnée. On en déduit que le concept clé est de fusionner les colonnes vertébrales des deux tas comme on fusionnerait deux listes triées avant d'échanger les enfants le long de la branche afin de restaurer la propriété gauchère.
Comme il a été démontré précédemment que la longueur de la colonne vertébrale est au plus logarithmique, on peut en déduire que merge a un temps d'exécution d'ordre O(log n).
let makeH = fun v a b ->
if rank a >= rank b
then Cons(rank b + 1, a, v, b)
else Cons(rank a + 1, b, v, a)
let rec merge = fun x y ->
match x, y with
| Nil, _ -> y
| _, Nil -> x
| Cons(_, e11, v1, e12), Cons(_, e21, v2, e22) -> if (O.leq v1 v2)
then makeH v1 e11 (merge e12 y)
else makeH v2 e21 (merge x e22)
Ici, on fait appel à une fonction intermédiaire : makeH.
Cette fonction compare le rang des deux tas et échange les enfants si besoin afin de respecter la propriété gauchère.
Ensuite, concernant merge en elle-même, on compare les valeurs des deux racines et on fait appel à makeH pour combiner et potentiellement échanger les enfants.
- insert - Insère une valeur dans l'arbre
Une fois merge défini, il suffit d'établir que l'on veut fusionner le tas avec un tas d'une seule valeur. Et puisque le temps d'exécution de merge est d'ordre O(log n), il en va de même pour insert.
let insert = fun v h -> (merge (Cons(1, Nil, v, Nil)) h)
- findMin - Récupère le minimum
Comme le minimum est par définition à la racine, le temps d'exécution de findMin est d'ordre O(1), donc constant.
let findMin = fun h ->
match h with
| Nil -> raise EmptyHeap
| Cons(_, _, v, _) -> v
- deleteMin - Supprime le minimum
Similairement, le minimum étant à la racine, on peut établir que le supprimer revient à fusionner ses enfants. De plus, merge ayant un temps d'exécution d'ordre O(log n), celui de deleteMin est le même.
let deleteMin = fun h ->
match h with
| Nil -> raise EmptyHeap
| Cons(_, a, _, b) -> merge a b
Tas binomial
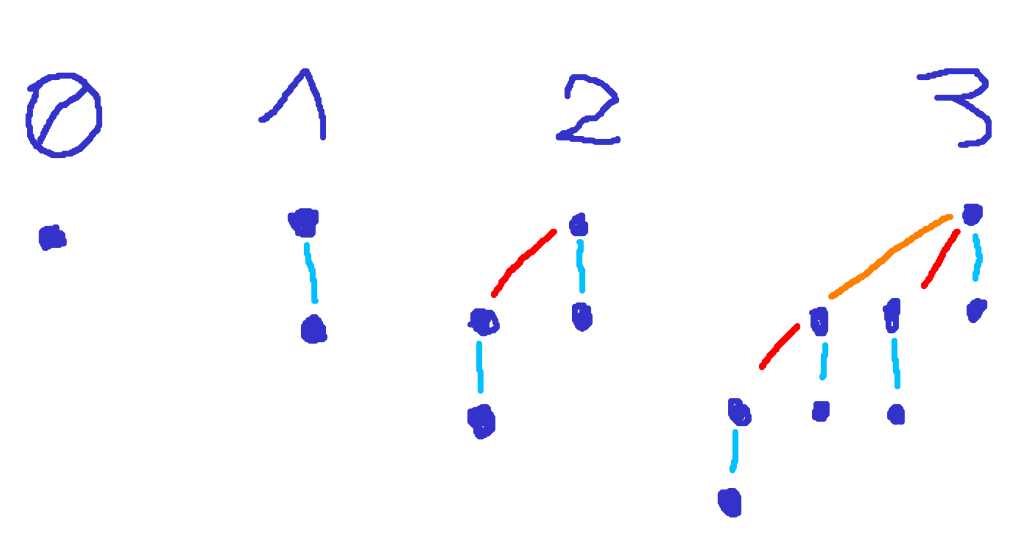
Les tas binomiaux sont des tas composés d'un type plus primitif appelé arbre binomial. Les arbres binomiaux sont défini inductivement comme suit :
- Un arbre binomial de rang 0 est un singleton de nœud ;
- Un arbre binomial de rang r est formé en liant deux arbres binomiaux de rang r-1 tel qu'un des arbres devient l'enfant le plus à gauche de l'autre.
De cette définition, on comprend qu'un arbre binomial de rang r contient exactement 2r nœuds.
Il existe une deuxième définition équivalente des arbres binomiaux :
- Un arbre binomial de rang r est un nœud ayant r enfants t1 à tr où chaque enfant ti est un arbre binomial de rang r - i.
Dans le code ci-dessous, on représente un nœud dans un arbre binomial comme un élément avec une liste de ses enfants. Par commodité, on note aussi le rang de chaque nœud.
De plus, un tas binomial étant une liste d'arbres binomiaux ne pouvant comporter qu'un seul arbre d'un rang donné et un arbre binomial de rang r comportant 2r éléments, on constate alors que les arbres d'un tas binomial de taille n correspondent à la représentation binaire de n.
Par exemple, la représentation binaire de 13 est 1101, donc un tas binomial de taille 13 contient un arbre de rang 0, un de rang 2 et un de rang 3 (de taille respective 1, 4 et 8). De plus, comme la représentation binaire de n contient au plus ⌊log(n + 1)⌋ bits à 1, un tas binomial de taille n contient au plus ⌊log(n + 1)⌋ arbres.
module BinomialHeap (O: ORDERED) = struct
type elem = O.t
type tree = Node of (int * elem * tree list)
type heap = tree list
exception EmptyHeap
let rank (Node(r, _, _)) = r
let root (Node(_, x, _)) = x
let link = ...
let rec insTree...
let insert = ...
let rec merge...
let rec removeMinTree...
let findMin = ...
let deleteMin = ...
end;;
Les fonctions que nous allons étudier ici sont link, insert, merge, findMin et deleteMin.
- link - Lie deux arbres de même rang pour en construire un de rang supérieur
Les arbres étant triés en respectant la propriété du tas, il suffit de comparer les racines pour voir lequel reste au sommet en les liant, l'autre étant ajouté à la liste des enfants.
let link = fun (Node(r, x1, c1) as t1) (Node(_, x2, c2) as t2) ->
if (O.leq x1 x2)
then Node(r + 1, x1, t2 :: c1)
else Node(r + 1, x2, t1 :: c2)
- insert - Insertion d'un élément
Les fonctions insert et merge sont toutes deux vaguement comparables à l'addition de deux nombres binaires. Pour insérer un nouvel élément, on crée un singleton d'arbre (donc de rang 0) puis on parcourt tous les arbres du tas par ordre croissant de rang jusqu'à trouver un rang manquant en liant les arbres de rang égal en chemin. On peut comparer le lien à une retenue arithmétique.
let rec insTree = fun t ls ->
match ls with
| [] -> [t]
| t' :: ts' as ts -> if rank t < rank t'
then t :: ts
else insTree (link t t') ts'
let insert = fun x ts -> insTree (Node(0, x, [])) ts
Le pire scénario étant dans un tas de taille n = 2k - 1 qui nécessiterait k liens, donnant un temps d'exécution d'ordre O(log n).
- merge - Fusion de deux tas
Comme précédemment, merge parcourt la liste d'arbres de chaque tas par ordre croissant de rang en liant les arbres de rang égal.
let rec merge = fun ts1 ts2 ->
match ts1, ts2 with
| _, [] -> ts1
| [], _ -> ts2
| t1 :: ts1', t2 :: ts2' -> if rank t1 < rank t2
then t1 :: (merge ts1' ts2)
else if rank t2 < rank t1
then t2 :: (merge ts1 ts2')
else insTree (link t1 t2) (merge ts1' ts2')
- findMin et deleteMin - Trouve et supprime le minimum respectivement
Ces deux fonctions ont besoin de la même fonction auxiliaire, à savoir removeMinTree, qui trouve l'arbre avec la plus petite valeur et l'extrait de la liste, retournant à la fois l'arbre et le reste de la liste.
let rec removeMinTree = fun ls ->
match ls with
| [] -> raise EmptyHeap
| [t] -> (t, [])
| t :: ts -> let (t', ts') = removeMinTree ts in
if (O.leq (root t) (root t'))
then (t, ts)
else (t', t :: ts')
let findMin = fun ts -> let (t, _) = removeMinTree ts in root t
let deleteMin = fun ts -> let (Node(_, x, ts1), ts2) = removeMinTree ts in merge (rev ts1) ts2
À partir de là, findMin retourne juste la racine de l'arbre. Cependant, deleteMin est plus complexe. En effet, après avoir retiré la racine de l'arbre, il faut remettre la liste d'enfants de l'arbre avec le reste de la liste des arbres. Cela dit, bien que chaque liste d'enfants est une collection d'arbres binomiaux de rang unique, ceux-ci sont triés par ordre décroissant de rang et non par ordre croissant. Afin de convertir cette liste en tas binomial valide, on l'inverse à l'aide de la fonction rev avant de la fusionner avec les arbres restants.
Arbre rouge / noir
Précédemment, nous avons vu les arbres de recherche binaires. Bien que cette structure fonctionne bien avec des données aléatoires ou désordonnées, leur performance est grandement réduite avec des données ordonnées car toutes les opérations ont un temps d'exécution d'ordre allant jusqu'à O(n). Une solution à ce problème est de garder chaque arbre relativement équilibré. Ainsi, aucune opération n'a de temps d'exécution d'ordre excédant O(log n). Une famille d'arbres de recherche binaires équilibrés populaire est celle des arbres bicolores, ou arbres rouge-noir.
Un arbre bicolore est un arbre binaire dont chaque nœud a une couleur, rouge ou noir. On considère qu'un nœud vide est noir. De plus, un arbre bicolore doit respecter deux invariants :
- Aucun nœud rouge ne peut avoir d'enfant rouge.
- Toutes les branches allant de la racine à une feuille doivent avoir le même nombre de nœuds noirs.
De ces deux invariants, on peut extraire que le chemin le plus long - alternant nœuds noirs et rouge - est au plus deux fois plus long que le chemin le plus court - composé uniquement de nœuds noirs. En reprenant la démonstration faite sur la longueur de la colonne vertébrale d'un tas gaucher, on sait que le chemin le plus court d'un arbre de profondeur n contient au plus ⌊log(n + 1)⌋ éléments. Par conséquent, on peut en déduire que le chemin le plus long contient au plus 2⌊log(n + 1)⌋ éléments.
module RedBlackTree(O: ORDERED)= struct
type elem = O.t
type color = R | B
type tree = E | T of (color * tree * elem * tree)
let balance...
let rec member = fun x t ->
match t with
| E -> false
| T(_, e1, y, e2) -> if (O.lt x y)
then member x a
else if (O.lt y x)
then member x b
else true
let rec insert...
end;;
Ici, nous allons étudier les fonctions insert et balance. Mis à part le caractère générique pour la couleur, member fonctionne comme pour les arbres binaires non équilibrés.
- insert - Insertion d'une nouvelle valeur dans l'arbre
La différence majeure entre cette fonction et sa variante pour les arbres non équilibrés relève du respect des invariants.
let insert = fun x t ->
let fun ins = function E -> T(R, E, x, E)
| T(color, e1, y, e2) as t' -> if (O.lt x y)
then balance (color, ins a, y, b)
else if (O.lt y x)
then balance (color, a, y, ins b)
else t'
in let T(_, e1, y, e2) = ins t
in T(B, e1, y, e2)
Cette fonction étend la variante non équilibrée sur trois axes majeurs : Premièrement, quand on crée un nouveau nœud, on le colore initialement en rouge. Deuxièmement, on force le nœud final à être noir, indépendamment de la couleur retournée par la fonction ins. Enfin, on replace les appels au constructeur T par des appels à la fonction balance, chargée de construire un nœud tout en modifiant l'arbre pour respecter les invariants d'équilibre.
- balance - Équilibrage de l'arbre selon les invariants
En donnant la couleur rouge à un nouveau nœud, on maintient l'invariant 2 mais viole l'invariant 1 à chaque fois que le parent est rouge. Pour ce faire, on autorise une violation rouge-rouge à la fois que l'on fait remonter le long de la branche de recherche vers la racine en équilibrant. La fonction balance détecte une violation rouge-rouge quand il voit une suite noir-rouge-rouge et la corrige (voir figure ci-dessous).
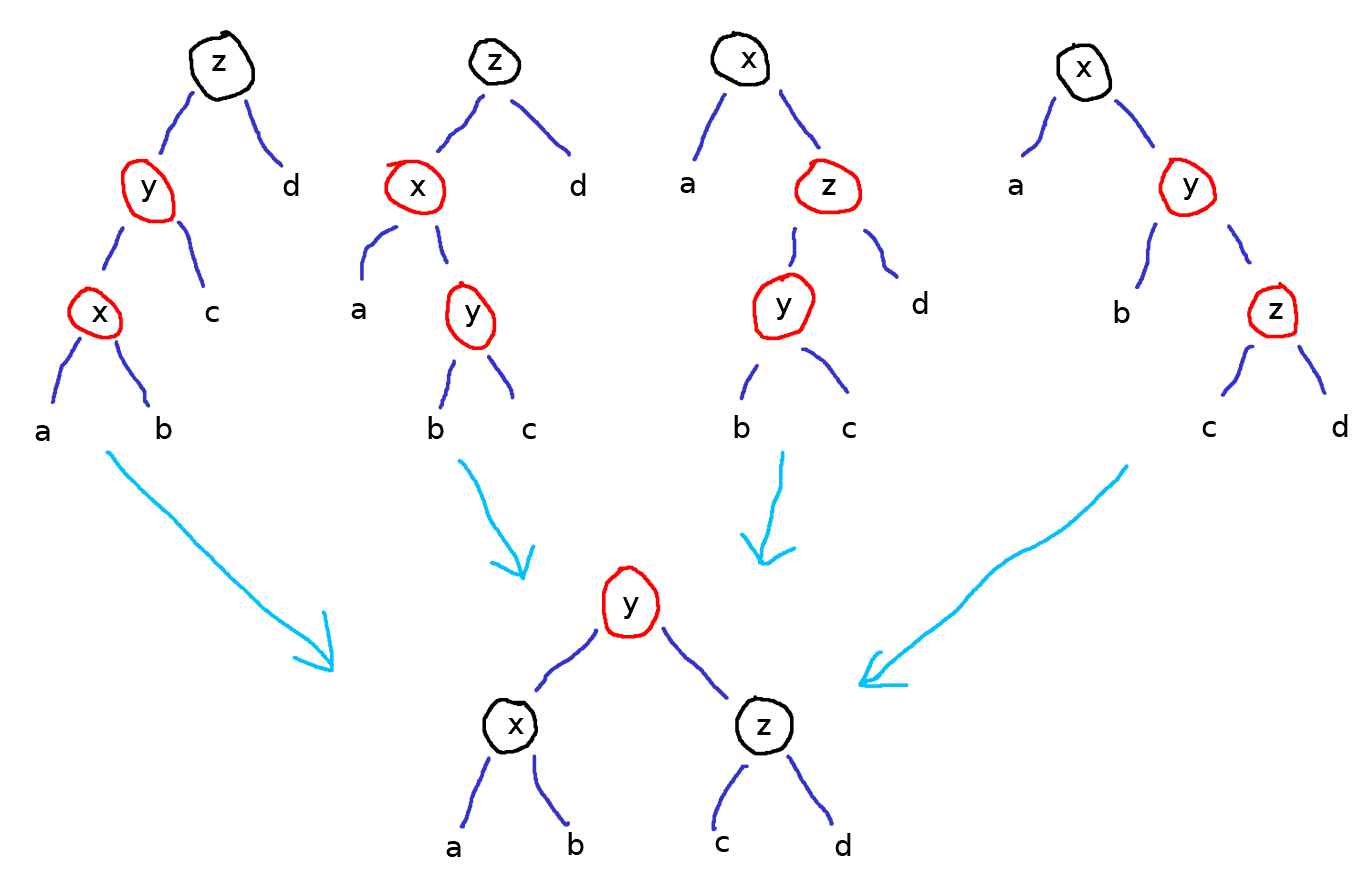
Ici, le code essaie de trouver l'un des quatre cas noir-rouge-rouge ne respectant pas l'invariant 1, puis de le corriger. Si aucun cas n'est trouvé, alors on construit le sous-arbre tel quel.
let balance = function
(B,T (R,T (R,a,x,b),y,c),z,d) -> T (R,T (B,a,x,b),y,T (B,c,z,d))
| (B,T (R,a,x,T (R,b,y,c)),z,d) -> T (R,T (B,a,x,b),y,T (B,c,z,d))
| (B,a,x,T (R,T (R,b,y,c),z,d)) -> T (R,T (B,a,x,b),y,T (B,c,z,d))
| (B,a,x,T (R,b,y,T(R,c,z,d))) -> T (R,T (B,a,x,b),y,T (B,c,z,d))
| (c,a,x,b) -> T (c,a,x,b)
Évolution du domaine de recherche
Après s'être penché en détail sur la thèse d'Okasaki, voici quelques articles plus récents en rapport avec le sujet permettant d'élargir la question.
- Manufacturing Datatypes par Ralf Hinze, publié en 1999 et édité par Okasaki traitant d'une structure générale pour construire des structures de données purement fonctionnelles permettant de satisfaire des contraintes de taille ou de forme, notamment pour l'implémentation de matrices et de certains types d'arbres.
- Scrap your boilerplate: a practical design pattern for generic programming de Ralf Lämmel et Simon Peyton-Jones proposant un modèle de métastructure, c'est-à-dire (une structure permettant de générer du code ?), afin de remédier à l'usage de code passe-partout, autrement dit du code répété à plusieurs reprises avec très peu de modifications.
- Finger trees: a simple general-purpose data structure de Ralf Hinze et Ross Paterson introduisant une nouvelle structure : les arbres pointés 2-3 permettant d'accéder aux feuilles dans un laps de temps amorti constant. Cette structure peut servir de base pour plusieurs autres structures de données.
- Parallel Concurrent ML de John Reppy, Claudio V. Russo et Yingqi Xiao présentant le langage fonctionnel concurrent CML (pour Concurrent ML), c'est-à-dire que le programme peut utiliser plusieurs processus simultanément, réduisant le temps d'exécution.
Sources et annexes
Sources
Annexes