« Complexité pratique contre complexité théorique » : différence entre les versions
Aucun résumé des modifications |
|||
| (63 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 7 : | Ligne 7 : | ||
Cette courbe va ainsi nous éclairer sur le comportement asymptotique de l'algorithme.<br> |
Cette courbe va ainsi nous éclairer sur le comportement asymptotique de l'algorithme.<br> |
||
Ce comportement asymptotique représente le comportement général de la fonction de la complexité (souvent impossible à calculer de manière exacte). <br> |
Ce comportement asymptotique représente le comportement général de la fonction de la complexité (souvent impossible à calculer de manière exacte). <br> |
||
Cette approximation est généralement représentée par <math>O(f(n))</math>, ou f(n) représente une fonction telle que pour n -><math>+\infty</math>, <math>\frac{c(n)}{f(n)}= |
Cette approximation est généralement représentée par <math>O(f(n))</math>, ou f(n) représente une fonction telle que pour n -><math>+\infty</math>, <math>\frac{c(n)}{f(n)}=1</math> (où c(x) représente la fonction de la complexité dans le pire des cas: plus d'opérations possibles a effectuer).<br> |
||
Ce comportement asymptotique peut être analysé sous deux différents point de vue: <br> |
Ce comportement asymptotique peut être analysé sous deux différents point de vue: <br> |
||
Le point de vue théorique, qui va analyser le comportement générale de deux complexité et déduire laquelle des deux est la moins complexe en prenant la valeur vers laquelle tend O(f(n)) pour <math>+\infty</math>.<br> |
Le point de vue théorique, qui va analyser le comportement générale de deux complexité et déduire laquelle des deux est la moins complexe en prenant la valeur vers laquelle tend O(f(n)) pour <math>+\infty</math>.<br> |
||
| Ligne 49 : | Ligne 49 : | ||
return res |
return res |
||
</pre> |
</pre> |
||
La fonction "entiersdicho" permet de rechercher dans un tableau donné en paramètre, un élément de manière dichotomique. |
La fonction "entiersdicho" permet de rechercher dans un tableau trié donné en paramètre, un élément de manière dichotomique.<br> |
||
On definit la valeur du milieu du tableau ((borne supérieure + borne inférieure)//2). On regarde ensuite si l'entier recherché est inférieur supérieur ou égal à la valeur du milieu : <br> |
|||
Si la valeur du milieu est inférieur à l'entier, on recommence la recherche avec cette fois ci, la borne supérieur égale à la valeur précédente du milieu.<br> |
|||
Si la valeur du milieu est supérieur à l'entier, on recommence la recherche avec cette fois ci, la borne inférieur égale à la valeur précédente du milieu.<br> |
|||
Enfin si la valeur du milieu est égale à l'entier, on renvoi la valeur du milieu (position dans le tableau).<br> |
|||
<br> |
<br> |
||
[[Fichier: |
[[Fichier:Dicho10000.PNG]] <br> |
||
Une fois que l'on trace la complexité de la fonction, on observe une forme logarithmique c'est à dire <math>O(log(x))</math> |
|||
== tri de tableau: main/python == |
== tri de tableau: main/python == |
||
Un deuxième cas d'étude est la comparaison entre la complexité d'une fonction de tri par la méthode du "tri à bulle" et de la fonction de tri de python : sorted(). |
|||
<pre> |
<pre> |
||
def echange(tab, i , j): |
def echange(tab, i , j): |
||
| Ligne 81 : | Ligne 87 : | ||
return res |
return res |
||
</pre> |
</pre> |
||
Ici, la fonction "triabulle" va parcourir le tableau jusqu'à tomber sur une valeure supérieure à la suivante. Dans ce cas elle va échanger ces deux valeurs. Si à la fin du tableau aucun élément n'a été échangé, la fonction renvoi le tableau désormais trié, sinon, elle refait un tour. |
|||
[[Fichier:Bulle500.PNG]] |
|||
[[Fichier: |
[[Fichier:Bulle500.PNG]] fonction "triabulle" <br> |
||
[[Fichier:Python500.PNG]] fonction "sorted()" de python <br> |
|||
En étudiant ces deux fonctions on remarque que leurs formes générales sont relativement identiques (<math>O(exp(x))</math>) mais que la fonction "sorted()" prends un temps bien inférieur à s'exécuter que "triabulle()". On peut donc conclure qu'au point de vue théorique, ces deux formules sont équivalente, mais au point de vue pratique, on va privilégier l'utilisation de "sorted()" car pour la même croissance en fonction de la taille du tableau, elle met beaucoup moins de temps à s'exécuter (ce qui est dû à la compilation de python bien plus efficace sur une fonction déjà incluse dans le langage). |
|||
== |
== médiane == |
||
Comparer la médiane de python à la médiane dite naïve revient a comparer la complexité des deux différents tri. Effectivement les deux fonctions prennent la valeur du milieu sur un tableau trié (grâce aux fonctions de tri vu précédemment) afin de retourner la médiane. |
|||
<pre> |
<pre> |
||
def medianenaive(tab): |
def medianenaive(tab): |
||
| Ligne 96 : | Ligne 105 : | ||
return median(tab) |
return median(tab) |
||
</pre> |
</pre> |
||
[[Fichier:Compairaisonmednaive-medpy10essais.PNG]] |
|||
== medianes des medianes, quickselect == |
== medianes des medianes, quickselect == |
||
L'algorithme de Quickselect est un algorithme permettant de retrouver l'indice nième d’un tableau non trié. Pour cela on prend aléatoirement un élément du tableau et on le compare avec les autres éléments du tableau en créant ainsi deux nouveaux tableaux : les entier supérieurs et les entiers inférieurs à l'élément.<br> |
|||
'''quickselect :''' |
|||
Si l'indice recherché est supérieur ou égal à la taille des inférieurs et est inférieur à la taille du tableau moins la taille des supérieurs alors il s'agit de l'élément.<br> |
|||
Sinon, si l'indice est inférieur au tableau des éléments inférieurs on rappel la fonction avec cette fois ci en entrée le tableau des inférieurs et l'indice. Dans le dernier cas, on rappel la fonction avec en entrée le tableau des supérieurs et l'indice moins la taille du tableau auquel on a ajouté la taille des supérieurs. |
|||
<br>'''quickselect :''' |
|||
<pre> |
<pre> |
||
def quickselectmed(tab): |
def quickselectmed(tab): |
||
| Ligne 106 : | Ligne 118 : | ||
indicemed = taille//2 |
indicemed = taille//2 |
||
valmed = cherchevalind(tab,indicemed) |
valmed = cherchevalind(tab,indicemed) |
||
return valmed |
|||
return valmed, t[len(t)//2] |
|||
def cherchevalind(tab,indice): |
def cherchevalind(tab,indice): |
||
| Ligne 125 : | Ligne 136 : | ||
return cherchevalind(sup,indice - len(tab) + len(sup)) |
return cherchevalind(sup,indice - len(tab) + len(sup)) |
||
</pre> |
</pre> |
||
L'algorithme de la médiane des médianes est une variante de l'algorithme du quickselect où l'élément aléatoire du tableau est remplacé par la valeur médiane des différentes médianes des paquets de cinq éléments du tableau. |
|||
'''Medianes des medianes :''' |
|||
Pour ce faire on sépare le tableau en paquets de cinq éléments. On crée ensuite un nouveau tableau comprenant les médianes des différents paquets. S'il n'y a qu'un élément au sein de ce tableau alors il s'agit de l'élément à appliquer au quickselect. Sinon on recommence l'opération avec ce nouveau tableau. |
|||
<br>'''Médianes des médianes :''' |
|||
<pre> |
<pre> |
||
def medianemediane(tab): |
def medianemediane(tab): |
||
| Ligne 164 : | Ligne 177 : | ||
return cherchevalind(sup,indice - len(tab) + len(sup)) |
return cherchevalind(sup,indice - len(tab) + len(sup)) |
||
</pre> |
</pre> |
||
<br> |
|||
[[Fichier:Tabnontri1000medpymedmedquick.PNG]] |
|||
<br>Ces courbes représentent la comparaison de la complexité de la médiane python (en haut), de la médiane des médianes (au milieu) et du quickselect (en bas) afin de retrouver la valeur médiane d'un tableau non trié (sur 1000 essais). On peut voir que la complexité de la médiane des médianes et du quickselect ont une forme linéaire, <math>O(n)</math>. <br> |
|||
On peut donc en conclure que d'un point de vue théorique les algorithmes de la médiane des médianes et du quick select sont à privilégiés, mais d'un point de vue pratique, la médiane de python prends beaucoup moins de temps à s'exécuter même pour des valeurs de tableaux élevés.<br> |
|||
[[Fichier:Tabtri1000medpymedmedquick.PNG]] |
|||
<br>Ces courbes représentent la comparaison de la complexité de la médiane python (en haut), de la médiane des médianes (au milieu) et du quickselect (en bas) afin de retrouver la valeur médiane d'un tableau trié (sur 1000 essais).On remarque que d'un point de vue théorique, que le tableau soit trié ou non trié la complexité reste la même, mais d'un point de vue pratique on remarque que la médiane de python prend beaucoup moins de temps à s'exécuter sur un tableau déjà trié. |
|||
== Multiplication naive / Karatsuba == |
== Multiplication naive / Karatsuba == |
||
L'algorithme de Karatsuba est un algorithme de type "diviser pour mieux régner" permettant de réduire le nombre de calcul lors de la multiplication de grands entiers de même taille.<br> |
|||
'''Multiplication naive:''' |
|||
Dans un premier cas on observe si l'un des deux entiers a une taille de un, c'est à dire est un unique chiffre. Dans ce cas on applique tout simplement la multiplication dite naïve (chaque élément du nombre par le chiffre).<br> |
|||
Sinon, on sépare chacun des deux nombres en deux créant quatre nouveaux entiers "a", "b", "c" et "d". |
|||
<pre> |
<pre> |
||
Par exemple pour 1234 * 4567 on crée: |
|||
a = 12 , b = 34 , c = 45 et d = 67 |
|||
</pre> |
|||
Ensuite, on peut appliquer deux différents calculs:<br> |
|||
-Le calcul dit naïf où on effectue quatre appels récursifs (ac, ad, bc et bd) afin de simplifier le calcul |
|||
<math>(a * 10^{k} + b)(c*10^{k} + d)</math> par: <br> <math> ac * 10^{2k} + (ad + bc) * 10^{k} + bd </math><br> |
|||
-Le calcul de Karatsuba avec plus que trois appels récursifs (ac, bd et <math>(a-d)*(c-d)</math>):<br> |
|||
<math>ac * 10^{2k} + (ac + bd - (a-b)(c-d))* 10^{k}+ bd</math> |
|||
<br>'''Multiplication naive:''' |
|||
<pre> |
|||
def multint(T,a): |
|||
val = multscalaireT(T,a) |
|||
res = 0 |
|||
for i in range (0,len(val)): |
|||
res = res + val[i] * 10 ** (len(val)-1 - i) |
|||
return int(res) |
|||
def multscalaireT(T,a): |
def multscalaireT(T,a): |
||
return [T[i] * a for i in range (len(T))] |
return [T[i] * a for i in range (len(T))] |
||
| Ligne 184 : | Ligne 222 : | ||
return res |
return res |
||
</pre> |
</pre> |
||
[[Fichier:Multinaive1000.png]]<br> |
|||
On remarque la complexité de la multiplication naive : <math>(a * 10^{k} + b)(c*10^{k} + d)</math> est linéaire. |
|||
'''Karatsuba''' |
|||
<br>'''Karatsuba à quatre appels récursifs:''' |
|||
<pre> |
<pre> |
||
def karatsubanaive(nb1,nb2): |
def karatsubanaive(nb1,nb2): |
||
'''Entrée: deux tableaux, Sortie: un |
'''Entrée: deux tableaux, Sortie: un entier''' |
||
taillenb1 = len(nb1) |
taillenb1 = len(nb1) |
||
taillenb2 = len(nb2) |
taillenb2 = len(nb2) |
||
if ( taillenb1 == 1): |
if ( taillenb1 == 1): |
||
return |
return multint(nb2,nb1[0]) |
||
elif( taillenb2 == 1) : |
elif( taillenb2 == 1) : |
||
return |
return multint(nb1,nb2[0]) |
||
return multnaive(nb1,nb2) |
return multnaive(nb1,nb2) |
||
else : |
else : |
||
mil1=len(nb1)//2 |
mil1=len(nb1)//2 |
||
mil2=len(nb2)//2 |
mil2=len(nb2)//2 |
||
a= |
a=nb1[:mil1] |
||
b= |
b=nb1[mil1:] |
||
c= |
c=nb2[:mil2] |
||
d= |
d=nb2[mil2:] |
||
elmt1 = |
elmt1 = karatsubanaive(a,c) |
||
elmt2 = |
elmt2 = karatsubanaive(a,d) |
||
elmt3 = |
elmt3 = karatsubanaive(b,c) |
||
elmt4 = |
elmt4 = karatsubanaive(b,d) |
||
return resultatkaratsuban(elmt1,elmt2,elmt3,elmt4) |
return resultatkaratsuban(elmt1,elmt2,elmt3,elmt4,taillenb1) |
||
def resultatkaratsuban(elmt1,elmt2,elmt3,elmt4,taillenb1): |
|||
return (elmt1*10**((taillenb1-1)*2)) + ((elmt2 + elmt3) * 10**(taillenb1-1)) + elmt4 |
|||
</pre> |
|||
[[Fichier:Karanaive1000.PNG]]<br> |
|||
La complexité théorique de cet algorithme "karatsuba naïf est la même que la complexité de la multiplication "naïve". |
|||
<pre> |
|||
def karatsuba(nb1,nb2): |
|||
'''Entrée: deux tableaux, Sortie: un tableau)''' |
|||
taillenb1 = len(nb1) |
|||
taillenb2 = len(nb2) |
|||
if (taillenb1 == 0) or (taillenb1 == 0): |
|||
return 0 |
|||
elif ( taillenb1 == 1): |
|||
return multint(nb2,nb1[0]) |
|||
elif( taillenb2 == 1) : |
|||
return multint(nb1,nb2[0]) |
|||
else : |
|||
mil1=len(nb1)//2 |
|||
mil2=len(nb2)//2 |
|||
a=nb1[:mil1] |
|||
b=nb1[mil1:] |
|||
c=nb2[:mil2] |
|||
d=nb2[mil2:] |
|||
sousab = soustraction(a,b) |
|||
souscd = soustraction(c,d) |
|||
elmt1 = karatsuba(a,c) |
|||
elmt2 = karatsuba(b,d) |
|||
elmt3 = karatsuba(sousab,souscd) |
|||
return resultatkaratsuba(elmt1,elmt2,elmt3,taillenb1) |
|||
def soustraction(tab1,tab2): |
|||
nb1 = 0 |
|||
nb2 = 0 |
|||
for i in range (0, len(tab1)-1): |
|||
nb1 = nb1*10 + tab1[i] |
|||
for j in range (0, len(tab2)-1): |
|||
nb2 = nb2*10 + tab2[j] |
|||
res = nb1 - nb2 |
|||
tab = [] |
|||
while res > 0: |
|||
reste = res//10 |
|||
val = res - (reste*10) |
|||
tab = tab + [val] |
|||
res = reste |
|||
return tab |
|||
def resultatkaratsuba(elmt1,elmt2,elmt3,taillenb1): |
|||
res = (elmt1 * 10**((taillenb1-1)*2)) + (elmt1 + elmt2 - elmt3)*10**(taillenb1-1) + elmt2 |
|||
return res |
|||
</pre> |
</pre> |
||
[[Fichier:Kara1000.PNG]]<br> |
|||
On remarque donc que ces trois algorithmes ont une complexité linéaire, mais que la complexité l'algorithme de Karatsuba à trois appels récursifs croît beaucoup moins vite. |
|||
---- |
|||
CONNETABLE Theo (Tuteur : HYVERNNAT Pierre) |
|||
Dernière version du 13 mai 2021 à 17:26
Principe de la complexité
La complexité en algorithmique sert à montrer l'efficacité d'un algorithme, en fonction de plusieurs facteurs comme son temps d'exécution, l'espace qu'il occupe dans la mémoire... (ces facteurs sont en générale induits par le nombre d'opérations qu'effectue l'algorithme).
Afin de mesurer et de représenter cette complexité, on représente l'évolution du temps d'exécution d'une même fonction en fonction de la taille de ses arguments.
On va donc, la plupart du temps utiliser des tableaux en entrée des fonctions, et faire évoluer leurs tailles afin d'obtenir la courbe de leur complexité.
Cette courbe va ainsi nous éclairer sur le comportement asymptotique de l'algorithme.
Ce comportement asymptotique représente le comportement général de la fonction de la complexité (souvent impossible à calculer de manière exacte).
Cette approximation est généralement représentée par Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle O(f(n))}
, ou f(n) représente une fonction telle que pour n ->, Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \frac{c(n)}{f(n)}=1}
(où c(x) représente la fonction de la complexité dans le pire des cas: plus d'opérations possibles a effectuer).
Ce comportement asymptotique peut être analysé sous deux différents point de vue:
Le point de vue théorique, qui va analyser le comportement générale de deux complexité et déduire laquelle des deux est la moins complexe en prenant la valeur vers laquelle tend O(f(n)) pour Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle +\infty}
.
Le point de vue pratique, qui, quand à lui va analyser le comportement générale de deux complexité en fonction d'une taille de tableau limité par l'utilisation régulière de la fonction ou capacité à traiter les information de
l'ordinateur.
Etudes d'algorithmes
Afin de mesurer la complexité avec le langage python, on utilise généralement une fonction essentielle, la bibliotheque "timeit".
import timeit
def chronoquick(tab,nessais):
'''Entrées: un tableau et un entier, Sortie: un entier'''
res = timeit.timeit("quickselectmed("+ str (tab)+")","from __main__ import quickselectmed" , number= nessais)
return res
La fonction timeit.timeit permet de mesurer le temps d'exécution de la fonction entrée (ici quickselectmed(tab)) en fonction d'un nombre d'essais défini. Plus ce nombre d'essais est grand, plus le taux d'erreur sur la forme générale de la courbe sera réduit.
dichotomie
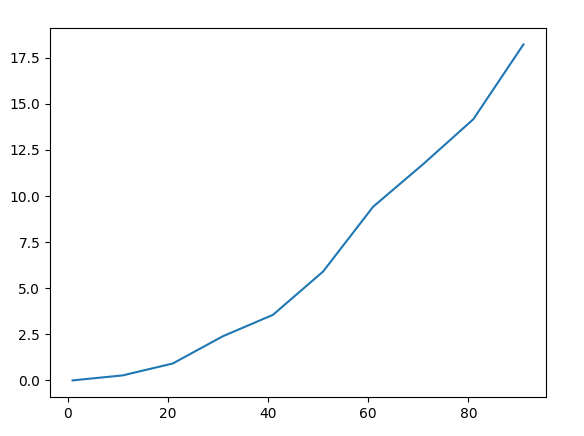
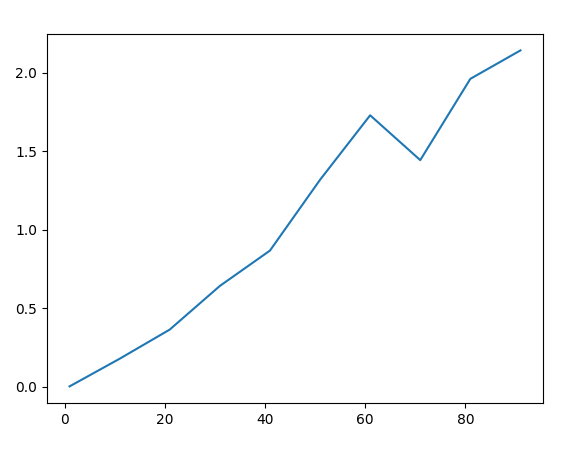
Le premier cas où nous allons analyser la complexité est un algorithme de dichotomie.
def entiersdicho(tab, entier):
'''Entrée: tab un tableau, entier un entier
Sortie: res un entier (position de l'entier dans le tableau'''
b_inf = 0
b_sup = len(tab)
while b_inf <= b_sup and b_inf < len(tab) :
mil =(b_sup + b_inf)//2
if tab[mil] > entier :
b_sup = mil
elif tab[mil] == entier:
return mil
else:
b_inf = mil + 1
return -1
def cherchetab(tab):
entier = randint(0,len(tab))
res = entiersdicho(tab, entier)
return res
La fonction "entiersdicho" permet de rechercher dans un tableau trié donné en paramètre, un élément de manière dichotomique.
On definit la valeur du milieu du tableau ((borne supérieure + borne inférieure)//2). On regarde ensuite si l'entier recherché est inférieur supérieur ou égal à la valeur du milieu :
Si la valeur du milieu est inférieur à l'entier, on recommence la recherche avec cette fois ci, la borne supérieur égale à la valeur précédente du milieu.
Si la valeur du milieu est supérieur à l'entier, on recommence la recherche avec cette fois ci, la borne inférieur égale à la valeur précédente du milieu.
Enfin si la valeur du milieu est égale à l'entier, on renvoi la valeur du milieu (position dans le tableau).
Une fois que l'on trace la complexité de la fonction, on observe une forme logarithmique c'est à dire Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle O(log(x))}
tri de tableau: main/python
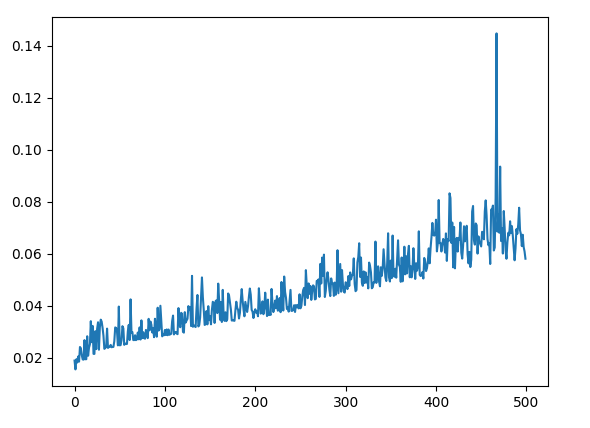
Un deuxième cas d'étude est la comparaison entre la complexité d'une fonction de tri par la méthode du "tri à bulle" et de la fonction de tri de python : sorted().
def echange(tab, i , j):
'''Entrée: tableau, deux entier i et j, Sortie: tableau '''
val_i=tab[i]
val_j=tab[j]
tab[i] = val_j
tab[j] = val_i
return tab
def triabulle(tab):
'''Entrée : un entier, Sortie: un tableau'''
fini = False
while fini == False:
nbechanges = 0
for i in range (0,len(tab)-1):
if (tab[i]> tab[i+1]):
echange (tab, i , i+1)
nbechanges = nbechanges + 1
if nbechanges == 0:
fini = True
return tab
def tripython(tab):
'''Entrée : un entier, Sortie: un tableau'''
res = sorted(tab)
return res
Ici, la fonction "triabulle" va parcourir le tableau jusqu'à tomber sur une valeure supérieure à la suivante. Dans ce cas elle va échanger ces deux valeurs. Si à la fin du tableau aucun élément n'a été échangé, la fonction renvoi le tableau désormais trié, sinon, elle refait un tour.
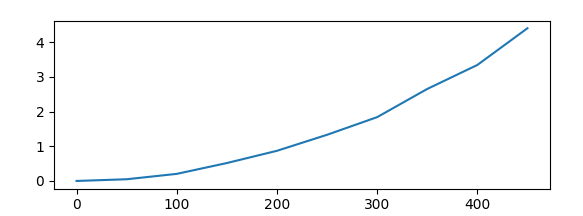
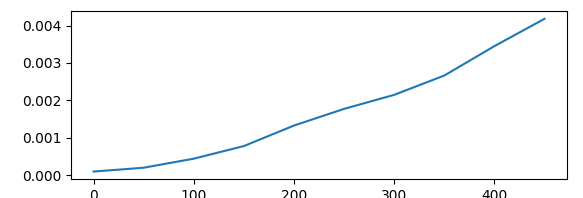
En étudiant ces deux fonctions on remarque que leurs formes générales sont relativement identiques (Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle O(exp(x))}
) mais que la fonction "sorted()" prends un temps bien inférieur à s'exécuter que "triabulle()". On peut donc conclure qu'au point de vue théorique, ces deux formules sont équivalente, mais au point de vue pratique, on va privilégier l'utilisation de "sorted()" car pour la même croissance en fonction de la taille du tableau, elle met beaucoup moins de temps à s'exécuter (ce qui est dû à la compilation de python bien plus efficace sur une fonction déjà incluse dans le langage).
médiane
Comparer la médiane de python à la médiane dite naïve revient a comparer la complexité des deux différents tri. Effectivement les deux fonctions prennent la valeur du milieu sur un tableau trié (grâce aux fonctions de tri vu précédemment) afin de retourner la médiane.
def medianenaive(tab):
'''Entrée: un tableau, Sortie: un entier'''
tri = triabulle(tab)
res= tri[len(tab)//2]
return res
def medianepython(tab):
'''Entrée: un tableau, Sortie: un entier'''
return median(tab)
medianes des medianes, quickselect
L'algorithme de Quickselect est un algorithme permettant de retrouver l'indice nième d’un tableau non trié. Pour cela on prend aléatoirement un élément du tableau et on le compare avec les autres éléments du tableau en créant ainsi deux nouveaux tableaux : les entier supérieurs et les entiers inférieurs à l'élément.
Si l'indice recherché est supérieur ou égal à la taille des inférieurs et est inférieur à la taille du tableau moins la taille des supérieurs alors il s'agit de l'élément.
Sinon, si l'indice est inférieur au tableau des éléments inférieurs on rappel la fonction avec cette fois ci en entrée le tableau des inférieurs et l'indice. Dans le dernier cas, on rappel la fonction avec en entrée le tableau des supérieurs et l'indice moins la taille du tableau auquel on a ajouté la taille des supérieurs.
quickselect :
def quickselectmed(tab):
'''Entrée: un tableau, Sortie: un entier'''
taille = len(tab)
indicemed = taille//2
valmed = cherchevalind(tab,indicemed)
return valmed
def cherchevalind(tab,indice):
elmt = tab[randint(0,len(tab)-1)]
inf = []
sup = []
for i in range(0, len(tab)):
if tab[i] < elmt:
inf.append(tab[i])
elif tab[i]> elmt:
sup.append(tab[i])
if len(tab) - len(sup) > indice >= len(inf):
return elmt
elif len(inf) > indice:
return cherchevalind(inf,indice)
else:
return cherchevalind(sup,indice - len(tab) + len(sup))
L'algorithme de la médiane des médianes est une variante de l'algorithme du quickselect où l'élément aléatoire du tableau est remplacé par la valeur médiane des différentes médianes des paquets de cinq éléments du tableau.
Pour ce faire on sépare le tableau en paquets de cinq éléments. On crée ensuite un nouveau tableau comprenant les médianes des différents paquets. S'il n'y a qu'un élément au sein de ce tableau alors il s'agit de l'élément à appliquer au quickselect. Sinon on recommence l'opération avec ce nouveau tableau.
Médianes des médianes :
def medianemediane(tab):
'''entree tab non trié, sortie int mediane '''
res = 0
medianespaquets = []
nbpaquets = len(tab)//5
for i in range (0, nbpaquets):
paquet = tab[i: i + 5]
medianespaquets.append(mediane(paquet))
if len(tab) % 5 != 0:
paquet = dernierpaquet(tab)
medianespaquets.append(mediane(paquet))
if len(medianespaquets)== 1 :
return medianespaquets[0]
res = medianemediane(medianespaquets)
return res
def medmed(tab):
taille = len(tab)
indicemed = taille//2
return cherchevalindmedmed(tab,indicemed)
def cherchevalindmedmed(tab,indice):
elmt = medianemediane(tab)
inf = []
sup = []
for i in range(0, len(tab)):
if tab[i] < elmt:
inf.append(tab[i])
elif tab[i]> elmt:
sup.append(tab[i])
if len(tab) - len(sup) > indice >= len(inf):
return elmt
elif len(inf) > indice:
return cherchevalind(inf,indice)
else:
return cherchevalind(sup,indice - len(tab) + len(sup))
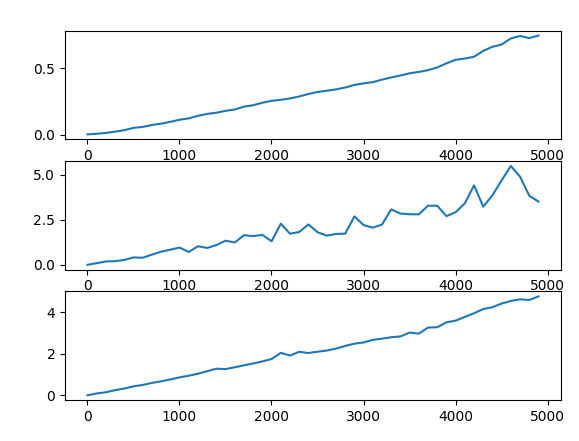
Ces courbes représentent la comparaison de la complexité de la médiane python (en haut), de la médiane des médianes (au milieu) et du quickselect (en bas) afin de retrouver la valeur médiane d'un tableau non trié (sur 1000 essais). On peut voir que la complexité de la médiane des médianes et du quickselect ont une forme linéaire, Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle O(n)}
.
On peut donc en conclure que d'un point de vue théorique les algorithmes de la médiane des médianes et du quick select sont à privilégiés, mais d'un point de vue pratique, la médiane de python prends beaucoup moins de temps à s'exécuter même pour des valeurs de tableaux élevés.
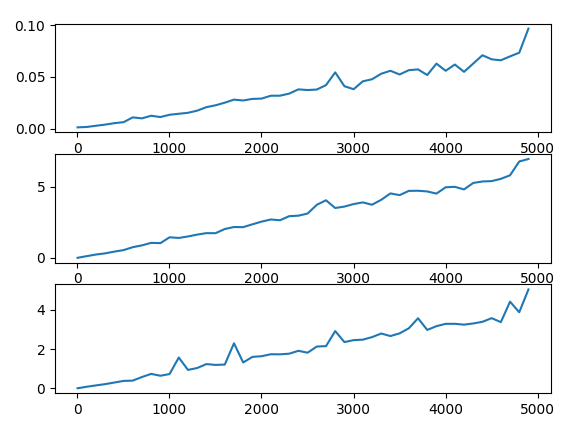
Ces courbes représentent la comparaison de la complexité de la médiane python (en haut), de la médiane des médianes (au milieu) et du quickselect (en bas) afin de retrouver la valeur médiane d'un tableau trié (sur 1000 essais).On remarque que d'un point de vue théorique, que le tableau soit trié ou non trié la complexité reste la même, mais d'un point de vue pratique on remarque que la médiane de python prend beaucoup moins de temps à s'exécuter sur un tableau déjà trié.
Multiplication naive / Karatsuba
L'algorithme de Karatsuba est un algorithme de type "diviser pour mieux régner" permettant de réduire le nombre de calcul lors de la multiplication de grands entiers de même taille.
Dans un premier cas on observe si l'un des deux entiers a une taille de un, c'est à dire est un unique chiffre. Dans ce cas on applique tout simplement la multiplication dite naïve (chaque élément du nombre par le chiffre).
Sinon, on sépare chacun des deux nombres en deux créant quatre nouveaux entiers "a", "b", "c" et "d".
Par exemple pour 1234 * 4567 on crée: a = 12 , b = 34 , c = 45 et d = 67
Ensuite, on peut appliquer deux différents calculs:
-Le calcul dit naïf où on effectue quatre appels récursifs (ac, ad, bc et bd) afin de simplifier le calcul
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle (a * 10^{k} + b)(c*10^{k} + d)}
par:
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle ac * 10^{2k} + (ad + bc) * 10^{k} + bd }
-Le calcul de Karatsuba avec plus que trois appels récursifs (ac, bd et Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle (a-d)*(c-d)}
):
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle ac * 10^{2k} + (ac + bd - (a-b)(c-d))* 10^{k}+ bd}
Multiplication naive:
def multint(T,a):
val = multscalaireT(T,a)
res = 0
for i in range (0,len(val)):
res = res + val[i] * 10 ** (len(val)-1 - i)
return int(res)
def multscalaireT(T,a):
return [T[i] * a for i in range (len(T))]
def multnaive(T1,T2):
res = []
for i in range (len(T1)):
addition =([0] * i) + multscalaireT(T2,T1[i])
res = plus(addition,res)
return res
def plus(T1,T2):
m = min(len(T1),len(T2))
res = [T1[i] + T2[i] for i in range(m)]
res.extend(T1[m:]+T2[m:])
return res
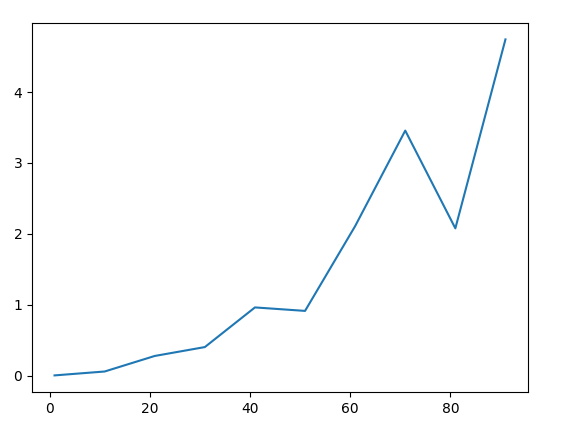
On remarque la complexité de la multiplication naive : Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle (a * 10^{k} + b)(c*10^{k} + d)}
est linéaire.
Karatsuba à quatre appels récursifs:
def karatsubanaive(nb1,nb2):
'''Entrée: deux tableaux, Sortie: un entier'''
taillenb1 = len(nb1)
taillenb2 = len(nb2)
if ( taillenb1 == 1):
return multint(nb2,nb1[0])
elif( taillenb2 == 1) :
return multint(nb1,nb2[0])
return multnaive(nb1,nb2)
else :
mil1=len(nb1)//2
mil2=len(nb2)//2
a=nb1[:mil1]
b=nb1[mil1:]
c=nb2[:mil2]
d=nb2[mil2:]
elmt1 = karatsubanaive(a,c)
elmt2 = karatsubanaive(a,d)
elmt3 = karatsubanaive(b,c)
elmt4 = karatsubanaive(b,d)
return resultatkaratsuban(elmt1,elmt2,elmt3,elmt4,taillenb1)
def resultatkaratsuban(elmt1,elmt2,elmt3,elmt4,taillenb1):
return (elmt1*10**((taillenb1-1)*2)) + ((elmt2 + elmt3) * 10**(taillenb1-1)) + elmt4
La complexité théorique de cet algorithme "karatsuba naïf est la même que la complexité de la multiplication "naïve".
def karatsuba(nb1,nb2):
'''Entrée: deux tableaux, Sortie: un tableau)'''
taillenb1 = len(nb1)
taillenb2 = len(nb2)
if (taillenb1 == 0) or (taillenb1 == 0):
return 0
elif ( taillenb1 == 1):
return multint(nb2,nb1[0])
elif( taillenb2 == 1) :
return multint(nb1,nb2[0])
else :
mil1=len(nb1)//2
mil2=len(nb2)//2
a=nb1[:mil1]
b=nb1[mil1:]
c=nb2[:mil2]
d=nb2[mil2:]
sousab = soustraction(a,b)
souscd = soustraction(c,d)
elmt1 = karatsuba(a,c)
elmt2 = karatsuba(b,d)
elmt3 = karatsuba(sousab,souscd)
return resultatkaratsuba(elmt1,elmt2,elmt3,taillenb1)
def soustraction(tab1,tab2):
nb1 = 0
nb2 = 0
for i in range (0, len(tab1)-1):
nb1 = nb1*10 + tab1[i]
for j in range (0, len(tab2)-1):
nb2 = nb2*10 + tab2[j]
res = nb1 - nb2
tab = []
while res > 0:
reste = res//10
val = res - (reste*10)
tab = tab + [val]
res = reste
return tab
def resultatkaratsuba(elmt1,elmt2,elmt3,taillenb1):
res = (elmt1 * 10**((taillenb1-1)*2)) + (elmt1 + elmt2 - elmt3)*10**(taillenb1-1) + elmt2
return res
On remarque donc que ces trois algorithmes ont une complexité linéaire, mais que la complexité l'algorithme de Karatsuba à trois appels récursifs croît beaucoup moins vite.
CONNETABLE Theo (Tuteur : HYVERNNAT Pierre)