« Utilisateur:Maxent Bernier » : différence entre les versions
| (Une version intermédiaire par le même utilisateur non affichée) | |||
| Ligne 91 : | Ligne 91 : | ||
Il en existe un autre qui utilise les dérivées. |
Il en existe un autre qui utilise les dérivées. |
||
[[Fichier:graphiqueDerivee.png]] |
|||
Les points appartenant au squelette sont les points dont la dérivée est proche de 1. |
|||
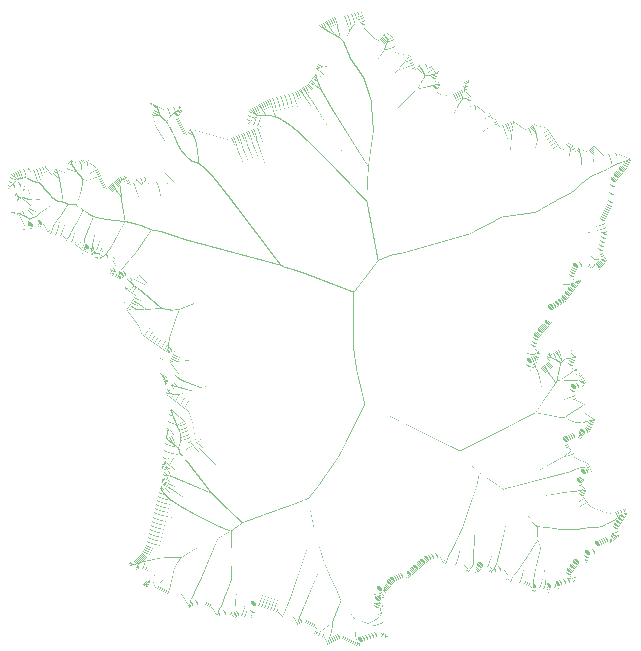
Si on applique cet algorithme à une carte de France (pour avoir une forme quelconque), voici ce que l'on obtient. |
|||
[[Fichier:squeletteBrute.png]] |
|||
On peut voir que la majorité du squelette a été trouvée mais il y a toujours des trous. |
|||
Pour les remplir, on va appliquer le test suivant à chaque point de la forme : |
|||
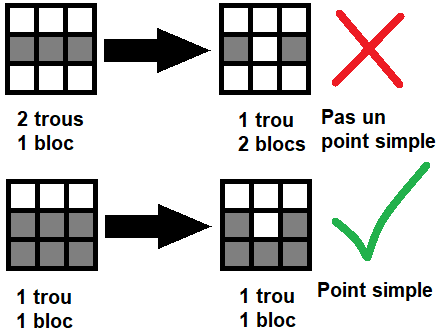
Si retirer le point du milieu de cette grille ne change pas le nombre de blocs (ensembles de points "pleins") et/ou le nombre de trous (ensembles de points "vides"), alors on appelle ce point un "Point Simple", que l'on peut retirer. |
|||
[[Fichier:PointSimple.png]] |
|||
On répète les tests jusqu'à ce qu'il n'y ait plus de changement. |
|||
[[Fichier:Analyse.gif]] |
|||
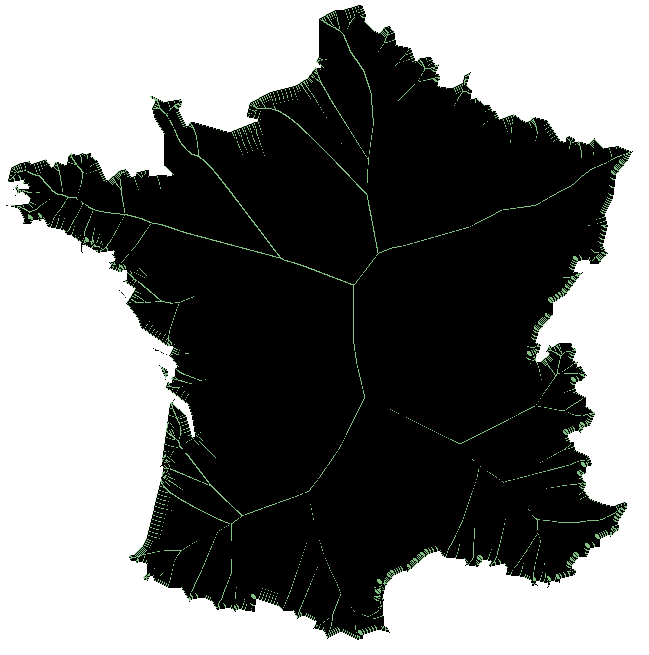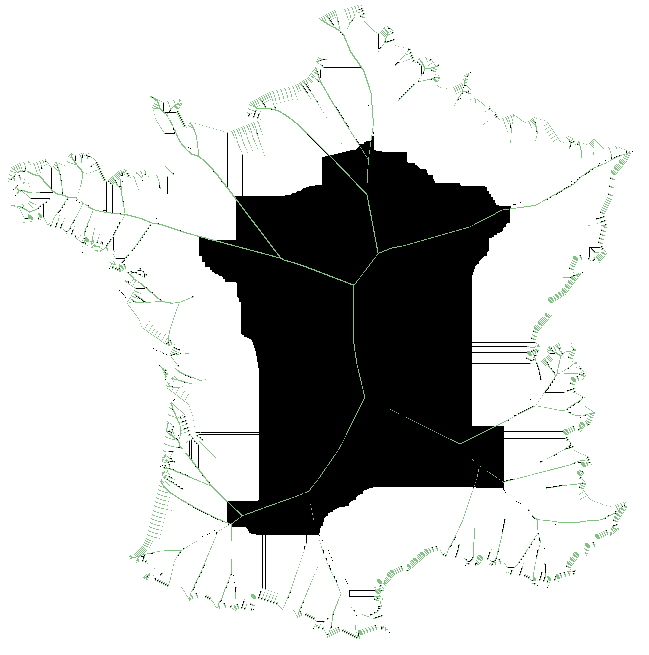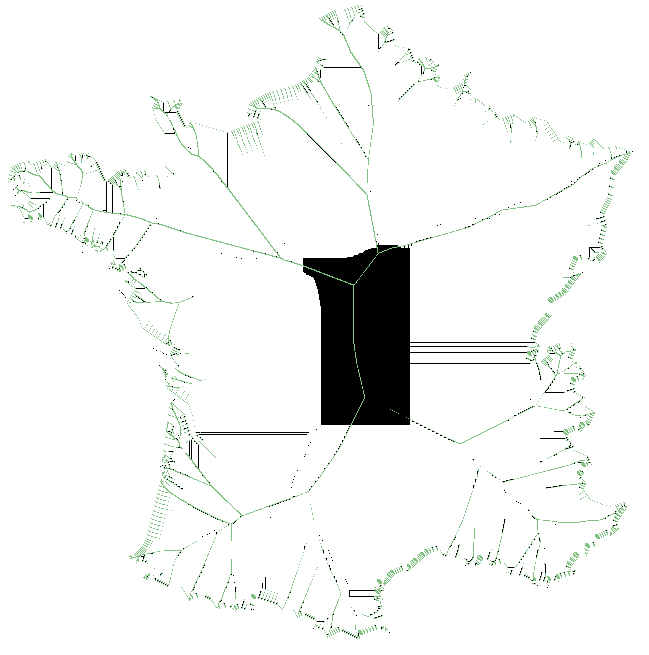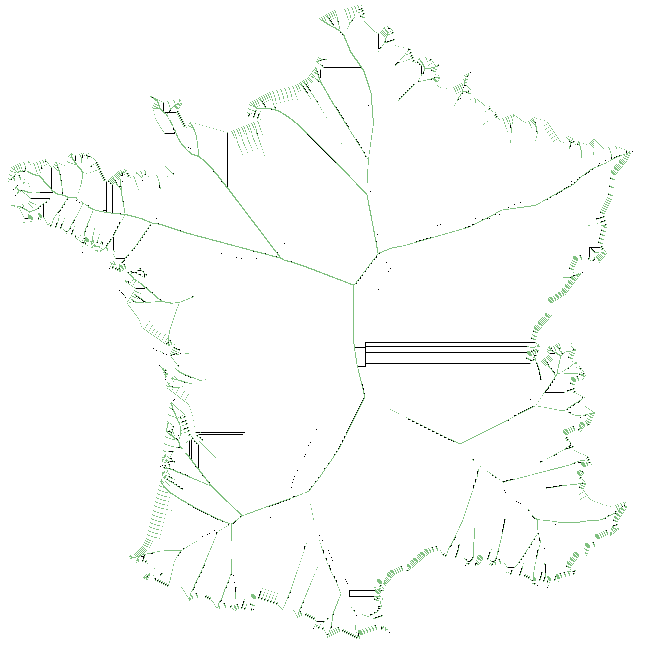
'''/!\''' Bien qu'il y ait des segments du squelette correctement remplis, le code écrit et présenté ci-dessus fait quelques erreurs. |
|||
[[Fichier:Squelette.png]] |
|||
Dernière version du 13 mai 2021 à 14:13
Transformée en distance discrète, diagramme de Voronoi discret, axe médian et squelette
Tuteur : Jacques-Olivier LACHAUD
Etudiant : Maxent BERNIER
Qu'est-ce que Voronoi ?
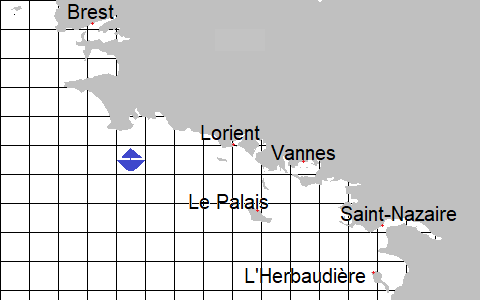
Imaginons un marin en mer. Une tempête s'annonce et il souhaite gagner le port le plus proche. Il dispose d'une carte et connait sa position.
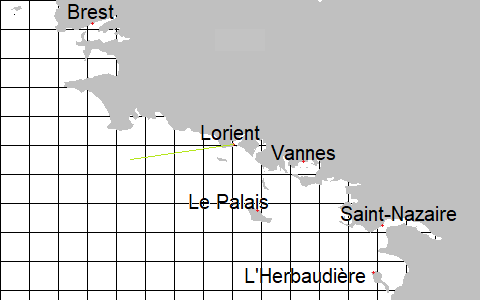
Ici, il est assez simple de voir que le port le plus proche est Lorient. On sait donc que si on se trouve sur cette case, Lorient est toujours le plus proche. Pour le représenter, on peut tracer une ligne ainsi.
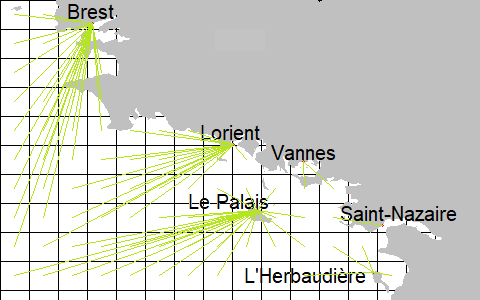
Si on utilise la même logique pour chacune des cases, on obtient ceci :
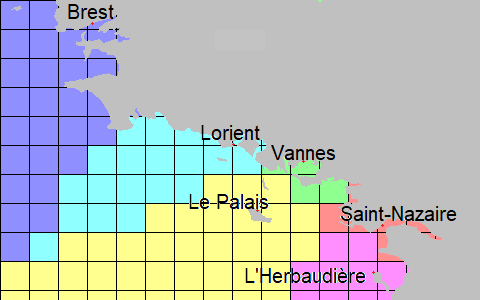
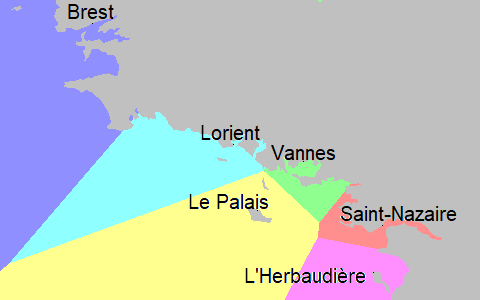
Les lignes n'étant pas très claires, on va les remplacer par des couleurs représentant chaque port.
Nous venons de créer un diagramme de Voronoï; un plan divisé en région en fonction du port (germe) le plus proche. Ici les cases étant très grandes, il est difficile de savoir quelles cases sont dans quelle région. Voici la même carte en traitant chaque pixel de l'image.
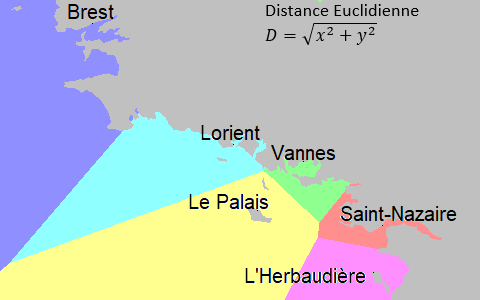
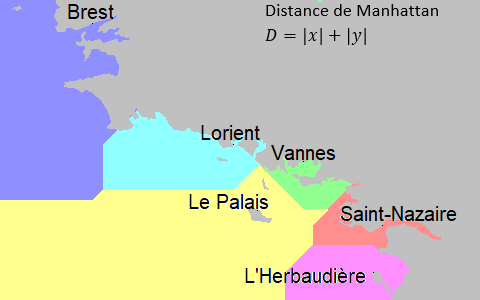
Le mathématicien attentif pourra remarquer que le segment séparant deux régions se trouve sur la médiatrice des ports des deux régions. Ici nous avons utilisé la distance Euclidienne, c'est-à-dire la longueur du segment donc deux points sont les extrémités. Cependant il en existe d'autres. Par exemple, si notre marin ne pouvait se déplacer que horizontalement et verticalement, on utilise alors la distance de Manhattan, qui donne un diagramme différent.
Optimisation d'algorithmes
Un diagramme de Voronoï n'est pas quelque chose de compliqué à programmer, mais il existe de nombreux qui font plus ou moins bien le travail.
L'algorithme le plus intuitif calculerait, pour chaque pixel de l'image, la distance à chaque germe et choisir la plus basse. Si on utilise cet algorithme pour notre exemple précédent, on obtient ce nombre d'opérations :
Cet algorithme a donc un nombre d'opérations égale au produit du nombre de pixels et du nombre de germes. On note donc sa performance O(pn) (avec p le nombre de pixels et n le nombre de germes). Le principal problème d'une telle performance est que si on double de nombre de ports, le nombre d'opération double aussi, ce qui donne des temps de calculs de plus en plus longs.
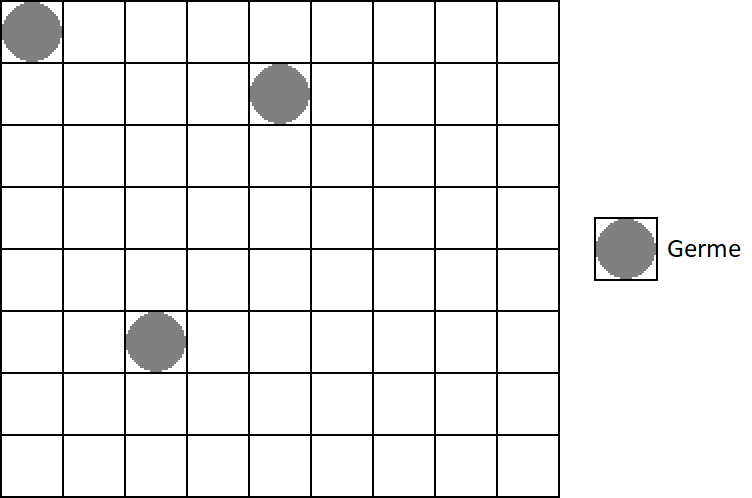
Il existe un algorithme qui évite ce problème, qui cependant perd en simplicité. D'abord on place des germes sur le plan.
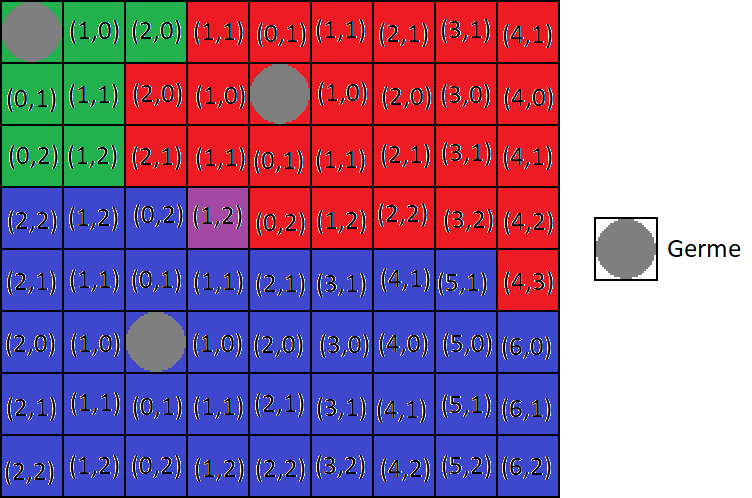
Chaque case va contenir un vecteur qui pointera vers la germe la plus proche. Pour cela, on compare le vecteur de la case de gauche + (1,0) et le vecteur de la case du haut + (0, 1). Par conséquent, les cases de germes ont un vecteur (0, 0).
On remarque cependant que certaines cases pointent une germe qui n'est pas leur plus proche. Pour réparer cela, on effectue trois autres balayages de la grille, respectivement :
- Démarre en haut à droite vers le bas gauche, vérifie la case supérieure et à droite - Démarre en bas à gauche vers le haut droite, vérifie la case inférieure et à gauche - Démarre en bas à droite vers le haut gauche, vérifie la case inférieure et à droite
Après quoi on obtient une grille de vecteurs correctement orientés vers la germe la plus proche.
Puis on attribue la germe la plus proche.
Si on revient sur la notion de performance, voici ce que l'on obtient pour cet algorithme :
Ce nouvel algorithme est non seulement plus performant que l'ancien, il prendra le même nombre d'opérations qu'il y ait une germe ou des centaines. On note sa performance O(p) (et non O(4p) car la notation O() ne prend en compte que les variables, pas les constantes).
Squelette Topologique
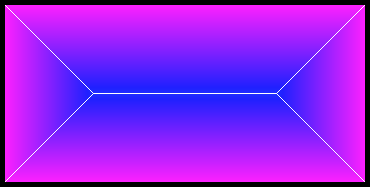
On peut découvrir quelque chose d'intéressant en simulant beaucoup de germes, comme sur une forme par exemple. Ci-dessous, on a coloré chaque pixel en fonction de sa distance à un pixel noir.
On peut distinguer des segments dans les couleurs, mis en évidence ci-dessous.
Ces segments forment le squelette topologique de la forme, une version plus fine de la forme originale qui est équidistante aux bordures de la forme.
Pour l'isoler, il faut savoir de quoi est composé le squelette : il s'agit de l'ensemble des points locaux les plus distants aux germes. Un algorithme intuitif serait alors de noter les points dont la distance à une germe est plus grande que celles de leurs voisins.
Cependant, cet algorithme ne marche que pour les formes basiques comme les rectangles, sinon le squelette est incomplet.
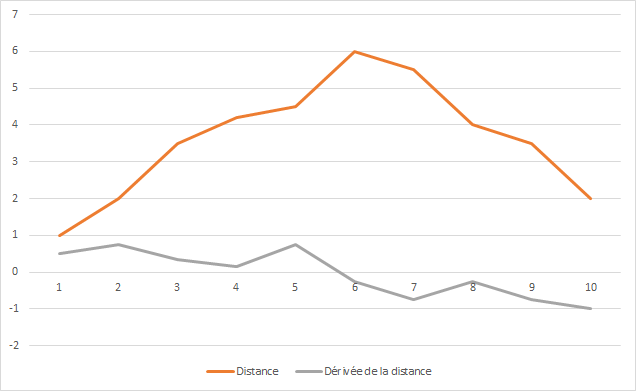
Il en existe un autre qui utilise les dérivées.
Les points appartenant au squelette sont les points dont la dérivée est proche de 1. Si on applique cet algorithme à une carte de France (pour avoir une forme quelconque), voici ce que l'on obtient.
On peut voir que la majorité du squelette a été trouvée mais il y a toujours des trous. Pour les remplir, on va appliquer le test suivant à chaque point de la forme :
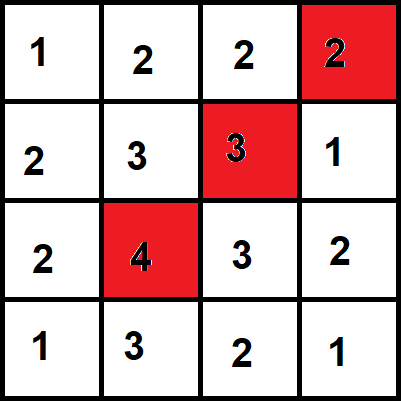
Si retirer le point du milieu de cette grille ne change pas le nombre de blocs (ensembles de points "pleins") et/ou le nombre de trous (ensembles de points "vides"), alors on appelle ce point un "Point Simple", que l'on peut retirer.
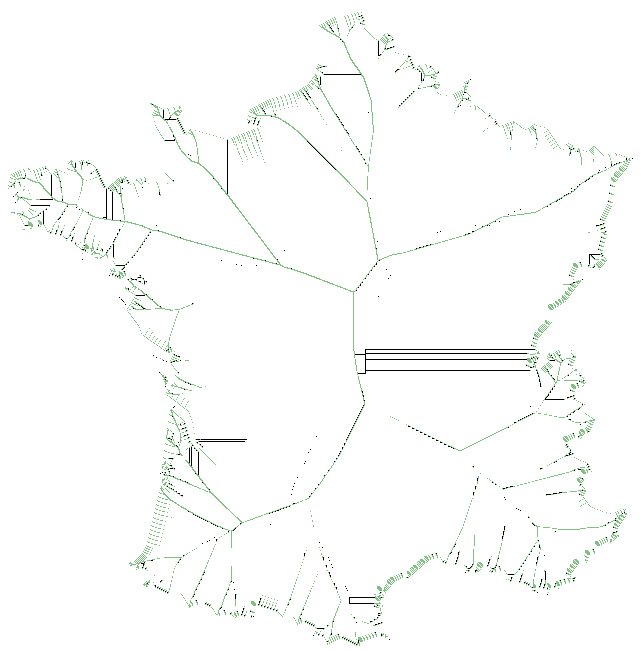
On répète les tests jusqu'à ce qu'il n'y ait plus de changement.
/!\ Bien qu'il y ait des segments du squelette correctement remplis, le code écrit et présenté ci-dessus fait quelques erreurs.