« Machines de Turing » : différence entre les versions
Aucun résumé des modifications |
|||
| (40 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
Machine de Turing |
== '''Machine de Turing''' == |
||
Machine de Turing : |
|||
La machine de Turing à été inventée par Alan Turing en 1936. |
La machine de Turing à été inventée par Alan Turing en 1936. |
||
Elle représente le fonctionnement d’un appareil mécanique de calcul comme par exemple un ordinateur, c’est ce qui a donner une idée précise du concept de l’algorithme |
Elle représente le fonctionnement d’un appareil mécanique de calcul comme par exemple un ordinateur, c’est ce qui a donner une idée précise du concept de l’algorithme |
||
Le concept de Machine de Turing a été inventé avant l’ordinateur. Elle devait représenter une personne virtuelle qui devait exécuter une procédure définie par l’utilisateur qui consiste à changer le contenu des cases d’un ruban infini, et en choisissant ce contenu parmi un ensemble fini de symbole. |
Le concept de Machine de Turing a été inventé avant l’ordinateur. Elle devait représenter une personne virtuelle qui devait exécuter une procédure définie par l’utilisateur qui consiste à changer le contenu des cases d’un ruban infini, et en choisissant ce contenu parmi un ensemble fini de symbole. |
||
== '''Définition''' == |
|||
Un problème = une solution |
|||
Définition : |
|||
La machine de Turing est composée: |
La machine de Turing est composée: |
||
\begin{itemize} |
|||
\item d' un ruban infini à droite et à gauche sur lequel il y a des cases, chaque case peut contenir des symboles. Si il n’y a pas de symboles, c’est des cases blanches |
|||
\item d’une tête de lecture / écriture : lit et écrit les symboles sur le rubans puis se déplace à droite ou à gauche selon la procédure |
|||
\item un registre d’état : c’est un registre mémorise l’état dans lequel il se trouve, il existe un spécial, c’est l’état de départ qui initialise la machine avant l'exécution de celle ci |
|||
\item Table d’action : la table indique à la machine quel symbole écrire et comment se déplacer la tête de lecture et elle dit aussi le nouvel état à exécuter. Si il n’y a plus d’action à faire, la machine s’arrête. |
|||
\end{itemize} |
|||
- D' un ruban infini à droite et à gauche sur lequel il y a des cases, chaque case peut contenir des symboles. Si il n’y a pas de symboles, c’est des cases blanches |
|||
Exemple: |
|||
- D’une tête de lecture / écriture : lit et écrit les symboles sur le rubans puis se déplace à droite ou à gauche selon la procédure |
|||
La machine de Turing à pour symbole {‘0’,’1’} et un autre qui correspond au symbole de la case vide. Nous avons en entrée de cette machine une suite de 1 et de 0. La tête de lecture/écriture se trouve à gauche de la suite de nombre |
|||
En exemple on va ajouter 1 à un nombre binaire. Pour cette fonction il nous faut 3 états. |
|||
- Un registre d’état : c’est un registre mémorise l’état dans lequel il se trouve, il existe un spécial, c’est l’état de départ qui initialise la machine avant l'exécution de celle ci |
|||
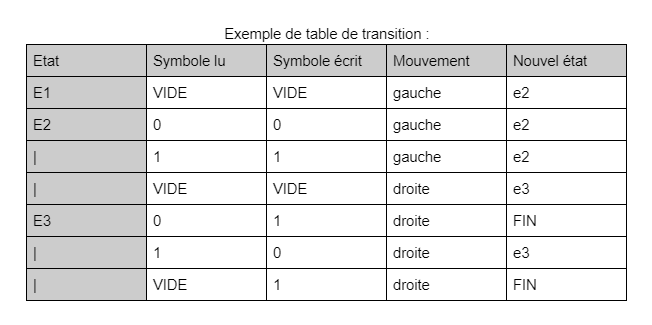
Exemple de table de transition : |
|||
Etat |
|||
Symbole lu |
|||
Symbole écrit |
|||
Mouvement |
|||
Nouvel état |
|||
E1 |
|||
VIDE |
|||
VIDE |
|||
gauche |
|||
e2 |
|||
E2 |
|||
0 |
|||
0 |
|||
gauche |
|||
e2 |
|||
| |
|||
1 |
|||
1 |
|||
gauche |
|||
e2 |
|||
| |
|||
VIDE |
|||
VIDE |
|||
droite |
|||
e3 |
|||
E3 |
|||
0 |
|||
1 |
|||
droite |
|||
FIN |
|||
| |
|||
1 |
|||
0 |
|||
droite |
|||
e3 |
|||
| |
|||
VIDE |
|||
1 |
|||
droite |
|||
FIN |
|||
- Table d’action : la table indique à la machine quel symbole écrire et comment se déplacer la tête de lecture et elle dit aussi le nouvel état à exécuter. Si il n’y a plus d’action à faire, la machine s’arrête. |
|||
== '''Exemple''' == |
|||
La machine de Turing à pour symbole {‘0’,’1’} et un autre qui correspond au symbole de la case vide. Nous avons en entrée de cette machine une suite de 1 et de 0. La tête de lecture/écriture se trouve à gauche de la suite de nombre |
|||
[[Fichier:schema.jpg]] |
|||
Exemple pour ajouter 1 au nombre : { 10101 } |
|||
En exemple on va ajouter 1 à un nombre binaire. Pour cette fonction il nous faut 3 états. |
|||
Etape |
|||
Etat |
|||
Ruban |
|||
[[Fichier:tableau_etat1.png]] |
|||
Exemple pour ajouter 1 au nombre : { 10101 } |
|||
Etape |
|||
Etat |
|||
Ruban |
|||
Etape |
|||
Etat |
|||
Ruban |
|||
1 |
|||
e1 |
|||
_10101 |
|||
4 |
|||
e2 |
|||
10101 |
|||
7 |
|||
e2 |
|||
10101_ |
|||
2 |
|||
e2 |
|||
10101 |
|||
5 |
|||
e2 |
|||
10101 |
|||
8 |
|||
e3 |
|||
10100 |
|||
3 |
|||
e2 |
|||
10101 |
|||
6 |
|||
e2 |
|||
10101 |
|||
9 |
|||
e3 |
|||
10110 FIN |
|||
La machine commence par l’état 1, qui lit le symbole VIDE (une case blanche) puis le remplace par le symbole VIDE puis se déplace à gauche. |
|||
Elle passe à l’état 2, elle remplace le symbole lu par le même symbole et se déplace à gauche et quand se retrouve tout à droite du nombre et rencontre un symbole VIDE elle écrit VIDE et se déplace à droite |
|||
Elle passe à l’état 3, quand elle lit un symbole 0 elle écrit 1 puis se déplace à droite et c’est la FIN du programme, quand elle lit un symbole 1 elle écrit 0 puis se déplace à droite et quand elle lit le symbole VIDE elle écrit 1 puis se déplace à droite et c’est la FIN du programme. |
|||
Machine de Turing universelle : |
|||
La machine de Turing universelle est une machine qui peut faire n’importe quel calculs, tout ce qui est calculable, n’importe quelle fonction récursive et peut analyser n’importe quel langage récursive |
|||
[[Fichier:exemple1.jpg]] |
|||
La machine commence par '''l’état 1''', qui lit le symbole '''VIDE''' (une case blanche) puis le remplace par le symbole VIDE puis se déplace à '''gauche'''. |
|||
Elle passe à '''l’état 2''', elle remplace le symbole lu par le même symbole et se déplace à '''gauche''' et quand se retrouve tout à droite du nombre et rencontre un symbole '''VIDE''' elle écrit '''VIDE''' et se déplace à '''droite''' . |
|||
Elle passe à '''l’état 3''', quand elle lit un symbole '''0''' elle écrit '''1''' puis se déplace à '''droite''' et c’est la '''FIN''' du programme, quand elle lit un symbole '''1''' elle écrit '''0''' puis se déplace à '''droite''' et quand elle lit le symbole '''VIDE''' elle écrit '''1''' puis se déplace à '''droite''' et c’est la '''FIN''' du programme. |
|||
Machine de Turing non-déterministe : |
|||
Le but d’une machine de Turing non déterministe c’est pour chaque point c’est faire un choix, elle peut exécuter au moins 2 transitions différentes à un endroit. |
|||
Voici quelques exemples de machine de Turing en python |
|||
↓ ↷ |
|||
a . |
|||
q0 q1 |
|||
Ajouter 1 : [[Fichier:ajouter_1_turing_v2.txt]] |
|||
soit elle peut exécuter q0 2x |
|||
soit elle peut exécuter q1 |
|||
Soustraire 1 : [[Fichier:soustraire_1.txt]] |
|||
Multiplier par 2 : [[Fichier:multiplier_par_2.txt]] |
|||
ex : |
|||
Le langage sur {a,b} des mots dont la 6ème lettre en partant de la fin est un a est-il régulier ? |
|||
== '''Machine de Turing universelle ''' == |
|||
a,b |
|||
⟳ a a,b a,b a,b a,b a,b |
|||
→ O → O → O → O → O → O → O |
|||
6e 5e 4e 3e 2nd 1er |
|||
Le langage est régulier |
|||
Il existe un automate déterministe le reconnaissant avec au plus 128 états (automates minimal en à 64) |
|||
Machine de Turing Non-déterministe permettent de façon simple de donner des indications sur la complexité déterministe d’un problème ou comment l’aborder efficacement |
|||
La machine de Turing universelle est une machine qui prend en paramètre une autre machine de Turing, ce qui nous permet de faire n’importe quel calculs. |
|||
Def : Une machine de Turing non déterministe décide un langage L, si tout : |
|||
Grâce à la machine de Turing universelle, l'ordinateur peut éditer n'importe quel programme. |
|||
il n’y a aucun calcul infini |
|||
Un mot est dans L si et seulement s’il existe un calcul pour ce mot passant par une configuration finale |
|||
Voici un programme qui représente une machine de Turing universelle.[[Fichier:machine_universelle.txt]] |
|||
Une machine de Turing non déterministe est utile pour optimiser, transport routier, ordonnancement de tâche, gestion d’usine… C’est un outil théorique et qui donne beaucoup d'informations sur la nature du problème et sur comment l’aborder mais ne résout pas le problème. |
|||
Dernière version du 25 mai 2022 à 09:54
Machine de Turing
La machine de Turing à été inventée par Alan Turing en 1936. Elle représente le fonctionnement d’un appareil mécanique de calcul comme par exemple un ordinateur, c’est ce qui a donner une idée précise du concept de l’algorithme Le concept de Machine de Turing a été inventé avant l’ordinateur. Elle devait représenter une personne virtuelle qui devait exécuter une procédure définie par l’utilisateur qui consiste à changer le contenu des cases d’un ruban infini, et en choisissant ce contenu parmi un ensemble fini de symbole.
Définition
La machine de Turing est composée:
- D' un ruban infini à droite et à gauche sur lequel il y a des cases, chaque case peut contenir des symboles. Si il n’y a pas de symboles, c’est des cases blanches
- D’une tête de lecture / écriture : lit et écrit les symboles sur le rubans puis se déplace à droite ou à gauche selon la procédure
- Un registre d’état : c’est un registre mémorise l’état dans lequel il se trouve, il existe un spécial, c’est l’état de départ qui initialise la machine avant l'exécution de celle ci
- Table d’action : la table indique à la machine quel symbole écrire et comment se déplacer la tête de lecture et elle dit aussi le nouvel état à exécuter. Si il n’y a plus d’action à faire, la machine s’arrête.
Exemple
La machine de Turing à pour symbole {‘0’,’1’} et un autre qui correspond au symbole de la case vide. Nous avons en entrée de cette machine une suite de 1 et de 0. La tête de lecture/écriture se trouve à gauche de la suite de nombre
En exemple on va ajouter 1 à un nombre binaire. Pour cette fonction il nous faut 3 états.
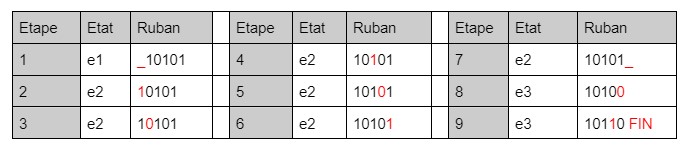
Exemple pour ajouter 1 au nombre : { 10101 }
La machine commence par l’état 1, qui lit le symbole VIDE (une case blanche) puis le remplace par le symbole VIDE puis se déplace à gauche.
Elle passe à l’état 2, elle remplace le symbole lu par le même symbole et se déplace à gauche et quand se retrouve tout à droite du nombre et rencontre un symbole VIDE elle écrit VIDE et se déplace à droite .
Elle passe à l’état 3, quand elle lit un symbole 0 elle écrit 1 puis se déplace à droite et c’est la FIN du programme, quand elle lit un symbole 1 elle écrit 0 puis se déplace à droite et quand elle lit le symbole VIDE elle écrit 1 puis se déplace à droite et c’est la FIN du programme.
Voici quelques exemples de machine de Turing en python
Ajouter 1 : Fichier:Ajouter 1 turing v2.txt
Soustraire 1 : Fichier:Soustraire 1.txt
Multiplier par 2 : Fichier:Multiplier par 2.txt
Machine de Turing universelle
La machine de Turing universelle est une machine qui prend en paramètre une autre machine de Turing, ce qui nous permet de faire n’importe quel calculs. Grâce à la machine de Turing universelle, l'ordinateur peut éditer n'importe quel programme.
Voici un programme qui représente une machine de Turing universelle.Fichier:Machine universelle.txt