« Stéganographie "BPC" » : différence entre les versions
| (27 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 2 : | Ligne 2 : | ||
Elève : Hania Boudjaj |
Elève : Hania Boudjaj |
||
==Introduction== |
|||
==Présentation du projet== |
|||
Nous pouvons définir la stéganographie comme suit :<br> |
|||
"Ensemble de techniques permettant de transmettre une information en la dissimulant au sein d'une autre information (photo, vidéo, texte, etc.) sans rapport avec la première et le plus souvent anodine, essentiellement à l'aide de logiciels spécialisés."<br> |
|||
On attribue la première mention de la stéganographie telle que définie ci-dessus à l'historien grec Hérodote. Il décrit dans son ouvrage Historia, une tablette de bois gravée qu’on recouvre de cire de sorte à cacher un message.<br> |
|||
==Histoire== |
|||
(du grec steganos, caché, et graphein, écrire)<br> |
|||
Ensemble de techniques permettant de transmettre une information en la dissimulant au sein d'une autre information (photo, vidéo, texte, etc.) sans rapport avec la première et le plus souvent anodine, essentiellement à l'aide de logiciels spécialisés.<br> |
|||
On attribue la première mention de la stéganographie telle que définie plus tôt à l'historien grec Hérodote. Il décrit dans son ouvrage Historia, une tablette de bois gravée qu’on recouvre de cire.<br> |
|||
Dans le cadre de ce projet, nous nous intéresserons à des algorithmes de stéganographie qui permettent de cacher du texte dans une image.<br> |
Dans le cadre de ce projet, nous nous intéresserons à des algorithmes de stéganographie qui permettent de cacher du texte dans une image.<br> |
||
De plus, nous ne considérons pas les formats d'image avec compression. |
|||
==La stéganographie LSB== |
==La stéganographie LSB== |
||
===Principe de base=== |
===Principe de base=== |
||
Dans un premier temps, décomposons l'organisation d'une image : <br> |
|||
Une image est composée de pixels eux-même composés de trois octets. Chacun de ces octets correspond à une composante couleur du pixel, Red, Green et Blue. |
|||
Une image est composée de pixels eux-mêmes composés de trois octets. Chacun de ces octets correspond à une composante couleur du pixel, Red, Green et Blue. |
|||
Chaque composante peut prendre une valeur allant de 0 à 255.<br> |
Chaque composante peut prendre une valeur allant de 0 à 255.<br> |
||
[[Fichier:Image_decomp_lsb.PNG|La décomposition d'une image.]]<br> |
|||
Ainsi, on peut modifier les n bits de poids faible d’un octet sans que cela soit visible à l'œil nu. Notons cependant que plus le poids du bit modifié augmente, plus la modification sera visible.<br> |
Ainsi, on peut modifier les n bits de poids faible d’un octet sans que cela soit visible à l'œil nu. Notons cependant que plus le poids du bit modifié augmente, plus la modification sera visible.<br> |
||
La stéganographie LSB permet donc de remplacer les n bits de poids faible des pixels d’une image par les bits d’une chaîne de caractère. On peut alors cacher un message dans une image.<br> |
La stéganographie LSB permet donc de remplacer les n bits de poids faible des pixels d’une image par les bits d’une chaîne de caractère. On peut alors cacher un message dans une image.<br> |
||
Dans le cadre de ce projet, nous utiliserons la bibliothèque Pillow qui permet de manipuler facilement des images. |
|||
===Exemples=== |
===Exemples=== |
||
<table> |
|||
===Problèmes=== |
|||
<tr> |
|||
Plus la taille du message à cacher est importante, plus le nombre de bit nécessaire à l’encodage augmente.<br> |
|||
<td>[[Fichier:Chablais-orig.png|200px|frameless|left|Image originale.]]</td> |
|||
Or, comme mentionné plus tôt, plus le poids du bit modifié augmente, plus la modification sera visible.<br> |
|||
<td>[[Fichier:LSB1.png |200px|frameless|left|Image modifiée sur 1 bit de poids faible.]]</td> |
|||
</tr> |
|||
<tr> |
|||
<td>''Image originale.''</td> |
|||
<td>''Image modifiée sur 1 bit<br>de poids faible.''</td> |
|||
</tr> |
|||
</table> |
|||
===Code=== |
|||
<code> |
|||
from PIL import Image |
|||
def cache(img_name: str, msg: str, nom_img_fin: str, nb_bits: int = 1, ): |
|||
if not (1 <= nb_bits <= 8): |
|||
print("Le nombre de bits par couleur doit être entre 1 et 8.") |
|||
return |
|||
# Ouvrir et convertir l'image en mode RGB : |
|||
image_ori = Image.open(img_name) |
|||
image_rgb = image_ori.convert("RGB") # Evite les problèmes liés à la transparence. |
|||
data_bytes = bytearray(image_rgb.tobytes()) |
|||
# Encodage du message en binaire. |
|||
msg_bin = "".join((f"{ord(c):08b}") for c in msg ) |
|||
msg_len = len(msg_bin) |
|||
msg_len_bin = f"{msg_len:016b}" # 16 bits pour représenter la taille du message |
|||
message_complet = msg_len_bin + msg_bin |
|||
# Vérification de la capacité |
|||
capacite = len(data_bytes) * nb_bits |
|||
if len(message_complet) > capacite: |
|||
print(f"Le message est trop long pour être encodé dans cette image avec {str(nb_bits)} bit(s) par couleur.") |
|||
return |
|||
# Encodage dans le bytearray. |
|||
bit_index = 0 |
|||
for i in range(len(data_bytes)): |
|||
byte = data_bytes[i] |
|||
for b in range(nb_bits): |
|||
if bit_index >= len(message_complet): |
|||
break |
|||
# Remplacer les bits les moins significatifs |
|||
message_bit = int(message_complet[bit_index]) |
|||
bit_index += 1 |
|||
byte &= ~(1 << b) |
|||
byte |= (message_bit << b) |
|||
data_bytes[i] = byte |
|||
if bit_index >= len(message_complet): |
|||
break |
|||
# Reconstruction de l'image. |
|||
img_fin = Image.frombytes("RGB", image_rgb.size, bytes(data_bytes)) |
|||
img_fin.save(nom_img_fin) |
|||
print(f"Message encodé avec succès dans {nom_img_fin}avec {str(nb_bits)} bit(s) par couleur.") |
|||
def discover(img_name: str, nb_bits: int = 1): |
|||
if not (1 <= nb_bits <= 8): |
|||
print("Le nombre de bits par couleur doit être entre 1 et 8.") |
|||
return |
|||
# Ouvrir l'image. |
|||
image_ori = Image.open(img_name) |
|||
image_rgb = image_ori.convert("RGB") |
|||
data_bytes = bytearray(image_rgb.tobytes()) |
|||
bits_lus = "" |
|||
taille_msg = None |
|||
valeur = 0 |
|||
for byte in data_bytes: |
|||
for b in range(nb_bits): |
|||
bit = (byte >> b) & 1 |
|||
bits_lus += str(bit) |
|||
# Lecture des 16 premiers bits, qui contiennent la taille. |
|||
if len(bits_lus) == 16 and taille_msg is None: |
|||
for i in range(16): |
|||
valeur = (valeur << 1) | (1 if bits_lus[i] == '1' else 0) |
|||
taille_msg = valeur |
|||
total_bits = 16 + taille_msg |
|||
if taille_msg is not None and len(bits_lus) >= total_bits: |
|||
break |
|||
if taille_msg is not None and len(bits_lus) >= total_bits: |
|||
break |
|||
# Reconstruction du message. |
|||
message_bits = bits_lus[16:16 + taille_msg] |
|||
octets = [message_bits[i:i+8] for i in range(0, len(message_bits), 8)] |
|||
message = "".join(chr(int(o, 2)) for o in octets) |
|||
print(f"MESSAGE DÉCODÉ : {message}") |
|||
return message |
|||
</code> |
|||
===Problème=== |
|||
Plus la taille du message à cacher est importante, plus le nombre de bits nécessaires à l’encodage augmente.<br> |
|||
<table> |
|||
<tr> |
|||
<td>[[Fichier:LSB4.png |200px|frameless|left|Image modifiée sur 4 bits de poids faible.]]</td> |
|||
</tr> |
|||
<tr> |
|||
<td>''Image modifiée sur 4 bits<br>de poids faible.''</td> |
|||
</tr> |
|||
</table> |
|||
Or, comme mentionné plus tôt, plus le poids du bit modifié augmente, plus l'altération sera visible.<br> |
|||
Pour remédier à ce problème, nous pouvons nous tourner vers la Stéganographie BPC. |
Pour remédier à ce problème, nous pouvons nous tourner vers la Stéganographie BPC. |
||
==La stéganographie BPC== |
==La stéganographie BPC== |
||
===Principe de base=== |
===Principe de base=== |
||
Contrairement à la stéganographie LSB, nous allons maintenant choisir dans quelles parties de l’image cacher notre message. Pour cela, nous allons nous intéresser à la complexité d’une image |
Contrairement à la stéganographie LSB, nous allons maintenant choisir dans quelles parties de l’image cacher notre message. Pour cela, nous allons nous intéresser à la complexité d’une image :<br> |
||
Soit une image composée de pixels RGB. Nous allons diviser cette image en blocs de 8*8 pixels. |
|||
<table> |
|||
<tr> |
|||
<td>[[Fichier:Bcp_decomp.PNG|frameless|left|La nouvelle décomposition de l'image.]]</td> |
|||
</tr> |
|||
</table> |
|||
Pour décider si oui ou non nous cachons une partie du message dans le bloc actuel, nous allons calculer sa complexité.<br> |
|||
Pour cela, il suffit de compter le nombre de changements entre deux bits consécutifs pour chaque ligne et chaque colonne du bloc. |
|||
<table> |
|||
<tr> |
|||
<td>[[Fichier:Bpc_bloc.PNG|frameless|left|La décomposition d'un bloc.]]</td> |
|||
</tr> |
|||
</table> |
|||
Plus le nombre de changements est élevé dans un bloc, plus il est complexe. Nous fixerons un seuil de complexité arbitraire. Si le nombre de changements est supérieur à ce seuil, le bloc est complexe. Sinon, il est simple.<br> |
|||
Intervient alors un nouveau problème : lorsqu’on encode une partie du message, il y est possible que le bloc change soudainement de complexité (si, dû aux changements effectués sur les bits, le nombre de changement diminue), ce qui pose problème pour le décodage.<br> |
|||
Pour y remédier, nous effectuons l’opération arithmétique XOR entre le bloc et un damier :<br> |
|||
Un damier de 8*8 pixels correspond simplement à une suite de pixels noirs et pixels blancs. On peut ainsi le représenter par une succession de 3 canaux RGB fixés à 0 suivis de 3 canaux RGB fixés à F (en base 16).<br> |
|||
<table> |
|||
<tr> |
|||
<td>[[Fichier:Bpc_damier.PNG|frameless|left|Représentation visuelle du damier.]]</td> |
|||
</tr> |
|||
</table> |
|||
On obtient alors deux suites d'octets de même longueur qu'on peut "XOR" l'une avec l'autre.<br> |
|||
Cette méthode permet de faire passer la complexité d’un bloc de simple à complexe. Elle est donc appliquée sur tous les blocs qui étaient classés comme "complexe", et dans lesquels on à caché une partie du message, qui sont ensuite passés à "simple". |
|||
Soit une image composée de pixel RGB. Nous allons diviser cette image en blocs de 8*8 pixels. Pour décider si oui ou non nous cachons une partie du message dans le bloc actuel, nous allons calculer sa complexité. |
|||
Pour cela, il suffit de compter le nombre de changement entre deux bits consécutifs en ligne et en colonnes? Plus le nombre de changements est élevé dans un bloc, plus il est complexe. |
|||
Intervient alors un nouveau problème : lorsqu’on encode une partie du message, il y est possible que le bloc change soudainement de complexité, ce qui pose problème pour le décodage. |
|||
Pour y remédier, nous effectuons l’opération arithmétique XOR entre le bloc et un damier. Cette méthode permet de faire passer la complexité d’un bloc de simple à complexe. |
|||
===Exemples=== |
===Exemples=== |
||
<table> |
|||
<tr> |
|||
<td>[[Fichier:Chablais-orig.png|200px|frameless|left|Image originale.]]</td> |
|||
<td>[[Fichier:BPC1.png |200px|frameless|left|Image modifiée sur 1 bit de poids faible.]]</td> |
|||
<td>[[Fichier:BPC4.png |200px|frameless|left|Image modifiée sur 4 bits de poids faible.]]</td> |
|||
<td>[[Fichier:BPC8.png |200px|frameless|left|Image modifiée sur 8 bits.]]</td> |
|||
</tr> |
|||
<tr> |
|||
<td>''Image originale.''</td> |
|||
<td>''Image modifiée sur 1 bit<br>de poids faible.''</td> |
|||
<td>''Image modifiée sur 4 bits<br>de poids faible.''</td> |
|||
<td>''Image modifiée sur 8 bits.''</td> |
|||
</tr> |
|||
</table> |
|||
===Code=== |
===Code=== |
||
<code> |
|||
from PIL import Image |
|||
def complexite(bloc_pixels): |
|||
""" |
|||
Une fonction qui permet de calculer la complexité d'un bloc de 8*8 pixels. |
|||
Entrée : Un tableau qui contient les pixels du bloc actuel. |
|||
Sortie : int, un compteur qui indique le nombre de changements de bits consécutifs. |
|||
""" |
|||
changement = 0 |
|||
# On regarde la complexité des colonnes (pixels de même x) : |
|||
for x in range(len(bloc_pixels[0])): |
|||
for couleur in range(3): # Pour chaque composante RGB |
|||
for bit_pos in range(8): # Pour chaque position de bit (de 0 à 7) |
|||
prev_bit = None # Parce qu'au début il n'y a pas de bit précédent |
|||
for y in range(len(bloc_pixels)): |
|||
if bloc_pixels[y][x] is None: |
|||
continue |
|||
bit = (bloc_pixels[y][x][couleur] >> bit_pos) & 1 # On extrait le bit spécifique de la composante couleur RGB |
|||
if prev_bit is not None and bit != prev_bit: # On regarde s'il y a un chagement entre deux bits consécutifs |
|||
changement += 1 |
|||
prev_bit = bit |
|||
# On regarde la complexité des lignes (pixels de même y) : |
|||
for y in range(len(bloc_pixels)): |
|||
for couleur in range(3): |
|||
for bit_pos in range(8): |
|||
prev_bit = None |
|||
for x in range(len(bloc_pixels[0])): |
|||
if bloc_pixels[y][x] is None: |
|||
continue |
|||
bit = (bloc_pixels[y][x][couleur] >> bit_pos) & 1 |
|||
if prev_bit is not None and bit != prev_bit: |
|||
changement += 1 |
|||
prev_bit = bit |
|||
return changement |
|||
def bpc(img_name: str, msg: str, nom_img_fin: str = "BPC8bis2.png", damier_name: str = "damier.png", nb_bits: int = 1, seuil_complexite: int = 500): |
|||
""" |
|||
Une fonction qui permet de caché un message dans une image en fonction de la complexité de blocs 8*8 pixels. |
|||
Entrées : |
|||
-img_name : Nom de l'image d'origine |
|||
-msg : message à caché |
|||
-nom_img_fin : nom de l'image qui contient le message caché |
|||
-damier_name : nom de l'image qui contient le damier |
|||
-nb_bits : nombre de bits sur lesquels on encode le message |
|||
Sortie : img_fin, une image qui contient un message. |
|||
""" |
|||
if not (1 <= nb_bits <= 8): |
|||
print(f"Le nombre de bits par couleur doit être entre 1 et 8. Nombre de bits entré :{nb_bits}") |
|||
return |
|||
# Ouvrir l'image et la convertir en RGB |
|||
image_ori = Image.open(img_name) |
|||
image_rgb = image_ori.convert("RGB") # Évite les problèmes liés à la transparence |
|||
largeur, hauteur = image_rgb.size |
|||
data_bytes = bytearray(image_rgb.tobytes()) |
|||
# De même pour le damier 8*8 |
|||
damier_ori = Image.open(damier_name) |
|||
damier_rgb = damier_ori.convert("RGB") |
|||
data_damier = bytearray(damier_rgb.tobytes()) |
|||
# Conversion du message à encoder en binaire |
|||
msg_bin = "".join(f"{ord(c):08b}" for c in msg) |
|||
msg_len_bin = f"{len(msg_bin):016b}" # On encode la taille sur 16 bits |
|||
message_complet = msg_len_bin + msg_bin # Str binaire |
|||
bit_index = 0 # Index dans le message binaire |
|||
blocs_modifies = [] # Permet de garder une trace des blocs qui ont été modifiés |
|||
for bloc_y in range(0, hauteur, 8): # On parcours tout les blocs de l'image |
|||
for bloc_x in range(0, largeur, 8): |
|||
bloc_pixels = [] |
|||
for y in range(8): |
|||
ligne_pixels = [] |
|||
for x in range(8): |
|||
pixel_x = bloc_x + x |
|||
pixel_y = bloc_y + y |
|||
if pixel_x >= largeur or pixel_y >= hauteur: |
|||
ligne_pixels.append(None) # Si le pixel est hors de l'image (pas multiple de 8), on ajoute None à la ligne puis on passe au suivant |
|||
continue |
|||
pixel = image_rgb.getpixel((pixel_x, pixel_y)) |
|||
ligne_pixels.append(pixel) |
|||
bloc_pixels.append(ligne_pixels) |
|||
comp = complexite(bloc_pixels) # On regarde la complexité du bloc |
|||
est_complexe = comp > seuil_complexite |
|||
#VERIF : print(f"Bloc ({bloc_x},{bloc_y}): Complexité = {comp}, {'Complexe' if est_complexe else 'Simple'}") |
|||
if not est_complexe or bit_index >= len(message_complet): # Si le bloc n'est pas complexe ou si le message est déjà entièrement encodé, on passe au bloc suivant |
|||
continue |
|||
blocs_modifies.append((bloc_x, bloc_y)) # Sinon on ajoute le bloc aux blocs modifiés |
|||
# Encodage dans le bloc complexe : |
|||
for y in range(8): |
|||
for x in range(8): |
|||
pixel_x = bloc_x + x |
|||
pixel_y = bloc_y + y |
|||
if pixel_x >= largeur or pixel_y >= hauteur: |
|||
continue # Évite de parcourir un pixel hors de l'image |
|||
pixel_index = (pixel_y * largeur + pixel_x) * 3 # Car 3 octets par pixel (R, G et B) |
|||
for couleur in range(3): # R, G et B |
|||
if bit_index >= len(message_complet): |
|||
break # On arrête si tout le message est encodé |
|||
byte = data_bytes[pixel_index + couleur] |
|||
byte_bin = list(f"{byte:08b}") # On vérifie que la chaîne fait bien 8 bits |
|||
# Modification des nb_bits les moins significatifs |
|||
for b in range(nb_bits): |
|||
if bit_index >= len(message_complet): |
|||
break |
|||
byte_bin[-(b + 1)] = message_complet[bit_index] |
|||
bit_index += 1 |
|||
data_bytes[pixel_index + couleur] = int("".join(byte_bin), 2) |
|||
if bit_index >= len(message_complet): |
|||
break # Sortir des boucles si message complet encodé |
|||
if bit_index >= len(message_complet): |
|||
break |
|||
if bit_index >= len(message_complet) or len(blocs_modifies) == 0: |
|||
continue |
|||
bloc_pixels_modifies = [] # Puisqu'on a modifier les octets du blocs, on doit vérifier s'il est encore complexe |
|||
for y in range(8): |
|||
ligne_pixels = [] |
|||
for x in range(8): |
|||
pixel_x = bloc_x + x |
|||
pixel_y = bloc_y + y |
|||
if pixel_x >= largeur or pixel_y >= hauteur: |
|||
ligne_pixels.append(None) |
|||
continue |
|||
# On reconstruit le pixel à partir de data_bytes modifié : |
|||
pixel_index = (pixel_y * largeur + pixel_x) * 3 |
|||
r = data_bytes[pixel_index] |
|||
g = data_bytes[pixel_index + 1] |
|||
b = data_bytes[pixel_index + 2] |
|||
pixel = (r, g, b) |
|||
ligne_pixels.append(pixel) |
|||
bloc_pixels_modifies.append(ligne_pixels) |
|||
nouvelle_complexite = complexite(bloc_pixels_modifies) |
|||
est_encore_complexe = nouvelle_complexite > seuil_complexite |
|||
#VERIF : print(f"Bloc ({bloc_x},{bloc_y}): Nouvelle complexité = {nouvelle_complexite}, {'Encore complexe' if est_encore_complexe else 'Devenu simple'}") |
|||
if not est_encore_complexe: # Si le bloc passe de complexe à simple, on applique un XOR avec le damier. |
|||
print(f"On applique le damier au bloc: ({bloc_x},{bloc_y})") |
|||
for y in range(8): |
|||
for x in range(8): |
|||
pixel_x = bloc_x + x |
|||
pixel_y = bloc_y + y |
|||
if pixel_x >= largeur or pixel_y >= hauteur: |
|||
continue |
|||
pixel_index = (pixel_y * largeur + pixel_x) * 3 |
|||
damier_index = (y * 8 + x) * 3 |
|||
for c in range(3): |
|||
data_bytes[pixel_index + c] ^= data_damier[damier_index + c] # XOR sur chaque octet d'un pixel |
|||
if bit_index < len(message_complet): # On vérifie si le message a été entièrement encodé |
|||
print(f"ATTENTION: Message incomplet! Seulement {bit_index}/{len(message_complet)} bits encodés.") |
|||
else: |
|||
print(f"Message entièrement encodé: {bit_index}/{len(message_complet)} bits.") |
|||
# Reconstruction de l'image |
|||
img_fin = Image.frombytes("RGB", image_rgb.size, bytes(data_bytes)) |
|||
img_fin.save(nom_img_fin) |
|||
print(f"Message encodé dans {nom_img_fin} avec {nb_bits} bit(s) par couleur.") |
|||
def bpc_discover(img_name: str, nb_bits: int = 1, seuil_complexite: int = 500): |
|||
""" |
|||
Une fonction qui permet de décoder un message précedment encoder à l'aide de la fonction bpc. |
|||
Entrées: |
|||
-img_name, str : nom de l'image contenant le message caché |
|||
-nb_bits, int : Nombre de bits de poids faible utilisés par couleur pour l'encodage |
|||
Sortie: Le message décodé, str |
|||
""" |
|||
if not (1 <= nb_bits <= 8): |
|||
print(f"Le nombre de bits par couleur doit être entre 1 et 8. Nombre de bits entré :{nb_bits}") |
|||
return |
|||
# On ouvre l'image |
|||
image = Image.open(img_name).convert("RGB") |
|||
largeur, hauteur = image.size |
|||
bits_lus = "" |
|||
taille_msg = None |
|||
total_bits = None |
|||
for bloc_y in range(0, hauteur, 8): # On lit les pixels bloc par bloc (8x8) |
|||
for bloc_x in range(0, largeur, 8): |
|||
bloc_pixels = [] |
|||
for y in range(8): |
|||
ligne_pixels = [] |
|||
for x in range(8): |
|||
pixel_x = bloc_x + x |
|||
pixel_y = bloc_y + y |
|||
if pixel_x >= largeur or pixel_y >= hauteur: |
|||
ligne_pixels.append(None) |
|||
continue |
|||
pixel = image.getpixel((pixel_x, pixel_y)) |
|||
ligne_pixels.append(pixel) |
|||
bloc_pixels.append(ligne_pixels) |
|||
comp = complexite(bloc_pixels) # On calcule la complexité |
|||
est_complexe = comp > seuil_complexite |
|||
if not est_complexe: |
|||
continue # Si le bloc n'est pas complexe, on passe au suivant |
|||
#VERIF : print(f"Lecture du bloc complexe ({bloc_x},{bloc_y}): Complexité = {comp}") |
|||
for y in range(8): # On lit les bits cachés dans le bloc complexe |
|||
for x in range(8): |
|||
pixel_x = bloc_x + x |
|||
pixel_y = bloc_y + y |
|||
if pixel_x >= largeur or pixel_y >= hauteur: |
|||
continue |
|||
r, g, b = image.getpixel((pixel_x, pixel_y)) |
|||
for couleur in (r, g, b): |
|||
for i in range(nb_bits): |
|||
bit = (couleur >> i) & 1 |
|||
bits_lus += str(bit) |
|||
if taille_msg is None and len(bits_lus) >= 16: |
|||
taille_msg = int(bits_lus[:16], 2) |
|||
total_bits = 16 + taille_msg |
|||
print(f"Taille du message : {taille_msg} bits") |
|||
if taille_msg is not None and len(bits_lus) >= total_bits: |
|||
break |
|||
if taille_msg is not None and len(bits_lus) >= total_bits: |
|||
break |
|||
if taille_msg is not None and len(bits_lus) >= total_bits: |
|||
break |
|||
if taille_msg is not None and len(bits_lus) >= total_bits: |
|||
break |
|||
if taille_msg is not None and len(bits_lus) >= total_bits: |
|||
break |
|||
if taille_msg is not None and len(bits_lus) >= total_bits: |
|||
break |
|||
if taille_msg is None: |
|||
print("Impossible de lire la taille du message.") |
|||
return "" |
|||
if len(bits_lus) < total_bits: |
|||
print(f"Message incomplet: seulement {len(bits_lus) - 16}/{taille_msg} bits lus") # On continue quand même avec les bits qu'on a |
|||
# Reconstruction du message |
|||
message_bits = bits_lus[16:16 + taille_msg] |
|||
if len(message_bits) % 8 != 0: |
|||
message_bits = message_bits + '0' * (8 - len(message_bits) % 8) |
|||
octets = [message_bits[i:i + 8] for i in range(0, len(message_bits), 8)] |
|||
message = "".join(chr(int(b, 2)) for b in octets) |
|||
print(f"MESSAGE DÉCODÉ ({len(bits_lus) - 16}/{taille_msg} bits): {message}") |
|||
return message |
|||
</code> |
|||
==Conclusion== |
|||
Nous pouvons conclure par une comparaison des deux méthodes.<br> |
|||
La stéganographie LSB permet de cacher une grande quantité d'informations. Cependant, elle est fortement visible à l'œil nu. Elle vaut le coup pour des messages courts mais devient moins utile dès lors que le message gagne en taille.<br> |
|||
La stéganographie BPC ne permet pas forcément de cacher autant d'informations, puisque cela dépend du nombre de blocs complexes. En contrepartie, elle est bien moins repérable et convient parfaitement à de longs messages.<br> |
|||
Dernière version du 18 mai 2025 à 23:54
Tuteur : Pierre Hyvernat
Elève : Hania Boudjaj
Introduction
Nous pouvons définir la stéganographie comme suit :
"Ensemble de techniques permettant de transmettre une information en la dissimulant au sein d'une autre information (photo, vidéo, texte, etc.) sans rapport avec la première et le plus souvent anodine, essentiellement à l'aide de logiciels spécialisés."
On attribue la première mention de la stéganographie telle que définie ci-dessus à l'historien grec Hérodote. Il décrit dans son ouvrage Historia, une tablette de bois gravée qu’on recouvre de cire de sorte à cacher un message.
Dans le cadre de ce projet, nous nous intéresserons à des algorithmes de stéganographie qui permettent de cacher du texte dans une image.
De plus, nous ne considérons pas les formats d'image avec compression.
La stéganographie LSB
Principe de base
Dans un premier temps, décomposons l'organisation d'une image :
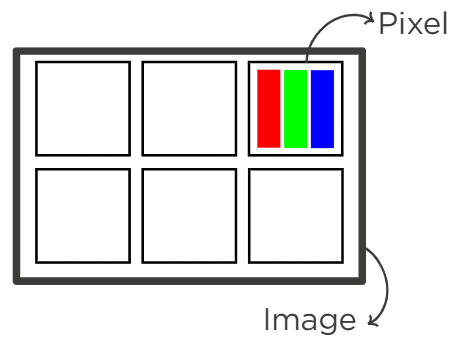
Une image est composée de pixels eux-mêmes composés de trois octets. Chacun de ces octets correspond à une composante couleur du pixel, Red, Green et Blue.
Chaque composante peut prendre une valeur allant de 0 à 255.
Ainsi, on peut modifier les n bits de poids faible d’un octet sans que cela soit visible à l'œil nu. Notons cependant que plus le poids du bit modifié augmente, plus la modification sera visible.
La stéganographie LSB permet donc de remplacer les n bits de poids faible des pixels d’une image par les bits d’une chaîne de caractère. On peut alors cacher un message dans une image.
Dans le cadre de ce projet, nous utiliserons la bibliothèque Pillow qui permet de manipuler facilement des images.
Exemples
| Image originale. | Image modifiée sur 1 bit de poids faible. |
Code
from PIL import Image
def cache(img_name: str, msg: str, nom_img_fin: str, nb_bits: int = 1, ):
if not (1 <= nb_bits <= 8):
print("Le nombre de bits par couleur doit être entre 1 et 8.")
return
# Ouvrir et convertir l'image en mode RGB :
image_ori = Image.open(img_name)
image_rgb = image_ori.convert("RGB") # Evite les problèmes liés à la transparence.
data_bytes = bytearray(image_rgb.tobytes())
# Encodage du message en binaire.
msg_bin = "".join((f"{ord(c):08b}") for c in msg )
msg_len = len(msg_bin)
msg_len_bin = f"{msg_len:016b}" # 16 bits pour représenter la taille du message
message_complet = msg_len_bin + msg_bin
# Vérification de la capacité
capacite = len(data_bytes) * nb_bits
if len(message_complet) > capacite:
print(f"Le message est trop long pour être encodé dans cette image avec {str(nb_bits)} bit(s) par couleur.")
return
# Encodage dans le bytearray.
bit_index = 0
for i in range(len(data_bytes)):
byte = data_bytes[i]
for b in range(nb_bits):
if bit_index >= len(message_complet):
break
# Remplacer les bits les moins significatifs
message_bit = int(message_complet[bit_index])
bit_index += 1
byte &= ~(1 << b)
byte |= (message_bit << b)
data_bytes[i] = byte
if bit_index >= len(message_complet):
break
# Reconstruction de l'image.
img_fin = Image.frombytes("RGB", image_rgb.size, bytes(data_bytes))
img_fin.save(nom_img_fin)
print(f"Message encodé avec succès dans {nom_img_fin}avec {str(nb_bits)} bit(s) par couleur.")
def discover(img_name: str, nb_bits: int = 1):
if not (1 <= nb_bits <= 8):
print("Le nombre de bits par couleur doit être entre 1 et 8.")
return
# Ouvrir l'image.
image_ori = Image.open(img_name)
image_rgb = image_ori.convert("RGB")
data_bytes = bytearray(image_rgb.tobytes())
bits_lus = ""
taille_msg = None
valeur = 0
for byte in data_bytes:
for b in range(nb_bits):
bit = (byte >> b) & 1
bits_lus += str(bit)
# Lecture des 16 premiers bits, qui contiennent la taille.
if len(bits_lus) == 16 and taille_msg is None:
for i in range(16):
valeur = (valeur << 1) | (1 if bits_lus[i] == '1' else 0)
taille_msg = valeur
total_bits = 16 + taille_msg
if taille_msg is not None and len(bits_lus) >= total_bits:
break
if taille_msg is not None and len(bits_lus) >= total_bits:
break
# Reconstruction du message.
message_bits = bits_lus[16:16 + taille_msg]
octets = [message_bits[i:i+8] for i in range(0, len(message_bits), 8)]
message = "".join(chr(int(o, 2)) for o in octets)
print(f"MESSAGE DÉCODÉ : {message}")
return message
Problème
Plus la taille du message à cacher est importante, plus le nombre de bits nécessaires à l’encodage augmente.
| Image modifiée sur 4 bits de poids faible. |
Or, comme mentionné plus tôt, plus le poids du bit modifié augmente, plus l'altération sera visible.
Pour remédier à ce problème, nous pouvons nous tourner vers la Stéganographie BPC.
La stéganographie BPC
Principe de base
Contrairement à la stéganographie LSB, nous allons maintenant choisir dans quelles parties de l’image cacher notre message. Pour cela, nous allons nous intéresser à la complexité d’une image :
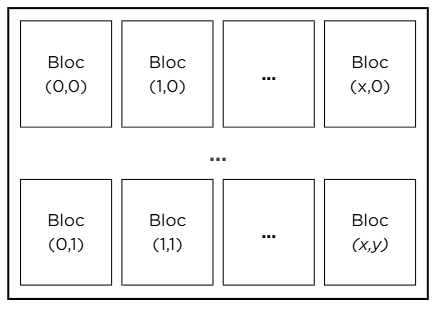
Soit une image composée de pixels RGB. Nous allons diviser cette image en blocs de 8*8 pixels.
Pour décider si oui ou non nous cachons une partie du message dans le bloc actuel, nous allons calculer sa complexité.
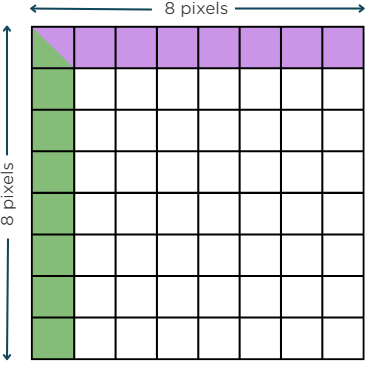
Pour cela, il suffit de compter le nombre de changements entre deux bits consécutifs pour chaque ligne et chaque colonne du bloc.
Plus le nombre de changements est élevé dans un bloc, plus il est complexe. Nous fixerons un seuil de complexité arbitraire. Si le nombre de changements est supérieur à ce seuil, le bloc est complexe. Sinon, il est simple.
Intervient alors un nouveau problème : lorsqu’on encode une partie du message, il y est possible que le bloc change soudainement de complexité (si, dû aux changements effectués sur les bits, le nombre de changement diminue), ce qui pose problème pour le décodage.
Pour y remédier, nous effectuons l’opération arithmétique XOR entre le bloc et un damier :
Un damier de 8*8 pixels correspond simplement à une suite de pixels noirs et pixels blancs. On peut ainsi le représenter par une succession de 3 canaux RGB fixés à 0 suivis de 3 canaux RGB fixés à F (en base 16).
On obtient alors deux suites d'octets de même longueur qu'on peut "XOR" l'une avec l'autre.
Cette méthode permet de faire passer la complexité d’un bloc de simple à complexe. Elle est donc appliquée sur tous les blocs qui étaient classés comme "complexe", et dans lesquels on à caché une partie du message, qui sont ensuite passés à "simple".
Exemples
| Image originale. | Image modifiée sur 1 bit de poids faible. |
Image modifiée sur 4 bits de poids faible. |
Image modifiée sur 8 bits. |
Code
from PIL import Image
def complexite(bloc_pixels):
"""
Une fonction qui permet de calculer la complexité d'un bloc de 8*8 pixels.
Entrée : Un tableau qui contient les pixels du bloc actuel.
Sortie : int, un compteur qui indique le nombre de changements de bits consécutifs.
"""
changement = 0
# On regarde la complexité des colonnes (pixels de même x) :
for x in range(len(bloc_pixels[0])):
for couleur in range(3): # Pour chaque composante RGB
for bit_pos in range(8): # Pour chaque position de bit (de 0 à 7)
prev_bit = None # Parce qu'au début il n'y a pas de bit précédent
for y in range(len(bloc_pixels)):
if bloc_pixels[y][x] is None:
continue
bit = (bloc_pixels[y][x][couleur] >> bit_pos) & 1 # On extrait le bit spécifique de la composante couleur RGB
if prev_bit is not None and bit != prev_bit: # On regarde s'il y a un chagement entre deux bits consécutifs
changement += 1
prev_bit = bit
# On regarde la complexité des lignes (pixels de même y) :
for y in range(len(bloc_pixels)):
for couleur in range(3):
for bit_pos in range(8):
prev_bit = None
for x in range(len(bloc_pixels[0])):
if bloc_pixels[y][x] is None:
continue
bit = (bloc_pixels[y][x][couleur] >> bit_pos) & 1
if prev_bit is not None and bit != prev_bit:
changement += 1
prev_bit = bit
return changement
def bpc(img_name: str, msg: str, nom_img_fin: str = "BPC8bis2.png", damier_name: str = "damier.png", nb_bits: int = 1, seuil_complexite: int = 500):
"""
Une fonction qui permet de caché un message dans une image en fonction de la complexité de blocs 8*8 pixels.
Entrées :
-img_name : Nom de l'image d'origine
-msg : message à caché
-nom_img_fin : nom de l'image qui contient le message caché
-damier_name : nom de l'image qui contient le damier
-nb_bits : nombre de bits sur lesquels on encode le message
Sortie : img_fin, une image qui contient un message.
"""
if not (1 <= nb_bits <= 8):
print(f"Le nombre de bits par couleur doit être entre 1 et 8. Nombre de bits entré :{nb_bits}")
return
# Ouvrir l'image et la convertir en RGB
image_ori = Image.open(img_name)
image_rgb = image_ori.convert("RGB") # Évite les problèmes liés à la transparence
largeur, hauteur = image_rgb.size
data_bytes = bytearray(image_rgb.tobytes())
# De même pour le damier 8*8
damier_ori = Image.open(damier_name)
damier_rgb = damier_ori.convert("RGB")
data_damier = bytearray(damier_rgb.tobytes())
# Conversion du message à encoder en binaire
msg_bin = "".join(f"{ord(c):08b}" for c in msg)
msg_len_bin = f"{len(msg_bin):016b}" # On encode la taille sur 16 bits
message_complet = msg_len_bin + msg_bin # Str binaire
bit_index = 0 # Index dans le message binaire
blocs_modifies = [] # Permet de garder une trace des blocs qui ont été modifiés
for bloc_y in range(0, hauteur, 8): # On parcours tout les blocs de l'image
for bloc_x in range(0, largeur, 8):
bloc_pixels = []
for y in range(8):
ligne_pixels = []
for x in range(8):
pixel_x = bloc_x + x
pixel_y = bloc_y + y
if pixel_x >= largeur or pixel_y >= hauteur:
ligne_pixels.append(None) # Si le pixel est hors de l'image (pas multiple de 8), on ajoute None à la ligne puis on passe au suivant
continue
pixel = image_rgb.getpixel((pixel_x, pixel_y))
ligne_pixels.append(pixel)
bloc_pixels.append(ligne_pixels)
comp = complexite(bloc_pixels) # On regarde la complexité du bloc
est_complexe = comp > seuil_complexite
#VERIF : print(f"Bloc ({bloc_x},{bloc_y}): Complexité = {comp}, {'Complexe' if est_complexe else 'Simple'}")
if not est_complexe or bit_index >= len(message_complet): # Si le bloc n'est pas complexe ou si le message est déjà entièrement encodé, on passe au bloc suivant
continue
blocs_modifies.append((bloc_x, bloc_y)) # Sinon on ajoute le bloc aux blocs modifiés
# Encodage dans le bloc complexe :
for y in range(8):
for x in range(8):
pixel_x = bloc_x + x
pixel_y = bloc_y + y
if pixel_x >= largeur or pixel_y >= hauteur:
continue # Évite de parcourir un pixel hors de l'image
pixel_index = (pixel_y * largeur + pixel_x) * 3 # Car 3 octets par pixel (R, G et B)
for couleur in range(3): # R, G et B
if bit_index >= len(message_complet):
break # On arrête si tout le message est encodé
byte = data_bytes[pixel_index + couleur]
byte_bin = list(f"{byte:08b}") # On vérifie que la chaîne fait bien 8 bits
# Modification des nb_bits les moins significatifs
for b in range(nb_bits):
if bit_index >= len(message_complet):
break
byte_bin[-(b + 1)] = message_complet[bit_index]
bit_index += 1
data_bytes[pixel_index + couleur] = int("".join(byte_bin), 2)
if bit_index >= len(message_complet):
break # Sortir des boucles si message complet encodé
if bit_index >= len(message_complet):
break
if bit_index >= len(message_complet) or len(blocs_modifies) == 0:
continue
bloc_pixels_modifies = [] # Puisqu'on a modifier les octets du blocs, on doit vérifier s'il est encore complexe
for y in range(8):
ligne_pixels = []
for x in range(8):
pixel_x = bloc_x + x
pixel_y = bloc_y + y
if pixel_x >= largeur or pixel_y >= hauteur:
ligne_pixels.append(None)
continue
# On reconstruit le pixel à partir de data_bytes modifié :
pixel_index = (pixel_y * largeur + pixel_x) * 3
r = data_bytes[pixel_index]
g = data_bytes[pixel_index + 1]
b = data_bytes[pixel_index + 2]
pixel = (r, g, b)
ligne_pixels.append(pixel)
bloc_pixels_modifies.append(ligne_pixels)
nouvelle_complexite = complexite(bloc_pixels_modifies)
est_encore_complexe = nouvelle_complexite > seuil_complexite
#VERIF : print(f"Bloc ({bloc_x},{bloc_y}): Nouvelle complexité = {nouvelle_complexite}, {'Encore complexe' if est_encore_complexe else 'Devenu simple'}")
if not est_encore_complexe: # Si le bloc passe de complexe à simple, on applique un XOR avec le damier.
print(f"On applique le damier au bloc: ({bloc_x},{bloc_y})")
for y in range(8):
for x in range(8):
pixel_x = bloc_x + x
pixel_y = bloc_y + y
if pixel_x >= largeur or pixel_y >= hauteur:
continue
pixel_index = (pixel_y * largeur + pixel_x) * 3
damier_index = (y * 8 + x) * 3
for c in range(3):
data_bytes[pixel_index + c] ^= data_damier[damier_index + c] # XOR sur chaque octet d'un pixel
if bit_index < len(message_complet): # On vérifie si le message a été entièrement encodé
print(f"ATTENTION: Message incomplet! Seulement {bit_index}/{len(message_complet)} bits encodés.")
else:
print(f"Message entièrement encodé: {bit_index}/{len(message_complet)} bits.")
# Reconstruction de l'image
img_fin = Image.frombytes("RGB", image_rgb.size, bytes(data_bytes))
img_fin.save(nom_img_fin)
print(f"Message encodé dans {nom_img_fin} avec {nb_bits} bit(s) par couleur.")
def bpc_discover(img_name: str, nb_bits: int = 1, seuil_complexite: int = 500):
"""
Une fonction qui permet de décoder un message précedment encoder à l'aide de la fonction bpc.
Entrées:
-img_name, str : nom de l'image contenant le message caché
-nb_bits, int : Nombre de bits de poids faible utilisés par couleur pour l'encodage
Sortie: Le message décodé, str
"""
if not (1 <= nb_bits <= 8):
print(f"Le nombre de bits par couleur doit être entre 1 et 8. Nombre de bits entré :{nb_bits}")
return
# On ouvre l'image
image = Image.open(img_name).convert("RGB")
largeur, hauteur = image.size
bits_lus = ""
taille_msg = None
total_bits = None
for bloc_y in range(0, hauteur, 8): # On lit les pixels bloc par bloc (8x8)
for bloc_x in range(0, largeur, 8):
bloc_pixels = []
for y in range(8):
ligne_pixels = []
for x in range(8):
pixel_x = bloc_x + x
pixel_y = bloc_y + y
if pixel_x >= largeur or pixel_y >= hauteur:
ligne_pixels.append(None)
continue
pixel = image.getpixel((pixel_x, pixel_y))
ligne_pixels.append(pixel)
bloc_pixels.append(ligne_pixels)
comp = complexite(bloc_pixels) # On calcule la complexité
est_complexe = comp > seuil_complexite
if not est_complexe:
continue # Si le bloc n'est pas complexe, on passe au suivant
#VERIF : print(f"Lecture du bloc complexe ({bloc_x},{bloc_y}): Complexité = {comp}")
for y in range(8): # On lit les bits cachés dans le bloc complexe
for x in range(8):
pixel_x = bloc_x + x
pixel_y = bloc_y + y
if pixel_x >= largeur or pixel_y >= hauteur:
continue
r, g, b = image.getpixel((pixel_x, pixel_y))
for couleur in (r, g, b):
for i in range(nb_bits):
bit = (couleur >> i) & 1
bits_lus += str(bit)
if taille_msg is None and len(bits_lus) >= 16:
taille_msg = int(bits_lus[:16], 2)
total_bits = 16 + taille_msg
print(f"Taille du message : {taille_msg} bits")
if taille_msg is not None and len(bits_lus) >= total_bits:
break
if taille_msg is not None and len(bits_lus) >= total_bits:
break
if taille_msg is not None and len(bits_lus) >= total_bits:
break
if taille_msg is not None and len(bits_lus) >= total_bits:
break
if taille_msg is not None and len(bits_lus) >= total_bits:
break
if taille_msg is not None and len(bits_lus) >= total_bits:
break
if taille_msg is None:
print("Impossible de lire la taille du message.")
return ""
if len(bits_lus) < total_bits:
print(f"Message incomplet: seulement {len(bits_lus) - 16}/{taille_msg} bits lus") # On continue quand même avec les bits qu'on a
# Reconstruction du message
message_bits = bits_lus[16:16 + taille_msg]
if len(message_bits) % 8 != 0:
message_bits = message_bits + '0' * (8 - len(message_bits) % 8)
octets = [message_bits[i:i + 8] for i in range(0, len(message_bits), 8)]
message = "".join(chr(int(b, 2)) for b in octets)
print(f"MESSAGE DÉCODÉ ({len(bits_lus) - 16}/{taille_msg} bits): {message}")
return message
Conclusion
Nous pouvons conclure par une comparaison des deux méthodes.
La stéganographie LSB permet de cacher une grande quantité d'informations. Cependant, elle est fortement visible à l'œil nu. Elle vaut le coup pour des messages courts mais devient moins utile dès lors que le message gagne en taille.
La stéganographie BPC ne permet pas forcément de cacher autant d'informations, puisque cela dépend du nombre de blocs complexes. En contrepartie, elle est bien moins repérable et convient parfaitement à de longs messages.