« Projets étudiants cryptographie et sécurité/Choulet Ravry Enigma » : différence entre les versions
(Ajout image intro) |
|||
| (69 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
[[Fichier:Enigma_1940.jpeg|thumb|La machine enigma (modèle de 1940)]] |
[[Fichier:Enigma_1940.jpeg|thumb|La machine enigma (modèle de 1940)]] |
||
La machine Enigma est une machine de chiffrement et de déchiffrement de messages. Elle a été inventée |
La machine Enigma est une machine de chiffrement et de déchiffrement de messages. Elle a été inventée au début du XXème siècle par Arthur Scherbius, un ingénieur en électricité allemand. Alors réputée inviolable, elle sera utilisée par les forces armées allemandes pour chiffrer l'ensemble des communications militaires durant la seconde guerre mondiale. |
||
Le chiffrement sera craqué durant la guerre par les britanniques, grâce aux efforts d'avant guerre des services de renseignement Français et Polonais. Le déchiffrement des messages allemands a contribué à la victoire des alliés |
Le chiffrement sera craqué durant la guerre par les britanniques, grâce aux efforts d'avant guerre des services de renseignement Français et Polonais. Le déchiffrement des messages allemands a contribué à la victoire des alliés et aurait, selon certaines estimations, écourtée la guerre en Europe d'environ deux ans. |
||
== Histoire de la machine Enigma == |
== Histoire de la machine Enigma == |
||
Arthur Sherbius est né en 1878. Il étudie l'ingénierie électrique à Munich puis à Hanovre. Il commencera par s'intéresser aux systèmes de turbines à eau dans sa thèse en 1903. En 1918, il crée son entreprise « Scherbius & Ritter » et dépose le brevet d'une machine électromécanique de chiffrement novatrice. Basée sur un système de rotors, la machine permet un très grand nombre de permutations et offre donc une très grande sécurité. L'idée est donne mais Shrebius ne sera pas le seul à l'avoir. En l'espace de quatre ans, trois autres brevets seront déposés pour des machines similaires aux Etats-Unis, en Suède et aux Pays-Bas. |
|||
Sherbius tente alors de commercialiser sa machine mais c'est un échec. La machine est trop chère (environ 30 000€) et n'intéresse presque personne. Après le refus de la marine allemande et du ministère des chiffres allemand à la fin des années 1910, il se tourne alors vers le secteur privé, sans grand succès. Ce n'est qu'en 1926 que la marine allemande (la Kriegsmarine) se ré-intéressera à un modèle amélioré de la machine Enigma : le modèle Enigma-D. Le même modèle sera adopté en 1929 par l'armée de terre, suivie par l'ensemble de l'organisation militaire allemande. Surnommée "la machine M", le modèle initial subira de nombreuses modifications au cours de la guerre, pour tenter d'en renforcer la sécurité. |
|||
Malheureusement pour lui, Sherbius ne verra pas le succès de sa machine, il meurt en 1929, à l'âge de 41 ans, sous les ruades d'un cheval attelé à une carriole. |
|||
== Description physique de la machine == |
|||
[[Fichier:Enigma_face.jpg|300px|thumb|Vue de dessus de la machine Enigma. A gauche, capot fermé, à droite, capot ouvert avec les rotors visibles]] |
|||
La machine Enigma est une machine dite électromécanique. Elle est donc constituée d'une partie mécanique et d'une partie électrique. La partie mécanique est essentiellement composé d'un clavier, de multiples rotors, d'un réflecteur et d'un système de rotation des rotors. La partie électrique est composé d'un système d'interrupteurs, de multiples lampes (autant que de touches) et d'un tableau de connexion. |
|||
=== Les rotors === |
|||
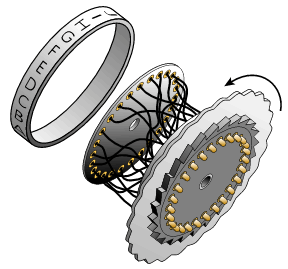
Les rotors sont la base de la machine Enigma. D'un diamètre d'environ 10cm, le rotor est un disque de caoutchouc dur ou de bakélite et comporte 2 faces bien distinctes. |
|||
Sur l'une des faces sont disposé des contacts à aiguilles, équipés de ressorts (ce sont des contacts actifs). Sur l'autre face sont disposés le même nombre de contacts mais quant à eux, de type plats (contacts passifs). |
|||
Ces contacts sont aux nombres de 26 par faces (pour représenter l'alphabet). |
|||
<gallery perrow="3" mode=packed align="center"> |
|||
Fichier:Enigma-rotors.jpg |
|||
Fichier:Rotor-pin-contacts.jpg|Face montrant les contacts à aiguilles du rotor |
|||
Fichier:Rotor-flat-contacts.jpg|Face montrant les contacts plats du rotor |
|||
</gallery> |
|||
Vous l'avez compris, lorsque l'on place les rotors les uns en face des autres, les contacts à aiguilles d'un rotor se positionnent en face des contacts plats du rotor voisin. Le contact entre les 2 rotors va ainsi former la connexion électrique. |
|||
Pour complexifier le tout, les connexions entre les contacts plats et à aiguilles d'un même rotor sont assurées par un ensemble de 26 câbles électriques, et ce, selon un schéma compliqué. Par exemple, sur un rotor en particulier, le contacteur n°1 d'une face va peut-être être connecté au contacteur n°13 de la face opposée. Les machines Enigma possède un jeu de plusieurs rotors, tous possédant des connexions internes différentes. En réalité un rotor seul effectue une opération très simple - un [https://fr.wikipedia.org/wiki/Histoire_de_la_cryptologie#Les_premiers_.C2.AB_vrais_.C2.BB_syst.C3.A8mes_de_cryptographie chiffrage par substitution]. La complexité de cette machine, provient de l'utilisation de trois ou quatre rotors couplé à un réflecteur (dont nous parlerons après) et du mécanisme d'entraînement des rotors. |
|||
[[Fichier:rotor-exploded.gif|250px|thumb|centré|Vue explosée d'un rotor et de la connexion entre les 2 faces de celui-ci]] |
|||
=== Mécanisme de rotation des rotors === |
|||
Le mécanisme d'entraînement des rotor à pour but de complexifier le chiffrement par substitution des rotors en permettant la rotation des rotors. Les rotors, composés d'une roue de 26 dents et d'un anneau métallique à encoches, solidaire du rotor. A chaque frappe de clavier, le mécanisme appuie sur la roue de chaque rotor pour la faire avancer d'un cran. Les anneaux métalliques, quand à eux, contrôlent la rotation ou non des rotors. Pour qu'un rotor puisse tournée, il fallait que l'anneau du rotor de gauche, présente une encoche alignée avec son cliquet. Le premier rotor n'étant pas bloqué par un anneau, avance d'un cran à chaque touche pressée. Ainsi l'on dispose d'un système quelque peu similaire à un odomètre. |
|||
Le mécanisme pourrait s'arrêter la. La première roue avance d'un cran à chaque frappe, la seconde avance d'un cran à chaque tour de la première roue, etc. Toutefois, le mécanisme pouvait inclure une "double avancée". Au moment d'effectuer la rotation du troisième rotor, le système pouvait pousser sur l'encoche du précédent rotor. Ainsi, à la fois le dernier rotor et le second rotor avançaient d'un cran. C'est ce fonctionnement qui fait varier ce mécanisme de celui d'un odomètre. |
|||
=== Le Réflecteur === |
|||
[[Fichier:reflector.png|thumb|centré|264px]] |
|||
Excepté les premiers modèles des machines Enigma, le dernier rotor était suivi d'un réflecteur. Le réflecteur connecte les sorties du dernier rotor (contacts plats) par pair. Ainsi, le courant arrivant dans le réflecteur va repartir dans le dernier rotor et reparcourir les rotors dans le sens inverse mais en empruntant un chemin différent. |
|||
Suivant les versions des machines, le réflecteur pouvait être inséré dans plusieurs positions ou pouvait encore subir le même mécanisme de rotation que les rotors. |
|||
=== La table de permutations === |
|||
La table (ou tableau) de permutations ( ou connexion) avait pour objectif d'ajouter encore plus de complexité en passant par une dernière étape de substitution. La table, composé de 26 lettres, permet d'encoder les lettres deux à deux. Ainsi, si après l'étape des rotors, le courant se dirigeait vers A et que A était permuté à X, X s'allumerait. Cette étape, peu importante soit-elle, permettait d'ajouter de la complexité simplement. |
|||
Le nombre de permutations à établir était de 20 sur 26. |
|||
=== Fonctionnement en détails === |
|||
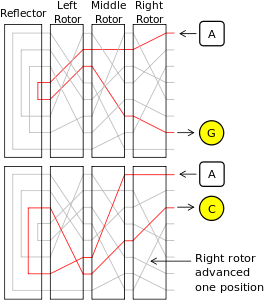
[[Fichier:schemaEnigma.png|300px|thumb|centré|Le fonctionnement en diverses étapes du chiffrement]] |
|||
Dans le détail : |
|||
1- La première étape correspond à la mise sous tension de la machine à l'aide de la batterie. Sans cela, impossible d'envoyer un signal via les interrupteurs. |
|||
2- Ensuite on presse une touche du clavier (dans notre exemple, c'est la touche A) pour envoyer le courant à la table de permutation. |
|||
3- Le courant est envoyé à la case A de la table de permutations. Il se trouve que A n'est permuté avec aucune lettre donc rien ne se produit. |
|||
4- Le courant se dirige ensuite vers le premier rotor. |
|||
5- Il continue son chemin dans les rotors suivants. |
|||
6- Il passe dans le réflecteur puis effectue un second passage dans les rotors (différent du premier passage). |
|||
7- La lettre chiffré est S. Le courant se dirige donc à nouveau vers la table des permutations, à la case S. |
|||
8- Celle-ci est permutée avec D, le signal passe donc dans la case D. |
|||
9- La lampe correspondante s'allume. Ici, la lampe D s'éclaire. |
|||
Notre lettre A chiffrée devient donc D. Une fois le signal passé dans le circuit, le rotor effectue sa rotation. |
|||
== Principe de chiffrement == |
|||
Le chiffrement de la machine Enigma est un chiffrement polyalphabétique. Contrairement à des chiffrements similaires comme Vigenère, il n'y a pas de clé. Chaque fois que l'on appuie sur une touche et que les rotors tournent, un nouvel alphabet de substitution est utilisé. Il y a 26 permutations possibles par rotor soit 26*26*26 = 17576 alphabets de substitution. De plus, l'ordre dans lequel ces alphabets sont utilisés dépend de la position de départ de chaque rotor, des rotors utilisés, et de l'ordre dans lequel ils sont installés dans la machine. |
|||
Le nombre de combinaisons possibles peut être calculé en tenant compte de la position des rotors, du nombre possible d'alphabets de substitution et des branchements du tableau de connexion. Sur les machines standards, on choisit 3 rotors parmi 5 soit <math>A^3_5 = \dfrac{5!}{2!}\ = 5 \times 4 \times3 = 60</math> possibilités. Le nombre d'alphabets de substitution, calculé précédemment, est de 17576. Enfin, on permute 20 lettres parmis 26 sur le tableau de connexion ce qui nous donne <math>\dfrac{26!}{6! \times 10! \times 2^{10}} = 150\,738\,274\,937\,250</math> permutations possibles. Si l'on multiplie ces trois chiffres, on obtient <math>1,59 \times 10^{20}</math> combinaisons possibles au total. Ce qui est énorme pour l'époque, étant donné qu'il faudrait tester toutes les possibilités à la main, une par une, pour craquer un message en utilisant une attaque par brute force. |
|||
== Mise en oeuvre == |
|||
[[Fichier:Enigma_code_book.jpeg|thumb|Livre contenant les codes pour chaque jour (fermé)]] |
|||
[[Fichier:Enigma_livre_instructions.jpeg|thumb|Livre contenant les codes pour chaque jour (ouvert)]] |
|||
Le chiffrement et le déchiffrement d'un message sont effectués manuellement par une équipe de deux chiffreurs selon une procédure très précise. |
|||
=== Préparation de la machine === |
|||
Avant de commencer le chiffrement à proprement dit du message, plusieurs réglages de la machine sont nécessaires. Ces réglages changent régulièrement de manière mensuelle, hebdomadaire ou quotidienne selon les réglages et les corps d'armées. Les instructions de réglages sont contenues dans des livres détenus par les chiffreurs. Les étapes à suivre sont les suivantes : |
|||
# Choix et positionnement des rotors dans le bon ordre, selon les instructions du jour. Par exemple le rotor I, puis le rotor IV puis le rotor II, notée I-IV-II dans le livre d'instructions. |
|||
# Positionnement de la bague des trois rotors, selon les instructions du jour. Par exemple la bague du premier rotor sur la position 06, celle du deuxième sur 20 et la dernière sur 24, notée FTX dans le livre d'instructions. |
|||
# Branchements sur le tableau de connexions, selon les instructions du jour. Par exemple, U avec A, P avec C, etc ..., notée UA-PC-... dans le livre d'instructions. |
|||
# Un des chiffreurs (appelons le Chiffreur 1) positionne alors les rotors sur les positions indiquées dans le livre d'instructions. Par exemple JCM. |
|||
# Chiffreur1 choisit alors une position aléatoire des rotors, mais ne modifie pas encore leur position pour l'instant. C'est la '''clé brute du message'''. Prenons BGZ pour l'exemple. Il tape alors deux fois la clé sur la machine (BGZBGZ). |
|||
# Le deuxième chiffreur note le résultat affiché par les voyant : c'est le clé chiffrée. |
|||
# Le premier chiffreur dispose alors les rotors selon la position qu'il a choisit au préalable. Le chiffrement du message peut commencer. |
|||
=== Envoi d'un message chiffré === |
|||
Afin de chiffrer le message, le premier chiffreur tape les lettres du message une par une, et le deuxième chiffreur note le chiffré de chaque lettre (donné par la LED allumée). |
|||
Un message commence toujours par des indicateurs permettant d'identifier l’émetteur ainsi que la date et l'heure d'émission ainsi que le nombre de lettre du message. On trouve ensuite un indicateur de 5 lettres qui identifient le réseau Enigma et permet d'identifier le livre d'instructions utilisé pour le chiffrement (donc celui à utiliser pour le déchiffrement). Vient ensuite la clé chiffrée puis le corps du message. |
|||
Afin de renforcer la sécurité, les allemands codaient certains mots ou expressions et transposaient les coordonnées géographiques. Ainsi, même déchiffrés, certains messages n'avaient toujours aucun sens pour un non initié. |
|||
Les opérateurs envoient ensuite la message en morse au moyen d'un poste radio. |
|||
=== Réception et déchiffrement du message === |
|||
Lorsque le destinataire reçoit le message depuis un poste radio il le note sur un bout de papier et le confie à un chiffreur. Pour déchiffrer, le chiffreur suit les mêmes étapes de préparations (1 à 4), selon les instructions du registre utilisé par l'émetteur. Il obtient alors la clé brute en tapant la clé chiffrée sur la machine. Il positionne alors les rotors selon les positions indiquées par la clé et déchiffre le message en tapant chaque lettre une à une et en notant le résultat. |
|||
Dernière version du 20 mars 2016 à 18:36
La machine Enigma est une machine de chiffrement et de déchiffrement de messages. Elle a été inventée au début du XXème siècle par Arthur Scherbius, un ingénieur en électricité allemand. Alors réputée inviolable, elle sera utilisée par les forces armées allemandes pour chiffrer l'ensemble des communications militaires durant la seconde guerre mondiale.
Le chiffrement sera craqué durant la guerre par les britanniques, grâce aux efforts d'avant guerre des services de renseignement Français et Polonais. Le déchiffrement des messages allemands a contribué à la victoire des alliés et aurait, selon certaines estimations, écourtée la guerre en Europe d'environ deux ans.
Histoire de la machine Enigma
Arthur Sherbius est né en 1878. Il étudie l'ingénierie électrique à Munich puis à Hanovre. Il commencera par s'intéresser aux systèmes de turbines à eau dans sa thèse en 1903. En 1918, il crée son entreprise « Scherbius & Ritter » et dépose le brevet d'une machine électromécanique de chiffrement novatrice. Basée sur un système de rotors, la machine permet un très grand nombre de permutations et offre donc une très grande sécurité. L'idée est donne mais Shrebius ne sera pas le seul à l'avoir. En l'espace de quatre ans, trois autres brevets seront déposés pour des machines similaires aux Etats-Unis, en Suède et aux Pays-Bas.
Sherbius tente alors de commercialiser sa machine mais c'est un échec. La machine est trop chère (environ 30 000€) et n'intéresse presque personne. Après le refus de la marine allemande et du ministère des chiffres allemand à la fin des années 1910, il se tourne alors vers le secteur privé, sans grand succès. Ce n'est qu'en 1926 que la marine allemande (la Kriegsmarine) se ré-intéressera à un modèle amélioré de la machine Enigma : le modèle Enigma-D. Le même modèle sera adopté en 1929 par l'armée de terre, suivie par l'ensemble de l'organisation militaire allemande. Surnommée "la machine M", le modèle initial subira de nombreuses modifications au cours de la guerre, pour tenter d'en renforcer la sécurité.
Malheureusement pour lui, Sherbius ne verra pas le succès de sa machine, il meurt en 1929, à l'âge de 41 ans, sous les ruades d'un cheval attelé à une carriole.
Description physique de la machine
La machine Enigma est une machine dite électromécanique. Elle est donc constituée d'une partie mécanique et d'une partie électrique. La partie mécanique est essentiellement composé d'un clavier, de multiples rotors, d'un réflecteur et d'un système de rotation des rotors. La partie électrique est composé d'un système d'interrupteurs, de multiples lampes (autant que de touches) et d'un tableau de connexion.
Les rotors
Les rotors sont la base de la machine Enigma. D'un diamètre d'environ 10cm, le rotor est un disque de caoutchouc dur ou de bakélite et comporte 2 faces bien distinctes. Sur l'une des faces sont disposé des contacts à aiguilles, équipés de ressorts (ce sont des contacts actifs). Sur l'autre face sont disposés le même nombre de contacts mais quant à eux, de type plats (contacts passifs). Ces contacts sont aux nombres de 26 par faces (pour représenter l'alphabet).
Vous l'avez compris, lorsque l'on place les rotors les uns en face des autres, les contacts à aiguilles d'un rotor se positionnent en face des contacts plats du rotor voisin. Le contact entre les 2 rotors va ainsi former la connexion électrique. Pour complexifier le tout, les connexions entre les contacts plats et à aiguilles d'un même rotor sont assurées par un ensemble de 26 câbles électriques, et ce, selon un schéma compliqué. Par exemple, sur un rotor en particulier, le contacteur n°1 d'une face va peut-être être connecté au contacteur n°13 de la face opposée. Les machines Enigma possède un jeu de plusieurs rotors, tous possédant des connexions internes différentes. En réalité un rotor seul effectue une opération très simple - un chiffrage par substitution. La complexité de cette machine, provient de l'utilisation de trois ou quatre rotors couplé à un réflecteur (dont nous parlerons après) et du mécanisme d'entraînement des rotors.
Mécanisme de rotation des rotors
Le mécanisme d'entraînement des rotor à pour but de complexifier le chiffrement par substitution des rotors en permettant la rotation des rotors. Les rotors, composés d'une roue de 26 dents et d'un anneau métallique à encoches, solidaire du rotor. A chaque frappe de clavier, le mécanisme appuie sur la roue de chaque rotor pour la faire avancer d'un cran. Les anneaux métalliques, quand à eux, contrôlent la rotation ou non des rotors. Pour qu'un rotor puisse tournée, il fallait que l'anneau du rotor de gauche, présente une encoche alignée avec son cliquet. Le premier rotor n'étant pas bloqué par un anneau, avance d'un cran à chaque touche pressée. Ainsi l'on dispose d'un système quelque peu similaire à un odomètre.
Le mécanisme pourrait s'arrêter la. La première roue avance d'un cran à chaque frappe, la seconde avance d'un cran à chaque tour de la première roue, etc. Toutefois, le mécanisme pouvait inclure une "double avancée". Au moment d'effectuer la rotation du troisième rotor, le système pouvait pousser sur l'encoche du précédent rotor. Ainsi, à la fois le dernier rotor et le second rotor avançaient d'un cran. C'est ce fonctionnement qui fait varier ce mécanisme de celui d'un odomètre.
Le Réflecteur
Excepté les premiers modèles des machines Enigma, le dernier rotor était suivi d'un réflecteur. Le réflecteur connecte les sorties du dernier rotor (contacts plats) par pair. Ainsi, le courant arrivant dans le réflecteur va repartir dans le dernier rotor et reparcourir les rotors dans le sens inverse mais en empruntant un chemin différent.
Suivant les versions des machines, le réflecteur pouvait être inséré dans plusieurs positions ou pouvait encore subir le même mécanisme de rotation que les rotors.
La table de permutations
La table (ou tableau) de permutations ( ou connexion) avait pour objectif d'ajouter encore plus de complexité en passant par une dernière étape de substitution. La table, composé de 26 lettres, permet d'encoder les lettres deux à deux. Ainsi, si après l'étape des rotors, le courant se dirigeait vers A et que A était permuté à X, X s'allumerait. Cette étape, peu importante soit-elle, permettait d'ajouter de la complexité simplement.
Le nombre de permutations à établir était de 20 sur 26.
Fonctionnement en détails
Dans le détail :
1- La première étape correspond à la mise sous tension de la machine à l'aide de la batterie. Sans cela, impossible d'envoyer un signal via les interrupteurs.
2- Ensuite on presse une touche du clavier (dans notre exemple, c'est la touche A) pour envoyer le courant à la table de permutation.
3- Le courant est envoyé à la case A de la table de permutations. Il se trouve que A n'est permuté avec aucune lettre donc rien ne se produit.
4- Le courant se dirige ensuite vers le premier rotor.
5- Il continue son chemin dans les rotors suivants.
6- Il passe dans le réflecteur puis effectue un second passage dans les rotors (différent du premier passage).
7- La lettre chiffré est S. Le courant se dirige donc à nouveau vers la table des permutations, à la case S.
8- Celle-ci est permutée avec D, le signal passe donc dans la case D.
9- La lampe correspondante s'allume. Ici, la lampe D s'éclaire.
Notre lettre A chiffrée devient donc D. Une fois le signal passé dans le circuit, le rotor effectue sa rotation.
Principe de chiffrement
Le chiffrement de la machine Enigma est un chiffrement polyalphabétique. Contrairement à des chiffrements similaires comme Vigenère, il n'y a pas de clé. Chaque fois que l'on appuie sur une touche et que les rotors tournent, un nouvel alphabet de substitution est utilisé. Il y a 26 permutations possibles par rotor soit 26*26*26 = 17576 alphabets de substitution. De plus, l'ordre dans lequel ces alphabets sont utilisés dépend de la position de départ de chaque rotor, des rotors utilisés, et de l'ordre dans lequel ils sont installés dans la machine.
Le nombre de combinaisons possibles peut être calculé en tenant compte de la position des rotors, du nombre possible d'alphabets de substitution et des branchements du tableau de connexion. Sur les machines standards, on choisit 3 rotors parmi 5 soit possibilités. Le nombre d'alphabets de substitution, calculé précédemment, est de 17576. Enfin, on permute 20 lettres parmis 26 sur le tableau de connexion ce qui nous donne permutations possibles. Si l'on multiplie ces trois chiffres, on obtient combinaisons possibles au total. Ce qui est énorme pour l'époque, étant donné qu'il faudrait tester toutes les possibilités à la main, une par une, pour craquer un message en utilisant une attaque par brute force.
Mise en oeuvre
Le chiffrement et le déchiffrement d'un message sont effectués manuellement par une équipe de deux chiffreurs selon une procédure très précise.
Préparation de la machine
Avant de commencer le chiffrement à proprement dit du message, plusieurs réglages de la machine sont nécessaires. Ces réglages changent régulièrement de manière mensuelle, hebdomadaire ou quotidienne selon les réglages et les corps d'armées. Les instructions de réglages sont contenues dans des livres détenus par les chiffreurs. Les étapes à suivre sont les suivantes :
- Choix et positionnement des rotors dans le bon ordre, selon les instructions du jour. Par exemple le rotor I, puis le rotor IV puis le rotor II, notée I-IV-II dans le livre d'instructions.
- Positionnement de la bague des trois rotors, selon les instructions du jour. Par exemple la bague du premier rotor sur la position 06, celle du deuxième sur 20 et la dernière sur 24, notée FTX dans le livre d'instructions.
- Branchements sur le tableau de connexions, selon les instructions du jour. Par exemple, U avec A, P avec C, etc ..., notée UA-PC-... dans le livre d'instructions.
- Un des chiffreurs (appelons le Chiffreur 1) positionne alors les rotors sur les positions indiquées dans le livre d'instructions. Par exemple JCM.
- Chiffreur1 choisit alors une position aléatoire des rotors, mais ne modifie pas encore leur position pour l'instant. C'est la clé brute du message. Prenons BGZ pour l'exemple. Il tape alors deux fois la clé sur la machine (BGZBGZ).
- Le deuxième chiffreur note le résultat affiché par les voyant : c'est le clé chiffrée.
- Le premier chiffreur dispose alors les rotors selon la position qu'il a choisit au préalable. Le chiffrement du message peut commencer.
Envoi d'un message chiffré
Afin de chiffrer le message, le premier chiffreur tape les lettres du message une par une, et le deuxième chiffreur note le chiffré de chaque lettre (donné par la LED allumée).
Un message commence toujours par des indicateurs permettant d'identifier l’émetteur ainsi que la date et l'heure d'émission ainsi que le nombre de lettre du message. On trouve ensuite un indicateur de 5 lettres qui identifient le réseau Enigma et permet d'identifier le livre d'instructions utilisé pour le chiffrement (donc celui à utiliser pour le déchiffrement). Vient ensuite la clé chiffrée puis le corps du message.
Afin de renforcer la sécurité, les allemands codaient certains mots ou expressions et transposaient les coordonnées géographiques. Ainsi, même déchiffrés, certains messages n'avaient toujours aucun sens pour un non initié.
Les opérateurs envoient ensuite la message en morse au moyen d'un poste radio.
Réception et déchiffrement du message
Lorsque le destinataire reçoit le message depuis un poste radio il le note sur un bout de papier et le confie à un chiffreur. Pour déchiffrer, le chiffreur suit les mêmes étapes de préparations (1 à 4), selon les instructions du registre utilisé par l'émetteur. Il obtient alors la clé brute en tapant la clé chiffrée sur la machine. Il positionne alors les rotors selon les positions indiquées par la clé et déchiffre le message en tapant chaque lettre une à une et en notant le résultat.