« Utilisateur:Maxent Bernier » : différence entre les versions
| Ligne 27 : | Ligne 27 : | ||
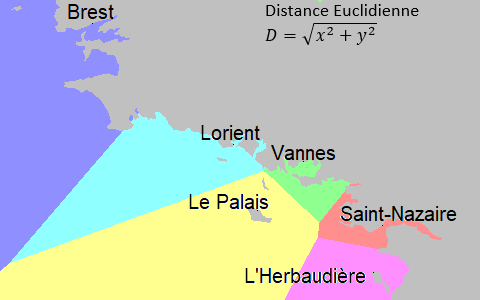
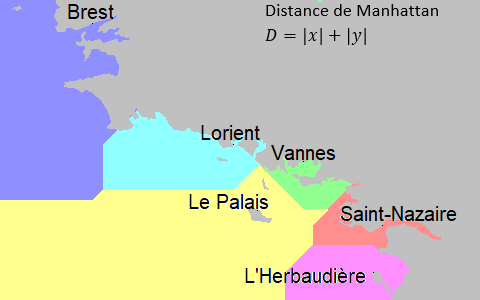
Le mathématicien attentif pourra remarquer que le segment séparant deux régions se trouve sur la médiatrice des ports des deux régions. Ici nous avons utilisé la distance Euclidienne, c'est-à-dire la longueur du segment donc deux points sont les extrémités. Cependant il en existe d'autres. Par exemple, si notre marin ne pouvait se déplacer que horizontalement et verticalement, on utilise alors la distance de Manhattan, qui donne un diagramme différent. |
Le mathématicien attentif pourra remarquer que le segment séparant deux régions se trouve sur la médiatrice des ports des deux régions. Ici nous avons utilisé la distance Euclidienne, c'est-à-dire la longueur du segment donc deux points sont les extrémités. Cependant il en existe d'autres. Par exemple, si notre marin ne pouvait se déplacer que horizontalement et verticalement, on utilise alors la distance de Manhattan, qui donne un diagramme différent. |
||
[[Fichier:VoronoiEuclidien.png]] |
|||
[[Fichier:VoronoiManhattan.png]] |
|||
Version du 4 mai 2021 à 11:54
Transformée en distance discrète, diagramme de Voronoi discret, axe médian et squelette
Tuteur : Jacques-Olivier LACHAUD
Etudiant : Maxent BERNIER
Qu'est-ce que Voronoi ?
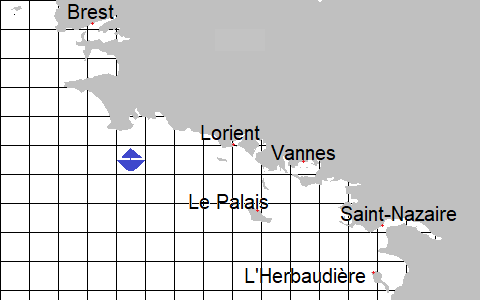
Imaginons un marin en mer. Une tempête s'annonce et il souhaite gagner le port le plus proche. Il dispose d'une carte et connait sa position.
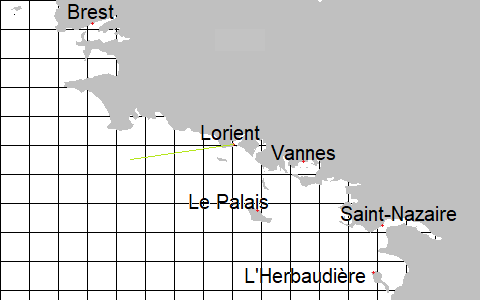
Ici, il est assez simple de voir que le port le plus proche est Lorient. On sait donc que si on se trouve sur cette case, Lorient est toujours le plus proche. Pour le représenter, on peut tracer une ligne ainsi.
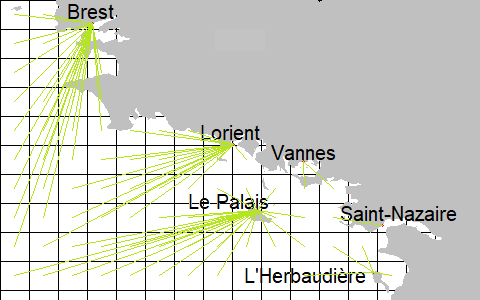
Si on utilise la même logique pour chacune des cases, on obtient ceci :
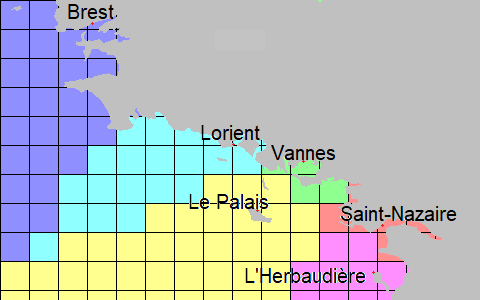
Les lignes n'étant pas très claires, on va les remplacer par des couleurs représentant chaque port.
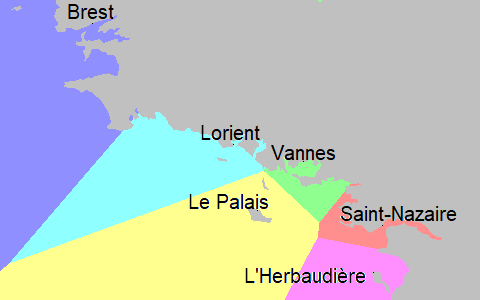
Nous venons de créer un diagramme de Voronoï; un plan divisé en région en fonction du port (germe) le plus proche. Ici les cases étant très grandes, il est difficile de savoir quelles cases sont dans quelle région. Voici la même carte en traitant chaque pixel de l'image.
Le mathématicien attentif pourra remarquer que le segment séparant deux régions se trouve sur la médiatrice des ports des deux régions. Ici nous avons utilisé la distance Euclidienne, c'est-à-dire la longueur du segment donc deux points sont les extrémités. Cependant il en existe d'autres. Par exemple, si notre marin ne pouvait se déplacer que horizontalement et verticalement, on utilise alors la distance de Manhattan, qui donne un diagramme différent.