Réductions de problèmes

Transformer un problème que l’on souhaite résoudre en une ou plusieurs instances d’un autre problème que l’on sait résoudre s’appelle, en complexité algorithmique, une réduction de problème. C’est le cas du problème, utilisé dans ce projet, de couverture exacte.
Dans le cadre de ce projet, les programmes ont été écrits en python et appelés sur Ubuntu afin d’utiliser le programme Dancing Links.

Problème de couverture exacte

Définition

Le problème de couverture exacte est un problème classique en informatique et utilisé dans la résolution de problèmes logiques tels que le sudoku, le pavage par polyominos, le problème des n reines, etc.
Le problème de couverture exacte consiste à choisir des ensembles qui vont pouvoir répondre à des contraintes. Cependant, chacune de ces contraintes doivent être répondus par un unique ensemble.
Par exemple, dans le jeu du sudoku, la contrainte est que chaque case doit être remplie tel que toutes les colonnes et lignes doivent contenir exactement un chiffre de chaque type (1, 2, 3, …).

Exemples

Exemple dans les ensembles :
Prenons un ensemble E = {a, b, c} et un ensemble S = {{a, b}, {a, b, c}, {c, b}, {c}} de parties de E.
Une couverture exacte de E est C, un sous-ensemble de S, tel que chaque élément de E est un élément d’exactement un des ensembles de C .
Ici, C = {{a, b}, {c}}. IMAGE (légende : « Exemple de problème de couverture exacte dans les ensembles »)

Exemple dans les matrices :
Le problème de couverture exacte peut également être représenté sous forme matricielle. Les colonnes correspondent aux contraintes à respecter et les lignes aux choix possibles pour former la couverture exacte. Chaque case de la matrice contient un 1, si la contrainte est respectée, ou un 0, sinon.
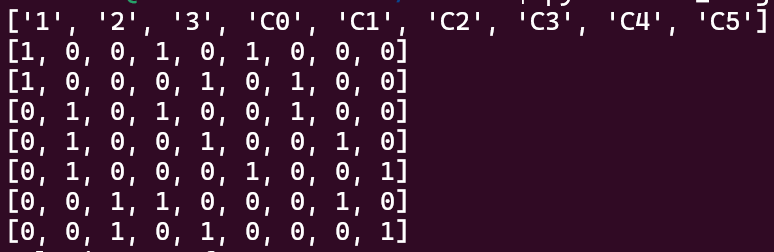
Soit E = {1, 2, 3, 4} et S = {F, G, H, I, J, K}. Le problème de couverture exacte est représentée par la matrice suivante :

	1	2	3	4
F	0	1	1	0
G	1	0	1	0
H	0	0	0	1
I	0	1	1	1
J	1	1	0	1
K	1	0	0	0

Une couverture exacte de ce problème est C = {F, H, K}:

	1	2	3	4
F	0	1	1	0
H	0	0	0	1
K	1	0	0	0

Problèmes réduits par couverture exacte

Suite de Langford

Une suite de Langford d'ordre 3

Problème

Une suite de Langford pour un entier k est une suite de 2k entiers constitué des entiers de 1 à k. Ces entiers sont placés les uns à la suite des autre de sorte qu’un entier i soit placé à i+1 place de l’autre entier i.

Passage par une matrice

Exemple de matrice pour une suite de Langford d'ordre 3

Pour résoudre les suites de Langford, on peut le réduire en instance de couverture exacte en utilisant une matrice représentant toutes les possibilités.
La matrice associée à une suite de Langford, pour un entier k, possède la structure suivante :

• Les k premières colonnes indiquent quel entier est traité ;
• Les colonnes suivantes représentent les positions (de 0 à 2*k) où placer chaque entier ;
• Chaque ligne désigne un placement possible pour deux entiers égaux.

Pour créer cette matrice, on va se baser sur la création d’une première ligne qui désigne les noms des colonnes et indique le nombre de colonnes total de la matrice.
Grâce à cette première ligne, le reste de la matrice va pouvoir être créée ligne par ligne. Créer une ligne consiste à mettre un 1 dans la colonne correspondante à l’entier que l’on veut placer et à mettre deux 1 dans les colonnes correspondant à un emplacement possible pour la paire de cet entier. La deuxième position se déduit de la première puisqu’elle est à i+1 place de celle-ci.
Pour le bon fonctionnement du passage de la matrice, créée en python, au programme suivant, il faut d’abord la formater sous forme de string et retirer les placements symétriques de l’entier 1 (par exemple) pour ne pas avoir le double de solutions attendues (les solutions + leur symétrique).

Fonctions d’appel de DLX et de traitement de sa sortie

Utilisation DLX

Afin de trouver une couverture exacte de cette matrice, nous allons utiliser le programme Dancing Links (DLX) qui prend en entrée l’ensemble des éléments d’une matrice qui sont à 1 et en sort les couvertures exactes.
Le programme python va être exécuté via Ubuntu avec les arguments nécessaires à son fonctionnement et à celui de DLX:

• Un entier indiquant l’ordre de la suite de Langford ;
• Un argument pour afficher les solutions voulues (m1, m1 t1, etc.).

Depuis le programme python, on peut appeler DLX en lui donnant ses arguments et récupérer sa sortie.

Solution à l'ordre 3

Solutions

Les solutions sont récupérées sous forme d'une longue chaîne de caractères, elles doivent donc être formatées pour les obtenir sous forme de suite de Langford.
Le problème des suites de Langford n’est pas forcément simples à résoudre, en particulier pour des grand nombre. Mais pour trouver ses solutions, on a écrit un programme python qui, algorithmiquement, n’est pas compliqué parce qu’il est réduit par couverture exacte, à l’aide de Dancing Links.

Problème de pavage avec les polyominos

Problème

Fichier:Bruh.png

Exemple de polyominos

Les polyominos sont des configurations formées de plusieurs carrés identiques. On retrouve les tétrominos (polyominos à quatre carrés) dans le jeu Tetris.
Un problème de pavage par les polyominos consiste à recouvrir exactement une surface prédéfinie par des polyominos.