Tables de hachage et dictionnaires

Les tables de hachages sont des tableaux dynamiques permettant de créer une association clé-valeur pour une retrouver rapidement une valeur. Les codes proposés ici pour les tables et fonctions de hachages sont écrits en langage Python. Les dictionnaires Python sont également basés sur le principe des tables de hachage et serviront d’outil de comparaison.

Définitions

• Table de hachage : tableau associatif permettant de créer une association clé-valeur. Chaque couple ou valeur se voit attribuer une position dans la table à l’aide d’un entier, appelé valeur de hachage, renvoyé par une fonction de hachage. Cette position dépend de la taille de la table et non de l’ordre d’arrivée. La recherche ou modification d’une valeur, la suppression ou l’ajout d’un couple s’effectuent à l’aide de la clé, elle apparaît donc de façon unique dans la table.
• Fonction de Hachage : fonction associant une valeur entière de taille prédéfinie à un entier, un flottant ou une chaine de caractères de taille non prédéfinie.

Fonction de Hachage

Première approche des fonctions de hachage

Une fonction de hachage prend en paramètre un élément ‘hachable’, c’est-à-dire un élément immuable, en python ce sont les chaines de caractères, un entier, un flottant ou encore un tuple. Le but est de transformer cet élément en un nombre entier de taille définie pour ensuite qu’il devienne un indice correspondant à une position dans la table de hachage.

Réduire des éléments de taille non définie en entier de taille définie risque de causer des collisions, c’est-à-dire qu’au moins deux éléments obtiennent le même résultat. Or selon le format des tables, ces éléments ne peuvent pas occuper la même position (2.3). Ce problème est inévitable lorsque les ajouts d’éléments ne sont pas prédictibles. Le mieux est donc de limiter le nombre de collisions. Pour cela, il faut bien construire la fonction de hachage.

Exemple d'une mauvaise fonction de hachage

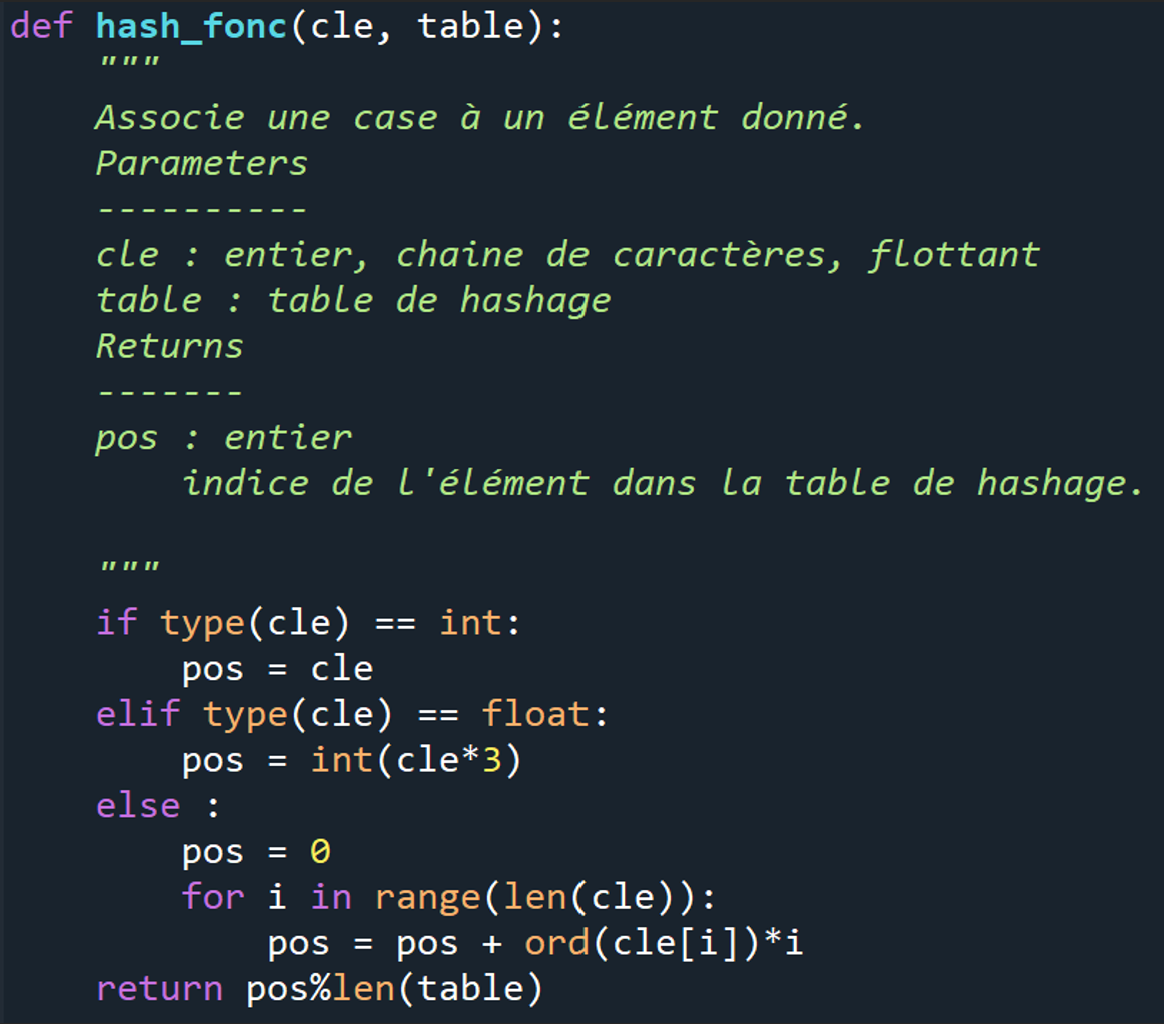
Par exemple la fonction ci-contre n’est pas une bonne fonction de hachage car :

• La table de hachage apparait dans la fonction, or la fonction de hachage doit en être indépendante.
• Le ‘else’ permet d’associer un entier à une chaine de caractère : l’indice est la somme de chaque caractère de la chaine transformée en son numéro ASCII puis multipliée par sa position dans la chaine. Ainsi, chaque premier caractère de chaine n’est pas pris en compte dans la somme (multiplication par 0) donc les chaines d’un caractère ont toutes pour indice 0 de la même façon, ‘mot’, ‘lot’, ‘got’ ont le même indice, etc…
• Pour ce qui est des entiers, tous les nombres entiers multiples de la taille de la table auront le même indice. La répartition des positions n’est pas suffisamment homogène.

Un autre exemple de fonction à éviter, est une fonction qui effectue une multiplication par un entier pair. Les cases occupées de la table se limiteraient alors aux indices pairs.

Ainsi, il est recommandé d’effectuer une multiplication par un grand nombre premier pour améliorer la répartition lors du modulo étant donné que les propriétés des nombres premiers sont utilisées. De la même façon, il est bien que le modulo final soit un nombre premier. Enfin, la réduction de l’indice à une position de la table se fera directement dans les méthodes de la table.

Différents types de fonctions

De nombreuses fonctions de hachage ont été imaginées pour répondre au mieux aux critères de répartition et de calcul.

Hachage multiplicatif

Le hachage multiplicatif consiste à prendre une clé m et la multiplier par une constante. Le modulo 1 conserve la partie fractionnaire seulement. Ce résultat est à nouveau multiplié par une puissance de 2 ce qui facilite les calculs pour l’ordinateur qui fonctionne avec des bits. En effet, une multiplication par n = 2p représente donc simplement un décalage p vers la droite. L’indice renvoyé est la partie entière de ce nombre.

Formule : $hash(m)=floor({n}\times {(({m}\times {c})mod1)})$ Avec m la clé, c une constante et n une puissance de 2.

Hachage de Fibonacci

Le hachage de Fibonacci est une variante du hachage multiplicatif. La constante c du hachage multiplicatif est à présent ${\dfrac {2^{t}}{8}}$ Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle frac{2^t}{{{lang|el|ϕ}}}}