« Surfaces polygonales et surfaces de subdivision » : différence entre les versions
| Ligne 31 : | Ligne 31 : | ||
to_vertex : <strong style="color:#7ED957">[<strong style="color:#38B6FF">1,0,2,1,0,2</strong>]</strong> |
to_vertex : <strong style="color:#7ED957">[<strong style="color:#38B6FF">1,0,2,1,0,2</strong>]</strong> |
||
face : <strong style="color:#7ED957">[<strong style="color:# |
face : <strong style="color:#7ED957">[<strong style="color:#ff5555">0,-1,0,-1,0,-1</strong>]</strong> |
||
Version du 11 mai 2024 à 12:37
Élève : Vetea STOLL
Tuteur : Jacques Olivier Lachaud
Définitions
Surface
Structure de données demie arêtes ailées
Description
Dans cette structure de données les arêtes (ex point A et B) sont décomposée en 2 demie arêtes (A vers B et B vers A) sont définies implicitement par un indice.
Chaque demie arête a une demie arête suivante (next) une demie arête opposée (opp) un point vers lequel la demie arête pointe (to_vertex) et l'indice de la face à laquelle la demie arête est associée (face), si il n'y a pas de face on mettra -1 par convention.
Pour accéder à ces paramètres on définie des listes de longueur n avec n nombre de demie arêtes pour chaque paramètre.
Les faces ont une demie arête associée de façon arbitraire (w_face) également pour les points (w_vertex).
On fera également des listes pour ces paramètres de longueur n avec n nombre de face et nombre de points.
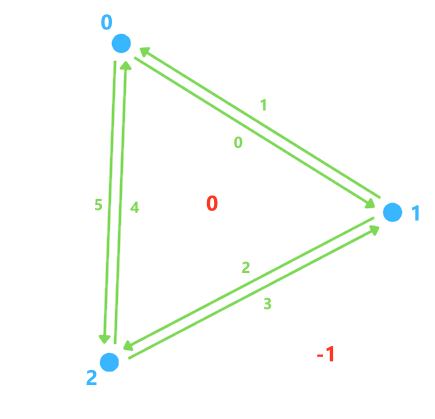
La structure de donnée d'un triangle ressemblera à ça :
next : [2,5,4,1,0,3]
opp : [1,0,3,2,5,4]
to_vertex : [1,0,2,1,0,2]
face : [0,-1,0,-1,0,-1]
w_face : [0]
w_vertex : [1,3,5]
Conversion
La structure de données qu'on a est définie par une liste de faces, chaque face étant une liste contenant les index des points associés.
Notre triangle ressemblerait alors à ça :
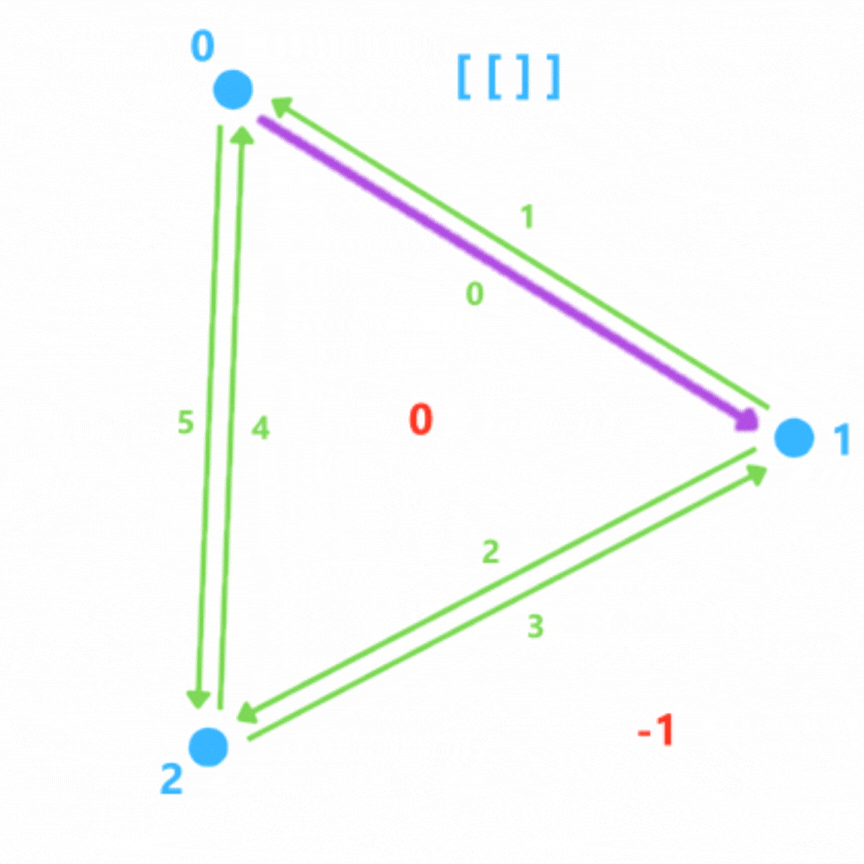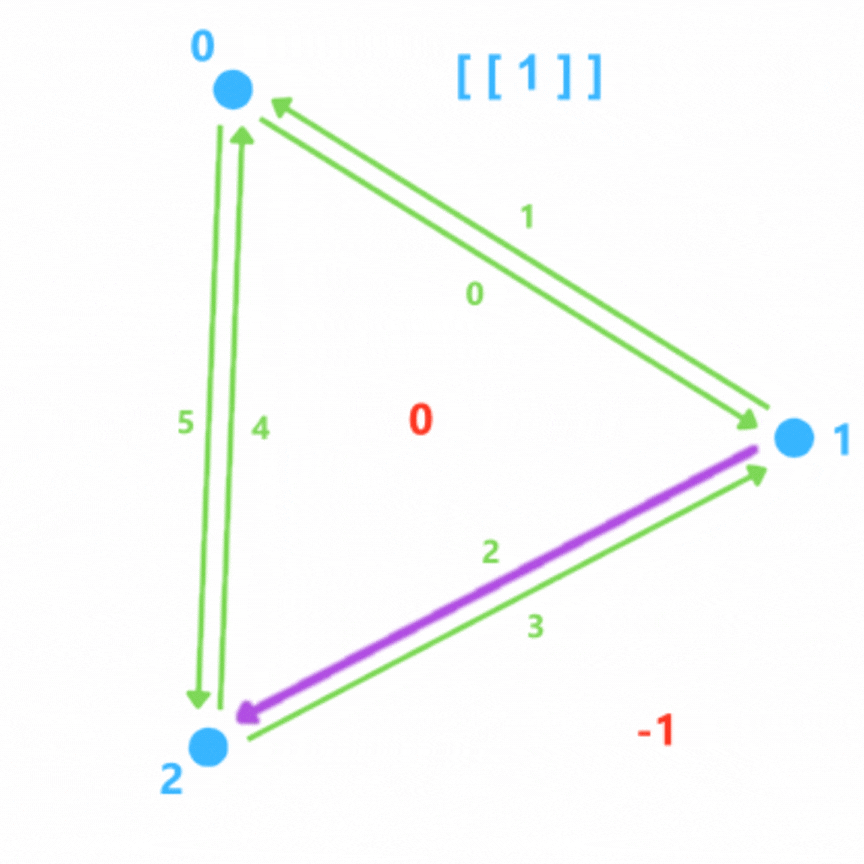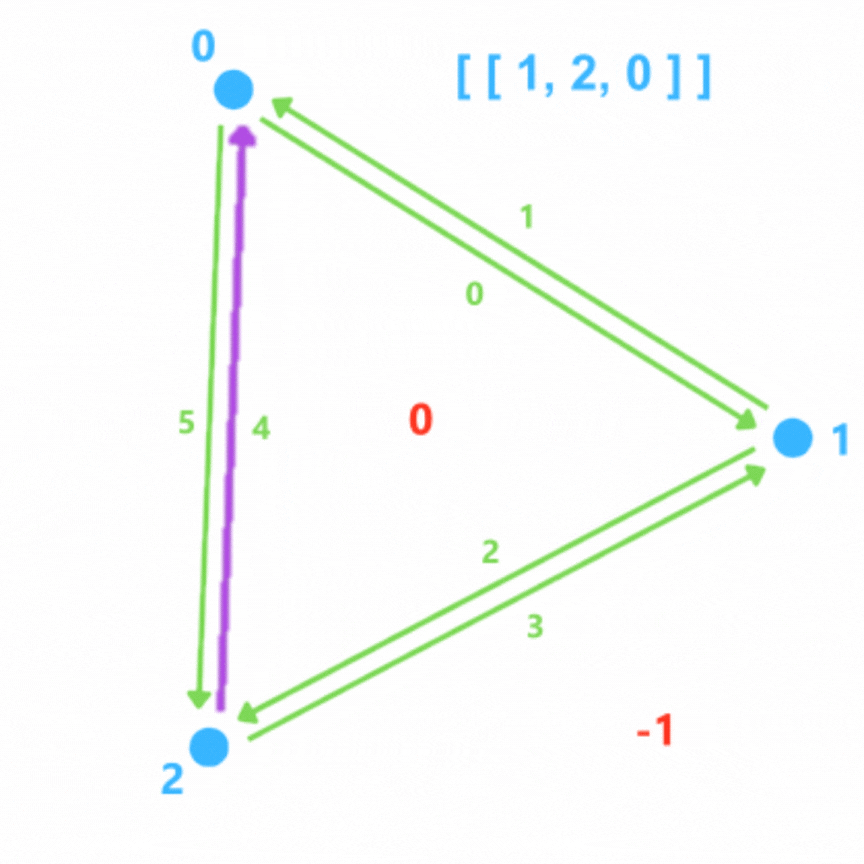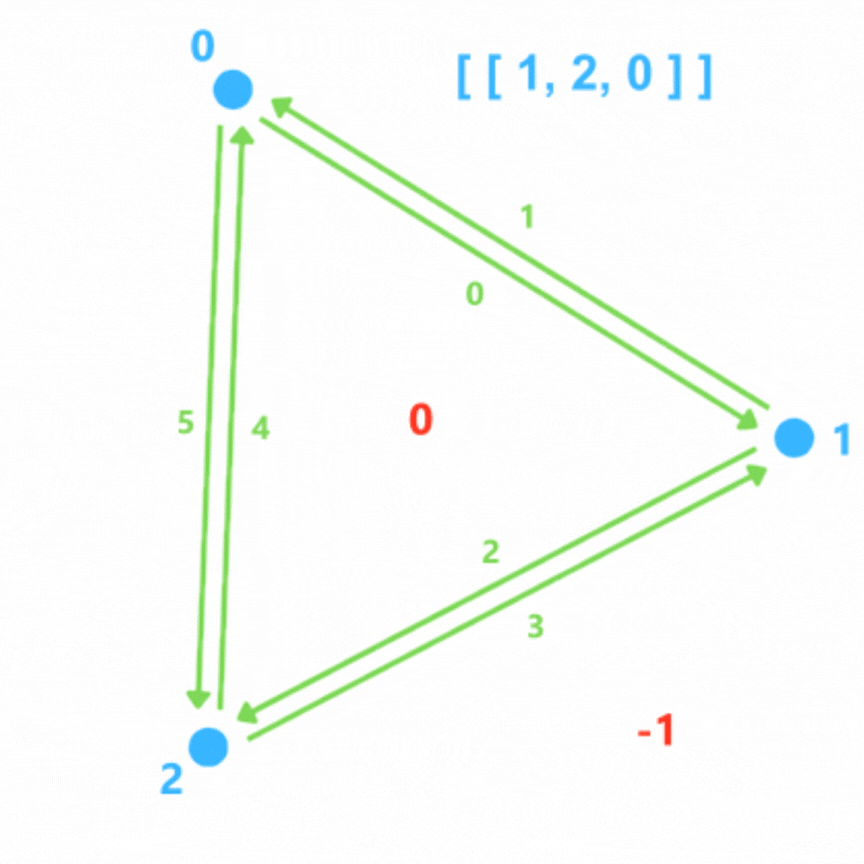
faces = [ [0,1,2] ]
On parcourt la liste des faces et on parcourt chaque face. On a donc des arêtes définies par pointA = faces[ i ] [ j ] et pointB = faces[ i ] [ (j+1) % len(faces[ i ]) ].
On peut alors définir une demie arête (pointA -> pointB) ainsi que son opposée (pointB -> pointA) en faisant attention attention qu'elle n'aie pas déjà été définie.
Pour définir des indices aux demies arêtes il suffit de garder en mémoire le nombre d'itérations qui ont eu lieu, qu'on va appeler n. Chaque demie arête aura l'indice 2n et chaque demie arête opposée aura l'indice 2n+1
Les listes sont alors un jeu d'enfant à remplir, excepté next, en particulier quand on définie les demies arêtes opposées car on ne sait pas à l'avance quel sera la demie arête suivante. On les définie alors par -1 temporairement.
Quand l'algorithme continue, si quand on veut définir une demie arête, on se rend compte qu'elle a déjà été créée, on update ses listes next et face. Mais il reste alors les demies arêtes du bord.
Après avoir executé cette première partie de la conversion, on s'occupe donc des next pour les demies arêtes opposées.
On commence par parcourir la liste des demies arêtes au bord (celles pour lesquelles la face associée est -1) et pour chaque demie arête, on prend l'opposée et tant que la demie arête n'est pas au bord, on prend l'opposée de la demie arête précédente (l'inverse de next).
Cette demie arête est donc la suivante de celle que l'on avait au départ.
Déconversion
La déconversion est un peu plus simple. On commence par parcourir w_face, et on rajoute le to_vertex de la demie arête dans une liste tant que la demie arête suivante n'est pas celle que l'on avait au départ.