« Génération et résolution de labyrinthes II » : différence entre les versions
| Ligne 31 : | Ligne 31 : | ||
En plaçant un point sur chaque cellule de notre labyrinthe, et en reliant deux cellules séparées par une porte, on peut dessiner un arbre comme ceci : |
En plaçant un point sur chaque cellule de notre labyrinthe, et en reliant deux cellules séparées par une porte, on peut dessiner un arbre comme ceci : |
||
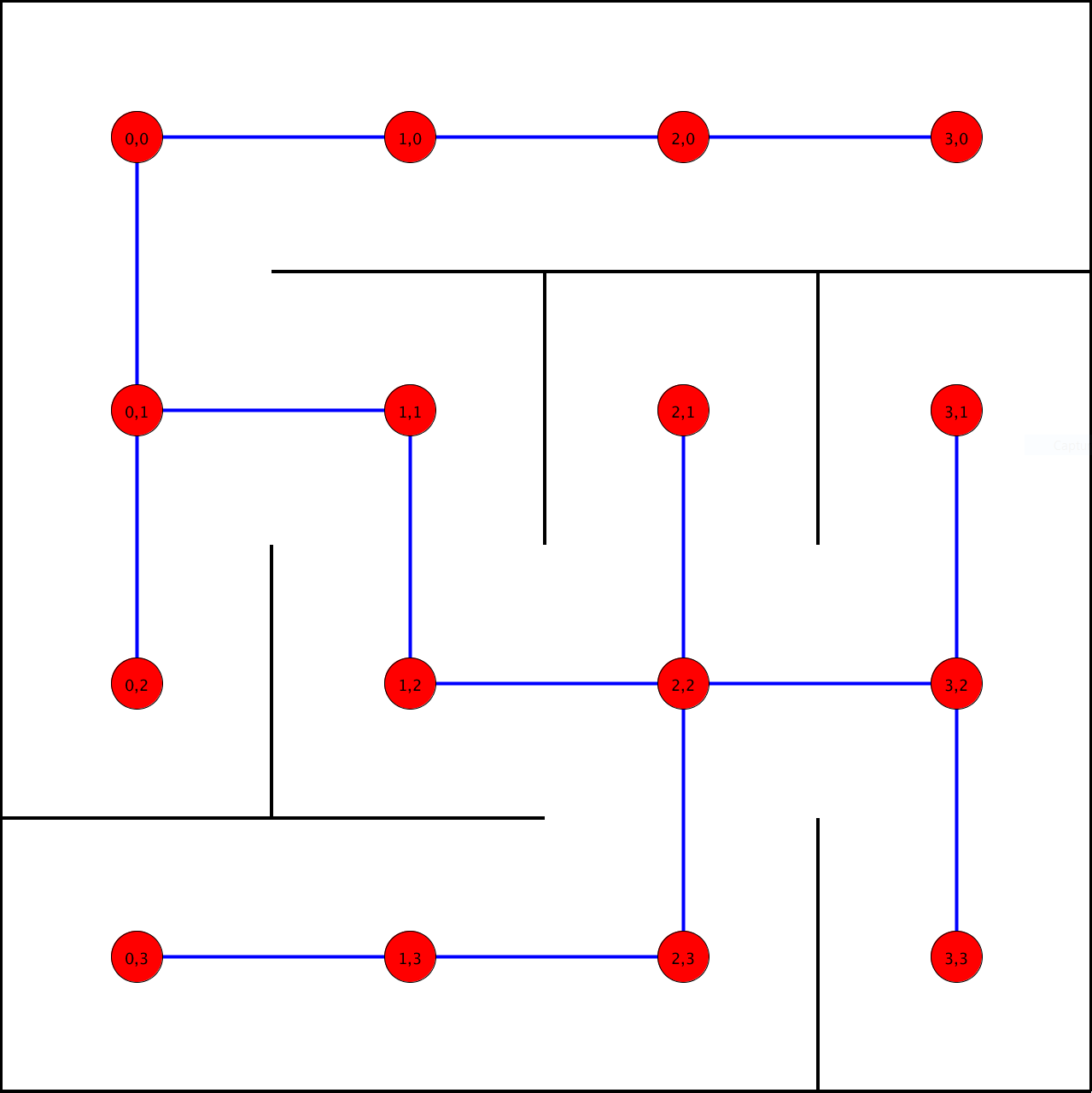
[[Fichier:labyrinthe_avec_arbre.png|vignette|centre|500px|Exemple de labyrinthe avec son arbre. |
[[Fichier:labyrinthe_avec_arbre.png|vignette|centre|500px|Exemple de labyrinthe avec son arbre. Pour plus de simplicité, on attribue à chaque nœud une position.|alt=Labyrinthe avec arbre]] |
||
== Génération == |
== Génération == |
||
Version du 16 mai 2019 à 14:20
bla bla blabla dsdsds
Définition
Propriétés d'un labyrinthe
Un labyrinthe est une grille de cellules reliées, ou non, entre elles.
Deux cellules sont reliées entre elles par une porte, ou séparées par un mur.
Tout labyrinthe a une entrée et une sortie, et quelle que soit l'entrée ou la sortie, le chemin entre ces deux cellules est unique.
Modélisation en graphe
En théorie des graphes, un graphe est un ensemble de points (ou nœuds ou sommets) reliés ensemble par des lignes (ou liens ou arêtes).
Un graphe peut être connexe (en un seul morceau) ou non connexe (en plusieurs morceaux).
Un graphe peut aussi être cyclique si les points sont reliés en formant une boucle ou acyclique.
Enfin, un graphe peut être orienté (si les arêtes sont à sens unique) ou non orienté.
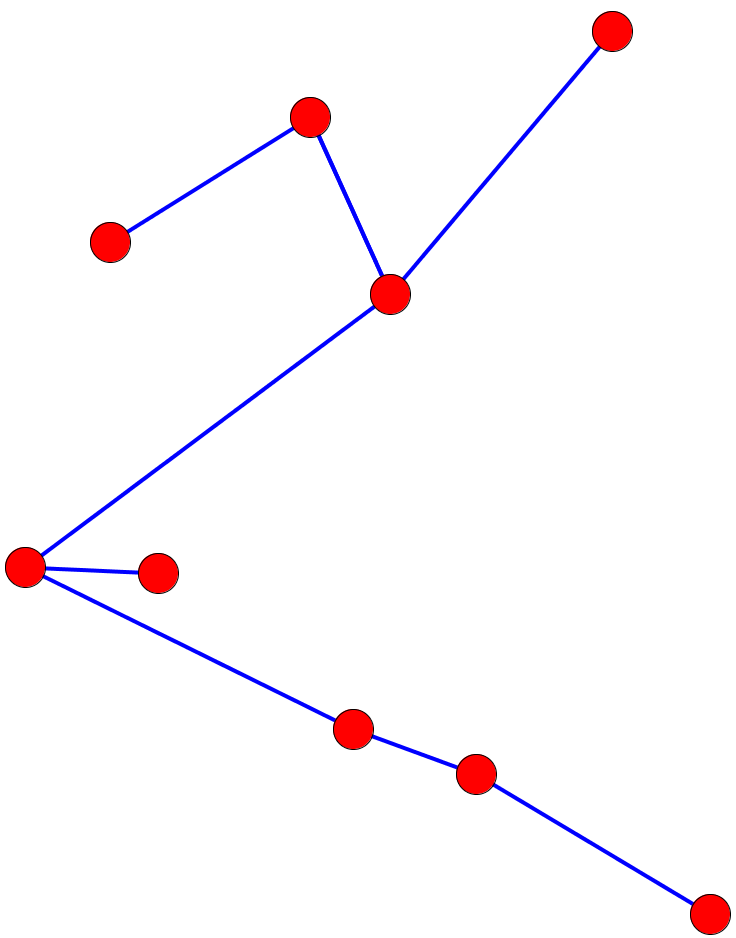
Un arbre est un graphe connexe, acyclique et non orienté.
En plaçant un point sur chaque cellule de notre labyrinthe, et en reliant deux cellules séparées par une porte, on peut dessiner un arbre comme ceci :
Génération
?
Exploration exhaustive
Recursive Backtracker
Kruskal
Kruskal
Prim
?
Résolution
?
Exploration exhaustive
Mur droit
Structures de données
Union-Find
Dijoint Set
Pile
Stack
File
Queue
Affichage
tkinter
Code
Lien google drive