Dilemme du prisonnier

Introduction

Le dilemme du prisonnier à été inventer en 1950 par Albert William Tucker et fait parti de la théorie des jeux qui est un domaine des mathématiques étudiant les interactions entre différents individus qui sont conscients ou non de ces interactions. Ils devront donc faire des choix dont ils sont conscients ou non lors de ces interactions.

Le dilemme du prisonnier

Les individus sont soumis dans le dilemme du prisonnier à une interaction où ils ont deux choix soit ils coopèrent avec l’autre individu soit ils le trahissent. Les individus sont récompensés selon la matrice des Paiements suivante :

L’intérêt de la configuration actuelle de la matrice des Paiements actuelle est que les individus ont un intérêt certain à trahir l’autre mais que la coopération est la meilleur option pour les deux individus. On représente l’intérêt à trahir par rapport à la coopération par la variable B qui dans notre exemple est égale à 1,85.

Afin de simplifier notre modèle nous ne considérerons que deux comportements possibles qui sont :

-Le Croyant qui coopérera systématiquement

-Le Traître qui trahira systématiquement

Spatialisation du Dilemme du prisonnier

Nous spatialisons le dilemme du prisonnier afin d’expliquer en partie des observations dans le vivant où les êtres vivants coopèrent entre eux alors qu’ils ont tout à y gagner en ne le faisant pas. Pour étayer nos propos on propose la citation suivante :« The prisoners’ Dilemma is an interesting metaphor for the fundamental biological problem of how cooperative behaviour may evolve and be maintained »(Nowak, M.A. et May, R.M. 1992. Evolutionary games and spatial chaos). En spatialisant le dilemme du prisonnier nous pouvons observer l’évolution des pratiques dans des situations variées. Il est à noter que nous pouvons aussi établir des liens entre les domaines de l’économie et de la sociologie notamment.

Les prisonniers sont au voisinage de Moore (8 voisins) de tel sorte à ce que dans l’espace les voisins d’un prisonnier lambda soient disposés de la manière suivante :

1 2 3

4 P 5

6 7 8

L’espace dans lequel ils évoluent est un espace toroïdale (bordures ouvertes) en forme de carré de dimension n*n. On peut aussi le représenter comme une matrice carré avec les bordures qui communiquent entre elles.

À Chaque tour les prisonniers vont jouer au dilemme du prisonnier avec chacun de leurs voisins. Ils obtiendront un score conformément à leurs choix et à la matrice des Paiements. Puis chacun leur tour mettre à jour leur stratégie en fonction du score des voisins.

Afin de pouvoir visualiser l'évolution de notre espace nous avons créer un programme en Java afin de profiter des aspects suivant de Java:

Le premier est la programmation objet, cela nous permet de diviser la complexité de notre programme dans plusieurs objets interagissants entre eux. Nous pouvons aussi créer des abstractions d'objets qui nous permettent d'avoir des objets qui ont des comportements différents les uns des autres mais ayants tous des points communs ce qui permet de les manipulés plus facilement.

Le second est la bibliothèque Abstract Windows Toolkit (ou AWT pour faire plus court). Qui nous permet de faire sans trop de problèmes une fenêtre personnalisable qui affiche des composants grapihques. Ces composants étant eux mêmes variées, on utilisera surtout les propriétés du composant Canvas dans ce programme. Grâce à l’héritage permis par la programmation objet nous pouvons créer nos propres composants graphiques pour afficher nos résultats.

Notre programme crée donc une fenêtre qui affiche les prisonniers en fonction de leur stratégie actuelle et de leur dernière stratégie.Le code couleur est le suivant :

-en rouge les Traîtres qui l’ont été pendant 2 tours consécutifs

-en jaune les Croyants qui sont devenus Traîtres

-en vert les Traîtres devenus Croyants

-en bleu les Croyants qui l’ont été pendant 2 tours consécutifs

Une expérience intéressante

On propose dans cette partie de commencer à étudier un cas en particulier. Dans cette première expérience nous fixons B à 1,85 et plaçons un traître au milieu de croyants dans une grille de 301 par 301. Nous pensons que cette configuration donnera des résultats intéressants car B n'est pas assez grand pour permettre une domination complète des Traîtres ou pas assez petit pour permettre une domination complète des Croyants.

Après quelques tours de la simulation nous observons l'image suivante:

Nous pouvons voir grâce à la bordure verte que le carré de traîtres au centre de l'image est en train de rétrécir alors que dans les coins des îlots de traîtres apparaissent comme nous le montre la grand quantité de jaune.

Nous passons sous silence quelques tours pour arriver à la situation suivante:

Nous pouvons voir à présent que les comportements dans la simulation varient beaucoup comme témoignent l'abondance de prisonniers affichés en jaune et en vert.

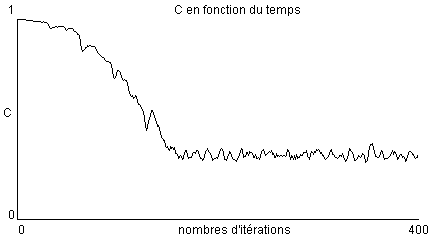
Lors du déroulé de cette simulation nous avons pus récolter C qui est le rapport entre le nombre de croyants dans la matrice sur le nombre de prisonniers au total. Cette variable nous permettra de visualiser l'évolution du nombre de croyants dans la simulation rapidement. Nous allons maintenant montrer son évolution au court du temps dans la simulation.

Nous pouvons ainsi observer sur le graphique que C semble tendre vers environ 0.3 montrant de ce fait que la simulation est dominé par les traîtres mais que les croyants résistent tout de même.

Automatisation des expériences

Nous avons pus observer une simulation particulière mais nous devons maintenant pouvoir faire des observations autres que visuelles car nous n’avons pas le temps de le faire pour toutes les expériences permisses par notre modèle. On n’as alors décidé donc de créer un objet dans le programme pour extraire les données des expériences et nous les résumées. Nous ne montrerons toutefois que les expériences que l’on juge intéressantes.

Nous voulons tout d'abord mesurer l'influence de B sur l'évolution d'une répartition aléatoire. Pour cela nous fixerons les paramètres suivants pour chaque simulation. Dans chaque simulation on aura systématiquement 10% de traîtres répartis aléatoirement parmi 90% de croyants. La dimension des matrices sera de 200*200.